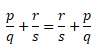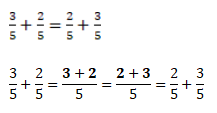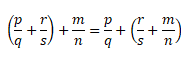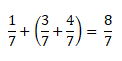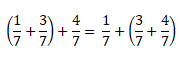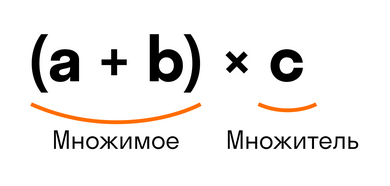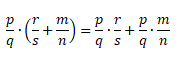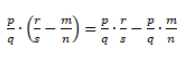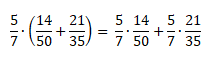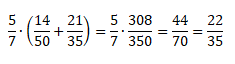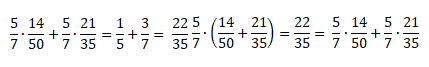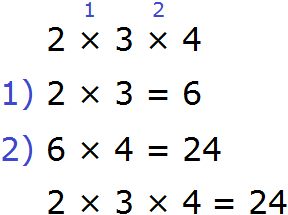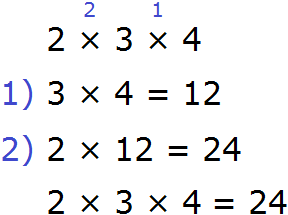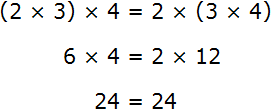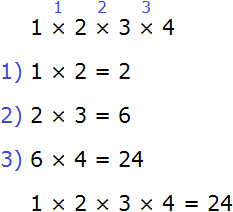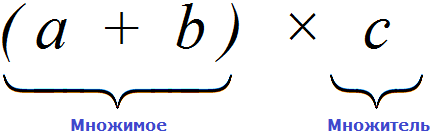какие законы есть в математике
Законы математики
Переместительный закон сложения
Начнем изучать основные законы математики со сложения натуральных чисел.
Переместительный закон сложения
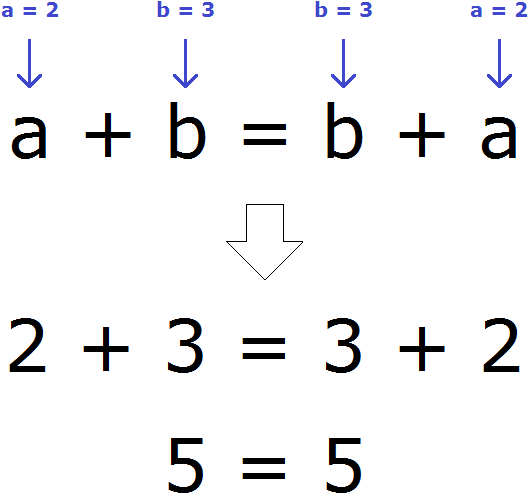
От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так:
m + n = n + m
Переместительный закон сложения работает для любых чисел.
Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.
Приведем пример с весами, которые используют продавцы в магазинах.
Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.
При этом неважно, как будут лежать конфеты, в каком порядке. Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.
Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:
Формула переместительного закона для обыкновенных дробей:
Чтобы сложить две дроби нужно сложить числители, а знаменатель оставить прежним. Вот так:
Сочетательный закон сложения
Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.
Сочетательный закон сложения: два способа
Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.
Рассмотрим сумму из трех слагаемых:
Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:
Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:
В обоих случаях получается один и тот же результат — что и требовалось доказать.
Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:
Отразим сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Формула сочетательного закона для обыкновенных дробей:
Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.
Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.
Значит, сочетательный закон справедлив и для обыкновенных дробей.
Переместительный закон умножения
С каждым новым правилом решать задачки по математике все интереснее.
Переместительный закон умножения
От перемены мест множителей произведение не меняется. То есть, если множимое и множитель поменять местами — их произведение никак не изменится.
Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:
В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.
Переместительный закон умножения с помощью переменных выглядит так:
a * b = b * a
Сочетательный закон умножения
Рассмотрим еще один полезный закон в математике.
Сочетательный закон умножения
Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий.
Другими словами, умножайте числа в любом порядке — как вам больше нравится.
Это выражение можно вычислить в любом порядке. Давайте сначала перемножим числа 2 и 3, а полученный результат умножим на 4:
А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:
Тот же ответ! Значит между выражениями (2 * 3) * 4 и 2 * (3 * 4) можно поставить знак равенства, так как они равны одному значению.
Для любых натуральных чисел a, b и c верно равенство:
a * b * с = (a * b) * с = a * (b * с)
Пример
Вычислить: 5 * 6 * 7 * 8.
Это выражение можно вычислять в любом порядке. Вычислим слева направо:
Распределительный закон умножения
Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:
Распределительный закон умножения
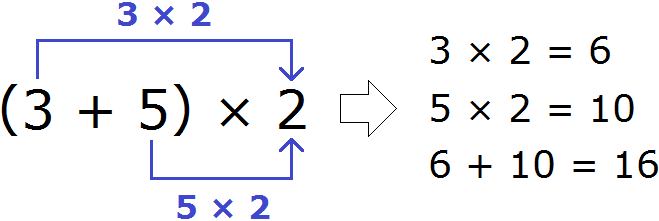
То есть при помощи распределительного закона умножения можно умножить сумму на число и число на сумму. Проверим на примере:
Сначала выполним действие в скобках:
В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:
Отразим распределительный закон умножения с помощью переменных:
(a + b) * c = a * c + b * c
Выражение в скобках (a + b) — это множимое. Тогда переменная с — множитель, так как они соединены знаком умножения.
Из переместительного закона умножения мы знаем, что от перемены мест множимого и множителя произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c * (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для такого умножения можно применять распределительный закон умножения. Переменную c можно умножить на каждое слагаемое в скобках:
c * (a + b) = c * a + c * b
Пример 1
Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:
5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25
Пример 2
Найти значение выражения 2 * (5 + 2).
Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:
2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14
Если в скобках не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. А после из полученного первого числа вычесть второе число.
Пример 3
Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:
4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16
Распределительный закон умножения для суммы обыкновенных дробей:
Распределительный закон умножения для разности обыкновенных дробей:
Проверим справедливость этого закона:
Посчитаем, чему равна левая часть равенства.
Теперь посчитаем, чему равна правая часть равенства.
Так мы доказали справедливость распределительного закона.
Задания для самопроверки
Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать 🙂
Задание 1. Найти значение выражения: 8 * (1 + 6).
Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).
Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).
Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).
Задание 5. Применить распределительный закон умножения: 13 * (3 + 8) + 5 * (4 + 2)
Задание 6. Какое из действий (умножение, деление, сложение или вычитание) нужно выполнить последним ((20 − 1) * 12 + 30) : 3?
Задание 7. В смартфоне 32 гб памяти. Какое количество приложений можно установить, если одно занимает 1,2 гб?
Задание 8. Верно ли равенство: 8 * 5 = 49?
Законы математики
В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.
У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем случае приводит к тому, что падают самолёты, зависают компьютеры, улетают крыши домов от сильного ветра, снижается качество связи и тому подобные нехорошие явления.
Законы математики состоят из простых свойств. Эти свойства нам знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.
В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.
Переместительный закон сложения
Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:
Если положить на одну чашу весов 10 килограмм яблок и на другую чашу так же положить 10 килограмм яблок, то весы выровнятся, и не важно, что яблоки в пакетах лежат вразброс. Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.
Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:
Полагаем что, вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:
Сочетательный закон сложения
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.
Рассмотрим сумму из трёх слагаемых:
Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Видно, что в обоих случаях получается один и тот же результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(2 + 3) + 5 = 2 + (3 + 5)
Запишем сочетательный закон сложения с помощью переменных:
Переместительный закон умножения
Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.
В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 × 2 = 2 × 5
Запишем переместительный закон умножения с помощью переменных:
Сочетательный закон умножения
Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
Рассмотрим следующее выражение:
Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:
Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2
Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
Запишем сочетательный закон умножения с помощью переменных:
a × b × с = (a × b) × с = a × (b × с)
Пример 2. Найти значение выражения 1 × 2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число или число на сумму.
Рассмотрим следующее выражение:
Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:
В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:
8 × 2 = 16
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:
Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:
(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16
(3 + 5) × 2 = 6 + 10 = 16
Теперь запишем распределительный закон умножения с помощью переменных:
(a + b) × c = a × c + b × c
Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.
Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×
Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.
c × (a + b) = c × a + c × b
Пример 2. Найти значение выражения 5 × (3 + 2)
Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:
5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25
Пример 3. Найти значение выражения 6 × (5 + 2)
Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:
6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42
Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.
Пример 4. Найти значение выражения 5 × (6 − 2)
Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20
Пример 5. Найти значение выражения 7 × (3 − 2)
Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
Законы арифметических действий
Нам известны следующие законы сложения и умножения:
1. от перемены мест слагаемых сумма не меняется:
Это переместительный закон сложения.
2. Значение суммы не зависит от того, как сгруппированы слагаемые, т. е. чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое:
Это сочетательный закон сложения.
3. От перемены мест множителей произведение не меняется:
Это переместительный закон умножения.
4. Значение произведения не зависит от того, как сгруппированы множители, т. е., чтобы произведение двух множителей умножить на третий множитель, можно первый множитель умножить на произведение второго и третьего множителей.
Это сочетательный закон умножения.
5. Чтобы сумму умножить на число, можно умножить на это число каждое из слагаемых, а затем сложить полученные произведения:
Это распределительный закон умножения относительно сложения.
Применяя законы сложения и умножения, можно упростить вычисления:
В этих примерах использовался сочетательный закон сложения и умножения.
Пример #1.
Вычисли, меняя множители местами и объединяя их в группы:
Множители можно объединять в группы:
9 ⋅ 2 ⋅ 5 = 9 ⋅ (2 ⋅ 5) = 9 ⋅ 10 = 90.
Любое чётное число выгодно объединять с 5, т. к. произведение с ним даёт полные десятки.
Если множители не менять местами и не объединять, то получить результат будет сложнее, но тоже можно:
2 ⋅ 9 ⋅ 5 = 18 ⋅ 5 = 90.
Выполни умножение 44 ⋅ 2 постепенно.
44 ⋅ 2 = (40 + 4) ⋅ 2 = 40 ⋅ 2 + 4 ⋅ 2 = 80 + 8 = 88.
Обрати внимание, что каждое слагаемое в скобках умножается на число 2 отдельно, и полученные произведения потом складываются.
Вычисли устно: 67 + 21 + 33.
Данное равенство: 9 ⋅ 5 = 48 —
верно или ошибочно?
Какое из действий (умножение, деление, сложение или вычитание) нужно выполнить последним, определяя значение выражения ((27 − 0) ⋅ 14 + 79) : 2?
Сумма чисел 3338 + 2744 ближе всего к числу:
В автобусе 25 мест(-а). Какое наименьшее число автобусов необходимо, чтобы 182 чел. увезти в аэропорт?
Оставшимся 7 чел. нужен ещё один автобус.
Поэтому необходимое число автобусов 7+1 = 8.
Проверка: 25⋅7 + 7 = 175 + 7 = 182.
В конце рабочего дня 7 гномов (A, B, C, D, E, F и G) в алфавитном порядке собрались у лифта, чтобы подняться на поверхность земли.
К сожалению, одновременно все гномы не могут подняться на лифте, т. к. за раз лифт может поднять груз не больше, чем 475 кг.
Некоторые гномы не знают свой вес, однако известен общий вес некоторых гномов. A + G = 356 кг, B + F = 408 кг, C + D + E = 464 кг.
Свойства сложения и вычитания
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
При этом саму запись (2 + 5) можно тоже назвать суммой.
Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
Свойства вычитания
Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.
Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.
Уменьшаемое — это число, из которого вычитают.
Вычитаемое — это число, которое вычитают.
Разность — это число, которое получается в результате вычитания.