какие жидкости обладают сверхтекучестью
Как правильно плавать в сверхтекучей жидкости
Движение при полном отсутствии вязкости проявляется во многих впечатляющих эффектах: сверхтекучий гелий легко протекает через самые узкие щели и трещины, способен бесконечно течь по кругу (**) и вытекать из сосуда через тончайшую жидкую пленку, налипшую на его стенки. Все эти явления – примеры крупномасштабных квантовых эффектов.
В недавней теоретической статье был рассмотрен вопрос: можно ли плавать в сверхтекучей жидкости? Иными словами, может ли гипотетический пловец, двигая руками и ногами, создавать силу тяги, позволяющую ему разгоняться или замедляться, не задействуя силы вязкого трения?
Осознать нетривиальность ответа на этот вопрос можно, рассматривая поведение нормальной и сверхтекучей жидкостей при взаимодействии с телами. Как показано на рисунке, нормальную жидкость можно заставить двигаться, как толкая ее поверхностью твердого тела, так и увлекая ее за собой за счет сил вязкого трения. В сверхтекучей жидкости последнее не получится: трение в ней отсутствует, и ее можно только толкать, что, как мы увидим, делает невозможным некоторые способы плавания.
Для анализа общих принципов физических явлений принято рассматривать простые модели «сферических коней в вакууме». Обсуждаемая статья не является исключением: в ней были рассмотрены двухтельный и трехтельный модельные «пловцы», представляющие собой два и три эллипсоида, соединенных «суставами». Пловцы могут двигать своими эллипсоидами, сгибая и разгибая суставы. Если у пловца получится отталкиваться от окружающей жидкости, он создаст силу тяги и начнет двигаться.
Двухтельный пловец похож на двустворчатого моллюска и может пытаться плыть, периодически изменяя угол между своими эллипсоидами подобно машущей крыльями бабочке. Однако расчеты показывают, что плыть у него не получится: при взмахах пловец перемещается вперед и назад, но в среднем остается на месте (здесь можно посмотреть видео его незамысловатых движений).
Наверху: профиль плотности сверхтекучей жидкости в разные моменты времени. Синие участки, откуда жидкость выталкивается – это эллипсоиды двухтельного пловца.
Внизу: координата пловца как функция времени.
Можно провести параллели между этим результатам и теоремой Пёрселла о морском гребешке (Purcell’s scallop theorem). Эта важная теорема теории плавания гласит, что двустворчатый моллюск, медленно открывающий и закрывающий свою раковину в вязкой жидкости, не будет никуда плыть, коль скоро его движения будут обратимы во времени. Последнее означает, что периодические открывания и закрывания створок раковины не меняют свой вид при запуске времени в обратном направлении (можно представить себе видеоролик, выглядящий просмотре задом наперед точно так же, как при нормальном воспроизведении). В нашем случае жидкость не имеет вязкости, и работает не сама теорема Пёрселла, а ее аналог для сверхтекучей жидкости.
Рисунок из доклада Эдварда Пёрселла (лауреата Нобелевской премии по физике в 1952 году).
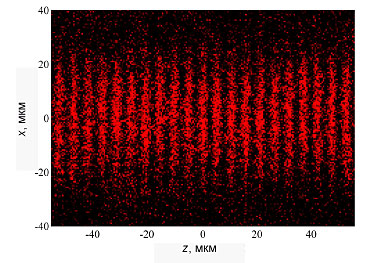
Можно попробовать и другой тип движения пловца, когда его створки смыкаются и раздвигаются не только в правом направлении, а попеременно в двух направлениях. Такие симметричные движения похожи на взмахи крыльев бабочки. Расчеты показывают, что при этом возбуждается много квантованных вихрей (они видны на рисунке как маленькие кружочки), но, в целом, плавание не очень эффективно. Причина в том, что возбуждается примерно одинаковое количество вихрей, движущихся как вправо, так и влево, и уносимые ими импульсы в значительной мере компенсируют друг друга (видео).
Рассмотрим теперь трехтельного пловца. Перед двухтельным у него есть важное преимущество: он может извиваться, совершая змеевидные движения, которые не переходят сами в себя при обращении времени. А значит, теорема Пёрселла к нему неприменима, и он должен плыть даже при медленных движениях. Приведенные на рисунке расчеты подтверждают эту догадку: при извивающихся движениях пловец уверенно продвигается по горизонтали, при этом немного смещаясь и по вертикали (видео).
Наверху: профиль плотности сверхтекучей жидкости в разные моменты времени. Синие участки, откуда жидкость выталкивается – это эллипсоиды трехтельного пловца.
Внизу: горизонтальная (X) и вертикальная (Y) координаты пловца как функции времени.
Какое применение можно найти полученным результатам? Казалось бы, задача о плавании в сверхтекучей жидкости не особо актуальна на практике, но есть одна область, где она может быть полезной. В последнее время активно развиваются эксперименты с бозе-конденсацией и сверхтекучестью ультрахолодных атомных газов, с которыми связывают большие планы по созданию квантовых симуляторов, квантовых компьютеров и экспериментальному моделированию экзотических состояний материи. В таких системах можно создавать сгустки сверхтекучего газа одного вида, погруженные в сверхтекучий газ другого вида. Если мы сможем деформировать сгусток так, как нам нужно (а это можно делать с помощью лазерных лучей), то можно будет заставить этот сгусток плыть, отталкиваясь от окружающего газа. На рисунке показаны расчеты, демонстрирующие такую возможность: когда изменения формы сгустка не являются обратимыми во времени, ему действительно удается двигаться (видео).
Итак, мы видим, что плавать в сверхтекучей жидкости нужно с умом: теорема Пёрселла гарантирует, что мы не сможем плыть, если наши движения руками и ногами будут совпадать с самими собой при проигрывании в обратном направлении. Чтобы начать перемещаться, нам нужно будет либо двигаться быстрее звука (что проблематично), либо извиваться подобно змее, нарушив обратимость движений во времени. Эти выводы хорошо знакомы плавающим в вязкой жидкости микроорганизмам: для того, чтобы обойти теорему Пёрселла, им приходится использовать спирально вращающиеся жгутики, являющиеся аналогами рассмотренного здесь трехтельного пловца.
По материалам статьи:
Hiroki Saito, Can We Swim in Superfluids?: Numerical Demonstration of Self-Propulsion in a Bose–Einstein Condensate, Journal of the Physical Society of Japan 84, 114001 (2015).
(*) На самом деле, это не совсем так: любая реальная сверхтекучая жидкость может быть представлена как совокупность «нормальной» и сверхтекучей компонент (двухжидкостная модель), и нормальная компонента будет по-прежнему замедлять движущееся тело. Однако это не мешает сверхтекучей компоненте двигаться полностью без трения.
(**) На практике круговой поток сверхтекучего гелия может затухать, но не из-за вязкости, а за счет квантовомеханического процесса – проскальзывания квантованных вихрей. В экспериментах не наблюдалось никакого заметного затухания в течение 18 часов.
(***) Возникающие в сверхтекучей жидкости вихри – это не просто вихри наподобие маленьких торнадо, а квантованные топологические возбуждения. В отличие от обычных вихрей, они не могут просто исчезнуть за счет постепенного затухания потока.
Квантовая жидкость и сверхтекучесть
Природа квантовой жидкости
Вещество переходит в состояние квантовой жидкости при очень низкой температуре, вблизи абсолютного нуля. Как следует из классической физики, при такой температуре атомы должны прекратить свое движение, образуя тем самым кристалл. Однако, в силу квантовых эффектов некоторые вещества с небольшой атомной массой и с высокой нулевой энергией (минимальная энергия системы) способны оставаться жидкостями.
Волны де Бройля – один из параметров, возникающий из математических глубин квантовой механики, который определяет плотность вероятности нахождения частицы в выбранном объеме конфигурационного пространства (пространство всех возможных значений всех параметров частицы). Чтобы заметить проявление квантовых эффектов в жидкости, требуется, чтобы длина волны де Бройля, вычисленная по энергии теплового движения частиц, была близка к значению расстояния между этими частицами. К примеру, для гелия подобное отношение будет возникать при температуре всего 2-3 К.
Зависимость состояния гелия от давления (ось ординат) и температуры (ось абсцисс)
Как уже говорилось ранее, вещества с высокой нулевой энергией способны становиться квантовыми жидкостями при низких температурах. Высокая нулевая энергия подразумевает наличие колебаний частиц даже при сверхнизких температурах. Если же амплитуда этих колебаний близка к среднему расстоянию между частицами вещества, то оно сохранит свою жидкую форму.
В зависимости от частиц, составляющих жидкость, она может быть бозонной (состоять из бозонов) и фермионной (состоять из фермионов).
Сверхтекучесть и другие свойства
Бозонные квантовые жидкости способны протекать через узкие капилляры или щели без какого-либо трения, это свойство называется сверхтекучестью. Примечательно, что подобное явление наблюдается не только у квантовых жидкостей, но и в некоторых бозе-конденсатах и даже в твердом гелии.
Материалы по теме
Нейтронные звезды
Сверхтекучесть объясняется следующим образом. Как известно, из квантовой механики следует, что бозоны способны находиться в одном состоянии. Тогда при низкой температуре, когда скорость частиц относительно невысокая, бозонам более энергетически выгодно сливаться в одно состояние, нежели взаимодействовать со стенками сосуда, то есть переходить в иное состояние, при котором возникает трение.
Сверхтекучесть была экспериментально достигнута жидкостями таких веществ как гелий-II (2,172 К), гелий-3, гелий-4 и водород (0,15 К). Вероятнее всего в недрах нейтронных звезд вещество находится в сверхтекучем состоянии.
В отличие от бозе-жидкостей, обладающих сверхтекучестью, фермионные квантовые жидкости с понижением температуры все менее способны пропускать звук, который, как известно, передается посредством колебаний частиц.
Частицы, составляющие сверхтекучие жидкости обычно представляются в виде конденсата Бозе — Эйнштейна.
Сверхтекучесть
Проживая практически в одних и тех же условиях на протяжении своей жизни, человек порой считает свои знания об окружающем мире достаточно полными. Однако, за пределами привычной зоны обитания, в действительности, можно обнаружить довольно неожиданные и захватывающие явления. Одно из таких явлений — сверхтекучесть, которая возникает при очень низких температурах, около абсолютного нуля.
Что же такое сверхтекучесть? – Это состояние вещества, находясь в котором оно теряет вязкость (внутреннее трение), в результате чего вещество способно с легкостью проходить через капилляры и узкие щели без какого-либо трения. Так, например, наиболее известное вещество такого рода – сверхтекучий гелий, который может вытекать из сосуда тонкой жидкой пленкой, образовавшейся на стенках этого сосуда. Также благодаря сверхтекучести гелий способен циркулировать по кругу более 18-ти часов без затухания (дальнейшее замедление происходит не по причине трения, а из-за иных квантово-механических явлений).
Ранние эксперименты с жидким гелием
Впервые сверхтекучий гелий получил нидерландский физик и химик Хейке Камерлинг-Оннес в 1908-м году, хотя в то время этот факт не был ясен. Однако, Камерлинг-Оннес сделал несколько важных наблюдений: он измерил плотность гелия, и выяснил, что она достигает своего максимума при 2,17 кельвинов, а измеряя теплоемкость жидкого гелия, он заметил, что ниже этой температуры значения очень сильно отличаются. Впрочем, эти странности ученый списал на экспериментальные погрешности.
Хейке Камерлинг-Оннес (справа) с помощником Герритом Флимом (слева)
В 1922-м году Камерлинг-Оннес зафиксировал еще одно необычное явление. Он поместил открытый дьюаровский сосуд с жидким гелием в другой такой сосуд, также заполненный жидким гелием, в результате чего ожидал, что гелий из внешнего сосуда будет испаряться быстрее, чем гелий из внутреннего. Это вытекает из привычных для нас законов, однако ученый обнаружил одновременное испарение гелия из обеих емкостей. Примечательно было и то, что если перелить гелий из одной емкости в другую, то спустя короткое время уровни жидкости в обоих сосудах выровняются. Данный поразительный эффект был назван эффектом Камерлинга-Оннеса, хотя он был объяснен несколько позже. Как оказалось, гелий образовывал тонкую пленку поверх каждой из емкостей, в результате чего перетекал по этой пленки из одного сосуда в другой.
Пример движение тонкой пленки сверхтекучей жидкости на стенках твердых тел
Гелий II и фазовые переходы второго рода
В 1927-м году датский физик Вильям Кеезом и польский физик Мечислав Вольфке измерили диэлектрическую проницаемость жидкого гелия – физическую характеристику среды, которая определяет отношение напряженности электрического поля к электрической индукции. Ученые подтвердили, что эта характеристика действительно делает заметный прыжок около критической температуры. Проведя также измерение теплопроводности и теплоемкости, они сделали вывод, что в этом состоянии происходит фазовый переход гелия.
Материалы по теме
Ферми-газ
Примечательно, что в отличие от других фазовых переходов (например, из жидкого в газообразное состояние) веществу требуется сколько-нибудь энергии, в то время как такой фазовый переход гелия не требовал энергии вовсе. Также отсутствовала какая-то четкая граница между этими двумя состояниями гелия.
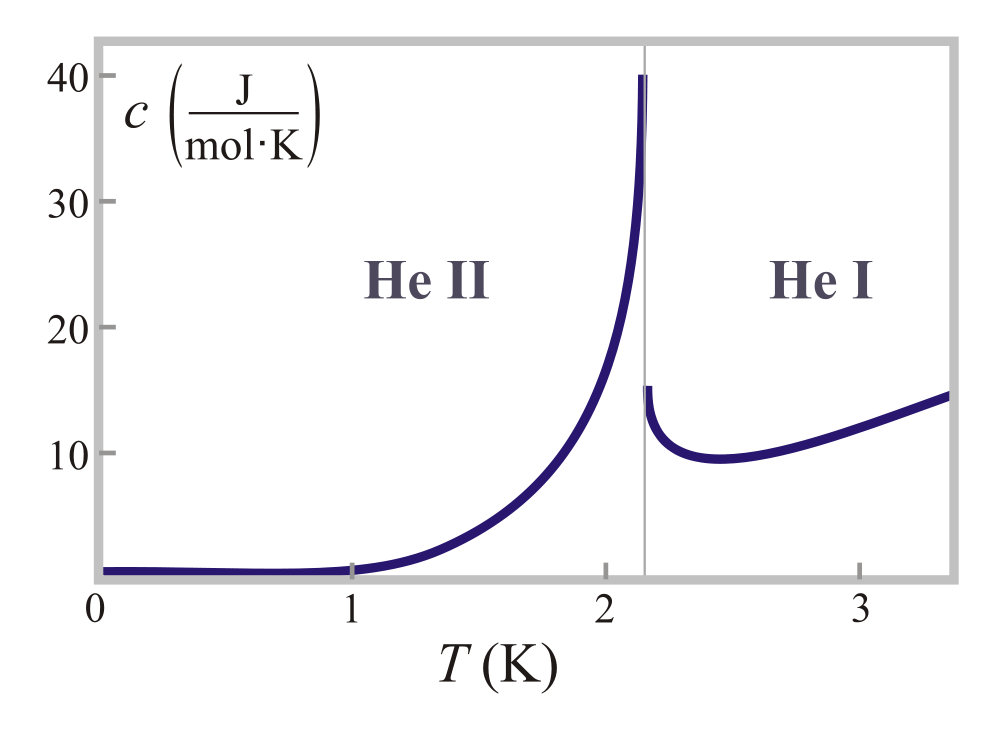
В 1933-м году физик-теоретик Пауль Эренфест создает концепцию фазовых переходов второго рода. Это такие переходы, при которых некоторые характеристики вещества изменяются скачкообразно, в то время как другие – постепенно. Из этого следует, что объем и энергия вещества во время такого фазового перехода – сохраняются, однако меняются характеристики вроде теплоемкости, сжимаемости и тп. Температура, при которой происходит фазовый переход второго рода получила название λ-точка (лямбда-точка) из-за характерной формы графиков нескольких параметров в этой точке. Фазы гелия с температурой выше и ниже критической были названы «гелий I» и «гелий II» соответственно.
Лямбда-переход в жидком гелии: поведение удельной теплоёмкости при низких температурах
Вильям Кеезом считал главной особенностью гелия II – сверхвысокую теплопроводность, что превышала теплопроводность меди при той же температуре в десятки раз.
Открытие сверхтекучести
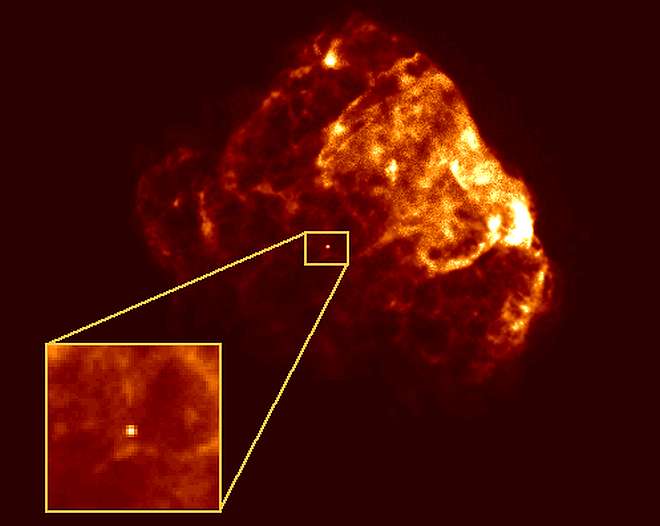
Петр Леонидович Капица, 1930-е годы
В 1938-м году сверхтекучесть была открыта советским физиком Петром Капица, и независимо от него, канадские исследователи Джон Ален и Дон Мисенер показали, что гелий II имеет практически нулевую вязкость. Для этого Капица исследовал протекание через сверхтонкие щели, а Ален и Мисенер – через тонкие капилляры. Именно по причине нулевой вязкости возникали все «странные» вышеупомянутые особенности гелия II. Примечательно, что обе научные работы были опубликованы в одном и том же номере научного журнала Nature. Продолжая исследования в этом направлении, в 1978-м году Капица получил Нобелевскую премию «за фундаментальные открытия в физике низких температур».
Однако непонятным остался тот факт, что вязкость гелия II, измеренная методом колеблющегося диска (в этом методе диск, что колеблется, погружается в жидкость, и исследуются затухания его движения) оказалась ненулевой.
Двухжидкостная модель гелия-II
В 1941-м году советский физик Лев Ландау предложил теорию сверхтекучести, согласно которой гелий II есть смесью двух компонент – обычной и сверхтекучей. При этом сверхтекучая компонента имеет температуру абсолютного нуля, и ее число уменьшается с нагреванием.
Материалы по теме
Конденсат Бозе — Эйнштейна
Переход из основного в возбужденное состояние Ландау связывал с квазичастицами ротонами и фононами, спектр которых должен был иметь особенную форму. Напомним, что квазичастицы представляют собой возбуждения в кристаллах с некоторой волновой функцией. Двухжидкостная модель отлично описывала поведение гелия II и объясняла некоторые особенности вещества.
Ландау не использовал в своей теории явление конденсата Бозе-Эйнштейна (хотя в то время уже возникали способы объяснить сверхтекучесть таким образом), потому что считалось, что активное взаимодействие атомов гелия между собой делает конденсацию невозможной. Однако, в 1947-м году советский математик и физик-теоретик Николай Боголюбов показал, что при некоторых условиях (не слишком высоких скоростях перемещения) этот процесс есть энергетически выгодным, то есть – возможен и даже предпочтителен. Позднее американским физиком Ричардом Фейнманом было показано, что спектр фононов не отвечает тем условиям, которые ставит перед ними теория Ландау. Несмотря на «нефизичность» двухжидкостной модели гелия II Ландау, двухжидкостная гидродинамика отлично работает для решения ряда задач, а потому используется и сегодня. За свои работы, посвященные жидкому гелию, Лев Ландау получил в 1962-м году Нобелевскую премию.
Зависимость состояния гелия от давления (ось ординат) и температуры (ось абсцисс)
Сверхтекучесть гелия-3
В 1947-м году американские исследователи в области криогеники показали, что гелий-3, присутствующий в обычном гелии в небольших концентрациях, не участвует в сверхтекучем движении, что было подтверждением теории о значении конденсата Бозе-Эйнштейна в этом процессе. Дело в том, что обычный гелий является бозе-жидкостью, то есть состоит из бозонов и способен достигать состояния конденсата Бозе-Эйнштейна. В то же время гелий-3 является ферми-жидкостью, то есть состоит из фермионов – неспособных переходить в упомянутое состояние. Напомним, что основным отличием бозонов от фермионов является значение спина – целое и полуцелое – соответственно. В 1949-м году был получен гелий-3 и предсказания об отсутствии у него сверхтекучести подтвердились.
В 1956-м году американский физик Леон Купер предложил механизм сверхпроводимости, согласно которому электроны в проводнике образовывали связанные состояния. Такие пары уже имели целый спин, и конденсация Бозе-Эйнштейна для них работала. По теоретическим предсказаниям, температура гелия-3, способного достичь сверхтекучести, составляла всего несколько микрокельвинов (1/1 000 000 К).
Только в 1972-м году криогеника развилась достаточно, чтоб подтвердить, что при температуре 2,6 мК и давлении в 34 атмосферы – гелий-3 переходит в сверхтекучее состояние. За это открытие в 1996-м году американские физики Дуглас Ошеров, Роберт Ричардсон и Дэвид Ли получили Нобелевскую премию по физике. Также были открыты еще три сверхпроводные фазы гелия-3.
Основные факты о сверхтекучести
Главной особенностью систем, которые находятся в состоянии сверхтекучести – есть перенос массы без потери энергии. Объяснение этого явления скрывается глубоко в квантовой механике.
Грубо говоря – в результате возникновения конденсата Бозе-Эйнштейна некоторые частицы занимают наиболее выгодное энергетическое состояние с нулевым импульсом. В то же время присутствуют частицы с ненулевым импульсом, которые «связаны» с частицами с нулевым импульсом, и потому большая часть частиц вещества находится в т.н. когерентном состоянии. То есть имеет место единое состояние для частиц, которые движутся и которые не движутся, что в итоге приводит к движению вещества без внутреннего трения.
Материалы по теме
Квантовая жидкость и сверхтекучесть
К наиболее «странным» особенностям сверхтекучего состояния можно отнести следующие.
Энтропия в веществе в сверхтекучем состоянии равна нулю и не возрастает.
Теплопроводность при нулевой температуре – бесконечная. То есть в сверхтекучем гелии невозможно установить градиент температур. В таком случае гелий проводит тепло с конечной скоростью, хоть и довольно высокой. Примечательно, что в таком гелии тепло распространяется не по обычным уравнениям теплопроводности, а в виде двойной волны, называемой «вторым звуком».
Тонкие пленки – одно из свойств сверхтекучей жидкости, не раз вводившее в заблуждение исследователей, в первую очередь Камерлинг-Оннеса. Сверхтекучий гелий имеет свойство покрывать тонкой пленкой любую твердую поверхностью, «переползая» по стене вверх, несмотря на силу притяжения. Жидкий гелий невозможно удержать в открытой емкости из-за того, что пленка рано или поздно достигает места с высокой температурой и активно там испаряется. Если две посудины имеют общую стенку, то в результате наличия связывающей их пленки их уровни будут постоянно выравниваться. Пленка сверхтекучей жидкости двигается от места с меньшей температурой к месту с большей температурой. Скорость движения такой пленки растет с уменьшением температуры и может достигать несколько метров в секунду. Пленка сверхтекучей жидкости способна просачиваться через сверхузкие щели. Так для емкости с диаметром горлышка в 5 миллиметров 1 литр жидкого гелия будет вытекать в течение часа.
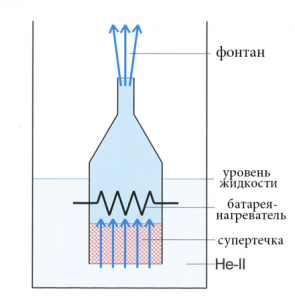
Демонстрация фонтанного эффекта
Фонтанный эффект. Если погрузить колбочку с жидким гелием и нагревателем в ней, в большую емкость гелия, то при работе нагревателя, с колбочки начнет бить фонтан гелия, при том, что количество гелия в колбе не будет уменьшаться. Это явление возникает из-за того, что гелий ІІ легко попадает в колбу, поднимаясь по стенкам, однако нагревшись в ней – вылиться, назад не может. Таким образом, возникает поток гелия в колбу, который компенсируется фонтанированием гелия из нее.
Разная вязкость гелия. Существуют два класса методов измерения вязкости: пропускания через щели и капилляры и измерение действия жидкости на объекты, которые движутся в ней. Для большинства жидкостей эти методы дают похожие численные результаты, в то время как для сверхтекучего гелия ситуация иная. Первый метод дает значения меньшие за погрешность эксперимента (близкое к нулю), а второй – небольшие, но определенные значения. Эта разница может быть объяснена двухжидкостной теорией Ландау: жидкий гелий есть смесь двух компонентов, один из которых имеет нулевую температуру и находится в сверхтекучем состоянии, в то время как другой – нет. Так через щели, в первую очередь, проходит сверхжидкий компонент, тогда как объект, который движется в гелии, наоборот, взаимодействует со вторым компонентом.
Квантовые вихри. Если объект движется в сверхтекучей жидкости (или жидкость быстро течет), то в ней могут образовываться замкнутые контуры потока, которые называют квантовыми вихрями. От обычных вихрей они отличаются тем, что не пропадают со временем.
Сверхтекучесть в иных системах
В 1919-м году тот самый Камерлинг-Оннес открыл квантовое явление протекания электрического тока в твердом теле без потерь, то есть при нулевом электрическом сопротивлении тела, за что получил нобелевскую премию.
В 1995-м году исследователям удалось провести эксперимент, в результате которого разреженный газ при низких температурах перешел в состояние конденсата Бозе-Эйнштейна. Этот газ вел себя точно также как и сверхтекучая жидкость. Дальнейшие эксперименты показали, что тела, движущиеся(с ограниченным диапазоном скоростей) сквозь конденсат не испытывали какое-либо изменение в значении энергии, то есть обмен энергии отсутствовал.
Материалы по теме
Сверхкритическая жидкость
В 2000-м году американский ученый Ян Петер Тоэнниэс добился сверхтекучего состояния для водорода (при температуре 0,15 К). В 2005-м году была обнаружена сверхтекучесть в разреженном фермионом газе при низких температурах.
В 2004-м году исследователи из Пенсильванского университета смогли перевести твердый гелий в сверхтекучее состояние, однако результаты этой работы не были признаны научным сообществом. В 2009-м году исследователи из Калифорнийского университета в Беркли получили сверхтекучее состояние для твердого рубидия. Упорядоченная структура рубидия была схожа со структурой кристалла, и занимала несколько микрометров. Все атомы рубидия находились в одном квантовом состоянии. Такое состояние было названо «supersolid» (сверхтвердый).
Высокотемпературная сверхтекучесть
Помимо сверхтекучего электрического тока, твердого тела или газа, в 2017-м году была также открыта и экспериментально подтверждена более экзотическая система — фотонное сверхтекучее вещество. Исследователи с CNR NANOTEC в Лечче, Италия, и канадского Политехнического университета Монреаля смогли создать фотонное сверхтекучее вещество при комнатной температуре.
Профессор канадского Политехнического университета Монреаля, Стефан Кена-Кохкен
Простыми словами – ученые поместили между двух мощных зеркал тонкий слой (100 нанометров) органических молекул и «запустили» фотоны. Частицы света поочередно отбивались от каждого зеркала, протекая через вещество между зеркалами. С помощью сконструированного устройства исследователям удалось получить поляритоны – квазичастицы, возникающие в результате взаимодействия фотонов с возбужденной окружающей средой. Возбуждая эти поляритоны при помощи лазера, удалось заставить фотоны «огибать» препятствующие им ранее частицы.
Применение явления сверхтекучести
Как и с любыми фундаментальными открытиями, сверхтекучесть не имеет какого-либо определенного и популярного применения. На сегодня – это лишь интересное и плохо изученное явление, которое находит применение в очень специфических областях. Так, сверхтекучий гелий используется для охлаждения нагревающихся систем. В перспективе, такой охладитель будет применен для охлаждения сложнейших конструкций, в силу своих способностей – проникать в мельчайшие щели и самостоятельно двигаться в сторону источника тепла.
Дальнейшее изучение сверхтекучести даст более подробное описание этого явления, позволит лучше понять его природу, и тогда появится возможность управлять им и использовать его в бытовых целях.
Похожие статьи
Понравилась запись? Расскажи о ней друзьям!