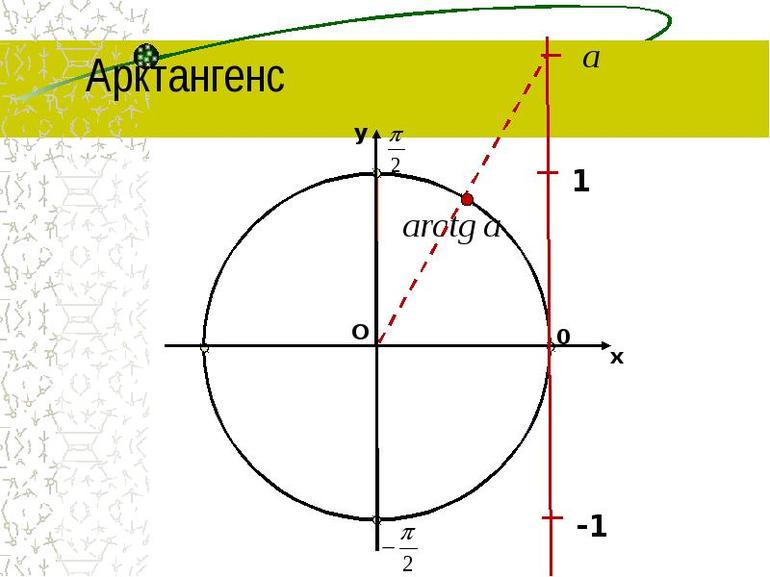
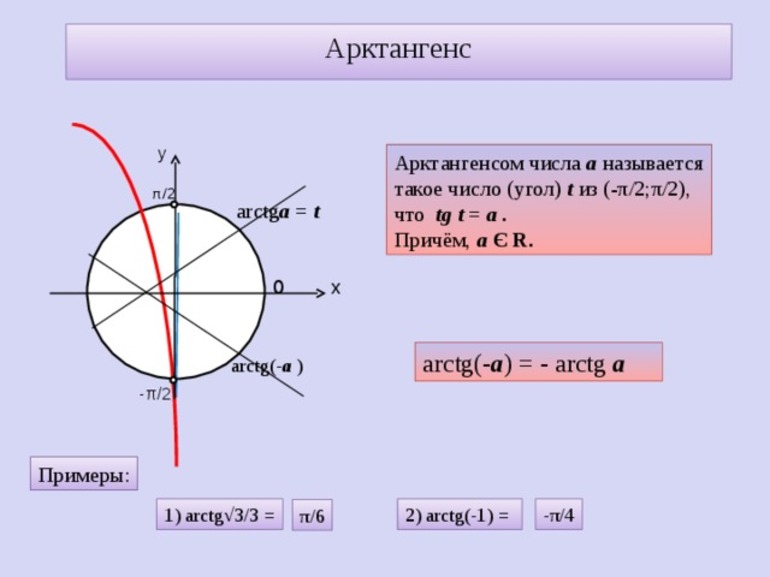
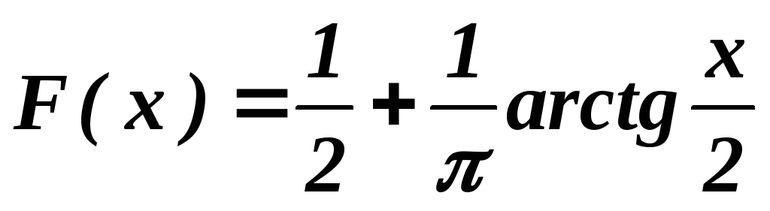какие значения может принимать арктангенс
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Для четкого понимания рассмотрим пример.
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Основные значения arcsin, arccos, arctg и arctg
Таблица синусов основных углов предлагает такие результаты значений углов:
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
Следуя из таблицы, находим значения арккосинуса:
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
| α | — 3 | — 1 | — 3 3 | 0 | 3 3 | 1 | 3 | |
| a r c t g a к а к у г о л | в р а д и а н а х | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
| в г р а д у с а х | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° | |
| a r c t g a к а к ч и с л о | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 | |
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Нахождение значения arcsin, arccos, arctg и arcctg
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
Арктангенс- определение, свойства и формулы
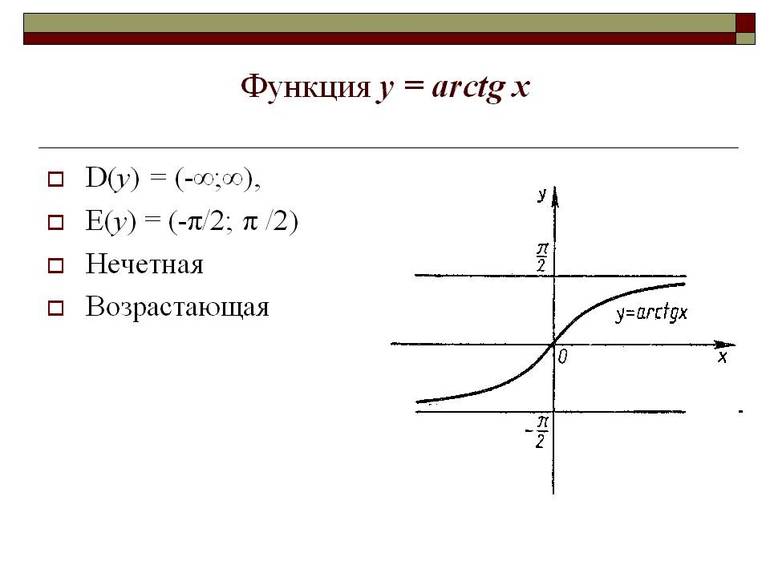
Чётность и возрастание
Чтобы получить график арктангенса, используется кривая тангенса путём замены местами осей ординат и абсцисс. Для устранения многозначности используется интервал, на котором функция монотонна. Это определение считается основным значением арктангенса. Если показатель отрицательный, значит функция нечётная.
Главное свойство arctg — бесконечность на его области определения (для числа х). Так как y = arctg x, где y равен нулю, тогда x = 0, значит и arctg 0. При выполнении расчётов используется таблица арктангенсов.
В ней указаны значения в градусах и радианах, при определённых данных аргумента. Если вычисления выполняются на математическом веб-ресурсе, пользователю предоставляется возможность бесплатно использовать онлайн-калькулятор и таблицу Брадиса. Можно вычислить синус, косинус, производную арктангенса в экселе либо с помощью языка программирования Паскаль.
Чтобы посчитать величину правильно, используются свойства функций. При помощи определения арксинуса выполняется уравнение sin (arcsin a)=a. Свойства других величин:
В первых двух свойствах соблюдается условие −1≤a≤1. Если значение а выходит за указанные пределы, тогда функции нет смысла определять. Учитывая свойства синуса арксинуса, нельзя записать sin (arcsin8)=8, так как выражение sin (arcsin8) не имеет смысла. Аналогичный ответ получается, если необходимо определить разность арккосинуса sqrt (квадратный корень) из пяти.
Противоположные числа
Формулы, с помощью которых производится расчёт связи между производными: arcsin (-a)=-arcsina, arccos (-a)=пи-arccosa, arctg (-a)=-arctga, arcctg (-a)=пи-arcctga. Должно соблюдаться условие −1≤a≤1. Если а принадлежит промежутку −∞ до +∞, тогда arctg (−a), и arcctg (−a).
Чтобы доказать первое отношение с противоположными числами, рассматривается определение arcsin (−a). Число либо угол находится в пределах −π/2-π/2 и синус, равный −a. Учитывая определение арксинуса, можно записать следующее равенство: −π/2≤arcsin a≤π/2.
Необходимо доказать, что sin (−arcsin a)=−a. Для этого рекомендуется придерживаться свойств противоположных углов. Из рассмотренных примеров можно сделать вывод: sin (−arcsin a)=−sin (arcsin a)=−a.
Аналогичным способом можно доказать, что arccos (−a)=π−arccos a. Используя определение производной функции, подтверждается, что π−arccos a — угол либо число, значение которого колеблется в пределах 0-π, а cos (π−arccos a)=−a. Придерживаясь определения арккосинуса числа, выполняется неравенство 0≤arccos a≤π.
Если средняя часть уравнения равняется −a, тогда, придерживаясь формулы приведения, записывается следующее равенство cos (π−arccos a)=−cos (arcos a). С помощью свойства производной косинуса завершается доказательство cos (π−arccos a)=−cos (arcos a)=−a. Аналогичной схемы рекомендуется придерживаться при рассмотрении свойств арккотангенсов и арктангенсов противоположных знаков. Плюс утверждения — возможность избавиться от вычисления производных функций отрицательных чисел.
Сложение величин
Свойство, согласно которому устанавливается связь между arccos arcsin числа а, и между arctg и arcctg переменной, записывается следующим образом: arcsina+arccosa=пи/2, arctga+arcctga=пи/2. Чтобы доказать первую часть равенства, где расписана сумма производных синуса и косинуса числа а, делённая на два, необходимо рассмотреть следующую запись: arcsin a=π/2−arccos a.
Основываясь на определение арксинуса, можно доказать, что выражение верно, когда π/2−arccos a — угол (цифровое значение), лежащий на промежутке −π/2 до π/2, а синус угла равен а. Чтобы показать такую действительность, используется определение арккосинуса и равенство 0≤arccos a≤π. Последнее выражение считается справедливым.
С учётом свойств неравенств, умножаются части на минус один, изменяются знаки. Полученные значения суммируются с числом π/2. Выполнив перечисленные действия, получается неравенство −π/2≤π/2−arccosa≤π/2. Чтобы показать, что sin (π/2−arccos a)=a, используется формула приведения, свойство производной функции косинус.
Доказано, что сумма arccos и arccos a равна π/2. Аналогично понадобится доказать, что сумма арккотангенса числа a и арктангенса равняется π/2. Главное предназначение таких свойств заключается в том, что они выражают арксинус через акрккосинус одного числа, а также арккотангенс через арктангенс и наоборот.
Примеры и задачи
Задания на свойства функций и их производных от числа либо угла можно решить с помощью разных программ: excel, pascal. Действия будут зависеть от условий задачи. Решение должно основываться на основные признаки, доказанные либо утверждённые равенства. Свойствам производных отвечают следующие выражения:
Равенства при определённых условий следуют из определений функций числа. Чтобы понять утверждения, необходимо доказать: arcsin (sin α)=α, при этом должно выполняться требование −π/2≤α≤π/2. Аналогичным образом доказываются оставшиеся свойства. Если обозначить sin α=а, которое находится на отрезке [−1, 1], тогда получится выражение arcsin (sin α)=α, то есть arcsin a=α. Известно из условий задач, что −π/2≤α≤π/2. При решении через а обозначили sin α.
Поэтому можно записать, что arcsin a=α, что эквивалентно определению производной функции синуса. Вывод: arcsin (sin α)=α при условии, что −π/2≤α≤π/2. Разные свойства, связанные с синусом и косинусом, тангенсом и котангенсом, можно применить на практике.
Запись arccos (cos α) правдивая, не только при условии, что 0≤α≤π. Выражение arccos (cos α)=α считается справедливым только при таком условии. Поэтому arccos (cos (−3π))=−3π не верно, так как −3π не принадлежит указанному отрезку. Схожие утверждения логичны и для arcctg (ctg α), arctg (tg α).
Используя определение всех функций, их признаки, тригонометрические формула можно получить другие равенства и уравнения, в которых отображается связь между arcsin, arcctg, arctg и arccos. Чтобы быстро решать задачи на данную тематику, рекомендуется выучить некоторые утверждённые равенства (arcsin 0=0, arccos 1=0, как угол arccos (-1)=180 градусов). Они описаны в специальных таблицах, которые можно найти в глобальной сети либо в учебниках по математике.
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса.
Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса данного числа. Сначала мы внесем ясность, что называется значением арксинуса, арккосинуса, арктангенса и арккотангенса. Дальше получим основные значения этих аркфункций, после чего разберемся, как находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса. Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.
Навигация по странице.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса».
Для этого обратимся к определениям арксинуса, арккосинуса, арктангенса и арккотангенса числа. Если под арксинусом, арккосинусом, арктангенсом и арккотангенсом числа a понимать угол, то значением арксинуса, арккосинуса, арктангенса и арккотангенса числа a логично считать величину этого угла. Если под арксинусом, арккосинусом, арктангенсом и арккотангенсом числа a понимать число, то оно и является значением соответствующей аркфункции.
Чтобы окончательно все стало понятно, приведем пример.
Основные значения arcsin, arccos, arctg и arcctg
Из таблицы синусов основных углов мы можем извлечь следующие результаты:
Для удобства запишем основные значения арксинуса в таблицу. Основные значения арксинуса (как и приведенные ниже значения арккосинуса, арктангенса и арккотангенса) желательно выучить наизусть, так как с ними придется часто встречаться при решении примеров и задач.
Чтобы получить основные значения арккосинуса, обратимся к таблице косинусов основных углов. Из нее находим, что
Отсюда получаем такие значения арккосинуса:
Вот соответствующая таблица арккосинусов.
Аналогично находятся основные значения арктангенса и арккотангенса. Также занесем их в таблицы арктангенсов и арккотангенсов.

Нахождение значений arcsin, arccos, arctg и arcctg по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса. Будем это делать на примерах.
Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).
Нахождение значения arcsin через arccos, arctg, arcctg и т.п.
Задача нахождения значения арксинуса числа через известный арккосинус этого числа, арккосинуса через известный арксинус, арктангенса через арккотангенс и арккотангенса через известный арктангенс решается очень просто – достаточно использовать формулы arcsin a+arccos a=π/2 и arctg a+arcctg a=π/2 (смотрите формулы суммы арксинуса и арккосинуса, суммы арктангенса и арккотангенса).
Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a требуется найти значение арктангенса или арккотангенса этого числа a или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg.
Арксинус, арккосинус, арктангенс и арккотангенс числа: основные свойства
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса
Это свойство используется чаще всего, поэтому логичнее всего начать рассмотрение всех основных свойств именно с него. Рассмотрим, чему равны синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа.
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа
Данное свойство следует напрямую из определения арксинуса, арккосинуса, арктангенса и арккотангенса.
sin ( a r c sin a ) = a
Доказательство для арккосинуса, арктангенса и арккотангенса строится аналогично, на базе определений этих функций. Вот несколько примеров использования данного свойства.
Пример 1. Свойства обратных тригонометрических функций
Арксинус, арккосинус, арктангенс и арккотангенс противоположных чисел
Существует связь между арксинусами, арккосинусами, арктангенсами и арккотангенсами противоположных чисел. Запишем соотношения, выражающие ее.
arcsin, arccos, arctg и arcctg противоположных чисел
Доказательство свойства арксинусов противоположных чисел завершено.
Теперь рассмотрим доказательство свойства арккосинусов противоположных чисел.
Доказательства для арктангенса и арккотангенса проводится по аналогичному принципу.
Сумма арксинуса и арккосинуса, арктангенса и арккотангенса
Данное свойство устанавливает связь соответственно между арксинусом и арккосинусам, арктангенсом и арккотангенсом. Запишем формулы для арксинуса и арккосинуса.
Сумма arcsin и arccos
Соответственно, для арктангенса и арккотангенса
Сумма arctg и arcctg
Пользуясь разобранными свойствами, можно выряжать арксинус через арккосинус, арккосинус через арксинус, арктангенс через арккотангенс и наоборот.
Пример 2. Сумма арксинуса и арккосинуса
Арксинус синуса, арккосинус косинуса, арктангенс тангенса и арккотангенс котангенса
Запишем соотношения, иллюстрирующие свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
Свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса
Аналогично, соблюдение условий обязательно для арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
К примеру, запись a r c sin ( sin 8 π 3 ) = 8 π 3 будет ошибочной, так как число 8 π 3 не удовлетворяет условиям неравенства.
Описанные в этой статье свойства позволяют получить ряд полезных формул, определяющих связи между основными и обратными тригонометрическими функциями. Соотношениям, связывающим sin, cos, tg, ctg, arcsin, arccos, arctg и arcctg будет посвящена отдельная статья.
Арктангенс и арккотангенс. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти арксинус и арккосинус от числа. Результат можно видеть как в градусах, так и в радианах. Теоретическую часть и численные примеры смотрите ниже.
Арктангенс и арккотангенс − теория, примеры и решения
Функция арктангенс и ее график
 |
Однако, функцию тангенс можно разделить на интервалы, где она монотонна. Эти интервалы:
 , ,  , ,  , ,  и т.д. и т.д. |
По теореме об обратной функции, на каждом из указанных отрезков функция tg x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке 
Функция (1) − это функция, обратная к функции
График функции арктангенс можно получить из графика функции 
 |
Свойства функции арктангенс.
Решим тригонометрическое уравнение
В интервале 
Следовательно в интервале 
Решение уравнения (2) представлен на Рис.3:
 |
Так как tg t − это ординат точки пересечения прямой OMt1 c прямым x=1, то для любого a на линии тангенса есть только одна точка T(1; a). Прямая OTt пересекается с окружностью с радиусом 1 в двух точках: 



Пример 1. Решить тригонометрическое уравнение:
Решение. Воспользуемся формулой (3):
Пример 2. Решить тригонометрическое уравнение:
Решение. Воспользуемся формулой (3):
Используя онлайн калькулятор получим:
Функция арккотангенс и ее график
 |
Однако, функцию кокотангенс можно разделить на интервалы, где она монотонна. Эти интервалы:
  |
По теореме об обратной функции, на каждом из указанных интервалов функция ctg x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке 
Функция (4) − это функция, обратная к функции
График функции арккотангенс можно получить из графика функции 
 |
Свойства функции арккотангенс.
Решим тригонометрическое уравнение
В интервале (0; π) для уравнения (5) существует одно t, для которого сtg t=a. Это t=arcctg a. Следовательно в интервале (0; π) уравнение (5) имеет один корень. Так как котангенс периодичная функция с основным периодом π, то общее решение уравнения (5) имеет следующий вид:
Решения уравнения (5) можно представить на единичной окружности (Рис.6):
 |
ctg t − это абсцис точки пересечения прямой 





Пример 1. Решить тригонометрическое уравнение:
Решение. Воcпользуемся формулой (6):
Так как в интервале (0; π)
Пример 2. Решить следующее тригонометрическое уравнение:
Решение. Используя формулу (6), имеем
С помощью онлайн калькулятора вычисляем