какие значения принимает 1 бит
Какие значения принимает 1 бит
Бит (англ. binary digit ; также игра слов: англ. bit — немного) (один двоичный разряд в двоичной системе счисления) — одна из самых известных единиц измерения количества информации. Обозначается по ГОСТ 8.417-2002. Для образования кратных единиц применяется с приставками СИ и с двоичными приставками.
Клод Шэннон в 1948 г предложил использовать слово bit для обозначения наименьшей единицы информации в статье A Mathematical Theory of Communication.
В зависимости от точек зрения, бит может определяться следующими способами:
Возможны две физические (в частности электронные) реализации бита (одного двоичного разряда):
В вычислительной технике и сетях передачи данных обычно значения 0 и 1 передаются различными уровнями напряжения либо тока. Например, в микросхемах на основе ТТЛ 0 представляется напряжением в диапазоне от +0 до +0,8 В, а 1 в диапазоне от +2,4 до +5,0 В.
В вычислительной технике, особенно в документации и стандартах, слово «бит» часто применяется в значении «двоичный разряд». Например: старший бит — старший двоичный разряд байта или слова, о котором идёт речь.
Аналогом бита в квантовых компьютерах является кубит (q-бит).
Двоичные логарифмы других оснований
Замена логарифма 2 на e, 3 или 10 приводит соответственно к редко употребляемым единицам нат, трит и хартли=дит, равным соответственно 
Какие значения принимает 1 бит
Биты теперь часто собираются в группы по 8, кластер, известный как байт. [2] Половина байта или 4 бита данных называется съедобным. [3] Хотя обглёвывание не часто используется в качестве общей единицы измерения данных, биты и байты иногда ошибочно заменяются. Байт содержит 8 бит и отображается в виде единицы измерения при вводе заглавной буквы «B». Бит является наименьшей единицей данных и представлен маленькой буквой «b»,
История
Концептуализация единицы измерения информации была представлена Клодом Шенноном в 1948 году. [4] Работая в Bell Labs в 1940-х годах, он опубликовал двухчастную статью в июле и октябре 1948 года в Техническом журнале Bell Systems Technical Journal, озаглавленную «Математическая теория коммуникации». [5] Эти концепции легли в основу Теории информации, которая сосредоточена на количественной оценке, хранении и применении в области передачи информации или данных. [6] Это революционизировало концепцию данных в технологии, как это было тогда, ранее, рассматривалось как потоки, импульсы и волны, передаваемые через аналоговые сигналы, которые прерывались шумами и помехами связи, приводящими к неточной и ошибочной передаче данных.
По словам Шеннон, «информация в сигнале совершенно отделена от смысла сообщения». Заимствуя термин «бит» у Джона Тьюки, его коллеги по работе в Bell Labs, который сократил термин двоичная цифра, Шеннон описала использование битов для представления 2 возможных состояний, заложив тем самым основы теории информации. Шеннон называют «Отцом теории информации», а иногда и «Отцом кусочка».
Функциональность
В современных устройствах биты часто считываются разными состояниями электрического напряжения, импульса тока или электрического состояния флип-флоп цепи. Термин «бит в секунду» (бит в секунду) используется для измерения скорости передачи данных из Интернета. [7] Хотя это также может обозначаться в «байтах в секунду» (Bps), большинство провайдеров Интернет-услуг используют байты в секунду. «Биты» также широко используется для представления возможностей процессора. Однако, с точки зрения хранения данных, вместо них часто используются «байты».
Подразделения
Бит может быть использован либо для отображения того, сколько информации присутствует, либо для отображения того, сколько устройство способно хранить. Биты в секунду (бит/с) показывают скорость передачи данных. Однако бит часто используется не в одиночку, а префиксом с метрическими префиксами, такими как Kilo-, Mega-, Giga- и Tera-, которые используются для отображения все большего количества информации. [8]
| Префиксное устройство | Эквивалент в битах |
|---|---|
| Килобит (Кб) | (1000^1)1,000 бит. |
| Мегабит (Мб) | (1000^2)1,000,000 битов |
| Гигабит (Гб) | (1000^3)1,000,000,000,000 битов |
| Терабит (Tb) | (1000^4)1,000,000,000,000,000 битов |
Те же самые префиксы используются для отображения более высоких скоростей передачи данных и приводят к таким показателям скорости, как Kbps, Mbps, Gbps и так далее. Современные технологии теперь могут обеспечивать скорость передачи данных почти 100 Гбит/с в высокоразвитых регионах, но большинство домохозяйств все еще сохраняют более низкую скорость Интернета, при этом средняя скорость передачи данных в Интернете составляет менее 10 Мбит/с. [10]
Бит | Байт | Системы счисления
Для полноты понимания работы микроконтроллера необходимо четко знать, что такое бит и байт, а также уметь применять различные системы счисления.
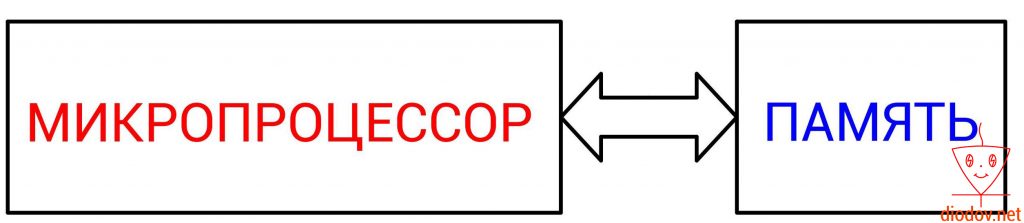
Основным вычислительным ядром любого микроконтроллера является микропроцессор. Именно он выполняет обработку команд или же кода, написанного программистом.
Упрощенно работу микропроцессора можно представить следующим образом. Сначала выполняется считывание данных из определенной ячейки памяти, далее выполняется их обработка и затем возвращение результата назад в ячейку памяти. Следовательно, для того, чтобы микропроцессор мог выполнять свои функции необходимо наличие памяти. Иначе ему неоткуда будет считывать данные, а затем некуда помещать результаты вычислений.
Давайте кратко рассмотрим алгоритм работы микропроцессора (МП) на примере сложения двух цифр.
Вот такой монотонной работой занимаются микропроцессоры. Для выполнения одной команды ему необходимо выполнить четыре операции. Однако современные МП выполняют более 1 000 000 000 операций за одну секунду. Микроконтроллеры же выполняют более 1 000 000 операций, чего, как правило, предостаточно для такого крохотного устройства.
Данные, с которыми оперирует микропроцессор, представляют собой набор цифр. Поэтому нашей целью является рассмотреть, какие цифры, а точнее системы счисления “понимает” микроконтроллер.
Десятичная система счисления
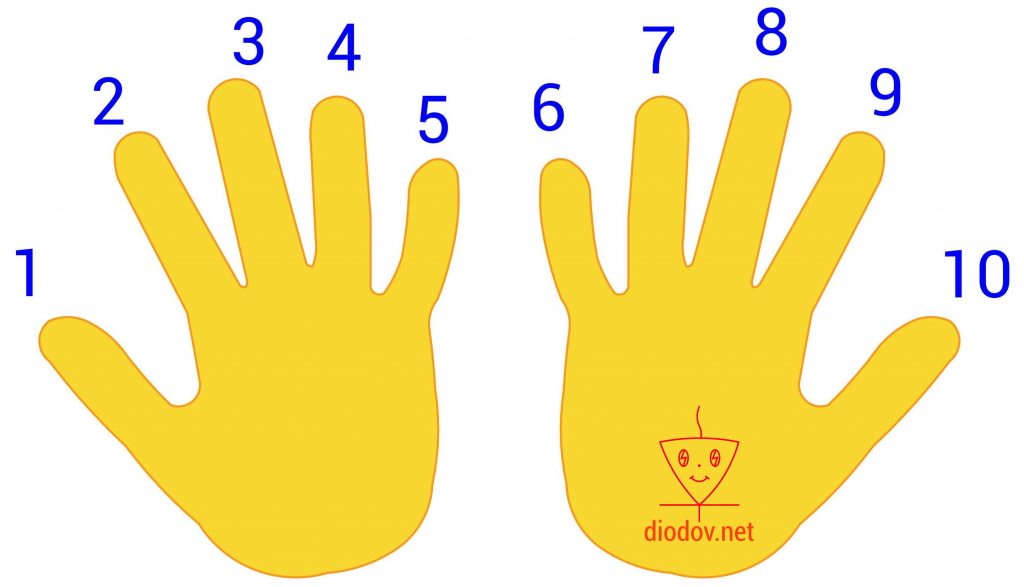
Десятичная система счисления нам очень близка и понятна. Возникла она очень давно, когда у людей впервые возникал необходимость подсчета чего-либо, например количества дней или определённых событий. Поскольку в те давние времена не было каких-либо технических устройств, то люди использовали для счета пальцы рук. Загибая или разгибая пальцы можно получить десять комбинаций, что очень просто и наглядно.
Математически данная она состоит из десяти разных символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, поэтому она и называется десятичной. С помощью указанных символов легко отобразить любое число.
Основанием десятичной системы является 10. Когда при счете использованы все знаки от 0 до 9, то, чтобы продолжить дальнейший счет, необходимо вместо символа 9 поставить символ 0, т. е. обнулить предыдущее значение, а слева от нуля записать символ 1. И так можно продолжать счет до бесконечности, прибавляя слева от текущей позиции цифры последующую.
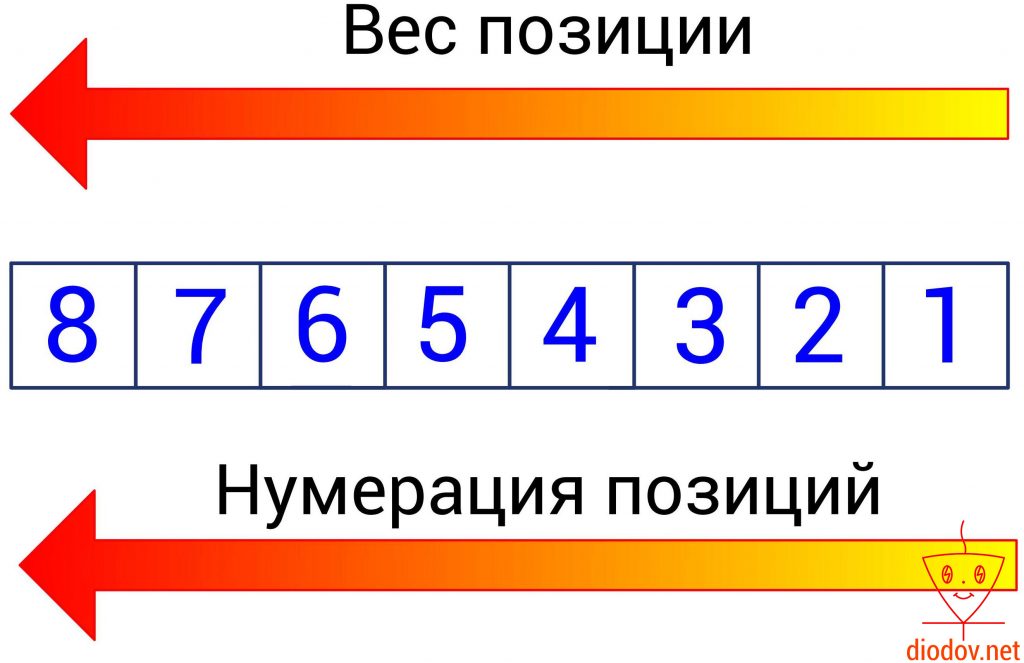
Каждая позиция цифры имеет свой вес. Наименьший вес имеет позиции, находящаяся в крайнем правом положении. По мере перемещения слева на право, вес позиции возрастает.
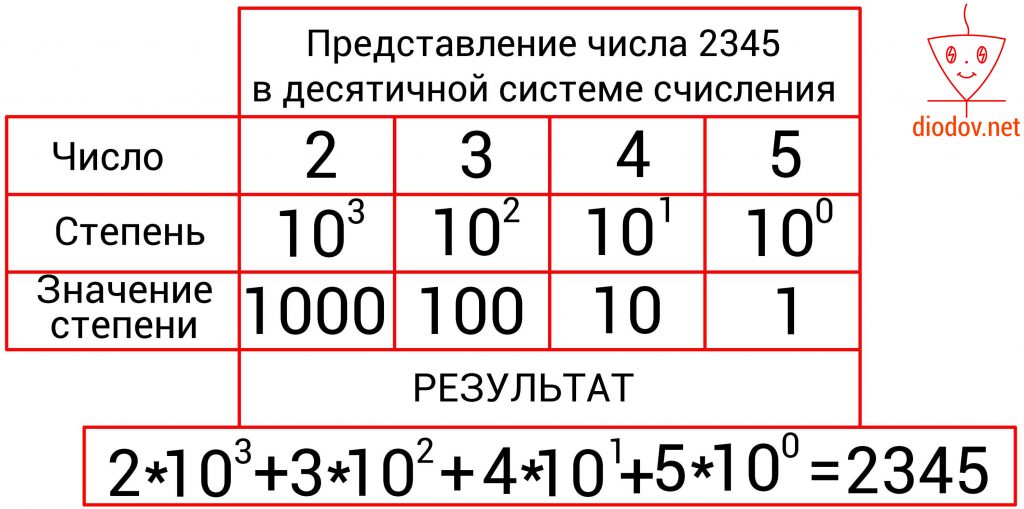
Например, число 2345 имеет 4 позиции. В крайней левой позиции отображаются единицы, в данном случае 5 единиц, а степень 10 имеет нулевое значение. Далее вес позиции увеличивается. Следующее значение, расположенное слева от предыдущего, уже содержит десятки, а 10 имеет степень 1, поэтому во второй позиции числа 2345 четыре десятка.
Двоичная система счисления
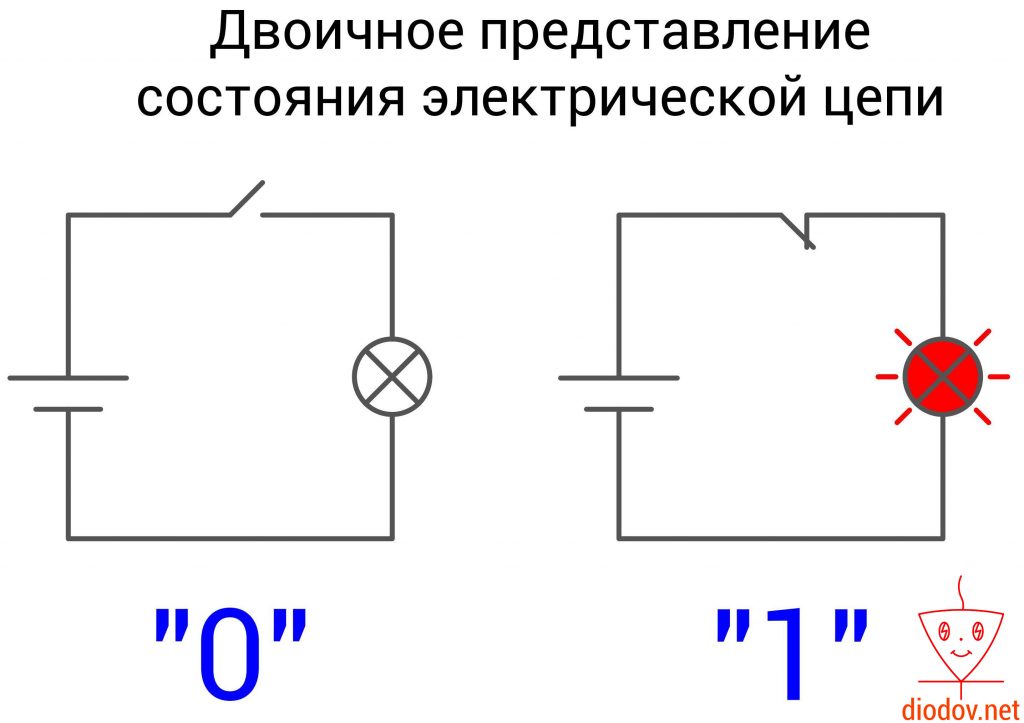
Двоичная система счисления оперирует всего лишь двумя символами 0 и 1. Она повсеместно применяется в цифровой технике, поскольку очень удачно сочетается с двумя устойчивыми состояниями электрической цепей: включено и выключено либо есть сигнал и нет сигнала. Также нулем еще обозначают сигнал низкого уровня, а единицей – высокого.
Порядок записи двоичного числа полностью соответствует десятичному. Веса позиций также возрастают справа налево. Только основанием является 2, а не 10.
Чтобы отличать двоичную систему от десятичной в цифровой технике используют индекс 2 и 10 соответственно:
110110 – десятичное.
При написании кода программы для обозначения двоичного значения перед ним ставится префикс 0b, например 0b11010101. Если записывается десятичное, то перед ним ничего не ставится.
0b11010101 – двоичное;
11010101 – десятичное.
Бит и байт
Двоичная система счисления также используется при хранении и обработке информации.
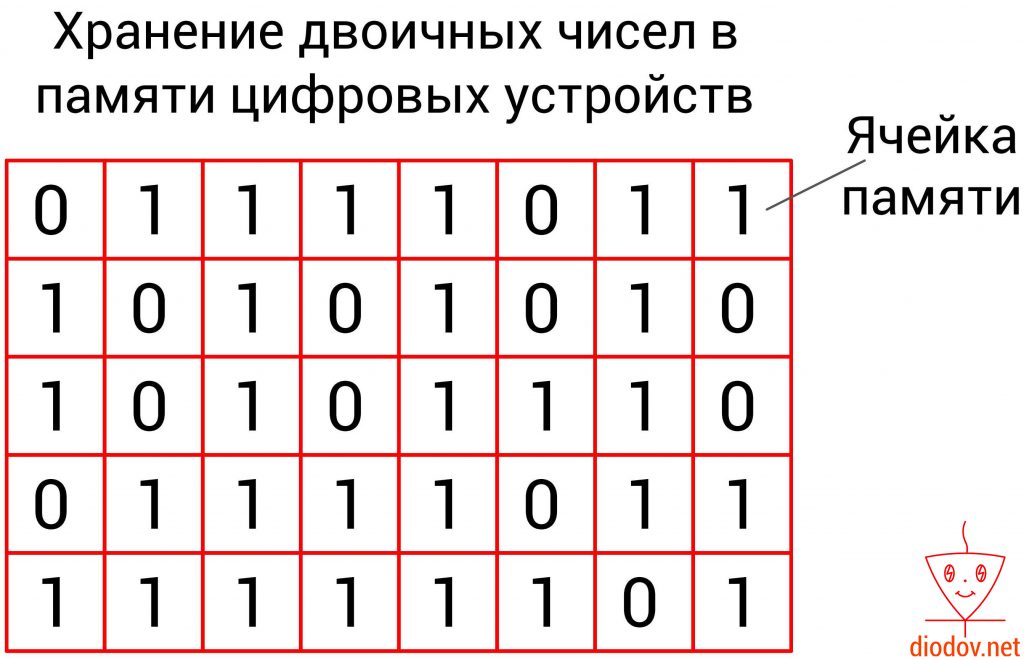
Вся информация цифровых запоминающих устройств хранится в памяти. Память представляет собой набор ячеек.
Каждая ячейка содержит один бит данных. Бит – это единица измерения объема памяти. В одном бите можно запоминать максимум два значения: 0 – это одно значение, а 1 – второе.
Bit происходит от двух английских слов Binary Digit (двоичное число).
При работе с битами регистров микроконтроллера мы будем часто обращаться к таким понятиям, как старший и младший биты. Эти понятия строго регламентированы. В двоичной системе разряд, который имеет самую правую позицию, получил название младший значащий бит (МЗБ). В англоязычной литературе его называют Least Significant Bit (LSB). Именно с него начинается нумерация битов.
Наибольший вес имеет бит, находящийся в самой левой ячейке памяти. Его принято называть старший значащий бит (СЗБ) или Most Significant Bit – MSB.
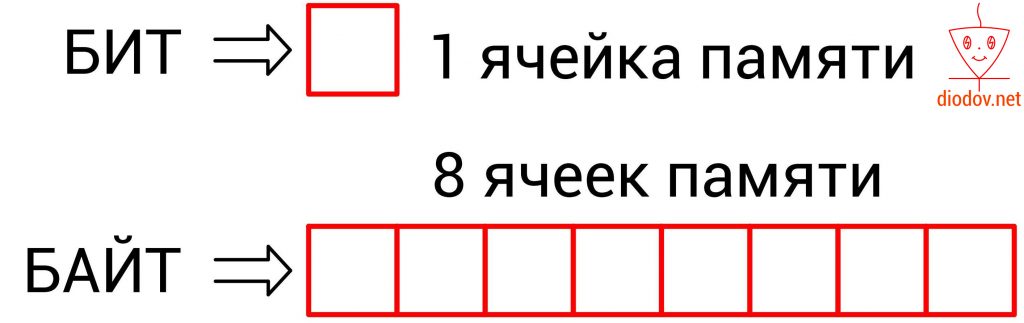
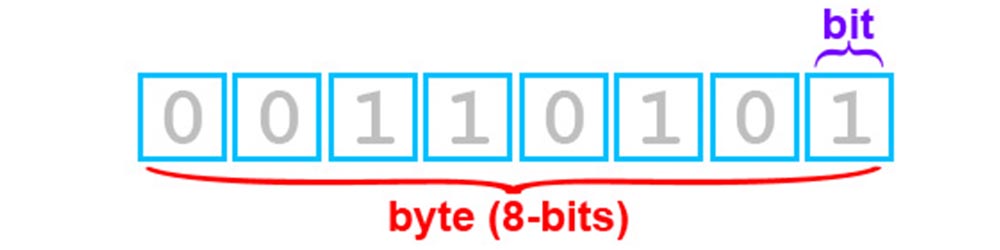
Более емкой единицей информации является байт (byte). Он равен 8 битам, т. е. восемь элементарных ячеек памяти составляют один байт.
1 байт = 8 бит
В одном бите можно хранить только два разных значения или две комбинации. А в 1 байте можно хранить 256 различных комбинаций. Ровно столько же символов содержится в таблице кодировки ASCII. Но об этом в другой раз.
На практике пользуются большими значениями объёма памяти килобайтами, мегабайтами, гигабайтами и терабайтами.
1 килобайт (кБ) = 1024 байт
1 мегабайт (МБ) = 1024 кБ
1 гигабайт (ГБ) = 1024 МБ
1 терабайт (ТБ) = 1024 ГБ
Преобразование десятичного числа в двоичное
На практике программисты часто пользуются несколькими системами счисления. Поэтому следует научиться переводить числа из десятичной системы в двоичную. Здесь можно выделить два простых способа. Рассмотрим их по порядку.
Первый способ заключается в том, что десятичное число непрерывно делится на два. При этом учитывается полностью ли оно разделилось или с остатком. Если значение делится без остатка, как например 4/2 = ровно 2 или 6/2 = ровно 3, то записывается ноль, а если с остатком, как 3/2 или 5/2, то записывается единица.
Теперь давайте переведем число 125 в двоичную форму.
125/2 = 62 остаток 1
Получаем двоичное число 11111012
Я надеюсь здесь понятно, что если 1 разделить на 2, то математически ноль никак не получится, однако такой подход позволяет объяснить данный алгоритм.
Второй способ
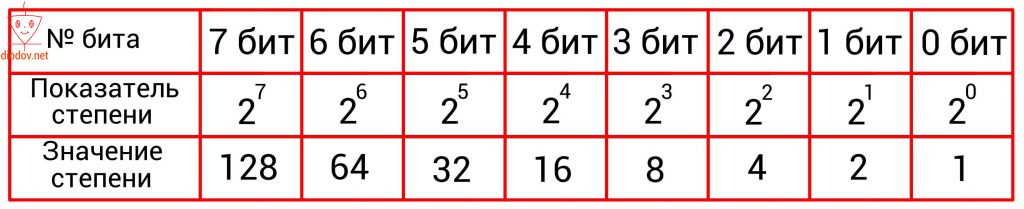
Второй способ имеет такую идею. С изначального числа нужно вычесть число в степени два, которое будет меньше заданного значения. Для ускорения процесса преобразования воспользуемся следующей таблицей.
Давайте преобразуем 125.
Следует обратить особое внимание на то, что нумерация битов, во-первых, выполняется справа налево, а во-вторых начинается с нуля! Это несколько непривычно, поскольку в десятичной системе счисления счет принято начинать с единицы. Однако в цифровой технике счет всегда идет с нуля! К этому следует приучить себя заранее, так как при написании программ для микроконтроллеров мы все время будем начинать счет битов с нуля. В дальнейшем вы такому счету быстро привыкнете, поскольку и в техническом описании МК строго соблюдается данное правило.
Преобразование двоичного числа в десятичное
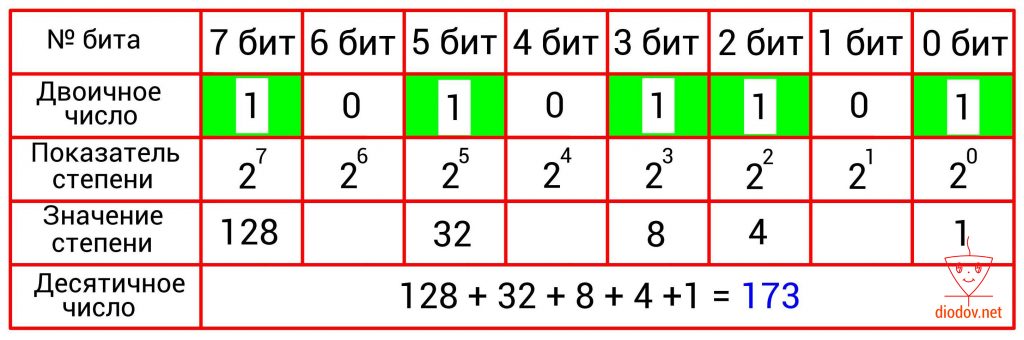
Преобразование двоичного числа в десятичное выполняется довольно просто. Для этого следует сложить десятичные веса всех двоичных разрядов, в которых имеются единицы. Биты, в которых записан ноль, пропускаются. В качестве примера возьмем такое значение: 10101101. Нулевой, второй, третий, пятый и седьмой биты имеют единицы. Получаем: 2 0 + 2 2 + 2 3 + 2 5 + 2 7 = 1 + 4 +8 + 32 + 128 = 173.
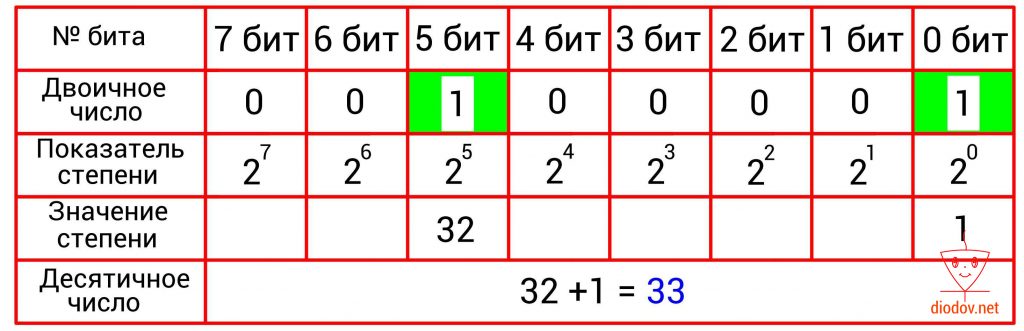
В таблицах, приведенных ниже, наглядно показано перевод чисел из двоичной в десятичную систему счисления.
Шестнадцатеричная система счисления
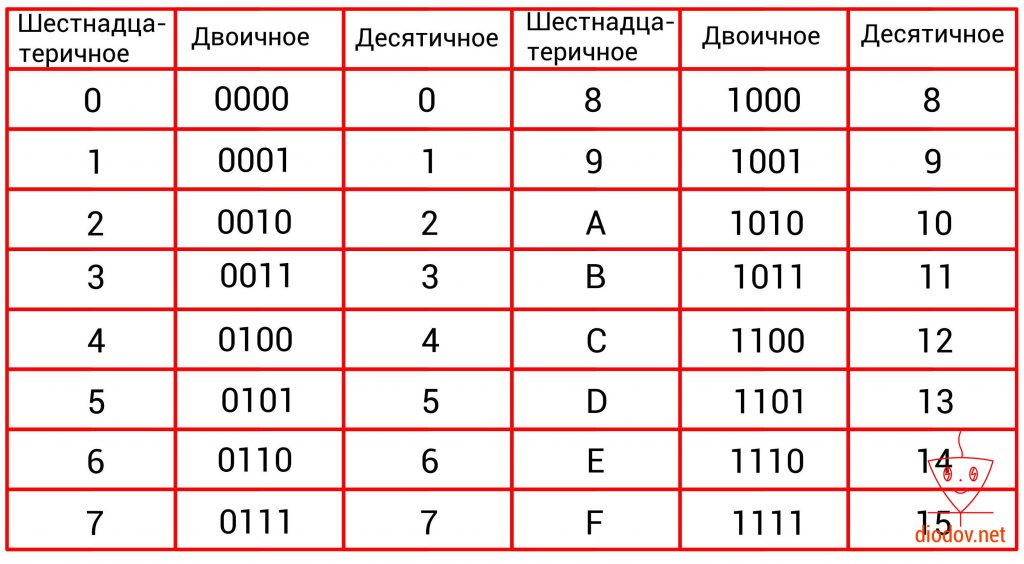
В программировании микроконтроллеров очень часто пользуются шестнадцатеричными числами. Данная система счисления имеет основание 16, соответственно и 16 различных символов. Первые десять символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 заимствованы из десятеричной системы. В качестве оставшихся шести символов применяются буквы A, B, C, D, E, F.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Высокая популярность шестнадцатеричной системы счисления поясняется тем, что при отображении одного и того же значения используется меньше разрядов по сравнению с десятичной системой и тем более с двоичной. Например, при отображении 100 используется три десятичных разряда 10010 или 7 двоичных разрядов 11001002 и только 2 шестнадцатеричных разряда 6416.
А если записать 1000000, то разница в количестве занимаемых разрядов буде еще более ощутима:
1 000 00010 = 1111 0100 0010 0100 00002 = F424016
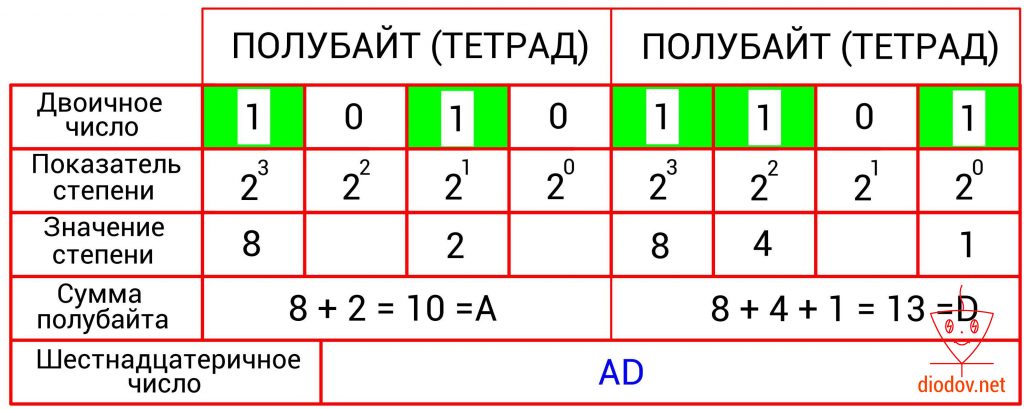
Преобразование двоичного числа в шестнадцатеричное
Еще одним положительным свойством шестнадцатеричного числа является простота получение его из двоичного. Такое преобразование выполняется следующим образом: сначала двоичное число разбивается на группы по четыре быта или на полубайты, которые еще называют тетрадами. Если количество битов не кратно четырем, то их дополняют нулями. Далее следует сложить значение всех битов в каждом полубайте. Сумма каждого полубайта даст значение отдельной цифры шестнадцатеричного числа.
Другие системы счисления
В цифровой технике также применяется восьмеричная система счисления, но она не нашла применения в микроконтроллерах.
Теоретические можно получить бесконечное значение систем счисления: троичную, пятиричную и даже сторичную, т.е. с любым основанием. Однако практической необходимости в этом пока что нет.
Наиболее простой и быстрый способ преобразования чисел с одной системы счисления в другую – это применение встроенного в операционную систему калькулятора. Найти его можно следующим образом: Пуск – Все программы – Стандартные – Калькулятор.
Чтобы перейти в «нужный» режим следует кликнуть по вкладке Вид и выбрать Программист или нажать комбинацию клавиш Alt+3.
В открывшемся окне можно вводить двоичные, восьмеричные, шестнадцатеричные и десятичные числа, выбрав соответствующий режим. Кроме того можно выполнять различные математические операции между ними.
В дальнейшем, при написании кода программы мы часто будем обращаться к данному калькулятору. Кроме того, опытные программисты любят использовать шестнадцатеричные числа, а нам проще будет понять двоичный код, поэтому калькулятор в помощь)
Битовые операции
Данный урок основан на оригинальном уроке по битовым операциям от Arduino, можете почитать его здесь – там всё описано чуть более подробно.
Двоичная система и хранение данных
| 2 в степени | DEC | BIN |
| 0 | 1 | 0b00000001 |
| 1 | 2 | 0b00000010 |
| 2 | 4 | 0b00000100 |
| 3 | 8 | 0b00001000 |
| 4 | 16 | 0b00010000 |
| 5 | 32 | 0b00100000 |
| 6 | 64 | 0b01000000 |
| 7 | 128 | 0b10000000 |
Таким образом, степень двойки явно “указывает” на номер бита в байте, считая справа налево (примечание: в других архитектурах может быть иначе). Напомню, что абсолютно неважно, в какой системе исчисления вы работаете – микроконтроллеру всё равно и он во всём видит единицы и нули. Если “сложить” полный байт в десятичном представлении битов, то мы получим как раз 255: 128+64+32+16+8+4+2+1 = 255. Нетрудно догадаться, что число 0b11000000 равно 128+64, то есть 192. Именно таким образом и получается весь диапазон от 0 до 255, который умещается в один байт. Если взять два байта – будет всё то же самое, просто ячеек будет 16, то же самое для 4 байт – 32 ячейки с единицами и нулями, каждая имеет свой номер согласно степени двойки. Давайте начнём манипуляции с битами с самого простого – с макро-функций, которые идут “в комплекте” с ядром Arduino.
Макросы для манипуляций с битами
В “библиотеке” Arduino.h есть несколько удобных макросов, которые позволяют включать и выключать биты в байте:
| Макросы Arduino.h | Действие |
| bitRead(value, bit) | Читает бит под номером bit в числе value |
| bitSet(value, bit) | Включает (ставит 1) бит под номером bit в числе value |
| bitClear(value, bit) | Выключает (ставит 0) бит под номером bit в числе value |
| bitWrite(value, bit, bitvalue) | Ставит бит под номером bit в состояние bitvalue (0 или 1) в числе value |
| bit(bit) | Возвращает 2 в степени bit |
| Другие встроенные макросы | |
| _BV(bit) | Возвращает 2 в степени bit |
| bit_is_set(value, bit) | Проверка на включенность (1) бита bit в числе value |
| bit_is_clear(value, bit) | Проверка на выключенность (0) бита bit в числе value |
Битовые операции
Переходим к более сложным вещам. На самом деле они максимально просты для микроконтроллера, настолько просты, что выполняются за один такт. При частоте 16 МГц (большинство плат Arduino) одна операция занимает 0.0625 микросекунды.
Битовое И
И (AND), оно же “логическое умножение”, выполняется оператором & или and и возвращает следующее:
Основное применение операции И – битовая маска. Позволяет “взять” из байта только указанные биты:
То есть при помощи & мы взяли из байта 0b11001100 только биты 10000111, а именно – 0b11001100, и получили 0b10000100 Также можно использовать составной оператор &=
Битовое ИЛИ
ИЛИ (OR), оно же “логическое сложение”, выполняется оператором | или or и возвращает следующее:
Основное применение операции ИЛИ – установка бита в байте:
Также можно использовать составной оператор |=
Вы уже поняли, что указывать на нужные биты можно любым удобным способом: в бинарном виде (0b00000001 – нулевой бит), в десятичном виде (16 – четвёртый бит) или при помощи макросов bit() или _BV() ( bit(7) даёт 128 или 0b10000000, _BV(7) делает то же самое)
Битовое НЕ
Битовая операция НЕ (NOT) выполняется оператором
и просто инвертирует бит:
Также она может инвертировать байт:
Битовое исключающее ИЛИ
Битовая операция исключающее ИЛИ (XOR) выполняется оператором ^ или xor и делает следующее:
Данная операция обычно используется для инвертирования состояния отдельного бита:
То есть мы взяли бит №7 в байте 0b11001100 и перевернули его в 0, получилось 0b01001100, остальные биты не трогали.
Битовый сдвиг
Битовый сдвиг делает не что иное, как умножает или делит байт на 2 в степени. Да, это операция деления, выполняющаяся за один такт процессора! К этому мы ещё вернёмся ниже. Посмотрите на работу оператора сдвига и сравните её с макросами bit() и _BV() :
Включаем-выключаем
Вспомним пример из пункта про битовое ИЛИ, про установку нужного бита. Вот эти варианты кода делают одно и то же:
Как насчёт установки нескольких бит сразу?
Или прицельного выключения бит? Тут чуть по-другому, используя &= и
Выключить несколько бит сразу? Пожалуйста!
Именно такие конструкции встречаются в коде высокого уровня и библиотеках, именно так производится работа с регистрами микроконтроллера. Вернёмся к устройству Ардуиновских макросов:
Я думаю, комментарии излишни: макросы состоят из тех же элементарных битовых операций и сдвигов!
Быстрые вычисления
Как я уже говорил, битовые операции – самые быстрые. Если требуется максимальная скорость вычислений – их можно оптимизировать и подогнать под “степени двойки”, но иногда компилятор делает это сам, подробнее смотри в уроке про оптимизацию кода. Рассмотрим базовые операции:
Примечание: рассмотренные выше операции работают только с целочисленными типами данных!
Экономия памяти
При помощи битовых операций можно экономить немного памяти, пакуя данные в блоки. Например, переменная типа boolean занимает в памяти 8 бит, хотя принимает только 0 и 1. В один байт можно запаковать 8 логических переменных, например вот так:
Ещё интересный пример сжатия
Таким образом мы отбросили у красного и синего младшие (правые) биты, в этом и заключается сжатие. Чем больше битов отброшено – тем менее точно получится “разжать” число. Например сжимали число 0b10101010 (170 в десятичной) на три бита, при сжатии получили 0b10101000, т.е. потеряли три младших бита, и в десятичной уже получится 168. Для упаковки используется битовый сдвиг и маска, таким образом мы берём первые пять битов красного, шесть зелёного и пять синего, и задвигаем на нужные места в результирующей 16-битной переменной. Всё, цвет сжат и его можно хранить. Для распаковки используется обратная операция: выбираем при помощи маски нужные биты и сдвигаем их обратно в байт:
Как и в примере со светодиодами, мы просто брали нужные биты ( в этом случае младшие два, 0b11 ) и сдвигали их на нужное расстояние. Для распаковки делаем в обратном порядке:
И получим обратно наши байты. Также маску можно заменить на более удобную для работы запись, задвинув 0b11 на нужное расстояние:
Ну и теперь, проследив закономерность, можно сделать для себя функцию или макрос чтения пакета:
Где x это пакет, а y – порядковый номер запакованного значения. Выведем посмотрим:
“Трюки” с битами
На битовых операциях можно сделать очень много всего интересного, и работать оно будет очень быстро и занимать мало места. Огромный список битовых трюков и хаков можно посмотреть в этой статье, их там очень много и все с примерами. Есть ещё один небольшой сборник самых простых и полезных хаков вот здесь (английский). Его я перевёл, смотрите ниже под спойлером. Другой вариант перевода (могут быть не все трюки) можно посмотреть здесь.
Перемотка бита
Целые
Установка n го бита
Выключение n го бита
Инверсия n го бита
Округление до ближайшей степени двойки
Округление вниз
Получение максимального целого
Получение минимального целого
Получение максимального long
Умножение на 2
Деление на 2
Умножение на m ую степень двойки
Деление на m ую степень двойки
Остаток от деления
Проверка равенства
Проверка на чётность (кратность 2)
Обмен значениями
Получение абсолютного значения
Максимум из двух
Минимум из двух
Проверка на одинаковый знак
Смена знака
Вернёт 2 n
Является ли число степенью 2
Остаток от деления на 2 n на m
Среднее арифметическое
Получить m ый бит из n (от младшего к старшему)
Получить m ый бит из n (от старшего к младшему)
Проверить включен ли n ый бит
Выделение самого правого включенного бита
Выделение самого правого выключенного бита
Выделение правого включенного бита
Выделение правого выключенного бита
n + 1
n – 1
Получение отрицательного значения
if (x == a) x = b; if (x == b) x = a;
Поменять смежные биты
Different rightmost bit of numbers m & n
Common rightmost bit of numbers m & n
Десятичные дроби
Примечание: хаки с float могут не работать на Ардуино! Разбить float в массив бит (unsigned uint32_t)
Вернуть массив бит обратно в float
Быстрый обратный квадратный корень
Быстрый n ый корень из целого числа
Быстрая степень
Быстрый натуральный логарифм
Быстрая экспонента
Строки
Конвертировать в нижний регистр
Конвертировать в верхний регистр
Инвертировать регистр
Позиция буквы в алфавите (англ)
Позиция большой буквы в алфавите (англ)
Позиция строчной буквы в алфавите (англ)
Другое
Быстрая конвертация цвета R5G5B5 в R8G8B8
Приоритет операций
Чтобы не плодить скобки, нужно знать приоритет операций. В C++ он такой: