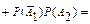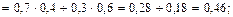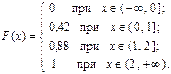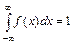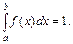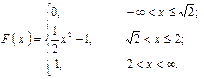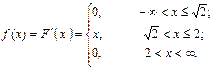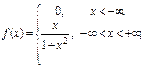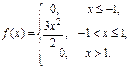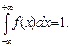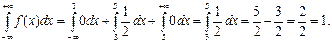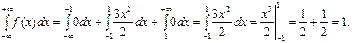какие значения принимает функция распределения f x
Какие значения принимает функция распределения f x
(F2) cХЭЕУФЧХАФ РТЕДЕМЩ Й ; (F3) ПОБ Ч МАВПК ФПЮЛЕ ОЕРТЕТЩЧОБ УМЕЧБ:
фПЮОП ФБЛ ЦЕ ДПЛБЦЕН ПУФБМШОЩЕ УЧПКУФЧБ.
(F4) ч МАВПК ФПЮЛЕ ТБЪОЙГБ ТБЧОБ :
(F5) дМС МАВПК УМХЮБКОПК ЧЕМЙЮЙОЩ ЙНЕЕФ НЕУФП ТБЧЕОУФЧП:
йЪ УЧПКУФЧ (F4) Й (F5) РПМХЮБЕН УМЕДХАЭЕЕ УЧПКУФЧП.
рПУЛПМШЛХ ЖХОЛГЙС ТБУРТЕДЕМЕОЙС ПДОПЪОБЮОП ПРТЕДЕМСЕФ ТБУРТЕДЕМЕОЙЕ УМХЮБКОПК ЧЕМЙЮЙОЩ ( ЬФХ ЖТБЪХ УФПЙФ ЛБЛ УМЕДХЕФ ПВДХНБФШ!), НПЦОП УЮЙФБФШ ЧПЪНПЦОПУФШ РТЕДУФБЧЙФШ ЖХОЛГЙА ТБУРТЕДЕМЕОЙС ЙОФЕЗТБМПН (14) ПФ ОЕПФТЙГБФЕМШОПК ЖХОЛГЙЙ ПРТЕДЕМЕОЙЕН БВУПМАФОП ОЕРТЕТЩЧОПЗП ТБУРТЕДЕМЕОЙС.
(f3) еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ БВУПМАФОП ОЕРТЕТЩЧОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ЕЈ ЖХОЛГЙС ТБУРТЕДЕМЕОЙС ЧУАДХ ОЕРТЕТЩЧОБ.
ьФПФ ЖБЛФ УМЕДХЕФ ЙЪ УЧПКУФЧБ 7 Й ЙЪ (F4). ъБНЕФЙН, ЮФП (f3) ЕУФШ ФБЛЦЕ УМЕДУФЧЙЕ РТЕДУФБЧМЕОЙС (14) Й ОЕРТЕТЩЧОПУФЙ ЙОФЕЗТБМБ ЛБЛ ЖХОЛГЙЙ ЧЕТИОЕЗП РТЕДЕМБ.
(f4) еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ БВУПМАФОП ОЕРТЕТЩЧОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ЕЈ ЖХОЛГЙС ТБУРТЕДЕМЕОЙС ДЙЖЖЕТЕОГЙТХЕНБ РПЮФЙ ЧУАДХ, Й
пРЙТБСУШ ОБ УЧПКУФЧБ (f4) Й (14), НПЦОП УЖПТНХМЙТПЧБФШ ФБЛПК ЛТЙФЕТЙК БВУПМАФОПК ОЕРТЕТЩЧОПУФЙ ТБУРТЕДЕМЕОЙС: ТБУРТЕДЕМЕОЙЕ У ЖХОЛГЙЕК ТБУРТЕДЕМЕОЙС БВУПМАФОП ОЕРТЕТЩЧОП, ЕУМЙ РТЙ ЧУЕИ ЙНЕЕФ НЕУФП ТБЧЕОУФЧП:
йЪ ПРТЕДЕМЕОЙС БВУПМАФОП ОЕРТЕТЩЧОПЗП ТБУРТЕДЕМЕОЙС Й УЧПКУФЧБ 7 УТБЪХ УМЕДХЕФ УЧПКУФЧП:
(f5) еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ БВУПМАФОП ОЕРТЕТЩЧОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ДМС МАВЩИ ЙНЕАФ НЕУФП ТБЧЕОУФЧБ:
рТЙНЕТПН ФБЛПК ЖХОЛГЙЙ ТБУРТЕДЕМЕОЙС УМХЦЙФ МЕУФОЙГБ лБОФПТБ:
Функция распределения



Универсальным способом задания закона распределения, пригодным как для дискретных, так и для непрерывных случайных величин, является функция распределения.
Функцией распределения случайной величины X называется функция F(x), определяющая для каждого значения x вероятность того, что случайная величина X примет значение меньшее, чем x, то есть
Функция распределения дискретных случайных величин может быть определена по формуле
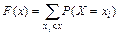
Если известен ряд распределения дискретной случайной величины, легко вычислить и построить ее функцию распределения. Продемонстрируем, как это делается на примере 23.
Пример 25. Вычислить и построить функцию распределения для дискретной случайной величины, закон распределения которой, имеет вид:
| xi | 0,1 | 1,2 | 2,3 | 4,5 |
| pi | 0,1 | 0,2 | 0,6 | 0,1 |
Решение. Определим значения функции F(x) = P(X
Из непрерывности функции F(x) следует, что вероятность каждого отдельного значения непрерывной случайной величины равна нулю.
Так как вероятность каждого отдельного значения непрерывной случайной величины равна 0, свойство 3 функции распределения для непрерывной случайной величины будет иметь вид
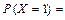
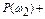
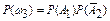
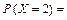
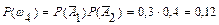
(Проверим, что 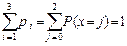
Ряд распределения данной случайной величины X имеет вид
| xi | Итого | ||
| pi | 0,42 | 0,46 | 0,12 |
Столбцовая диаграмма, соответствующая этому ряду распределения, приведена на рисунке 9.
Вычислим функцию распределения данной случайной величины:
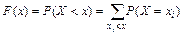
при x Î (- ¥, 0] 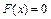
при x Î (0, 1] 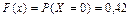
при x Î (1, 2] 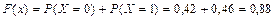
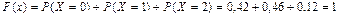
Итак, функция распределения рассматриваемой случайной величины имеет вид:
График функции F(x) приведён на рисунке 10.
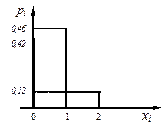 | 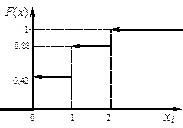 |
| Рисунок 9 – Столбцовая диаграмма | Рисунок 10 – Функция распределения |
Функция плотности распределения вероятностей непрерывной случайной величины.
Плотностью распределения вероятностей непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке:
По своему смыслу значения функции f(x) пропорциональны вероятности того, что исследуемая случайная величина примет значение где-то в непосредственной близости от точки x.
Функция плотности распределения f(x), как и функция распределения F(x), является одной из форм задания закона распределения, но она применима только для непрерывных случайных величин. Функцию плотности распределения вероятностей f(x) еще называют дифференциальной функцией распределения, тогда как функцию распределения F(x) называют, соответственно, интегральной функцией распределения.
График функции плотности распределения f(x) называется кривой распределения.
Рассмотрим свойства, которыми обладает функция плотности распределения непрерывной случайной величины.
Свойство 1. Плотность распределения вероятностей – неотрицательная функция:
(геометрически: кривая распределения лежит не ниже оси абсцисс).
Свойство 2. Вероятность попадания значения случайной величины на участок от a до b определяется по формуле
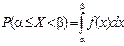
(геометрически: эта вероятность равна площади криволинейной трапеции, ограниченной кривой f(x), осью Ох и прямыми x = a и x = b).
Свойство 3.
(геометрически: площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице).
В частности, если все возможные значения случайной величины принадлежат отрезку [a, b], то
Свойство 4. Функция распределения F(x) может быть найдена по известной функции плотности распределения следующим образом:
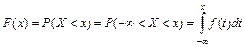
Пример 27. Непрерывная случайная величина задана функцией распределения
Определить дифференциальную функцию плотности распределения.
Решение. Определим дифференциальную функцию плотности распределения
Пример 28. Является ли плотностью распределения некоторой случайной величины каждая из следующих функций?
а) 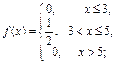
в)
Решение. а) Проверим справедливость свойства 3:
В данном случае имеем
Функция неотрицательна для всех x. То есть заданная функция является функцией плотности распределения некоторой случайной величины.
б) Заданная функция не является плотностью распределения некоторой случайной величины, так как 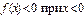
в) Проверим справедливость свойства 3:
В данном случае имеем
Функция неотрицательна для всех 
Вопросы для самоконтроля
1. Что называется случайной величиной?
2. Какие величины называются дискретными? непрерывными?
3. Что называется законом распределения случайной величины?
4. Какими способами может быть задан закон распределения дискретной случайной величины? непрерывной?
5. Что характеризует функция распределения F(x) случайной величины?
6. Как определить вероятность попадания значения случайной величины в некоторый интервал с помощью функции распределения?
7. Что характеризует функция плотности распределения случайной величины? Укажите ее вероятностный смысл.
8. Для каких величин определена функция плотности распределения?
9. Может ли функция плотности распределения принимать отрицательные значения?
10. Как связаны между собой функции F(x) и f(x)?
11. Какие случайные величины называются непрерывными?
12. Чему равна площадь фигуры, ограниченной кривой распределения и осью абсцисс?
13. Как определить вероятность попадания значения непрерывной случайной величины в некоторый интервал с помощью функции плотности распределения?
Непрерывная случайная величина, функция распределения и плотность вероятности
Определение непрерывной случайной величины и её связь с вероятностью
Случайной величиной называется переменная, которая может принимать те или иные значения в зависимости от различных обстоятельств, и случайная величина называется непрерывной, если она может принимать любое значение из какого-либо ограниченного или неограниченного интервала. Для непрерывной случайной величины невозможно указать все возможные значения, поэтому обозначают интервалы этих значений, которые связаны с определёнными вероятностями.
Примерами непрерывных случайных величин могут служить: диаметр детали, обтачиваемой до заданного размера, рост человека, дальность полёта снаряда и др.
Так как для непрерывных случайных величин функция F(x), в отличие от дискретных случайных величин, нигде не имеет скачков, то вероятность любого отдельного значения непрерывной случайной величины равна нулю.
Функция распределения непрерывной случайной величины и плотность вероятности
В качестве закона распределения, имеющего смысл только для непрерывных случайных величин, вводится понятие плотности распределения или плотности вероятности. Подойдём к нему путём сравнения смысла функции распределения для непрерывной случайной величины и для дискретной случайной величины.
Итак, функцией распределения случайной величины (как дискретной, так и непрерывной) или интегральной функцией называется функция 
Плотностью вероятности f(x) непрерывной случайной величины называется производная её функции распределения:

Зная функцию плотности, можно найти вероятность того, что значение непрерывной случайной величины принадлежит закрытому интервалу [a; b]:
вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала [a; b], равна определённому интегралу от её плотности вероятности в пределах от a до b:

При этом общая формула функции F(x) распределения вероятностей непрерывной случайной величины, которой можно пользоваться, если известна функция плотности f(x) :

График плотности вероятности непрерывной случайной величины называется её кривой распределения (рис. ниже).
Площадь фигуры (на рисунке заштрихована), ограниченной кривой, прямыми, проведёнными из точек a и b перпендикулярно оси абсцисс, и осью Ох, графически отображает вероятность того, что значение непрерывной случайной величины Х находится в пределах от a до b.
Свойства функции плотности вероятности непрерывной случайной величины
1. Вероятность того, что случайная величина примет какое-либо значение из интервала 
2. Функция плотности вероятности не может принимать отрицательные значения:

а за пределами существования распределения её значение равно нулю
Плотность распределения f(x), как и функция распределения F(x), является одной из форм закона распределения, но в отличие от функции распределения, она не универсальна: плотность распределения существует только для непрерывных случайных величин.
Упомянем о двух важнейших в практике видах распределения непрерывной случайной величины.
Если функция плотности распределения f(x) непрерывной случайной величины в некотором конечном интервале [a; b] принимает постоянное значение C, а за пределами интервала принимает значение, равное нулю, то такое распределение называется равномерным.
Если график функции плотности распределения симметричен относительно центра, средние значения сосредоточены вблизи центра, а при отдалении от центра собираются более отличающиеся от средних (график функции напоминает разрез колокола), то такое распределение называется нормальным.
Пример 1. Известна функция распределения вероятностей непрерывной случайной величины:
Найти функцию f(x) плотности вероятности непрерывной случайной величины. Построить графики обеих функций. Найти вероятность того, что непрерывная случайная величина примет какое-либо значение в интервале от 4 до 8: 
Решение. Функцию плотности вероятности получаем, находя производную функции распределения вероятностей:
Найдём вероятность того, что непрерывная случайная величина примет какое либо значение в интервале от 4 до 8:

Пример 2. Функция плотности вероятности непрерывной случайной величины дана в виде:
Решение. Коэффициент C найдём, пользуясь свойством 1 функции плотности вероятности:
Таким образом, функция плотности вероятности непрерывной случайной величины:

Таким образом, полная запись функции распределения вероятностей:
Найдём вероятность того, что непрерывная случайная величина примет какое либо значение в интервале от 0 до 5:

Пример 3. Плотность вероятности непрерывной случайной величины X задана равенством 

Решение. По условию 

Следовательно, 


Теперь находим вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала ]0, 5[:
Теперь получим функцию распределения данной случайной величины:
Пример 4. Найти плотность вероятности непрерывной случайной величины X, которая принимает только неотрицательные значения, а её функция распределения 
Решение. По определению плотности вероятности получаем
при 


Пример 5. Плотность распределения непрерывной случайной величины задана формулой:

1) найти функцию распределения непрерывной случайной величины;
2) найти вероятность того, что непрерывная случайная величина примет значение, лежащее между 1 и 2.
2) вероятность попадания непрерывной случайной величины на участок между 1 и 2 вычислим как приращение функции распределения на этом участке:
Пример 6. Непрерывная случайная величина имеет плотность


1) найти вероятность попадания непрерывной случайной величины на участок от 0 до π/4;
2) функцию распределения непрерывной случайной величины.
1) находим вероятность:

2) находим функцию распределения непрерывной случайной величины:
Пример 7. Плотность распределения непрерывной случайной величины задана формулой

Найти вероятность попадания непрерывной случайной величины на участок (-1; +1)