какие знаки операций употребляются в формулах что может быть операндом назначение скобок
Выражения, операнды и операторы
Многие сегодня хотят стать программистами. Хотят. Но ничего не делают для этого. Не делают даже простых вещей. Не хотят даже прочитать книжку из 10 страниц. В итоге так и остаются никем. Потому что мечты не сбываются никогда. Сбываются только планы… Подробнее.
Итак, начнём с выражений.
Это выражение, которое записывает в переменную х число 100.
Когда вы будете создавать выражения, не забывайте, что типы операндов в выражении должны совпадать. Например, такой код
вызовет ошибку во время компиляции, и программа не будет создана. Все похожие типы (например, все целочисленные) можно использовать в качестве операндов. Например, такой код
Не вызовет особых возражений у компилятора, однако это может повлечь за собой неприятности, которые были описаны ранее.
Основные виды операторов: арифметические, операторы присваивания, сравнения, логические и поразрядные (побитовые).
Также разделяются операторы по количеству операндов:
Попробуйте догадаться, какие из приведённых ниже операторов являются унарными, а какие бинарными:
Если вы думаете, что на этом с операторами всё, то вы заблуждаетесь. Мы ещё долго и нудно будем о них говорить, так как это тема большая и очень важная.
Оператор + выполняет операцию сложения
Оператор * выполняет операцию умножения
Домашнее задание придумайте сами. У вас пока недостаточно знаний об операторах и выражениях, чтобы грамотно использовать их в своих программах.
Выражения, операнды, операции



Тема 11
При выполнении программы осуществляется обработка данных, в ходе которой с помощью выражений вычисляются и используются различные значения. Выражение представляет собой конструкцию, определяющую состав данных, операции и порядок выполнения операций над данными. Выражение состоит из операндов, знаков операций и круглых скобок. В простейшем случае выражение может состоять из одной переменной или константы. Тип значения выражения определяется типом операндов и составом выполняемых операций.
Операнды представляют собой данные, над которыми выполняются действия. В качестве операндов могут использоваться константы, переменные, элементы массивов и функции.
Операции – это действия, которые выполняются над операндами. Операции бываю унарными и бинарными. Унарная операция относится к одному операнду, и ее знак записывается перед операндом, например, — x. Бинарная операция выражает отношение между двумя операндами, и знак ее записывается между операндами, например, x + y.
Круглые скобки используются для указания порядка выполнения операций.
Если в операциях используется несколько данных, то их типы должны быть либо идентичными, либо совместимыми.
В зависимости от типов операций и операндов выражения могут быть арифметическими, логическими и строковыми.
Арифметические выражения (АВ). Результатом выполнения АВ является число, тип которого зависит от типов операндов, составляющих это выражение. В АВ можно использовать числовые типы (целочисленные и вещественные), арифметические операции и функции, возвращающие числовое значение.
Тип значения АВ определяется типом операндов и операциями. Если в операции участвуют целочисленные операнды, то результат операции также будет целочисленного типа. Если хотя бы один из операндов принадлежит к вещественному типу, то результат также будет вещественным. Исключением является операция деления, результат которой всегда вещественный.
Унарные арифметические операции + (Сохранение знака) и –(Отрицание знака) относятся к знаку числа и не меняют типа числа.
Примеры. Пусть в программе есть строки:
var a, b, c, d: integer; x, y: real;
c:= a div b; d:= a mod b; //c=3, d=1
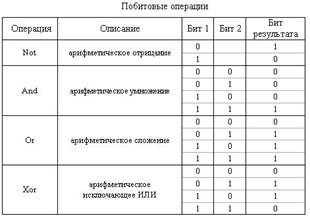
Над данными целочисленного типа можно выполнять также следующие побитовые (поразрядные) операции:
o Shl– сдвиг влево;
o Shr– сдвиг вправо;
o And– И (арифметическое умножение);
o Or– ИЛИ (арифметическое сложение);
o Xor– арифметическое исключающее ИЛИ;
o Not– Не (арифметическое отрицание).
Особенностью побитовых операций является то, что они выполняются над операндами поразрядно.
Примеры. Пусть в программе есть строки:
var a, b, c, d: integer;
c:= Not a; // a= 0101, Not (0101) = 1010 =10 дес .
d:= a And b; // b=1001, 0101 And 1001 = 0001 = 1 дес .
Логические выражения (ЛВ). Результатом выполнения ЛВ является логическое значение Trueили False. Такие выражения чаще всего используются в условных операторах и операторах цикла. Логические выражения могут содержать:
o логические константы Trueи False;
o логические переменные типа Boolean;
o операции сравнения (отношения);
o логические операции;
Результат выполнения логических операций при применении их к логическим выражениям (операндам логического типа) будет логического типа (Boolean). Логические операции And, Or, Xor являются бинарными, операция Not– унарной.
Какие знаки операций употребляются в формулах что может быть операндом назначение скобок
=F7*С14+B12
Формула состоит из трех операндов (аргументов), которые разделены математическими операторами умножения и сложения. Аргументы представлены ссылками на ячейки электронной таблицы.
=ПРОИЗВЕД(А1:А6)+3
=15+2*0,2-10
В формуле 4 аргумента, представленных константами. Три математических оператора: сложение, умножение, вычитание
=А15*3+2*6
Константы – текстовые или числовые значения, которые вводятся в ячейку и не могут изменяться во время вычислений
Пример:
Ссылка на ячейку или группу ячеек – способ, которым указывается конкретная ячейка или несколько ячеек.
Пример:
Ссылка на отдельную ячейку является ее координатой.
Значение пустой ячейки равно 0.
Ссылки на ячейки бывают двух типов:
При копировании формул относительные ссылки изменяются на размер перемещения!
Операторами обозначаются операции, которые следует выполнить над операндами формулы
В Microsoft Excel включено четыре вида операторов:
Служат для выполнения арифметических операций, таких как сложение, вычитание, умножение
Арифметические операции выполняются над числами!
Используются арифметические операторы:
Используются для сравнения двух значений. Результатом сравнения является логическое значение: либо ИСТИНА, либо ЛОЖЬ.
Для описания ссылок на диапазоны ячеек
Для объединения нескольких текстовых строк в одну
Повышение приоритета операций нужно для обеспечения правильности вычислений.
Для повышения приоритета операции используют круглые скобки
Допустим, необходимо составить формулу для вычисления выражения, представленного в виде дроби:
Правильный результат достигается только в третьем случае. Числитель делится на знаменатель.
Если формула в ячейке не может быть правильно вычислена, Microsoft Excel выводит в ячейку сообщение об ошибке
Если формула содержит ссылку на ячейку, которая содержит значения ошибки, то вместо этой формулы также будет выводиться сообщение об ошибке
#### – ширина ячейки не позволяет отобразить число в заданном формате;
#ИМЯ? – Microsoft Excel не смог распознать имя, использованное в формуле;
#ДЕЛ/0! – в формуле делается попытка деления на нуль;
#ЧИСЛО! – нарушены правила задания операторов, принятые в математике;
#Н/Д – такое сообщение может появиться, если в качестве аргумента задана ссылка на пустую ячейку;
#ПУСТО! – неверно указано пересечение двух областей, которые не имеют общих ячеек;
#ССЫЛКА! – в формуле задана ссылка на несуществующую ячейку;
#ЗНАЧ! – использован недопустимый тип аргумента.
Электроника для всех
Блог о электронике
1.3.1. Операнды и операции
Комбинация знаков операций и операндов, результатом которой является определенное значение, называется выражением. Знаки операций определяют действия, которые должны быть выполнены над операндами. Каждый операнд в выражении может быть выражением. Значение выражения зависит от расположения знаков операций и круглых скобок в выражении, а также от приоритета выполнения операций.
В языке СИ присваивание также является выражением, и значением такого выражения является величина, которая присваивается.
При вычислении выражений тип каждого операнда может быть преобразован к другому типу. Преобразования типов могут быть неявными, при выполнении операций и вызовов функций, или явными, при выполнении операций приведения типов.
Операнд — это константа, литерал, идентификатор, вызов функции, индексное выражение, выражение выбора элемента или более сложное выражение, сформированное комбинацией операндов, знаков операций и круглых скобок. Любой операнд, который имеет константное значение, называется константным выражением. Каждый операнд имеет тип.
Если в качестве операнда используется константа, то ему соответствует значение и тип представляющей его константы. Целая константа может быть типа int, long, unsigned int, unsigned long, в зависимости от ее значения и от формы записи. Символьная константа имеет тип int. Константа с плавающей точкой всегда имеет тип double.
Строковый литерал состоит из последовательности символов, заключенных в кавычки, и представляется в памяти как массив элементов типа char, инициализируемый указанной последовательностью символов. Значением строкового литерала является адрес первого элемента строки и синтаксически строковый литерал является немодифицируемым указателем на тип char. Строковые литералы могут быть использованы в качестве операндов в выражениях, допускающих величины типа указателей. Однако так как строки не являются переменными, их нельзя использовать в левой части операции присваивания.
Следует помнить, что последним символом строки всегда является нулевой символ, который автоматически добавляется при хранении строки в памяти.
Идентификаторы переменных и функций. Каждый идентификатор имеет тип, который устанавливается при его объявлении. Значение идентификатора зависит от типа следующим образом:
Вызов функций состоит из выражения, за которым следует необязательный список выражений в круглых скобках:
выражение-1 ([ список выражений ])
Значением выражения-1 должен быть адрес функции (например, идентификатор функции). Значения каждого выражения из списка выражений передается в функцию в качестве фактического аргумента. Операнд, являющийся вызовом функции, имеет тип и значение возвращаемого функцией значения.
Индексное выражение задает элемент массива и имеет вид:
Тип индексного выражения является типом элементов массива, а значение представляет величину, адрес которой вычисляется с помощью значений выражение-1 и выражение-2.
Обычно выражение-1 — это указатель, например, идентификатор массива, а выражение-2 — это целая величина. Однако требуется только, чтобы одно из выражений было указателем, а второе целочисленной величиной. Поэтому выражение-1 может быть целочисленной величиной, а выражение-2 указателем. В любом случае выражение-2 должно быть заключено в квадратные скобки. Хотя индексное выражение обычно используется для ссылок на элементы массива, тем не менее индекс может появляться с любым указателем.
Индексные выражения для ссылки на элементы одномерного массива вычисляются путем сложения целой величины со значениями указателя с последующим применением к результату операции разадресации (*).
Так как одно из выражений, указанных в индексном выражении, является указателем, то при сложении используются правила адресной арифметики, согласно которым целая величина преобразуется к адресному представлению, путем умножения ее на размер типа, адресуемого указателем. Пусть, например, идентификатор arr объявлен как массив элементов типа double.
Таким образом, чтобы получить доступ к i-тому элементу массива arr можно написать аrr[i], что, в силу сказанного выше, эквивалентно i[a]. При этом величина i умножается на размер типа double и представляет собой адрес i-го элемента массива arr от его начала. Затем это значение складывается со значением указателя arr, что в свою очередь дает адрес i-го элемента массива. К полученному адресу применяется операция разадресации, т.е. осуществляется выборка элемента массива arr по сформированному адресу.
Таким образом, результатом индексного выражения arr[i] (или i[arr]) является значение i-го элемента массива.
Выражение с несколькими индексами ссылается на элементы многомерных массивов. Многомерный массив — это массив, элементами которого являются массивы. Например, первым элементом трехмерного массива является массив с двумя измерениями.
Для ссылки на элемент многомерного массива индексное выражение должно иметь несколько индексов заключенных к квадратные скобки:
выражение-1 [ выражение-2 ][ выражение-3 ] …
Такое индексное выражение интерпретируется слева направо, т.е. вначале рассматривается первое индексное выражение:
Результат этого выражения есть адресное выражение, с которым складывается выражение-3 и т.д. Операция разадресации осуществляется после вычисления последнего индексного выражения. Отметим, что операция разадресации не применяется, если значение последнего указателя адресует величину типа массива.
Рассмотрим процесс вычисления индексного выражения mass[1][2][2].
Если было бы указано mass [1][2], то результатом был бы указатель на массив из трех элементов типа int. Соответственно значением индексного выражения mass [1] является указатель на двухмерный массив.
Выражение выбора элемента применяется, если в качестве операнда надо использовать элемент структуры или объединения. Такое выражение имеет значение и тип выбранного элемента. Рассмотрим две формы выражения выбора элемента:
В первой форме выражение представляет величину типа struct или union, а идентификатор — это имя элемента структуры или объединения. Во второй форме выражение должно иметь значение адреса структуры или объединения, а идентификатор — именем выбираемого элемента структуры или объединения.
Обе формы выражения выбора элемента дают одинаковый результат. Действительно, запись, включающая знак операции выбора (->), является сокращенной версией записи с точкой для случая, когда выражению стоящему перед точкой предшествует операция разадресации (*), примененная к указателю, т.е. запись
в случае, если выражение является указателем.
В приведенном примере используется операция выбора (.) для доступа к элементу left структурной переменной elem. Таким образом элементу left структурной переменной elem присваивается адрес самой переменной elem, т.е. переменная elem хранит ссылку на себя саму.
Приведение типов это изменение (преобразование) типа объекта. Для выполнения преобразования необходимо перед объектом записать в скобках нужный тип:
( имя-типа ) операнд.
Приведение типов используются для преобразования объектов одного скалярного типа в другой скалярный тип. Однако выражению с приведением типа не может быть присвоено другое значение.
int i; bouble x; b = (double)i+2.0;
В этом примере целая переменная i с помощью операции приведения типов приводится к плавающему типу, а затем уже участвует в вычислении выражения.
Константное выражение — это выражение, результатом которого является константа. Операндом константного выражения могут быть целые константы, символьные константы, константы с плавающей точкой, константы перечисления, выражения приведения типов, выражения с операцией sizeof и другие константные выражения. Однако на использование знаков операций в константных выражениях налагаются следующие ограничения:
Выражения со знаками операций могут участвовать в выражениях как операнды. Выражения со знаками операций могут быть унарными (с одним операндом), бинарными (с двумя операндами) и тернарными (с тремя операндами).
Унарное выражение состоит из операнда и предшествующего ему знаку унарной операции и имеет следующий формат:
Операции. По количеству операндов, участвующих в операции, операции подразделяются на унарные, бинарные и тернарные.
В языке Си имеются следующие унарные операции:
Унарные операции выполняются справа налево.
Операции увеличения и уменьшения увеличивают или уменьшают значение операнда на единицу и могут быть записаны как справа так и слева от операнда. Если знак операции записан перед операндом (префиксная форма), то изменение операнда происходит до его использования в выражении. Если знак операции записан после операнда (постфиксная форма), то операнд вначале используется в выражении, а затем происходит его изменение.
В отличие от унарных, бинарные операции, список которых приведен в табл.7, выполняются слева направо.
Таблица 7
| Знак операции | Операция | Группа операций |
|---|---|---|
| * | Умножение | Мультипликативные |
| / | Деление | |
| % | Остаток от деления | |
| + | Сложение | Аддитивные |
| — | Вычитание | |
| > | Сдвиг вправо | |
| = | Больше или равно | |
| == | Равно | |
| != | Не равно | |
| & | Поразрядное И | Поразрядные операции |
| | | Поразрядное ИЛИ | |
| ^ | Поразрядное исключающее ИЛИ | |
| && | Логическое И | Логические операции |
| || | Логическое ИЛИ | |
| , | Последовательное вычисление | Последовательного вычисления |
| = | Присваивание | Операции присваивания |
| *= | Умножение с присваиванием | |
| /= | Деление с присваиванием | |
| %= | Остаток от деления с присваиванием | |
| -= | Вычитание с присваиванием | |
| += | Сложение с присваиванием | |
| >= | Сдвиг вправо присваиванием | |
| &= | Поразрядное И с присваиванием | |
| |= | Поразрядное ИЛИ с присваиванием | |
| ^= | Поразрядное исключающее ИЛИ с присваиванием |
Левый операнд операции присваивания должен быть выражением, ссылающимся на область памяти (но не объектом объявленным с ключевым словом const), такие выражения называются леводопустимыми к ним относятся:
При записи выражений следует помнить, что символы (*), (&), (!), (+) могут\ обозначать унарную или бинарную операцию.
Добавить комментарий Отменить ответ
Этот сайт использует Akismet для борьбы со спамом. Узнайте как обрабатываются ваши данные комментариев.
Какие знаки операций употребляются в формулах что может быть операндом назначение скобок
Во всех языках программирования под выражением подразумевается конструкция, составленная из констант, переменных, знаков операций, функций, скобок. Выражение определяет порядок вычисления некоторого значения. Если это числовое значение, то такое выражение называют арифметическим. Вот несколько примеров арифметических выражений, записанных по правилам языка Си:
Три первых выражения имеют традиционную форму для языков программирования высокого уровня, поэтому их смысл очевиден. Следующие четыре выражения специфичны для языка Си.
Опишем набор операций, используемых в Си, а также правила записи и вычисления выражений. Напомним, что операция, применяемая к одному операнду, называется унарной, а операция с двумя операндами — бинарной.
— вычитание или унарный минус;
+ сложение или унарный плюс;
++ унарная операция увеличения на единицу (инкремент);
Все операции, кроме деления по модулю, применимы к любым числовым типам данных. Операция % применима только к целым числам.
Если хотя бы один из операндов имеет вещественный тип, то и результат будет вещественным. Например, операции 5./3, 5./3., 5/3. дадут вещественный результат 1.6666.
Различие проявляется при использовании префиксной и постфиксной форм в выражениях. Проиллюстрируем это на примерах. Первый пример:
В результате выполнения переменные получат следующие значения: а = 4, b = 3, с= 6. Второй пример:
Результаты будут такими: а = 4, b = 3, с=12.
По убыванию старшинства арифметические операции расположены в следующем порядке:
Одинаковые по старшинству операции выполняются в порядке слева направо. Д ля изменения порядка выполнения операций в выражениях могут применяться круглые скобки.
>= больше или равно, равно,
Как уже говорилось раньше, в стандарте Си нет логического типа данных. Поэтому результатом операции отношения является целое число: если отношение истинно — то 1, если ложно — то 0.
Результатом второго и третьего отношений будет 0 — ложь; результат четвертого отношения равен 1 — истина; результат первого отношения зависит от значения переменной а.
! операция отрицания (НЕ),
&& конъюнкция, логическое умножение (И),
| | дизъюнкция, логическое сложение (ИЛИ).
Например, логическое выражение, соответствующее системе неравенств 0 x
Обратите внимание на то обстоятельство, что здесь не понадобились круглые скобки для выделения операций отношения. В Си операции отношения старше конъюнкции и дизъюнкции. По убыванию приоритета логические операции и операции отношения расположены в следующем порядке:
Помимо рассмотренных в Си имеются поразрядные логические операции. Эти операции выполняются над каждой парой соответствующих двоичных разрядов внутреннего представления операндов. Их еще называют битовыми логическими операциями. Знаки битовых логических операций:
& поразрядная конъюнкция (И),
| поразрядная дизъюнкция (ИЛИ),
^ поразрядное исключающее ИЛИ,
поразрядное отрицание (НЕ).
Битовые логические операции вместе с операциями поразрядного сдвига влево ( >) позволяют добраться до каждого бита внутреннего кода. Чаще всего такие действия приходится выполнять в системных программах.
Операция присваивания. Знак операции присваивания =. Следствием отмеченного факта является то, что присваивание, как любой другой знак операции, может несколько раз входить в выражение. Например:
Присваивание имеет самый низкий приоритет (ниже только у операции «запятая»). Кроме того, операция присваивания — правоассоциативная. Это значит, что несколько подряд расположенных присваиваний выполняются справа налево. Поэтому в приведенном выше выражении первой выполнится операция сложения, затем переменной с присвоится значение суммы, затем это значение присвоится переменной b и в конце — переменной а.
а+=2 эквивалентно а=а+2,
х-=а+ b эквивалентно х=х-(а+ b ),
р/=10 эквивалентно р=р/10,
m*=n эквивалентно m=m*n,
г%=5 эквивалентно г=г%5.
Заметим, что вместо выражения а=а+2 предпочтительнее писать в программе а+=2, поскольку второе выражение будет вычисляться быстрее.
Операция явного преобразования типа (операция «тип»). Применение этой операции имеет следующий формат:
Операндом могут быть константа, переменная, выражение. В результате значение операнда преобразуется к указанному типу. Примеры использования преобразования типа:
По поводу последнего выражения заметим, что приоритет операции «тип» выше деления (и других бинарных арифметических операций), поэтому сначала значение переменной х приведется к целому типу (отбросится дробная часть), а затем выполнится деление по модулю.
Следующий фрагмент программы иллюстрирует одну из практических ситуаций, в которой потребовалось использовать преобразование типа:
В результате переменная с получит значение 0,5. Без преобразования типа ее значение стало бы равно 0.
sizeof (тип) и sizeof (выражение)
Результатом операции является целое число, равное количеству байтов, которое занимает в памяти величина явно указанного типа или величина, полученная в результате вычисления выражения. Последняя определяется также по типу результата выражения. Хотя по форме записи это похоже на функцию, однако sizeof является именно операцией. Ее приоритет выше, чем у бинарных арифметических операций, логических операций и отношений. Примеры использования операции:
sizeof (int) результат — 2
sizeof (1) результат — 2
sizeof (0.1) результат — 8
sizeof (1L) результат — 4
sizeof (char) результат — 1
sizeof (‘ a’) результат — 2
Операция «запятая». Эта необычная операция используется для связывания нескольких выражений в одно. Несколько выражений, разделенных запятыми, вычисляются последовательно слева направо. В качестве результата такого совмещенного выражения принимается значение самого правого выражения. Например, если переменная х имеет тип int, то значение выражения (х=3, 5*х) будет равно 15, а переменная х примет значение 3.
Данная операция реализует алгоритмическую структуру ветвления. Алгоритм ее выполнения следующий: первым вычисляется значение выражения 1, которое обычно представляет собой некоторое условие. Если оно истинно, т.е. не равно 0, то вычисляется выражение 2 и полученный результат становится результатом операции. В противном случае в качестве результата берется значение выражения 3.
Пример 1. Вычисление абсолютной величины переменной X можно организовать с помощью одной операции:
Пример 2. Выбор большего значения из двух переменных аи Ь:
Пример 3. Заменить большее значение из двух переменных аи b на единицу:
Правила языка в данном случае позволяют ставить условную операцию слева от знака присваивания.
Операции ( ) и [ ]. В языке Си круглые и квадратные скобки рассматриваются как операции, причем эти операции имеют наивысший приоритет. Их смысл будет раскрыт позже.
Подведем итог всему разговору об операциях Си/Си++, сведя их в общую табл. 2 и расположив по рангам. Ранг операции — это порядковый помер в ряду приоритетов. Чем больше ранг, тем ниже приоритет. В таблице отражено еще одно свойство операций — ассоциативность. Если одна и та же операция, повторяющаяся в выражении несколько раз, выполняется в порядке расположения слева направо, то она называется левоассоциа-тивной; если выполняется справа налево, то операция правоассоциативная. В таблице эти свойства отображены стрелками влево и вправо. Некоторые операции, присутствующие в таблице, пока не обсуждались.