подобрать параметры p q арима
ARIMA: строим прогноз на основе истории
Задача с тремя переменными
Для начала давайте рассмотрим три составляющие модели более подробно. Авторегрессия – модель временных рядов, в которой значение временного ряда в данный момент времени может быть выражено в виде линейной комбинации предыдущих значений этого же ряда и случайной ошибки, обладающей свойством «белого шума».
Процесс скользящего среднего – текущее значение случайного процесса представляется в виде линейной комбинации текущего и прошлых значений ошибки, по своим свойствам соответствующей «белому шуму».
Интегрированная составляющая отвечает за порядок дифференциации ряда при необходимости привести ряд к стационарному. Обычно рассчитывают разницу до 2-го порядка.
Главной задачей аналитика является определение значений данных параметров. Предлагаем рассмотреть на примере определение значений параметров p, d, q. Для применения модели ARIMA необходимо иметь данные в разрезе времени любого уровня динамики (годы, месяцы, дни и т.д.). Это могут быть продажи какого-либо товара, количество заказов, клиентов и т.д.
После построения модели получится прогноз по выбранному показателю. Построенный прогноз в дальнейшем может быть использован для принятия каких-либо управленческих решений или может стать входной информацией для формирования автоматического заказа на закупку товара.
Строим прогноз с помощью Prognoz Platform
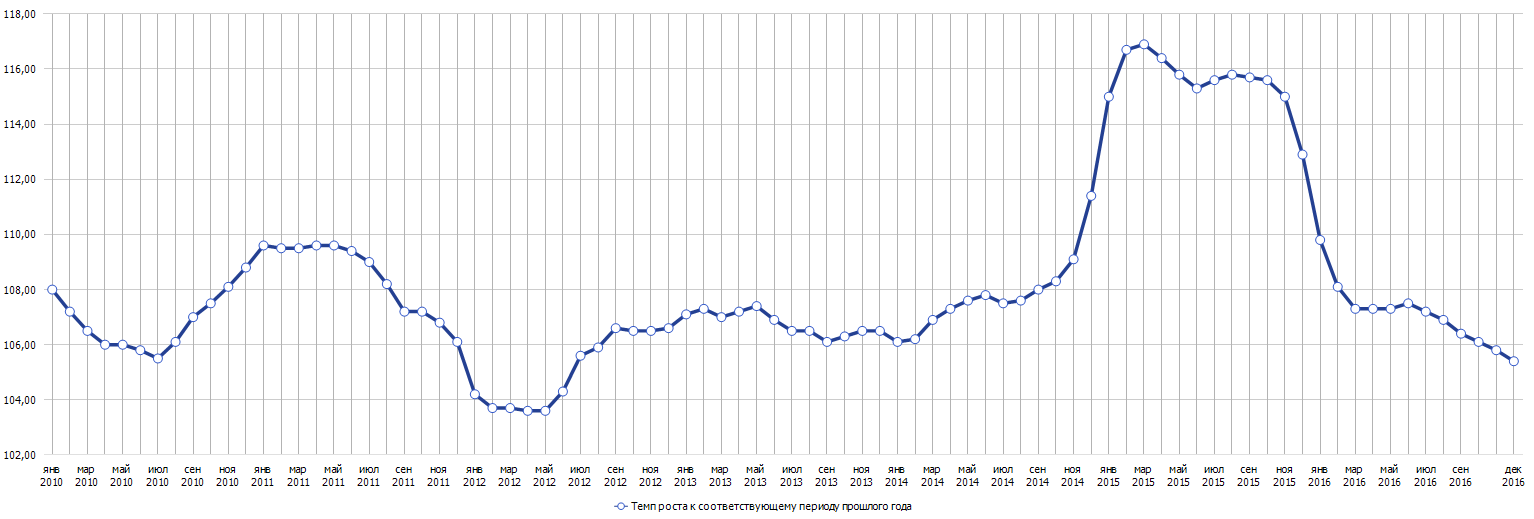
Рассмотрим данные по показателю «Индекс потребительских цен, к соответствующему периоду 2017 года по Российской Федерации». Данный показатель обычно называют инфляцией. Динамика исследуемого ряда приведена на рисунке ниже.
Для анализа ряда и построения ARIMA модели воспользуемся инструментом моделирования Prognoz Platform, который называется «Контейнер моделирования». Данный инструмент удобен тем, что одновременно позволяет увидеть все необходимые характеристики для построения ARIMA модели в одном окне, автоматически перестраивает модель при изменении её параметров и строит прогноз.
Также стоит отметить возможность применять преобразования к исследуемому ряду. Контейнер моделирования имеет интуитивно понятный интерфейс и позволяет строить модели без написания какого-либо кода.
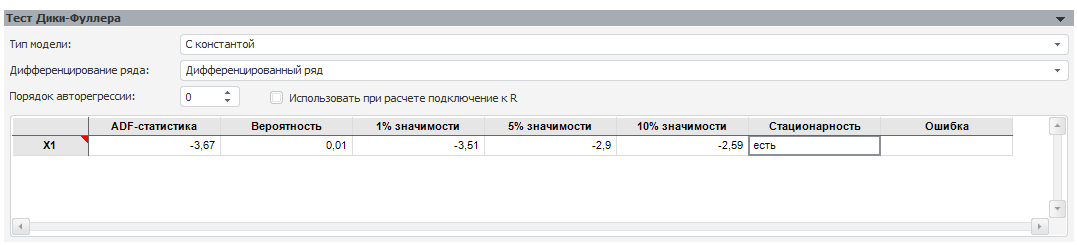
Первым параметром для оценки является параметр d. Для того чтобы определить, какое значение должен принимать этот параметр, необходимо провести для ряда тест Дики-Фулера. Данный тест можно найти в меню «Анализ» Prognoz Platform, пункт «Описательные статистики».
У данного теста есть два параметра:
Тип модели необходимо установить тот, который будет строиться для ряда. Мы будем строить модели с константой, поэтому выбираем пункт «С константой».
Результаты теста смотрите ниже.
Для того чтобы выбрать параметры p, q, можно воспользоваться автокорреляционной функцией и частной автокорреляционной функцией.
Под стационарным рядом понимается временной ряд, который стабилен во времени (его среднее и прочие характеристики с течением времени не изменяются).
Таким образом, инфляция во времени оказалась нестабильна (у неё изменяются среднее и другие характеристики), а это означает, что её достаточно трудно предсказывать, и выбранный метод ARIMA может не сработать. Для этого необходимо привести ряд к стабильному состоянию, например, рассчитав разности ряда. Разность ряда рассчитывается следующим образом: из текущего года вычитаем предыдущий год.
А есть ли тренд?
Частная автокорреляционная функция (ЧАКФ) – это зависимость частных коэффициентов автокорреляции от лага.
Рассмотрим графики АКФ и ЧАКФ для выбранного ряда. В «Контейнере моделирования» посмотреть графики данных функций можно в двух местах:
— При выборе модели ARIMA автоматически строятся данные функции.
— На вкладке «Анализ» – «Описательные статистики» – «Набор тестов». В «Наборе тестов» необходимо выбрать АКФ и ЧАКФ.
Анализируя графики функций, можно сделать вывод о наличии тренда, сезонности в ряде, а также выделить порядок авторегрессора и скользящего среднего.
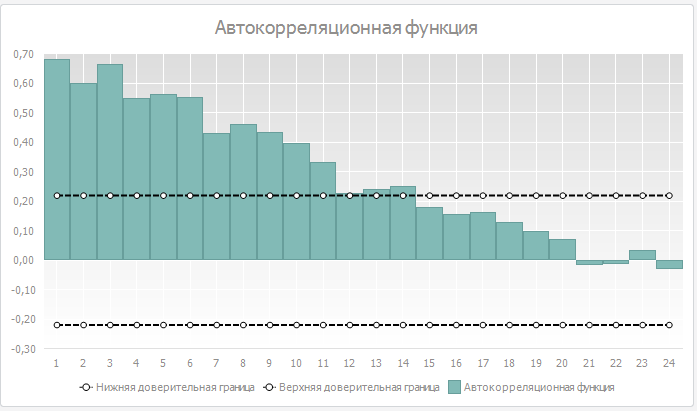
Если график АКФ сходится к нулю достаточно медленно, значит, в ряду присутствует тренд. Пример расположен ниже.
Если график сходится к нулю достаточно быстро и колеблется около него, то говорят, что присутствует процесс чистой автокорреляции.
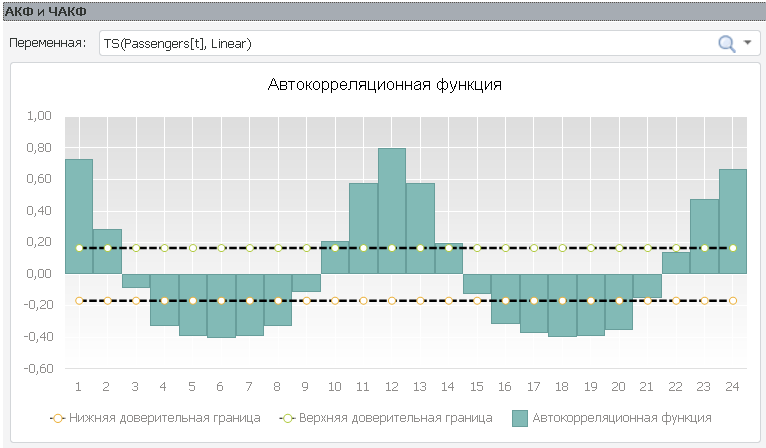
Если на графике АКФ видны периодические всплески, значит, в ряду присутствует сезонность. Пример расположен ниже.
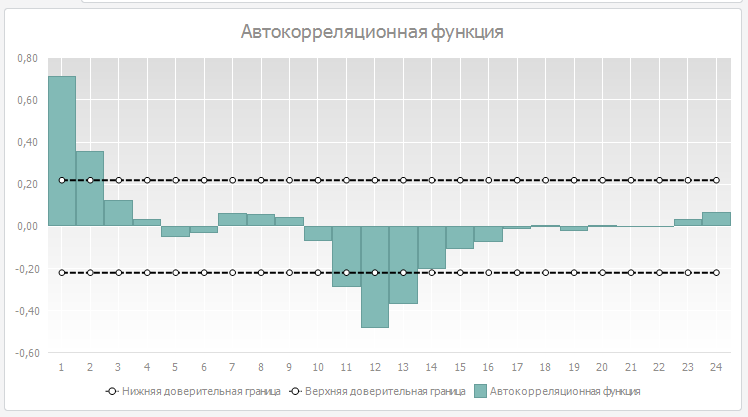
Анализируя рисунок АКФ исследуемого ряда (расположен ниже) можно сказать, что тренд в ряду отсутствует. Зато присутствует сезонность 12 порядка.
ЧАКФ отличается от АКФ тем, что не учитывает влияние промежуточных лагов при расчете частных коэффициентов корреляций. Поэтому ЧАКФ дает более «чистую картину» зависимости ряда от лага.
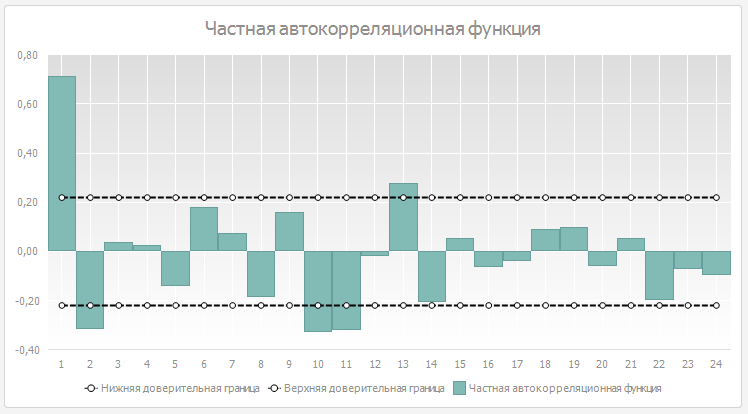
На лаге 1 обе функции будут иметь одинаковые значение. ЧАКФ позволяет определить порядок авторегрессора, который окажется значимым в модели.
Так, для исследуемого ряда будет значим лаг 1-го, 2-го, 10-го, 11-го, 12-го порядка.
Другими словами, можно сказать, что инфляция зависит от самой себя 1 период, 2 периода и т.д. назад.
Обе функции зависят от длины ряда. Чем больше длина ряда, тем более четко выраженными они окажутся.
Таким образом, для нашего ряда можно выделить 1, 2, 10, 11, 12 лаги. Также можно сказать, что отсутствует тренд и присутствует сезонность.
Для исследования наличия процессов скользящего среднего анализ АКФ и ЧАКФ происходит в обратном порядке. Сначала исследуется функция ЧАКФ на убывание, а затем АКФ на уровень порядка скользящего среднего.
Для нашего ряда можно будет исследовать скользящее среднее 1-го порядка.
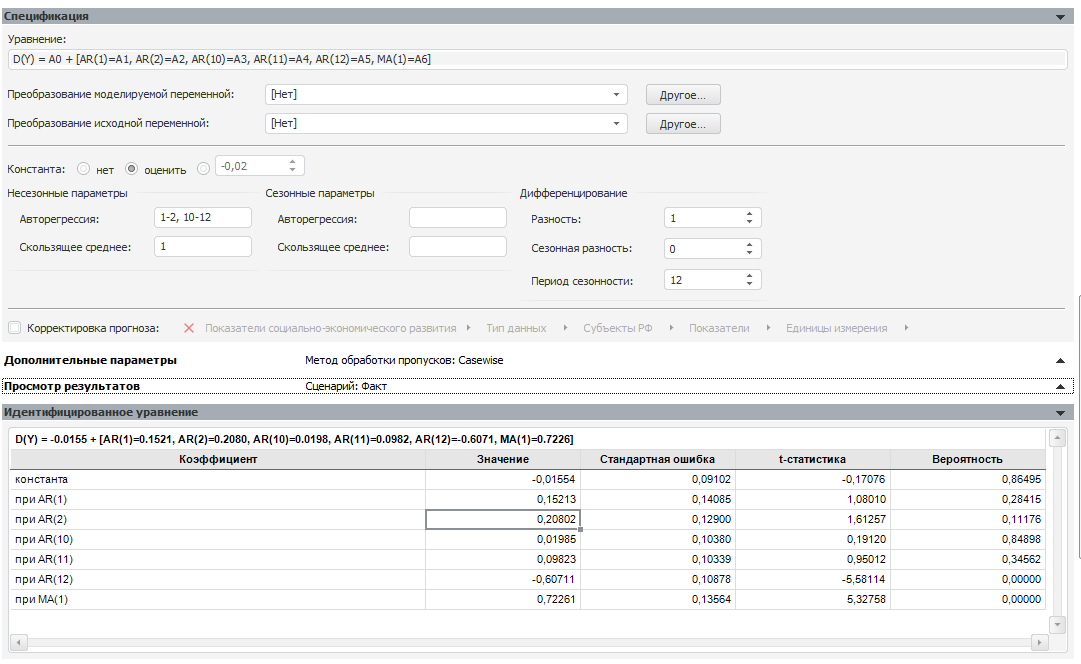
Таким образом, для исследуемого ряда необходимо построить модели с приведенными ниже параметрами.
Анализ факторов
Проведем анализ значимости каждого фактора. Значимость фактора смотрится по столбцу «Вероятность». Если фактор значим, то значение в этом столбце не должно превышать 0,05.
Теперь будем по очереди исключать самые незначимые факторы. Первым фактором, который исключим будет AR (10). Обратите внимание, что константа в данном анализе не участвует.
Теперь мы добились того, чтобы все факторы оказались значимыми.
Таким образом, мы говорим, что инфляция зависит сама от себя 2 периода и 12 периодов назад, а также от скользящего среднего ошибок модели.
Критерии качества
Теперь можно обратить внимание на критерии качества модели и график прогноза.
Анализ адекватности модели можно разделить на два этапа:
1. Этап оценки критериев качества модели.
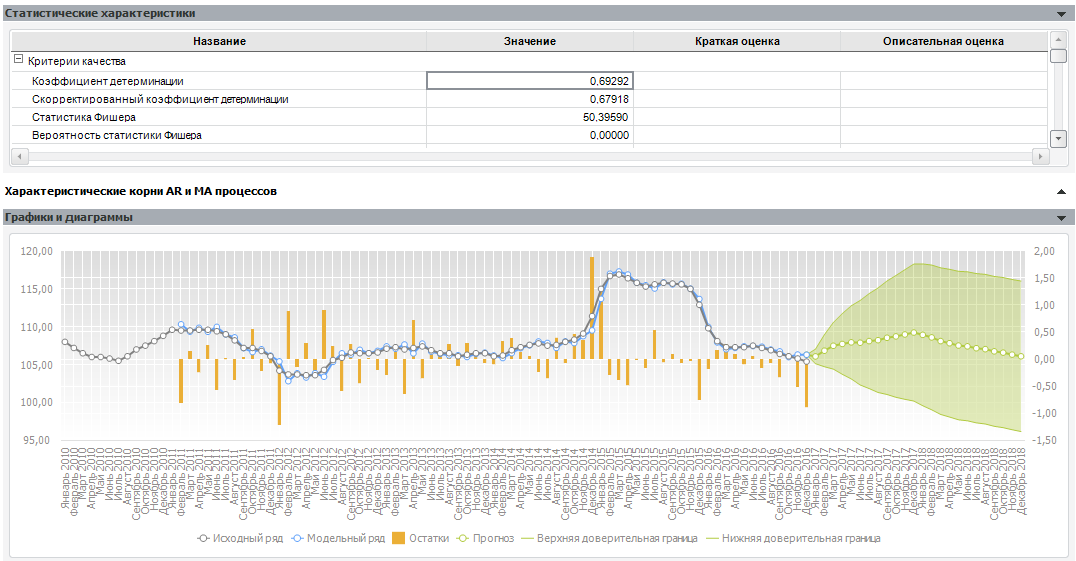
Коэффициент детерминации модели может принимать значение от 0 до 1. Чем ближе к 1, тем лучше качество модели. Данный коэффициент говорит о проценте изменчивости ряда, которая уловила модель. Так, наша модель описала 69% изменчивости ряда, что говорит о приемлемом результате.
Вероятность статистки Фишера говорит о вероятности ошибочного значения коэффициента детерминации. Для того чтобы принять результат, она должна составлять не более 0,05.
2. Анализ адекватности прогноза.
Далее необходимо посмотреть, соответствует ли прогноз ряду или нет. В нашем случае критичных ошибок, таких как экспоненциальный рост или странная динамика ряда, не наблюдается.
Если прогноз или критерии качества не удовлетворяют требованиям, то необходимо скорректировать модель, добавив другие лаги либо ещё одно скользящее среднее.
Прогноз, полученный после первой итерации достаточно адекватен, так что остановимся на ней.
А что в итоге?
В результате, на выходе модели мы получили прогноз по исследуемому ряду. Видно, что прогноз инфляции растет к концу 2017 года и снижается к концу 2018-го. Данный результат в дальнейшем может использоваться при принятии каких-либо управленческих решений. Например, зная, что будет рост инфляции к концу года, можно закупить сейчас долгохранящийся товар (малый бизнес) или оформить форвард по текущей цене (крупный бизнес).
Так, например, если бы мы взяли вместо инфляции ряд продаж по товару, то на основе прогноза продаж мы могли посчитать возможную прибыль от этого товара, рентабельность, а также с учетом данных склада сформировать заказ на закупку товара.
Параметры R-ARIMA. Как определить параметры аримы (p,d,q)?
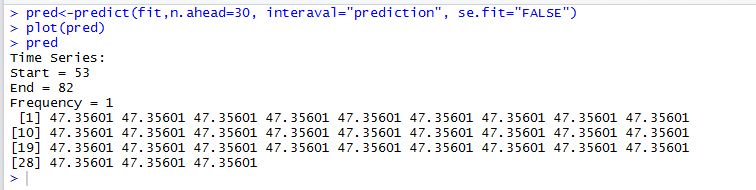
У меня есть еженедельные значения данных, извлеченные из трендов Google, и я хочу применить временной ряд в R для прогнозирования будущих значений. Я пытался использовать auto.arima(), но результаты кажутся только одним постоянным значением для всего будущего прогноза, и если я вручную даю случайные параметры в ариме (c(p,d,q)), я получаю различные типы Результаты. Итак, как определить соответствующие значения для моих данных.
3 ответа
В этом ответе предполагается, что вы знаете, что означают параметры (p,d и q), если нет, вам нужно немного почитать. Теперь в вызове ARIMA нужно указать два набора параметров: трендовый и сезонный.
Когда у вас есть представление о том, есть ли необходимость в трендовых и / или сезонных разностях, вы можете попробовать некоторые значения для параметра d и / или D и визуализировать разностный ряд, чтобы выбрать подходящее значение. Или вы можете выполнить ACF для разностного ряда и остановиться до того, как корреляция закончится, начиная с отрицательного значения.
Теперь сделайте ACF и PACF на разностных (стационарных) сериях. Определите, какие лаги вы хотите сохранить для условий AR/MA. Обычно поддержание ненулевого значения одного из них должно быть нормальным. Как правило, если ACF быстро падает до отрицательных значений, используйте MA, в противном случае, если он падает постепенно, используйте AR.
Построение модели SARIMA с помощью Python+R
Введение
Установка и настройки Rpy2
Для начала работы надо установть rpy2. Сделать это можно с помощью команды:
Начало работы
Итак, если вы работаете в IPython Notebook, нужно добавить инструкцию:
Данное расширение позволяет вызывать некторые функции R через rpy2, и выводит результат прямо в консоль IPython Notebook, что очень удобно (ниже будет показано как это сделать). Подробнее написано здесь.
Теперь же загрузим, нужные библиотеки:
Теперь, как и в предыдущей статье, загрузим данные и перейдем к недельным интервалам:

Итак, из графика можно заметить ежегодную сезонность (52 недели) и ярко выраженный тренд. Поэтому перед построением модели нам необходимо избавиться от тренда и сезонности.
Предварительный анализ данных
Итак для начала, прологорифмируем исходный ряд, для выравнивания значений:

Как видно у нас в графике присутствует сезонность и соответственно ряд не стационарен. Проверим это с помощью теста Дикки-Фулера, который проверяет гипотизу о наличии единичных корней и соотвтвенно если они есть ряд будет не стационарным. Как провести данный тест с помощью библиотеки statsmodels, я показывал в прошлый раз. Сейчас я продемонстрирую как это можно сделать с помощью функции adf.test() из R.
Итак, данная функция находится в R-ой библиотеке tseries. Она предназначена для анализа временных рядов и устанавливается дополнительно. Загрузить нужную библиотеку можно с помощью функции importr().
Можно заметить, что кроме tseries, мы загрузили еще и библиотеку stats. Она нам понадобитьсядля преобразования типов.
Теперь необходимо перевести данные из типа Python в тип понятный R. Сделать это можно с помощью функции convert_to_r_dataframe() на вход которой подается DataFrame, а на выходе получается вектор для R.
Итак, вектор есть следующим шагом надо перевести его в формат временного ряда. Для этого в R существует функция ts(), вызов ее будет выглядеть так:
Предварительная подготовка данных закончена и мы можем вызвать нужную нам функцию:
В качестве параметров ей передается временный ряд и количество лагов, для которых будет расчитываться тест. В экономических моделях принято брать данное значение равное году, а т.к. данные у нас еженедельные, а в году 52 недели, поэтому параметр имеет такое значение.
Теперь в переменной ad содержится R-объект. Его структура описана в виде списка, описание которого мне найти не удалось. Поэтому с помощью визуального анализа я написал код, который выводит результат работы функции в понятном виде:
Исходя из результатов теста, исходный ряд не стационарен. Т.к. гипотеза о наличии единичных корней принимается с малой вероятностью, и, соответственно, ряд не стационарен. Теперь проверим на стационарность ряд первых разностей.
Для начала получим их с помощью Python, а затем применим ADF-тест:

Ряд первых разностей, по итогам теста, оказался стационарным. А график помогает нам убедиться, что тенденция отсутствует. Осталось избавиться от сезонности.
Для этого нужно взять сезонную разность, от нашего получившегося ряда. Подробнее можно прочитать тут. Если полученный ряд будет стационармы необходимо будет вязть его превую разность и проверить ее.
Проверим ее на стационарность с помощью ADF-тест из R:
Итак, ряд не стационарен, возьмем его первые разности:
Получившийся ряд стационарен. Теперь можно перейти к построению модели
Построение модели.
Как определять p, d, q, я показывал в прошлый раз. Сейчас я опишу определять порядок сезонных составляющих P,D,Q.
Начнем с определения параметра D. Он определет порядок интегрированности сезонной разности, т.е. в нашем случае он равен 1. Для определения P и Q нам как и прежде надо построить коррелограммы ACF и PACF.
Порядок модели передается в качестве вектора R, поэтому давайте создадим его:
Так же в качестве параметра сезонной составляющей передается список, который содержит ее порядок и размер периода:
Теперь мы готовы к тому, чтобы построить модель:
Итак наша модель готова и можно перейти к построению прогноза на ее основе.
Проверка адекватности модели.
Итак для проверки адекватности модели надо проверить соответвуют ли остатки модели «белому шуму». Проверим это проведя Q-тест Льюнга — Бокса и проверим корреляцию остатков. Для этого в R существует функция tsdiag(), в качестве параметра передается модель и количество лагов для теста.
Вызвать данную функцию можно так:

В первой строке инструкция %Rpush загружает объекты для использования в R. Иструкция %R во второй строке вызывает код в формате языка R. Данная конструкция работает в IPython Notebook.
Из графиков выше можно заметить, что остатки независимы (это видно по ACF). Кроме того из графика Q-статистики можно заметить что во всех точках значение p-value больше уровня значимости, из этого можно сделать вывод, что остатки, с большой вероятностью, являются «белым шумом».
Прогнозирование
Для прогонизования нужно подгрузить библиотеку forecast
Вывести результы прогнозирования можно двумя способами.
Способ 1. Это использовать возможности интеграции IPython и R. Который был показан в предыдущем разделе:
Способ 2. Второй способ это сделать прогноз с помощью библиотеки forecast, а потом перевести результат в во временную серию pandas и вывести их на экран. Код который будет выполнять написан ниже:
Как создать модель ARIMA для прогнозирования временных рядов в Python
Дата публикации 2017-01-09
Популярным и широко используемым статистическим методом для прогнозирования временных рядов является модель ARIMA.
В этом руководстве вы узнаете, как разработать модель ARIMA для данных временных рядов с помощью Python.
После завершения этого урока вы узнаете:
Модель авторегрессии с интегрированным скользящим средним
Модель ARIMAкласс статистических моделей для анализа и прогнозирования данных временных рядов.
Он явно обслуживает набор стандартных структур данных временных рядов и, как таковой, предоставляет простой, но мощный метод для создания искусных прогнозов временных рядов.
Эта аббревиатура носит описательный характер и отражает ключевые аспекты самой модели. Вкратце, это:
Каждый из этих компонентов явно указан в модели в качестве параметра. Используется стандартное обозначение ARIMA (p, d, q), где параметры заменяются целочисленными значениями для быстрого указания конкретной используемой модели ARIMA.
Параметры модели ARIMA определяются следующим образом:
Построена модель линейной регрессии, включающая определенное количество и тип терминов, и данные подготавливаются по степени разности, чтобы сделать ее стационарной, то есть удалить трендовые и сезонные структуры, которые негативно влияют на модель регрессии.
Значение 0 может быть использовано для параметра, который указывает, что этот элемент модели не используется. Таким образом, модель ARIMA может быть сконфигурирована для выполнения функции модели ARMA и даже простой модели AR, I или MA.
Принятие модели ARIMA для временного ряда предполагает, что базовый процесс, который произвел наблюдения, является процессом ARIMA. Это может показаться очевидным, но помогает мотивировать необходимость подтверждения допущений модели в необработанных наблюдениях и в остаточных ошибках прогнозов из модели.
Далее, давайте посмотрим, как мы можем использовать модель ARIMA в Python. Начнем с загрузки простого одномерного временного ряда.
Набор данных по продажам шампуня
Этот набор данных описывает ежемесячное количество продаж шампуня за 3-летний период.
Единицами являются количество продаж и 36 наблюдений. Оригинальный набор данных приписан Макридакису, Уилрайту и Хиндману (1998).
Загрузите набор данных и поместите его в текущий рабочий каталог с именем файла «Шампунь-sales.csv«.
Ниже приведен пример загрузки набора данных Shampoo Sales с помощью Pandas с пользовательской функцией для анализа поля даты и времени. Набор данных базируется в произвольном году, в данном случае 1900.
При выполнении примера печатаются первые 5 строк набора данных.
Данные также представлены в виде временного ряда с месяцем по оси X и показателями продаж по оси Y.
Мы видим, что набор данных по продажам шампуней имеет четкую тенденцию.
Это говорит о том, что временной ряд не является стационарным и потребует разности, чтобы сделать его стационарным, по крайней мере, с разницей порядка 1.
Давайте также кратко рассмотрим график автокорреляции временных рядов. Это также встроено в Панд. В приведенном ниже примере показана автокорреляция для большого числа лагов во временном ряду.
Приведя пример, мы можем видеть, что существует положительная корреляция с первыми 10–12 лагами, которая, возможно, значима для первых 5 лагов.
Хорошей отправной точкой для параметра AR модели может быть 5.
Арима с питоном
Библиотека statsmodels предоставляет возможность соответствовать модели ARIMA
Модель ARIMA может быть создана с использованием библиотеки statsmodels следующим образом:
Давайте начнем с чего-то простого. Мы подгоним модель ARIMA ко всему набору данных Shampoo Sales и рассмотрим остаточные ошибки.
Сначала мы подходим к модели ARIMA (5,1,0). Это устанавливает значение задержки равным 5 для авторегрессии, использует порядок разности 1, чтобы сделать временной ряд стационарным, и использует модель скользящего среднего 0.
При подгонке модели предоставляется много отладочной информации о подгонке модели линейной регрессии. Мы можем отключить это, установивИндик.точкиаргумент 0.
При запуске примера выводится сводная информация о подходящей модели. Это суммирует используемые значения коэффициента, а также умение подгонки по наблюдениям в выборке.
Во-первых, мы получаем линейный график остаточных ошибок, предполагая, что все еще может быть некоторая информация о тренде, не уловленная моделью.
Затем мы получаем график плотности значений остаточных ошибок, предполагая, что ошибки являются гауссовыми, но могут не центрироваться на нуле.
Распределение остаточных ошибок отображается. Результаты показывают, что в прогнозе действительно есть смещение (ненулевое среднее в невязках).
Обратите внимание, что, хотя выше мы использовали весь набор данных для анализа временных рядов, в идеале мы должны выполнять этот анализ только для обучающего набора данных при разработке прогностической модели.
Далее, давайте посмотрим, как мы можем использовать модель ARIMA для составления прогнозов.
Скользящий прогноз Модель ARIMA
Модель ARIMA может использоваться для прогнозирования будущих временных шагов.
Мы можем использовать функцию предиката () наARIMAResultsобъект, чтобы делать прогнозы. Он принимает индекс временных шагов, чтобы делать прогнозы в качестве аргументов. Эти индексы относятся к началу набора обучающих данных, используемого для прогнозирования.
Если бы мы использовали 100 наблюдений в обучающем наборе данных, чтобы соответствовать модели, тогда индекс следующего временного шага для прогнозирования был бы указан для функции прогнозирования какначало = 101, конец = 101, Это вернет массив с одним элементом, содержащим прогноз.
Мы также предпочли бы, чтобы прогнозируемые значения находились в исходной шкале, если мы выполнили какое-либо различие (д & при 0при настройке модели). Это можно указать, установивтиповоеаргумент к значению«уровни»:станд =»уровни,
Кроме того, мы можем избежать всех этих спецификаций, используяпрогноз()функция, которая выполняет одношаговый прогноз с использованием модели.
Мы можем разделить набор обучающих данных на наборы поездов и тестов, использовать набор поездов для соответствия модели и сгенерировать прогноз для каждого элемента в тестовом наборе.
Скользящий прогноз требуется с учетом зависимости от наблюдений в предыдущих временных шагах для разности и модели AR. Грубый способ выполнить этот скользящий прогноз состоит в том, чтобы заново создать модель ARIMA после получения каждого нового наблюдения.
Мы вручную отслеживаем все наблюдения в списке, называемом историей, который заполняется данными обучения и к которому добавляются новые наблюдения на каждой итерации.
Сложив все это вместе, ниже приведен пример скользящего прогноза с моделью ARIMA в Python.
Выполнение примера выводит прогноз и ожидаемое значение для каждой итерации.
Мы также можем рассчитать окончательный среднеквадратичный показатель ошибки (MSE) для прогнозов, предоставляя точку сравнения для других конфигураций ARIMA.
Создается линейный график, показывающий ожидаемые значения (синим цветом) по сравнению с прогнозами скользящего прогноза (красным). Мы можем видеть, что значения показывают некоторую тенденцию и находятся в правильном масштабе.
Модель может использовать дальнейшую настройку параметров p, d и, возможно, даже q.
Конфигурирование модели ARIMA
Это процесс, который использует анализ и диагностику временных рядов для определения хороших параметров модели ARIMA.
Таким образом, шаги этого процесса заключаются в следующем:
Процесс повторяется до тех пор, пока не будет достигнут желаемый уровень соответствия для наблюдений в выборке или вне выборки (например, наборы обучающих или тестовых данных)
Процесс описан в классическом учебнике 1970 года по темеАнализ временных рядов: прогнозирование и контрольДжордж Бокс и Гвилим Дженкинс. Обновленное 5-е издание теперь доступно, если вы хотите углубиться в этот тип модели и методологии.
Принимая во внимание, что модель может эффективно вписываться в наборы данных временных рядов небольшого размера, параметры поиска по сетке модели могут быть ценным подходом.
Резюме
В этом руководстве вы узнали, как разработать модель ARIMA для прогнозирования временных рядов в Python.
В частности, вы узнали:
У вас есть вопросы об ARIMA или об этом уроке?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.