поиск самоподобных областей в изображении и определение для них параметров аффинных преобразований

АЛГОРИТМЫ СЖАТИЯ

Фрактальный алгоритм

История фрактального сжатия

Рождение фрактальной геометрии обычно связывают с выходом в 1977 году книги Б. Мандельброта «Фрактальная геометрия природы». Одна из основных идей книги заключалась в том, что средствами традиционной геометрии (то есть используя линии и поверхности), чрезвычайно сложно представить природные объекты. Фрактальная геометрия задает их очень просто.

В 1981 году Джон Хатчинсон опубликовал статью «Фракталы и самоподобие», в которой была представлена теория построения фракталов с помощью системы итерируемых функций (IFS, Iterated Function System). Четыре года спустя появилась статья Майкла Барнсли и Стефана Демко, в которой приводилась уже достаточно стройная теория IFS. В 1987 году Барнсли основал Iterated Systems, компанию, основной деятельностью которой является создание новых алгоритмов и ПО с использованием фракталов. Всего через год, в 1988 году, он выпустил фундаментальный труд «Фракталы повсюду». Помимо описания IFS, в ней был получен результат, известный сейчас как Collage Theorem, который лежит в основе математического обоснования идеи фрактальной компрессии.

Если построение изображений с помощью фрактальной математики можно назвать прямой задачей, то построение по изображению IFS – это обратная задача. Довольно долго она считалась неразрешимой, однако Барнсли, используя Collage Theorem, построил соответствующий алгоритм. (В 1990 и 1991 годах эта идея была защищена патентами.) Если коэффициенты занимают меньше места, чем исходное изображение, то алгоритм является алгоритмом архивации.

Первая статья об успехах Барнсли в области компрессии появилась в журнале BYTE в январе 1988 года. В ней не описывалось решение обратной задачи, но приводилось несколько изображений, сжатых с коэффициентом 1:10000, что было совершенно ошеломительно. Но практически сразу было отмечено, что несмотря на броские названия («Темный лес», «Побережье Монтере», «Поле подсолнухов») изображения в действительности имели искусственную природу. Это, вызвало массу скептических замечаний, подогреваемых еще и заявлением Барнсли о том, что «среднее изображение требует для сжатия порядка 100 часов работы на мощной двухпроцессорной рабочей станции, причем с участием человека».

В 1994 году Ювал Фишер были предоставил во всеобщее пользование исходные тексты исследовательской программы, в которой использовалось разложение изображения в квадродерево и были реализованы алгоритмы оптимизации поиска. Позднее появилось еще несколько исследовательских проектов, которые в качестве начального варианта программы использовали программу Фишера. В июле 1995 года в Тронхейме (Швеция) состоялась первая школа-конференция, посвященная фрактальной компрессии.

Идея метода

Фрактальная архивация основана на том, что мы представляем изображение в более компактной форме – с помощью коэффициентов системы итерируемых функций (Iterated Function System – далее по тексту как IFS). Строго говоря, IFS представляет собой набор трехмерных аффинных преобразований, в нашем случае переводящих одно изображение в другое. Преобразованию подвергаются точки в трехмерном пространстве (х_координата, у_координата, яркость).

Расставляя линзы и меняя их характеристики, мы можем управлять получаемым изображением. Одна итерация работы машины заключается в том, что по исходному изображению с помощью проектирования строится новое, после чего новое берется в качестве исходного. Утверждается, что в процессе итераций мы получим изображение, которое перестанет изменяться. Оно будет зависеть только от расположения и характеристик линз, и не будет зависеть от исходной картинки. Это изображение называется «неподвижной точкой» или аттрактором данной IFS. Соответствующая теория гарантирует наличие ровно одной неподвижной точки для каждой IFS.

Поскольку отображение линз является сжимающим, каждая линза в явном виде задает самоподобные области в нашем изображении. Благодаря самоподобию мы получаем сложную структуру изображения при любом увеличении. Таким образом, интуитивно понятно, что система итерируемых функций задает фрактал (нестрого – самоподобный математический объект).

Наиболее известны два изображения, полученных с помощью IFS: «треугольник Серпинского» и «папоротник Барнсли».

Папоротник Барнсли. Задается 4 преобразованиями.

Треугольник Серпинского. Задается 3 преобразованиями.

«Треугольник Серпинского» задается тремя, а «папоротник Барнсли» четырьмя аффинными преобразованиями (или, в нашей терминологии, «линзами»). Каждое преобразование кодируется считанными байтами, в то время как изображение, построенное с их помощью, может занимать и несколько мегабайт.

Из вышесказанного становится понятно, как работает архиватор, и почему ему требуется так много времени. Фактически, фрактальная компрессия – это поиск самоподобных областей в изображении и определение для них параметров аффинных преобразований.

В худшем случае, если не будет применяться оптимизирующий алгоритм, потребуется перебор и сравнение всех возможных фрагментов изображения разного размера. Даже для небольших изображений при учете дискретности мы получим астрономическое число перебираемых вариантов. Причем, даже резкое сужение классов преобразований, например, за счет масштабирования только в определенное количество раз, не дает заметного выигрыша во времени. Кроме того, при этом теряется качество изображения. Подавляющее большинство исследований в области фрактальной компрессии сейчас направлены на уменьшение времени архивации, необходимого для получения качественного изображения.

Математические основы фрактального сжатия

Далее приводятся основные определения и теоремы, на которых базируется фрактальная компрессия.

где a, b, c, d, e, f действительные числа и (x y) принадлежит R 2 называется двумерным аффинным преобразованием.

где a, b, c, d, e, f, p, q, r, s, t, u действительные числа и (x y z) принадлежит R 3 называется трехмерным аффинным преобразованием.

Определение. Пусть f:X –> X – преобразование в пространстве Х. Точка x_f принадлежащая X такая, что f(x_f)=x_f называется неподвижной точкой (аттрактором) преобразования.

Определение. Пусть f:X–>X в метрическом пространстве (Х, d) называется сжимающим, если существует число s: 0 X в полном метрическом пространстве (Х, d). Тогда существует в точности одна неподвижная точка x_f принадлежащая X этого преобразования, и для любой точки x принадлежащей X последовательность сходится к x_f.

Более общая формулировка этой теоремы гарантирует нам сходимость.

Определение. Изображением называется функция S, определенная на единичном квадрате и принимающая значения от 0 до 1 или S(x,y) принадлежит [0. 1] для любых x,y принадлежащих [0. 1].

и определено на компактном подмножестве D_i декартова квадрата [0..1]x[0..1]. Тогда оно переведет часть поверхности S в область R_i, расположенную со сдвигом (e,f) и поворотом, заданным матрицей

При этом, если интерпретировать значение S как яркость соответствующих точек, она уменьшится в p раз (преобразование обязано быть сжимающим) и изменится на сдвиг q.

Определение. Конечная совокупность W сжимающих трехмерных аффинных преобразований w_i, определенных на областях D_i, таких, что w_i(D_i) = R_i и пересечение R_i с R_j является пустым множеством, называется системой итерируемых функций (IFS).

Системе итерируемых функций однозначно сопоставляется неподвижная точка – изображение. Таким образом, процесс компрессии заключается в поиске коэффициентов системы, а процесс декомпрессии – в проведении итераций системы до стабилизации полученного изображения (неподвижной точки IFS). На практике бывает достаточно 7-16 итераций. Области R_i в именуются ранговыми, а области D_i – доменными.

Типовая схема фрактального сжатия

Первые три условия означают, что отображение w_i будет сжимающим. А в силу четвёртого условия кодируемое изображение R и его образ W(R) будут похожи друг на друга. В идеале R = W(R). А это означает, что изображение R и будет являться неподвижной точкой W. Именно здесь используется подобие различных частей изображения. Как оказалось, практически все реальные изображения содержат такие похожие друг на друга, с точностью до аффинного преобразования, части.

Сравнение с JPEG

Сегодня наиболее распространенным алгоритмом архивации графики является JPEG. Сравним его с фрактальной компрессией.

Во-первых, заметим, что и тот, и другой алгоритм оперируют 8-битными (в градациях серого) и 24-битными полноцветными изображениями. Оба являются алгоритмами сжатия с потерями и обеспечивают близкие коэффициенты архивации. И у фрактального алгоритма, и у JPEG существует возможность увеличить степень сжатия за счет увеличения потерь. Кроме того, оба алгоритма очень хорошо распараллеливаются.

Различия начинаются, если мы рассмотрим время, необходимое алгоритмам для архивации/разархивации. Так, фрактальный алгоритм сжимает в сотни и даже в тысячи раз дольше, чем JPEG. Распаковка изображения, наоборот, произойдет в 5-10 раз быстрее. Поэтому, если изображение будет сжато только один раз, а передано по сети и распаковано множество раз, то выгодней использовать фрактальный алгоритм.

JPEG использует разложение изображения по косинусоидальным функциям, поэтому потери в нем (даже при заданных минимальных потерях) проявляются в волнах и ореолах на границе резких переходов цветов. Именно за этот эффект его не любят использовать при сжатии изображений, которые готовят для качественной печати: там этот эффект может стать очень заметен. Фрактальный алгоритм избавлен от этого недостатка. Более того, при печати изображения каждый раз приходится выполнять операцию масштабирования, поскольку растр печатающего устройства не совпадает с растром изображения. При преобразовании также может возникнуть несколько неприятных эффектов, с которыми можно бороться либо масштабируя изображение программно, либо снабжая устройство печати своим процессором, винчестером и набором программ обработки изображений. Как можно догадаться, при использовании фрактального алгоритма таких проблем практически не возникает.

Вытеснение JPEG фрактальным алгоритмом в повсеместном использовании произойдет еще не скоро (хотя бы в силу низкой скорости архивации последнего), однако в области приложений мультимедиа, в компьютерных играх его использование вполне оправдано.

Характеристики фрактального алгоритма

Коэффициенты компрессии: 2-2000 (Задается пользователем).

Класс изображений: Полноцветные 24 битные изображения или изображения в градациях серого без резких переходов цветов (фотографии). Желательно, чтобы области большей значимости (для восприятия) были более контрастными и резкими, а области меньшей значимости — неконтрастными и размытыми.

Характерные особенности: Может свободно масштабировать изображение при разархивации, увеличивая его в 2-4 раза без появления «лестничного эффекта». При увеличении степени компрессии появляется «блочный» эффект на границах блоков в изображении.

Источник

Основы фрактального сжатия изображений

Несколько аффинных сжимающих отображений образуют систему итерированных функций (СИФ). По сути, СИФ — это множительная машина. Она принимает исходное изображение, искажает его, перемещает, и так несколько раз.
Например, вот так при помощи СИФ из трех функций строится треугольник Серпинского:

Исходный треугольник три раза множится, уменьшается и переносится. И так далее. Если так продолжать до бесконечности, получим известный фрактал площадью 0 и размерностью 1,585.

Если функции, входящие в СИФ,— сжимающие, то сама СИФ тоже имеет неподвижную точку. Вот только эта «точка» будет уже не привычной нам точкой в N-мерном пространстве, а множеством таких точек, то есть изображением. Оно называется аттрактором СИФ. Для СИФ, приведенной выше, аттрактором будет треугольник Серпинского.

Имея СИФ, найти аттрактор просто. Во всяком случае, имея под рукой компьютер. Можно взять абсолютно любое начальное изображение и начать применять к нему СИФ. Пример с тем же треугольником, но уже построенным из квадрата:

Получается, что для построения довольно сложной фигуры нам потребовалось 18 коэффициентов. Выигрыш, как говорится, налицо.
Вот если бы мы умели решать обратную задачу — имея аттрактор, строить СИФ… Тогда достаточно взять аттрактор-изображение, похожее на фотографию вашей кошки и можно довольно выгодно его закодировать.

Вот здесь, собственно, начинаются проблемы. Произвольные изображения, в отличие от фракталов, не самоподобны, так что так просто эта задача не решается. Как это сделать придумал в 1992 году Арнольд Жакин, в то время — аспирант Майкла Барнсли, который считается отцом фрактального сжатия.

Самоподобие нам нужно обязательно — иначе ограниченные в своих возможностях аффинные преобразования не смогут правдоподобно приблизить изображения. А если его нет между частью и целым, то можно поискать между частью и частью. Примерно так, видимо, рассуждал и Жакин.

На картинке ранговый блок обозначен жёлтым, соответствующий ему доменный — красным. Также показаны этапы преобразования и результат.

Можете поиграться сами: Coder demo.

Получение оптимального преобразования — отдельная тема, однако большого труда оно не составляет. Но другой недостаток схемы виден невооруженным глазом. Можете сами подсчитать, сколько доменных блоков размером 32×32 содержит двухмегапиксельное изображение. Полный их перебор для каждого рангового блока и есть основная проблема такого вида сжатия — кодирование занимает очень много времени. Разумеется, с этим борются при помощи различных ухищрений, вроде сужения области поиска или предварительной классификации доменных блоков. С различным ущербом для качества.

Декодирование же производится просто и довольно быстро. Берем любое изображение, делим на ранговые области, последовательно заменяем их результатом применения соотв. преобразования к соотв. доменной области (что бы она ни содержала в данный момент). После нескольких итераций исходное изображение станет похоже на себя:

Пожалуй, для введения информации достаточно. Интересующиеся могут почитать соответствующие статьи в Википедии или соответствующем сообществе.

Подробное изложение можно найти в этой статье, с которой все началось в 1992 году. Большинство материалов, разумеется, на английском.

Источник

Компью А рт

Андрей Лёушкин фрилансер, г.Кокшетау (Казахстан)

После открытия Бенуа Мандельбротом теории фракталов стало понятно, что данная теория способна удивительно точно описывать многие объекты и явления окружающего нас мира. Неудивительно, что теория фракталов и фрактальные алгоритмы, в частности, нашли практическое применение в очень многих областях науки и техники. Собственно о практическом применении фрактальных алгоритмов и пойдет речь в данной статье. Фрактал-арт мы затрагивать не будем, о нем достаточно подробно написано в предыдущей статье.

Фрактальное сжатие изображений

Первым и очевидным применением фрактальных алгоритмов стало так называемое фрактальное сжатие изображений. Фрактальное сжатие изображений — это алгоритм сжатия изображений с потерями, основанный на применении систем итерируемых функций к изображениям. Системы итерируемых функций (СИФ) представляют собой системы функций из некоторого фиксированного класса функций, отображающих одно многомерное множество на другое. Данный алгоритм известен тем, что в некоторых случаях позволяет получать очень высокие коэффициенты сжатия. Лучшие примеры — до 1000 раз (при приемлемом визуальном качестве) — для реальных фотографий природных объектов, что недоступно для других алгоритмов сжатия изображений в принципе.1

Основа метода фрактального кодирования — это обнаружение самоподобных участков в изображении. Впервые возможность применения теории систем итерируемых функций к проблеме сжатия изображения была исследована Майклом Барнсли (Michael Barnsley) и Аланом Слоуном (Alan Sloan). Они запатентовали свою идею в 1990 и 1991 годах.

Фрактальная архивация основана на том, что с помощью коэффициентов системы итерируемых функций изображение представляется в более компактной форме. Наиболее наглядно этот процесс представил сам Барнсли в своей книге «Фрактальное сжатие изображения». В ней введено понятие фотокопировальной машины. Такая машина состоит из экрана, на котором изображена исходная картинка, и системы линз, проецирующих изображение на другой экран. Каждая линза проецирует часть исходного изображения. Расставляя линзы и меняя их характеристики, можно управлять получаемым изображением. На линзы налагается требование: они должны уменьшать в размерах проецируемую часть изображения. Кроме того, они могут менять яркость фрагмента и проецируют не круги, а области с произвольной границей.

Один шаг машины состоит в построении — с помощью проецирования по исходному — нового изображения. Утверждается, что на некотором шаге изображение перестанет изменяться. Оно будет зависеть только от расположения и характеристик линз и не будет зависеть от исходной картинки. Это изображение называется неподвижной точкой или аттрактором данной СИФ. Теорема Collage Theorem гарантирует наличие ровно одной неподвижной точки для каждой СИФ. Поскольку отображение линз является сжимающим, каждая линза в явном виде задает самоподобные области в нашем изображении. Благодаря самоподобию мы получаем сложную структуру изображения при любом увеличении.

Наиболее известны два изображения, полученных с помощью СИФ: треугольник Серпинского и папоротник Барнсли (рис. 1). Первое задается тремя, а второе — пятью аффинными преобразованиями (или, в нашей терминологии, линзами). Каждое преобразование задается буквально считаными байтами, в то время как изображение, построенное с их помощью, может занимать и несколько мегабайт.

Рис. 1. Треугольник Серпинского и папоротник Барнсли

Становится понятно, как работает архиватор и почему ему требуется так много времени. Фактически, фрактальная компрессия — это поиск самоподобных областей в изображении и определение для них параметров аффинных преобразований.

В худшем случае, если не будет применяться оптимизирующий алгоритм, потребуется перебор и сравнение всех возможных фрагментов изображения разного размера. Даже для небольших изображений при учете дискретности мы получим астрономическое число перебираемых вариантов. Даже резкое сужение классов преобразований, например за счет масштабирования только в определенное число раз, не позволит добиться приемлемого времени. Кроме того, при этом теряется качество изображения. Подавляющее большинство исследований в области фрактальной компрессии сейчас направлено на уменьшение времени архивации, необходимого для получения качественного изображения.

Фракталы как элементы визуализации и спецэффектов

Фракталы притягивают и завораживают своей красотой и бесконечностью. Именно поэтому (и не только) фракталы очень часто используют для создания различного рода визуализаций, видеоинсталляций, создания спецэффектов в компьютерной графике и т.д.

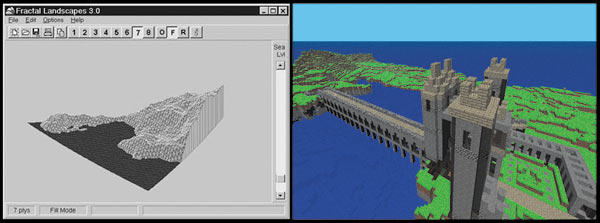
Начнем, пожалуй, с игр. Сегодня в очень многих играх (самый яркий пример — Minecraft, рис. 2), где присутствуют красивые природные ландшафты, так или иначе используются фрактальные алгоритмы. Этот способ зарекомендовал себя довольно эффективно. Дело в том, что настоящие природные объекты имеют в своей основе фрактальную структуру. Взяв это на вооружение, программисты предприняли попытку создать компьютерные ландшафты на базе фрактальных алгоритмов. Наблюдая сегодняшнее многообразие игр с красивыми природными ландшафтами, можно сказать — им это удалось. Более того, создано большое количество программ для генерации ландшафтов и пейзажей, основанных на фрактальных алгоритмах.

Не обошлось без фракталов и в кино, где для создания различных фантастических пейзажей (как и в играх) используется тот же принцип. Действительно, зачем каждый раз создавать новое дерево или гору, тратя кучу времени, когда всё это можно во много раз быстрее сделать с помощью компьютерных программ, работающих на фрактальных алгоритмах. Интересный факт: в известном космическом хорроре «Чужой» Ридли Скотта, в эпизоде, когда команда спускается на поверхность планеты, монитор в корабле передает изображение поверхности планеты в виде сетки. Именно это изображение было создано при помощи фрактальной геометрии. Фрактальная геометрия позволяет художникам по спецэффектам без труда создавать такие объекты, как облака, дым, пламя, звездное небо и т.д.

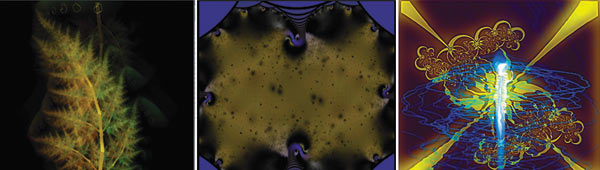
Теперь немного затронем тему фрактальной анимации. Фрактальные изображения, созданные в различных генераторах, необычайно красивы. Что уж тогда говорить о фрактальной анимации?! Это действительно потрясающее зрелище. В первую очередь здесь стоит упомянуть о ресурсе Electric sheep, использующем распределенные вычисления для создания фрактальной анимации, основанной на алгоритме fractal flame (разработан Скоттом Дрейвсом — Scott Draves). Проще говоря, на компьютер устанавливается программное обеспечение, которое использует машину для вычисления и рендера фрактальной анимации. Одновременно с этим ПО загружает и демонстрирует уже готовую фрактальную анимацию в виде так называемых живых обоев, которые сохраняются в определенной папке. В дальнейшем их можно использовать в своих целях, например в видеомонтаже (правда, длина роликов коротковата — 5 секунд). Однако, имея в своем распоряжении программу «Апофизис» и скрипт к ней Apophymator, можно без особого труда создавать свою сколь угодно длинную анимацию (уроков по этой теме в Сети множество), главное, чтобы машина была достаточно мощной (рис. 3).

Рис. 3. Примеры фрактальных анимаций

Рис. 4. Анимированное множество Жюлиа плагина milkdrop

Зрелищность фрактальной анимации с успехом применяют и виджеи в своих видеосетах. Особенно часто такие видеоинсталляции используются на концертах электронной музыки. Для этого применяются так называемые программы виджеинга (например, Resolume). Фрактальную анимацию в качестве визуализации используют разработчики программ, напрямую не относящихся к фракталогенераторам. К примеру, хорошо известный проигрыватель Winamp имеет в своем наборе большое количество визуализаций (плагин milkdrop), в которых явно прослеживаются элементы фракталов, например анимированное множество Жюлиа (рис. 4).

Применение фракталов в телекоммуникациях

В телекоммуникациях фракталы применяются для создания фрактальных антенн (рис. 5) — относительно нового класса электрически малых антенн, принципиально отличающихся своей геометрией от известных решений. Традиционная эволюция антенн базировалась на евклидовой геометрии, оперирующей объектами целочисленной размерности (линия, круг, эллипс, параболоид и т.п.). Фрактальные антенны с удивительно компактным дизайном обеспечивают превосходную широкополосную производительность в маленьком формфакторе. Достаточно компактные для установки или встраивания в различных местах фрактальные антенны используются в морских, воздушных транспортных средствах или в персональных устройствах.

Рис. 5. Антенна в виде ковра Серпинского

В сфере сетевых технологий было также проведено множество исследований, показывающих самоподобие трафика, передаваемого по разного рода сетям. Особенно это касается речевых, аудио­ и видеосервисов. В связи с этим сейчас проводится изучение возможности фрактального сжатия трафика, передаваемого по сетям, для более эффективной передачи информации.

Применение фракталов в медицине

В настоящее время фракталы уже находят и, вероятно, будут и в дальнейшем находить применение в медицине. Человеческий организм состоит из множества фракталоподобных структур: кровеносная система, мышцы, бронхи и т.д., поэтому ученые задумались о возможности применения фрактальных алгоритмов для диагностики и лечения каких­либо заболеваний. Оказалось, что такая возможность существует. Теория фракталов, например, может применяться для анализа электрокардиограмм. В последние годы в развитых странах, несмотря на очевидные успехи в разработке новых лабораторных и инструментальных методов диагностики и лечения сердечно­сосудистых заболеваний, рост последних неуклонно продолжается. Периоды биоритмов, в частности сердечного ритма, длительностью порядка часа, суток и более можно изучать традиционными методами гистограммного или спектрального анализа. Однако оценка хроноструктуры величины и ритмов фрактальной размерности, индексов Херста позволяет на более ранней стадии и с большей точностью и информативностью судить о нарушениях гомеостазиса и о развитии конкретных заболеваний.

Фракталы могут использоваться также (пока на стадии экспериментов) в обработке медицинских рентгеновских изображений. Рентгеновские снимки, обработанные с помощью фрактальных алгоритмов, дают более качественную картинку, а следовательно — и более качественную диагностику!

Еще одна область медицины, где активно могут применяться фракталы — это гастроэнтерология. Для диагностики заболеваний желудочно­кишечного тракта (ЖКТ) по сей день используются зондовые методы, которые связаны с необходимостью введения различной толщины зондов. Такая процедура неприятна как для больного, так и для медперсонала и невозможна при исследовании соматически тяжелых больных, больных в раннем послеоперационном периоде и пр. Именно этой причиной объясняется непрекращающийся интерес физиологов и клиницистов к изучению и разработке новых методов, позволяющих не только качественно, но и количественно адекватно оценивать интенсивность и характер моторной активности различных отделов ЖКТ. В качестве дополнительных методов исследования моторно­эвакуатурной функции применяются методы, основанные на измерении электрической активности органов. Исследования биоэлектрической активности органов ЖКТ положили начало созданию нового метода исследования в медицине, получившего название электрогастроэнтерография. Электрогастроэнтерография — это метод исследования, позволяющий оценить биоэлектрическую активность желудка, двенадцатиперстной кишки и других отделов ЖКТ, который осуществляется посредством электрогастроэнтерограмм. Применение фрактального анализа к получаемым биоэлектрическим сигналам от органов позволяет эффективно судить об их моторной функции и успешно диагностировать различные заболевания.

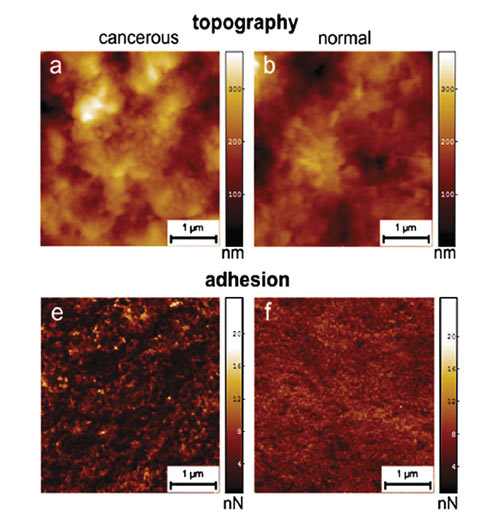
Необходимо упомянуть и о недавнем открытии американских ученых в области раковых заболеваний. Они показали, что если составить карты адгезии (от лат. adhaesio — прилипание, в физике — сцепление поверхностей разнородных твердых и/или жидких тел) поверхностей нормальных и раковых клеток, то окажется, что эти карты имеют разную фрактальную размерность (рис. 6). Возможно, это открытие в будущем поможет разработать новые эффективные методы диагностики и лечения онкологических заболеваний.

Рис. 6. Карты адгезии нормальных и раковых клеток

Применение фракталов в естественных науках

Применение фракталов в естественнонаучных дисциплинах чрезвычайно важно. Не хватит и целой книги, если попытаться описать всё, поэтому остановимся на некоторых самых интересных аспектах.

Очень часто фракталы применяются в геологии и геофизике. Не секрет, что побережья островов и континентов имеют некоторую фрактальную размерность, зная которую можно очень точно вычислить их длину. Фрактальный анализ также помогает в поиске и разработке месторождений полезных ископаемых, распределение которых очень часто происходит по фрактальному механизму. Исследование разломной тектоники и сейсмичности порой тоже осуществляется с помощью фрактальных алгоритмов.

Геофизика использует фракталы и фрактальный анализ для исследования аномалий магнитного поля, для изучения распространения волн и колебаний в упругих средах, для исследования климата и многих других природных явлений.

В физике фракталы применяются еще шире. Например, в физике твердых тел фрактальные алгоритмы позволяют точно описывать и предсказывать свойства твердых, пористых, губчатых тел, различных аэрогелей. Это помогает в создании новых материалов с необычными и полезными свойствами.

Рис. 7. Турбулентность и кристаллы

Изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны, поэтому их сложно точно смоделировать. И здесь помогает переход к фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяет им лучше понять динамику сложных систем (рис. 7). При помощи фракталов также можно смоделировать языки пламени. Пористые материалы хорошо представляются во фрактальной форме в связи с тем, что они имеют очень сложную геометрию. Это используется в науке о нефти.

Итак, проведя сей небольшой обзор, можно с уверенностью сказать об огромном практическом применении фракталов и фрактальных алгоритмов. Список областей, где применяются фракталы, очень широк, и в ближайшем будущем он будет только пополняться!

1Продолжение. Начало см. в КомпьюАрт № 12’2012, 1 и 2’2013.

Источник