предикаты первого порядка допускают присутствие в качестве параметров

Исчисление предикатов

Содержание

Исчисление предикатов [ править ]

Предикаты могут быть 0-местными, в этом случае это хорошо нам известные пропозициональные переменные, принимающие какие-то истинностные значения, в происхождение которых мы не вникаем.

Чтобы построить новое исчисление, нам требуется указать 3 компонента: язык, аксиомы и правила вывода.

Язык [ править ]

Добавим к языку исчисления высказываний новые конструкции с предикатами и получим язык исчисления предикатов. Вот расширенная грамматика:

Добавились 3 новых сущности:

(b) предикаты (они обобщили пропозициональные переменные)

(c) кванторы: всеобщности ( [math] \forall [/math] ) и существования ( [math] \exists [/math] ).

Аксиомы [ править ]

Определение:

Будем говорить, что переменная [math]y[/math] свободна для [math]x[/math] при подстановке в формулу [math]\psi[/math] (или просто свободна для подстановки вместо [math]x[/math] ), если после подстановки [math]y[/math] вместо свободных вхождений [math]x[/math] ни одно ее вхождение не станет связанным.

(11) [math]\forall(\psi) \rightarrow (\psi[x := \alpha]) [/math]

(12) [math](\psi[x := \alpha]) \rightarrow \exists(\psi) [/math]

Пример, когда нарушение свободы для подстановки приводит к противоречию:

[math] \forall(\psi) \to (\psi[x := \alpha]) \\ \psi := \exists a \lnot P(a) = P(b), x := b, \alpha := a \\ \forall b \exists a (\lnot P(a) = P(b)) \to \exists a (\lnot P(a) = P(a)) \\ [/math]

[math] \exists a (\lnot P(a) = P(a)) [/math]

Все аксиомы, порожденные данными схемами в новом языке, мы назовем аксиомами исчисления предикатов.

Правила вывода [ править ]

Добавив эти схемы к схеме для правила Modus ponens исчисления высказываний, мы сможем породить множество правил вывода.

Итог [ править ]

Определение:

Формальная система, составленная из указанного языка, множества аксиом и множества правил вывода, называется исчислением предикатов.

Обратите внимание на требование отсутствия свободных переменных в допущениях.

Доказательство:[math]\triangleright[/math]Упражнение.[math]\triangleleft[/math]

Доказательство разбором случаев. 3 старых случая те же, добавилось 2 новых правила вывода.

Источник

Предикаты первого порядка допускают присутствие в качестве параметров

9. ЛОГИКА ПРЕДИКАТОВ ПЕРВОГО ПОРЯДКА

9.1. Основы логики предикатов первого порядка

Логика предикатов первого порядка является дальнейшим развитием традиционной логики Аристотеля и логики высказываний. Одним из ключевых понятий логики высказываний является непосредственно высказывание – выражение, записанное с помощью определенного синтаксиса, которому можно приписать истинностное значение (истина или ложь). Например, выражения «В сутках 24 часа» или «Инопланетяне существуют» являются высказываниями, т.к. могут быть истинными или ложными (в зависимости от принятой объективной или субъективной точки зрения). При этом само выражение в логике высказываний представляется неделимым целым, т.е. его нельзя разделить на отдельные компоненты и, соответственно, использовать сведения об его структуре.

Предикат первого порядка часто называют атомарной формулой (атомом), что означает неделимость предиката на подформулы, эквивалентные по своей семантике другому предикату. Номер порядка (первый) означает, что в качестве термов нельзя использовать другие предикаты. В то же время за счет использования логических операций (связок) предикаты можно объединять в более сложные высказывания.

Таким образом, обладая всеми достоинствами логики высказываний, логика предикатов позволяет получить доступ к отдельным частям атомарных выражений, что, в свою очередь, расширяет возможности логического вывода.

1 В логике предикатов, с синтаксической точки зрения, под «символом» понимается, как одиночный символ, так и их набор.

9.2. Синтаксис и семантика логики предикатов первого порядка

Синтаксис и семантика логики предикатов первого порядка [2, 23, 31]:

— логическая константа – true (истина) и false (ложь);

— константа – символьное выражение, начинающееся со строчной буквы (например, cat, blue);

— переменная – символьное выражение, начинающееся с прописной буквы или знака подчеркивания (например, X, Сat, _blue);

— функция и предикат – символьное выражение, начинающееся со строчной буквы, за которым следует список аргументов (термов), заключенных в скобки (например, кошка(катя), sin(X), друзья(вася, петя)). Отличие функции от предиката, заключается в том, что функция возвращает результаты любого типа (строку, число, дату и т.д.), а предикат – только логического типа (истину или ложь);

— список – упорядоченный набор элементов (констант, переменных или предикатов), указанных через запятую и заключенных в квадратные скобки (например, [red, blue], [X, Сat, _blue], [кошка(катя)]);

— терм – константа, переменная, функция или список;

— ∨ – логическое ИЛИ (дизъюнкция, логическое сложение);

При вычислении составных формул приняты правила вывода, показанные в табл.8.1.

Приоритет операций и кванторов при исчислении формул показан ниже.

В скобках показаны операции (кванторы) с одинаковым приоритетом. Если в формуле используются операции (кванторы) с одинаковым приоритетом, то порядок исчисления слева-направо. Изменение порядка исчисления можно добиться за счет использования круглых скобок «( )».

— если Маша мать X и Y, то X является братом или сестрой Y:

мать(маша, X) ∧ мать(маша, Y) → брат(X, Y) ∨ сестра(X, Y).

— если X – человек, то он смертен:

Квантор существования ∃ указывает, что предложение истинно, по крайней мере, для одного значения переменной. Например, ∃X друзья(X, петя) – существует, по крайней мере, один субъект X, который является другом Пети.

Квантор всеобщности ∀ указывает, что предложение истинно, для всех значений переменной. Например, ∀X человек(X) → смертен(Х) – все люди смертны.

При комбинации кванторов очень важен порядок их использования, например [22]:

— ∀X∃Y любит(Х, Y) – любой Х любит хотя бы одного Y;

— ∀Y∃X любит(Х, Y) – любого Y любит хотя бы один Х;

— ∃X∀Y любит(Х, Y) – существует такой Х, который любит всех Y;

— ∃Y∀X любит(Х, Y) – существует такой Y, которого любят все X;

— ∀X∀Y любит(Х, Y) и ∀Y∀Х любит(Х, Y) – любой X любит всех Y и любой Y любим всеми X (эквивалентные предложения);

— ∃X∃Y любит(Х, Y) – существует такой X, который любит хотя бы одного из Y;

— ∃Y∃Х любит(Х, Y) – существует такой Y, которого любит хотя бы один X.

9.3. Исчисление предикатов

Исчисление предикатов использует для вывода те же правила, что и классическое исчисление высказываний: правило Modus Ponens и правило подстановки.

Основными отличиями логики предикатов от логики высказываний являются:

— использование в формулах кванторов;

— использование в формулах предикатов и функций;

— логика высказываний: «Я человек» → «Я смертен»;

Для доказательства целевого утверждения (гипотезы) в Прологе используется метод перебора с возвратами (поиск в глубину). В тоже время, за счет структуры и порядка формул можно добиться реализации поиска в ширину.

9.4. Достоинства и недостатки логики предикатов первого порядка

Достоинства логики предикатов первого порядка [21]:

— в качестве «фундамента» используется классический аппарат математической логики, методы которой достаточно хорошо изучены и формально обоснованы;

— в базах знаний можно хранить лишь множество аксиом, а все остальные знания получать из них по правилам вывода.

Недостатки логики предикатов первого порядка [4, 23]:

— требуется адекватное описание предметной области, т.е. в базе знаний должна быть представлена вся информация, необходимая для решения задачи;

— невозможность применения в качестве термов (параметров) предикатов других предикатов, т.е. невозможность формулирования знаний о знаниях.

Источник

6. Исчисление предикатов

Рассмотрим построение теории первого порядка.

Компонентами теории первого порядка являются следующие.

1. Алфавит составляют:

· Предметные константы – буквы начала латинского алфавита с натуральными индексами: , , …, , , … Предметные символы – это имена (обозначения) предметов.

· Предметные переменные – буквы конца латинского алфавита с натуральными индексами: , , …, , , …

· Функциональные буквы – строчные буквы латинского алфавита с натуральными индексами (верхний индекс указывает число переменных, нижний – номер функциональной буквы): , , …

· Предикатные буквы – заглавные буквы латинского алфавита с натуральными индексами (верхний индекс указывает число переменных, нижний – номер предикатной буквы): , , . (индексы можно не указывать).

· Логические связки: .

· Квантор всеобщности .

· Синтаксические символы – скобки (, ) и запятая.

2. Формула определяется несколькими этапами. Вначале вводится понятие терма.

Определение. 1) Предметные константы и предметные переменные есть Термы.

2) Если , , …, , – термы, – функциональная буква, то – терм.

3) Символ является термом тогда и только тогда, когда это следует из 1) и 2).

Примеры. 1. Пусть – предметная переменная, – предметная константа, , – функциональные буквы. Тогда , – термы.

2. Пусть – предметная переменная, – предметная константа, , – функциональные буквы. Тогда , – термы. Здесь символы , имеют только формальный смысл и не интерпретируются как обозначения тригонометрических функций.

Определение. Если , , …, , – термы, – предикатная буква, то символ называется элементарной формулой.

Другими словами, элементарная формула образуется при применении предикатной буквы к термам.

Примеры. 1. В условиях первого примера, если – предикатная буква, то – элементарная формула.

2. В условиях второго примера, если – предикатная буква, то – элементарная формула.

Теперь определим формулу логики предикатов.

Определение. 1) Всякая элементарная формула есть формула.

2) Если , – формулы, то формулами являются также символы , , .

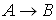
3) Символ является формулой тогда и только тогда, когда это следует из 1) и 2).

Примеры. 1. В условиях первого примера, – формула.

2. В условиях второго примера, – формула.

В теории первого порядка, как и в исчислении высказываний, допускаются формулы с другими логическими связками, а также допускается использование квантора существования. Известна формула (см. Глава 5. Предикаты.).

Здесь мы ненадолго отвлечемся от построения теории первого порядка и рассмотрим некоторые понятия, связанные с формулами.

Определение. Пусть – формула, – переменная, которая входит в формулу (один или несколько раз). Вхождение в формулу называется Связанным, если либо – переменная в кванторе (), либо находится в области действия квантора . Если вхождение в не связано, то оно называется свободным.

Пример. В формуле вхождения обеих переменных свободные.

В формуле вхождения переменной в посылку связаны, а вхождение в следствие свободно. Вхождение переменной свободно, так как отсутствует квантор .

В формуле вхождения обеих переменных связаны.

Пусть – формула, – переменная в формуле , – терм. Введем обозначение . Тогда – результат подстановки вместо всех свободных вхождений в формулу .

Пример. Рассмотрим подстановку вместо всех свободных вхождений в формулы из предыдущего примера.

В формуле вхождение свободное, следовательно, получаем .

В формуле вхождения переменной в посылку связаны, а вхождение в следствие свободно. Получаем: .

В формуле вхождения обеих переменных связаны, поэтому осуществить подстановку невозможно.

Определение. Терм называется свободным для переменной в формуле тогда и только тогда, когда никакое свободное вхождение в формулу не лежит в области действия квантора , где – переменная в терме .

Пример. Рассмотрим формулу и терм . не свободен для переменной в данной формуле, так как лежит в области действия квантора, тем более не свободен для переменной .

Пусть теперь дан терм . свободен для переменной .

Уточним понятие интерпретации для множества формул теории первого порядка.

Определение. Интерпретацией множества формул называется область интерпретации и заданное на ней соответствие, которое каждой предикатной букве ставит в соответствие -местный предикат на , каждой функциональной букве – -местную функцию на , каждой предметной константе – элемент множества .

При интерпретации формулы превращаются в предикаты на множестве . Если формула не имеет свободных переменных, то после интерпретации она превращается в высказывание.

Пример. На множестве рассмотрим формулу . Интерпретируем эту формулу следующим образом: . Тогда мы получим предикат .

Рассмотрим теперь формулу . При интерпретации она превращается в истинное высказывание .

Определение. Интерпретация называется Моделью формальной теории (или некоторого множества формул), если все формулы формальной теории (или множества формул) истинны в данной интерпретации.

Определение. Формула называется Общезначимой (Логически общезначимой), если она истинна в любой интерпретации.

Определение. Формулы и называются Логически эквивалентными тогда и только тогда, когда формула логически общезначима.

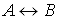
Справедлива теорема, аналогичная теореме из логики высказываний.

Теорема. Отношение логической эквивалентности является отношением эквивалентности.

Определение. Говорят, что формула Логически влечет формулу (из формулы Логически следует формула ), если формула является логически общезначимой.

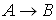
Теорема. Отношение логического следствия является отношением предпорядка.

Определение. Формула называется Противоречивой, если она ложна в любой интерпретации.

Теорема. Пусть – формула, – переменная в формуле , терм свободен для переменной в формуле . Тогда формула общезначима.

Доказательство. Пусть имеется некоторая интерпретация исходной формулы, то есть множество и – предикат на . Покажем, что – тождественно истинный предикат. Возьмем произвольный набор значений переменных . Подставим этот набор в предикат. Получим высказывание:

.

Покажем, что это высказывание истинно. Возможны два случая.

1. , следовательно .

2. .

Соотношение выполнено при любых значениях . Подставим этот набор значений в терм : . Подставим последнее выражение в предикат . Получим:

.

Но, поскольку терм свободен для переменной в формуле , получаем:

Следовательно, по свойству импликации получаем, что , что и требовалось доказать.

Теорема. Пусть не является свободной переменной в формуле , – некоторая формула. Тогда формула общезначима.

Доказательство аналогично доказательству предыдущей теоремы.

Теперь мы можем вернуться к построению теории первого порядка.

3. Аксиомы теории первого порядка делятся на два класса:

1) .

2) .

3) .

4) , где терм свободен для переменной в формуле .

5) , где – несвободная переменная в формуле .

Отметим, что аксиомы 1) – 3) – тавтологии, 4) и 5) – общезначимые формулы.

У каждой теории первого порядка свои собственные аксиомы.

├.

2) Правило обобщения Gen.

├.

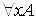
Определение. Теория первого порядка без собственных аксиом называется исчислением предикатов первого порядка (или чистым исчислением предикатов).

Без доказательства приведем теоремы.

Теорема. Всякая теорема исчисления предикатов логически общезначима, то есть исчисление предикатов непротиворечиво.

Теорема о полноте. Всякая логически общезначимая формула является теоремой исчисления предикатов.

Рассмотрим несколько примеров теорий первого порядка с собственными аксиомами, (приведем только собственные аксиомы). Для удобства вместо предикатных и функциональных букв будем записывать привычные символы.

Источник