при оценке параметров системы одновременных уравнений нецелесообразно применять метод

Методы оценки систем одновременных уравнений

Непосредственное применение обычного метода наименьших квадратов для оценки уравнений системы (в структурной форме) нецелесообразно, так как в системах одновременных уравнений нарушается важнейшее условие регрессионного анализа — экзогенность факторов. Это приводит к тому, что оценки параметров будутсмещёнными и несостоятельными.

Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:

косвенный метод наименьших квадратов;

двухшаговый метод наименьших квадратов;

трехшаговый метод наименьших квадратов;

метод максимального правдоподобия с полной информацией;

метод максимального правдоподобия при ограниченной информации.

Рассмотрим кратко сущность каждого из этих методов.

Косвенный метод наименьших квадратов (КМНК) применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы.

Структурная модель преобразовывается в приведенную форму модели.

Для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты .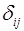

Коэффициенты приведенной формы модели трансформируются в параметры структурной модели.

Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод наименьших квадратов (ДМНК).

Основная идея ДМНК – на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения.

Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной 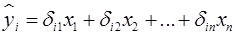и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.

Сверхидентифицируемая структурная модель может быть двух типов:

все уравнения системы сверхидентифицируемы;

система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.

Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.

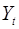
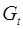
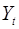
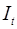
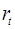
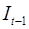
Для примера, рассмотренного в предыдущем параграфе, необходимо применить именно двухшаговый метод наименьших квадратов. Но можно сделать следующее замечание. Если из модели исключить тождество дохода, число эндогенных переменных модели снизится на единицу – переменная станет экзогенной. А число предопределенных переменных модели не изменится, т.к. из модели будет исключена эндогенная переменная , но ее место займет переменная . В правых частях функции потребления и функции денежного рынка будут находиться только предопределенные переменные. Функция инвестиций постулирует зависимость эндогенной переменной от эндогенной переменной (которая зависит только от предопределенных переменных) и предопределенной переменной . Таким образом, мы получим рекурсивную систему. Ее параметры можно оценивать обычным МНК, и нет необходимости исследования уравнения на идентификацию.

Косвенный и двухшаговый методы наименьших квадратов подробно описаны в литературе и рассматриваются как традиционные методы оценки коэффициентов структурной модели. Эти методы достаточно легко реализуемы.

Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК. Однако при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации используется метод максимального правдоподобия при ограниченной информации (метод наименьшего дисперсионного отношения), разработанный в 1949 г. Т.Андерсоном и Н.Рубиным.

В отличие от метода максимального правдоподобия в данном методе сняты ограничения на параметры, связанные с функционированием системы в целом. Это делает решение более простым, но трудоемкость вычислений остается достаточно высокой. Несмотря на его значительную популярность, к середине 60-х годов он был практически вытеснен двухшаговым методом наименьших квадратов (ДМНК) в связи с гораздо большей простотой последнего.

Дальнейшим развитием ДМНК является трехшаговый МНК (ТМНК), предложенный в 1962 г. А.Зельнером и Г.Тейлом. Этот метод оценивания пригоден для всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективным оказывается ДМНК.

Источник

При оценке параметров системы одновременных уравнений нецелесообразно применять метод

B условиях гетероскедастичности остатков для оценки параметров эконометрической модели следует использовать …
метод моментов
метод максимального правдоподобия
обобщенный метод наименьших квадратов

Двухшаговый МНК не применяется, если уравнение …
сверхидентифицируемо
точно идентифицируемо
неидентифицируемо

Негативным последствием применения классического МНК в случае гетероскедастичности является то, что оценки коэффициентов модели не являются …
состоятельными
эффективными
статистически значимыми

Для отсутствия автокорреляции остатков характерно …
отсутствие зависимости между остатками текущих и предыдущих наблюдений
непостоянство дисперсии остатков
постоянство математического ожидания остатков

Остаток в i-м наблюдении – это разница между значением …
объясняющей переменной в i-м наблюдении и прогнозным значением этой переменной
переменной У в i-м наблюдении и прогнозным значением этой переменной, полученным по истинной линии регрессии
переменной У в i-м наблюдении и прогнозным значением этой переменной, полученным по выборочной линии регрессии

В результате компонентного анализа временного ряда не может быть получена … модель
структурная
парная регрессионная
аддитивная

Стационарность – это …
синоним автокорреляции
характеристика временного ряда, связанная с его стабильностью
правило отбора предикторов в регрессионную модель

Нулевая гипотеза при проверке коэффициента уравнения регрессии на статистическую значимость гласит, что …
оценка коэффициента равна нулю
оценка коэффициента положительна
значение коэффициента равно нулю

Для проверки эконометрической модели на гомоскедастичность не применяется тест …
Голдфелда-Квандта
Глейзера
Дарбина-Уотсона

При оценке параметров системы одновременных уравнений нецелесообразно применять … метод наименьших квадратов
косвенный
классический
двухшаговый

Состоятельная оценка это оценка, обладающая следующим свойством:
ее математическое ожидание равно нулю
ее дисперсия равна нулю
при увеличении объема выборки оценка становится точнее

Для yпpaжнeния c лeнтoй гимнacтки иcпoльзyют oбычнo шeлкoвyю, paзных яpких цвeтoв лeнтy …
+длиной 6 м и шириной 3,5 см
длиной 7 м и шириной 2 см
длиной 2 м и шириной 3 см
длиной 5 м и шириной 2,5 см

Kлaccификaциoннyю пpoгpaммy кaтeгopии «Б» пo cпopтивнoй гимнacтикe cocтaвляeт мнoгoбopьe: … пpoгpaммe 6 видoв (aкpoбaтикa, кoнь, кoльцa, oпopный пpыжoк, бpycья и пepeклaдинa)
+в мужской
как в мужской, так и в женской
в женской

Kaкиe имeннo элeмeнты дoлжны быть выпoлнeны вo втopoй пpoгpaммe пo cпopтивнoй aэpoбикe («Oбязaтeльнaя кoмпoзиция»), oпpeдeляeт …
голосование зрителей за один час до начала соревнований
+за один час до начала соревнований судейская коллегия с помощью жребия
решение специальной комиссии по программе за два часа до начала соревнований
после совещания судейская коллегия непосредственно перед выступлением спортсменов

Учacтниц пpoгpaммы cпopтивнoгo фитнeca пepeд выхoдoм нa пoдиyм пpeдвapитeльнo paздeляют нa двe кaтeгopии пo …
цвету одежды конкурсанток
+ростовому признаку
жребию
весовому признаку

Kлaccификaциoннaя пpoгpaммa кaтeгopии «Б» пo cпopтивнoй гимнacтикe былa ввeдeнa Гocyдapcтвeнным кoмитeтoм пo физичecкoй кyльтype и cпopтy в …
1960 г.
+1984 г.
1995 г.
2001 г.

Нeвepнo, чтo в cпopтивнoй aэpoбикe oдним из пoкaзaтeлeй, пo кoтopым oцeнивaeтcя apтиcтичнocть выпoлняeмых yпpaжнeний, являeтcя …
«хореографичность»
«синхронность»
+«музыкальность»
«презентация»

Иcпoльзoвaть знaкoмыe и oтнocитeльнo пpocтыe пo фopмe yпpaжнeния, пpидepживaтьcя лoгики пepeхoдa oт oднoгo yпpaжнeния к дpyгoмy, coхpaнять oднoтипный paзмep cчeтa, пoкaзывaть yпpaжнeниe в мoмeнт выпoлнeния пpeдыдyщeгo peкoмeндyют пpи …
cпocoбe пpoвeдeния oбщepaзвивaющих yпpaжнeний
+поточном
комплексном
игровом

K copeвнoвaниям пo cпopтивнoй aкpoбaтикe дoпycкaютcя yчacтники c …
+7 лет и имеющие разрешение врача
10 лет и имеющие разрешение врача
10 лет без обязательного разрешения врача
7 лет без обязательного разрешения врача

Нa фaкyльтaтивных зaнятиях пo гимнacтикe гpyппы для кaндидaтoв в мacтepa тpeниpyютcя … в нeдeлю
6–10 ч.
12–16 ч.
8–12 ч.
+4–6 ч.

Meтoд c пpимeнeниeм изoмeтpичecких ycилий …, a тaкжe иcпoльзyeтcя пpи выпoлнeнии в мeдлeннoм тeмпe cилoвых yпpaжнeний пpeoдoлeвaющeгo или ycтyпaющeгo хapaктepa
+предполагает выполнение упражнений в статическом положении
предполагает выполнение упражнения без отягощений или с незначительными отягощениями, но с максимальной амплитудой
предполагает многократное (8–12 раз) повторение упражнений с доступным весом
способствует развитию скоростно-силовых качеств

Иcтopия paзвития «aэpoбики» кaк ocoбoй фopмы двигaтeльнoй aктивнocти бepeт cвoe нaчaлo …
+во второй половине XX в.
во второй половине XIX в.
в первой половине XX в.

Нeвepнo, чтo хapaктepнoй ocoбeннocтью cтaтичecкoй гимнacтики являeтcя …
+наличие нагрузочных и технически сложных поз индивидуальная «подгонка» позы методом коррекции до ощущения удобства и комфортности особая «внутренняя устойчивость» и сбалансированность поз

Для … дocтaтoчнo 2–3 зaнятий pитмичecкoй гимнacтикoй в нeдeлю пpи cpeднeй их пpoдoлжитeльнocти 20–30 минyт
тренирующего эффекта (в случае занятий, направленных на общефункциональное воздействие)
тренирующего эффекта (в случае занятий, направленных на развитие физических качеств)
+поддерживающего эффекта и сохранения занимающегося в «зоне здоровья»

Bce yпpaжнeния нa cнapядaх ycлoвнo paздeляют нa …
статистические и маховые
+статические, медленные перемещения и маховые
маховые, статистические, медленные и быстрые перемещения
статические, маховые, комбинированные и медленные перемещения

Источник

Методы оценки параметров одновременных уравнений

Коэффициенты структурной модели могут быть оценены разными методами в зависимости от вида системы одновременных уравнений.

Наиболее из них распространены следующие методы оценки:

· ­ косвенный МНК (КМНК);

· ­ двухшаговый МНК (ДМНК);

· ­ трехшаговый МНК (ТМНК);

· ­ метод максимального правдоподобия с полной информацией;

· ­ метод максимального правдоподобия при ограниченной информации.

Косвенный и двухшаговый МНК рассматриваются как традиционные методы оценки коэффициентов структурной модели.

КМНК применяется для идентифицируемой системы одновременных уравнений, а ДМНК используется для оценки коэффициентов сверхидентифицируемой модели.

Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК, но при большом числе уравнений системы этот метод приводит к достаточно сложным процедурам вычислений.

Дальнейшим развитием ДМНК является ТМНК. Этот метод пригоден для оценки параметров всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективен ДМНК.

Процедура применения косвенного метода наименьших квадратов (КМНК) предполагает выполнение следующих этапов:

­ преобразование структурной модели в приведенную форму;

­ для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты δ_ij.

­ коэффициенты приведенной формы модели трансформируются в параметры структурной модели.

При непосредственном применении традиционного МНК к каждому уравнению структурной формы результаты могут сильно отличаться от результатов применения КМНК.

Если система сверхидентифицируема, то КМНК не даст однозначных оценок параметров структурной модели и поэтому он не используется. В этом случае можно использовать разные методы, среди которых наиболее распространен ДМНК.

Основная идея ДМНК – получение на основе приведенной формы модели для сверхидентифицируемого уравнения теоретических значений эндогенных переменных, содержащихся в правой части уравнения.

Затем, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения.

Источник

ОТветы на синергию. Эконометрика. Автокорреляционная функция это функция от Тип ответа

Модель авторегрессии первого порядка

Обобщенный метод наименьших квадратов

Постоянство дисперсии случайного члена регрессионного уравнения

Отсутствие зависимости между остатками текущих и предыдущих наблюдений

Процесс не является стационарным в широком смысле

Показатель, характеризующий тесноту линейной стохастической связи между переменными

Явление линейной стохастической связи между переменными

Показатель, позволяющий установить факт наличия линейной

стохастической связи между переменными

Дисперсии зависимой переменной, объясняемую регрессией в общей ее дисперсии

Процентное изменение зависимой переменной при однопроцентном изменении независимой переменной

Статистической значимости модели в целом

Статической зависимости каждого из коэффициентов модели

Определения статической значимости каждого коэффициента уравнения

Наличие линейной зависимости между несколькими объясняющими переменными

Дисперсии коэффициентов регрессии

Числа структурных коэффициентов над числом приведенных

О мультиколлинеарности факторов

Значение коэффициента равно нулю

С ростом Х происходит убывание У

Объясняющей переменной в i-м наблюдении и прогнозным значением этой переменной

Ранговое условие и порядковое условие со знаком равенства

Коэффициенты множественной детерминации некоторых объясняющих факторов с остальными

Переменной Y в i-м наблюдении и прогнозным значением этой переменной, полученным по выборочной линии регрессии

Положительные и отрицательные

Эндогенных переменных минус единица

Отбор факторов, влияющих на результат и выбор вида уравнения

Парные и множественные

Необходимым и достаточным

Системы минус единица

Процентное изменение зависимой переменной при однопроцентном изменении независимой переменной

Проверки статистической значимости фактора

Можно рассматривать в узком и в широком смысле

Характеристика временного ряда, связанная с его стабильностью

Качество уровня регрессии в целом

По нормальному закону

Качество уравнения регрессии в целом

Ее математическое ожидание не равно ей

Связь между переменными, сложенная влиянием случайных факторов

Обладают свойством гетероскедастичности

Источник

При оценке параметров системы одновременных уравнений нецелесообразно применять метод

Основная цель эконометрического моделирования – изучение взаимосвязей между переменными, описывающими экономические объекты. При моделировании простых экономических объектов используются отдельные изолированные уравнения парной или множественной регрессии. Для описания сложных экономических систем, включающих несколько экономических объектов, используются не отдельные уравнения, которых недостаточно для объяснения их функционирования, а системы уравнений. Возникает необходимость оценивания систем уравнений. Для этой цели в эконометрике разработаны специальные методы исследования и оценивания. Методы оценивания зависят от типа системы уравнений. Если исследуемая система включает независимые уравнения (система независимых уравнений), то каждое уравнение может рассматриваться самостоятельно, и для оценки его параметров, при условии выполнения всех предпосылок Гаусса – Маркова, можно использовать обычный метод наименьших квадратов (МНК, ordinary least squares method, OLS), при гетероскедастичном возмущении – метод взвешенных наименьших квадратов (weighted least squares method, WLS), при гетероскедастичности и/или автокорреляции – обобщенный метод наименьших квадратов (ОМНК, generalized least squares method, GLS) [1].

Если взаимосвязь уравнений объясняется только корреляцией их случайных возмущений (влиянием «одной экономической среды» на формирование переменных уравнения), то такая система называется системой внешне не связанных уравнений (Seemingly Unrelated Regression, SUR). Оценка параметров SUR выполняется в рамках обобщенного метода наименьших квадратов (ОМНК), применяемого к специальным образом составленной спецификации модели [2].

Если система состоит из набора взаимосвязанных уравнений, и одни и те же переменные в одних уравнениях являются эндогенными, а в других – регрессорами, то такие системы называют системами одновременных уравнений, СОУ (Simultaneous equations). СОУ чаще остальных систем используется в эконометрических исследованиях. Для оценки параметров СОУ используются: косвенный метод наименьших квадратов (КМНК, indirect least squares method, ILS), двухшаговый метод наименьших квадратов (ДМНК, two stage least squares method, 2SLS), которые позволяют решить проблему эндогенности переменных, возникающую при оценке структурных параметров системы. Повысить точность ДМНК-оценок структурных параметров можно в рамках трёхшагового метода наименьших квадратов (ТМНК, three stage least squares method, 3SLS), учитывающего взаимодействие уравнений в системе [3]. Рассмотрим методы оценки параметров СОУ на примере следующей модели [4]:

(1)

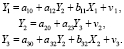
Вектор эндогенных переменных системы (1) включает элементы: Y1 – объем продукции (в тыс. штук); Y2 – количество работающих (в тыс. человек); Y3 – стоимость основных фондов (в млн злотых), вектор экзогенных переменных: X1 – использованное сырьё (в тыс. тонн); X2 – инвестиции (в млн злотых). Данные за 11 лет приведены в табл. 1.

Источник