prophet что за программа

Американцы создали самообучающуюся программу для исправления багов

Описание ошибки #53971 в коде PHP 5.3.3

Специалисты из Массачусетского технологического университета разработали программу Prophet, способную в полностью автоматическом режиме искать ошибки в исходном коде других программ и исправлять их. Согласно отчету авторов программы, для анализа и исправления программа использует стохастическую модель и способна к платформонезависимому применению исправлений кода. Prophet является значительно доработанной версией программы CodePhage.

Для работы с исходным кодом другого программного обеспечения Prophet использует данные об эффективных патчах, исходный код которых и описание опубликованы в открытых источниках в интернете. Для исправления ошибок алгоритм использует полученные из интернета и автоматически измененные патчи, причем он способен анализировать взаимодействие дописанного им самим исправленного кода с остальным кодом исправляемой программы.

Согласно утверждению разработчиков, в отличие от многих других программ для исправления кода, Prophet способен работать с исходным кодом программного обеспечения, состоящим не из нескольких сотен, а тысяч и десятков тысяч строк. При этом новый алгоритм способен к самообучению — при подборе патча к исправляемому программному обеспечению Prophet способен выбирать наиболее правильный код из множества вариантов, причем при выборе используется опыт предыдущих исправлений.

В основу алгоритма разработчики положили гипотезу о том, что у всех программ, независимо от языка, на котором они написаны, и платформы, для которой они предназначены, корректные участки кода имеют определенные универсальные признаки корректности, присутствующие на семантическом уровне. Prophet может составлять карту таких признаков корректности для изученных патчей, а затем переносить ее на анализируемый код программного обеспечения.

При работе с исходным кодом программы Prophet использует статический и динамический анализ кода, что позволяет не только выявить некорректные и потенциально нерабочие участки, но и локализовать ошибки с высокой точностью. Для выбора и изменения обнаруженных патчей и последующего их применения к программному коду также используется динамический анализ. Кроме того, как и Code Phage алгоритм Prophet способен «отмечать» потенциально опасные участки — при их исполнении с ошибкой исправленная программа просто закроется.

Тестирование Prophet раззработчики проводили на 69 известных ошибках в восьми программах с открытым исходным кодом. Результаты работы алгоритма сравнивали с другими такими программами — SPR, Kali, GenProg и AE. На анализ исходного кода и применение патчей всем испытуемым алгоритмам отводились 12 часов. За этот период Prophet сумел найти 19 патчей для 69 дефектов, 18 из которых оказались корректными. Причем 15 из 19 исправлений были подобраны алгоритмом с первой попытки.

В свою очередь SPR за 12 часов смогла найти только 16 правильных патчей из 19, причем только 11 корректных исправлений были подобраны с первой попытки. Kali, GenProg и AE сумели подобрать два, один и два корректных исправления соответственно.

Источник

Предсказываем будущее с помощью библиотеки Facebook Prophet

Прогнозирование временных рядов — это достаточно популярная аналитическая задача. Прогнозы используются, например, для понимания, сколько серверов понадобится online-сервису через год, каков будет спрос на каждый товар в гипермаркете, или для постановки целей и оценки работы команды (для этого можно построить baseline прогноз и сравнить фактическое значение с прогнозируемым).

Существует большое количество различных подходов для прогнозирования временных рядов, такие как ARIMA, ARCH, регрессионные модели, нейронные сети и т.д.

Сегодня же мы познакомимся с библиотекой для прогнозирования временных рядов Facebook Prophet (в переводе с английского, «пророк», выпущена в open-source 23-го февраля 2017 года), а также попробуем в жизненной задаче – прогнозировании числа постов на Хабрехабре.

Библиотека

Подробнее про алгоритмы можно прочитать в публикации Sean J. Taylor, Benjamin Letham «Forecasting at scale».

В этой же публикации представлено и сравнение mean absolute percentage error для различных методов автоматического прогнозирования временных рядов, согласно которому Prophet имеет существенно более низкую ошибку.

MAPE (mean absolute percentage error) — это средняя абсолютная ошибка нашего прогноза. Пусть — это показатель, а — это соответствущий этой величине прогноз нашей модели. Тогда — это ошибка прогноза, a — это относительная ошибка прогноза.

MAPE часто используется для оценки качества, поскольку эта величина относительная и по ней можно сравнивать качество даже на различных наборах данных.

Cтоит сказать пару слов о тех алгоритмах, с которыми сравнивали Prophet в публикации, тем более, большинство из них очень простые и их часто используют как baseline:

Практика

Установка

Данные

В качестве показателя для предсказания я выбрала количество постов, опубликованных на Хабрахабре. Данные я взяла из учебного конкурса на Kaggle «Прогноз популярности статьи на Хабре». Тут рассказано подробнее о соревновании и курсе машинного обучения, в рамках которого оно проводится.

Для начала посмотрим на данные и построим time series plot за весь период. На таком длинном периоде удобнее смотреть на недельные точки.

Построение прогноза

Для того чтобы измерить качество полученного прогноза, уберем из обучения последний месяц данных и будем предсказывать его. Создатели советуют делать предсказания по нескольким месяцам данных, в идеале – год и более (в нашем случае есть несколько лет истории для обучения).

Далее создаем объект класса Prophet (все параметры модели задаются в конструкторе класса, для начала возьмем default’ные параметры) и обучаем его.

В библиотеке Prophet есть встроенные средства визуализации, которые позволяют оценить результат построенной модели.

Во-первых, метод Prophet.plot отображает прогноз. Честно говоря, в данном случае такая визуализация не очень показательна. Основной вывод из этого графика, который я сделала — в данных много outlier ‘ов. Однако если при прогнозировании будет меньше исторических точек, то по ней можно будет что-нибудь понять.

На графике видно, что Prophet хорошо хорошо подстроился под рост числа постов «ступенькой» в начале 2015-го. По недельной сезонности можно сделать вывод, что меньше постов приходится на воскресенье и понедельник. На графике годовой сезонности ярче всего выделяется провал активности в Новогодние каникулы, также виден спад и на майских праздниках.

Оценка качества модели

Давайте оценим качество алгоритма и посчитаем MAPE для последних 30 дней, которые мы предсказывали. Для расчета нам нужны наблюдения и прогнозы для них .

Прежде чем продолжить, нам нужно объединить forecast с нашими исходными наблюдениями.

Напомню, что мы изначально отложили данные за последний месяц, чтобы построить прогноз на 30 дней и измерить качество получившейся модели.

Визуализация

Давайте сделаем свою визуализацию построенной Prophet модели: с фактическими значениями, прогнозом и доверительными интервалами.

Как видно, описанная выше функция позволяет гибко настраивать визуализацию и отобразить произвольное число наблюдений и прогнозов модели.

Визуально прогноз модели, кажется достаточно хорошим и разумным. Скорее всего такая низкая оценка качества объясняется аномальным высоким количеством постов 13 и 17 октября и снижением активности с 7 октября.

Также по графику можно сделать вывод, что большинство точек лежат внутри доверительного интервала.

Сравнение с ARIMA моделью

Стоит отметить, что построение ARIMA модели требует гораздо больших затрат по сравнению с Prophet : нужно исследовать исходный ряд, привести его к стационарному, подобрать начальные приближения и потратить немало времени на подбор гипер-параметров алгоритма (на моем компьютере модель подбиралась почти 2 часа).

Полезные ссылки

Немного материалов для более глубокого изучения библиотеки Prophet и предсказаний временных рядов, в общем:

Источник

ГЛАВА 6 Пакет prophet

Прогнозирование — это, пожалуй, самая распространенная задача, возникающая при работе с временными рядами. Однако получить надежные прогнозы непросто — для этого требуется серьезная подготовка специалиста, который решает подобную задачу, а также наличие подходящего (и желательно удобного в использовании) программного обеспечения.

В 2017 г. специалисты компании Facebook объявили о разработанном ими новом пакете для прогнозирования временных рядов — prophet (“пророк”). prophet во многом лишен указанных выше недостатков forecast и других подобных пакетов и позволяет создавать точные прогнозные модели в (полу–)автоматическом режиме. В этой главе мы рассмотрим основные возможности prophet и особенности работы с ним.

Пакет prophet распространяется бесплатно по лицензии MIT. Его легко установить стандартным образом из хранилища CRAN (на Windows–машинах предварительно нужно будет установить Rtools):

Если вы работаете на компьютере Mac под управлением OS X, не забудьте добавить аргумент type = «source» :

6.1 Методология

Оценивание параметров подгоняемой модели выполняется с использованием принципов байесовской статистики (либо методом нахождения апостериорного максимума (MAP), либо путем полного байесовского вывода). Для этого применяется платформа вероятностного программирования Stan. Пакет prophet представляет собой ни что иное, как удобный интерфейс для работы с этой платформой из среды R (имеется также аналогичная библиотека для Python — fbprophet ).

6.2 Первый простой пример

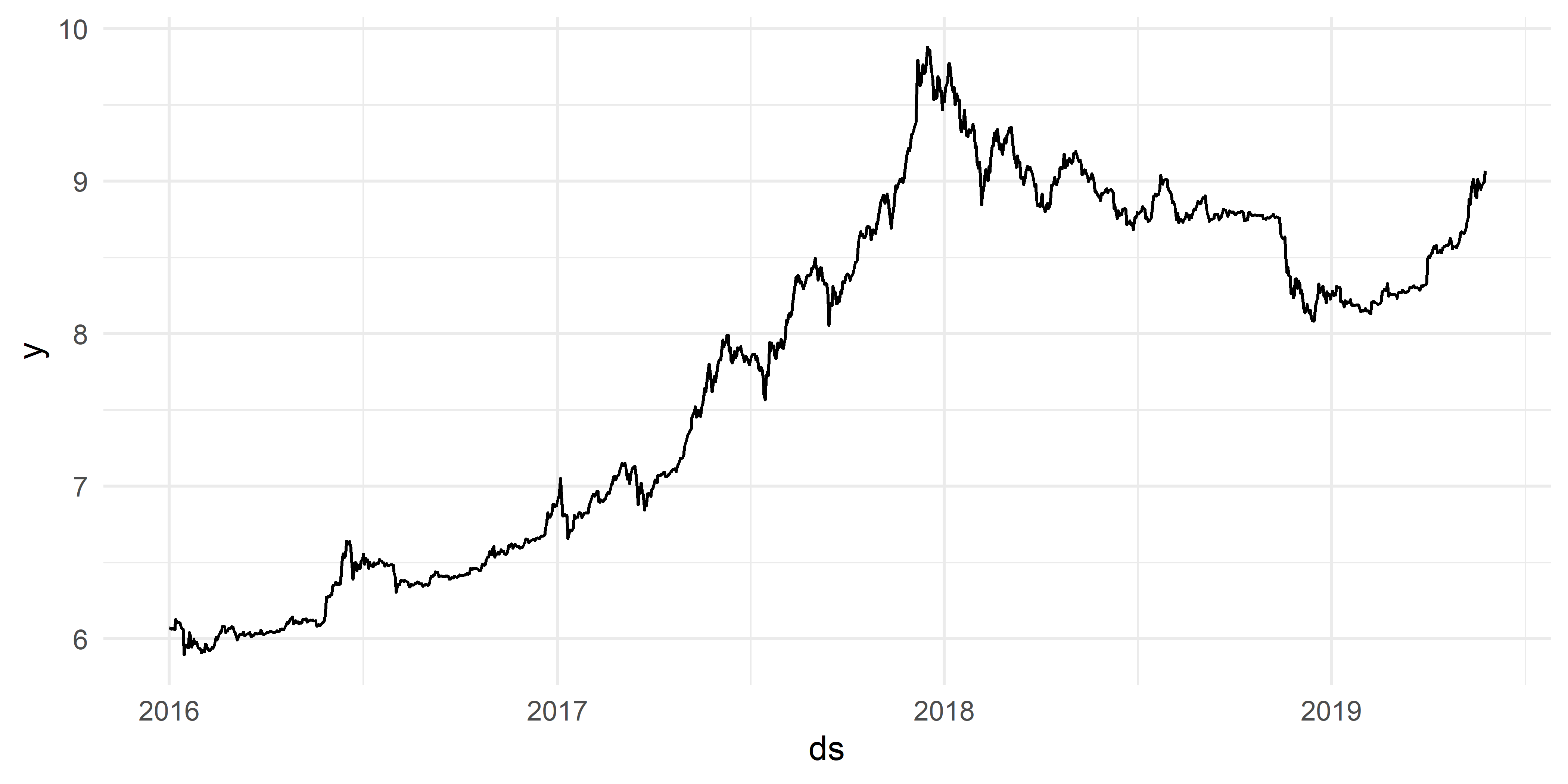
Предположим, что нам необходимо сделать прогноз стоимости биткоина на следующие 90 дней. Приведенный ниже код выполняет подготовку данных для построения подобной модели: сначала происходит логарифмирование значений стоимости биткоина y (для снижения дисперсии), а затем разбиение исходной выборки на обучающую (все наблюдения за исключением последних 90 дней) и проверочную (последние 90 дней).

Обучающие данные, подготовленные описанным выше способом, представлены на рис. 6.1.

РИСУНОК 6.1: Обучающие данные по стоимости биткоина

Нашу первую модель (обозначим ее M0 ) мы построим с использованием параметров, принятых в prophet по умолчанию. Для этого потребуется всего одна строка кода:

Объект forecast_M0 — это обычная таблица, в которой хранятся значения нескольких рассчитанных на основе модели M0 величин, включая компоненты модели (см. разд. 6.1), предсказанные значения отклика, а также верхние и нижние границы доверительных интервалов соответствующих величин. Вот так, например, выглядят первые несколько предсказанных значений стоимости биткоина и их (принятые по умолчанию) 80%–ные доверительные границы:

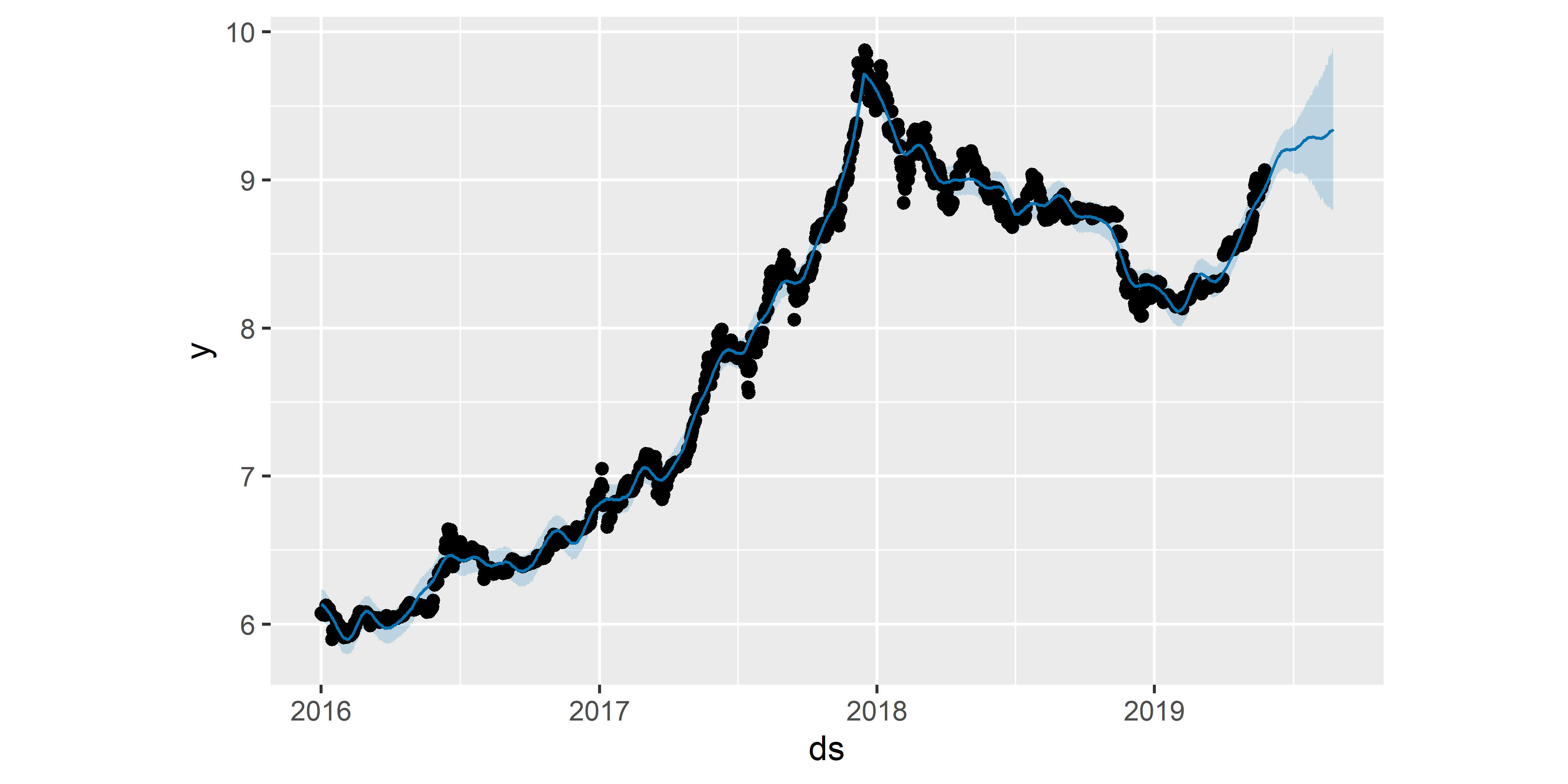
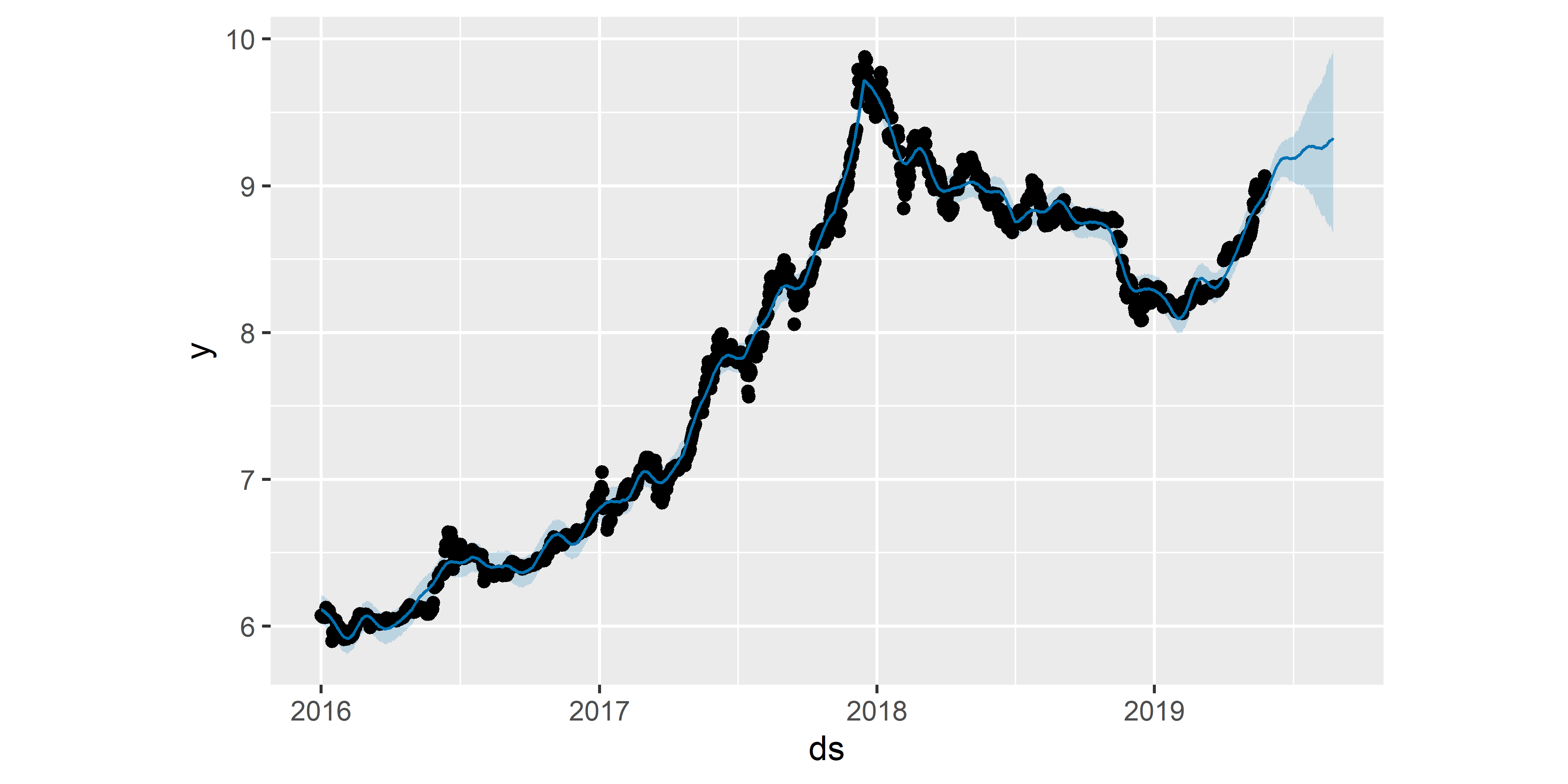
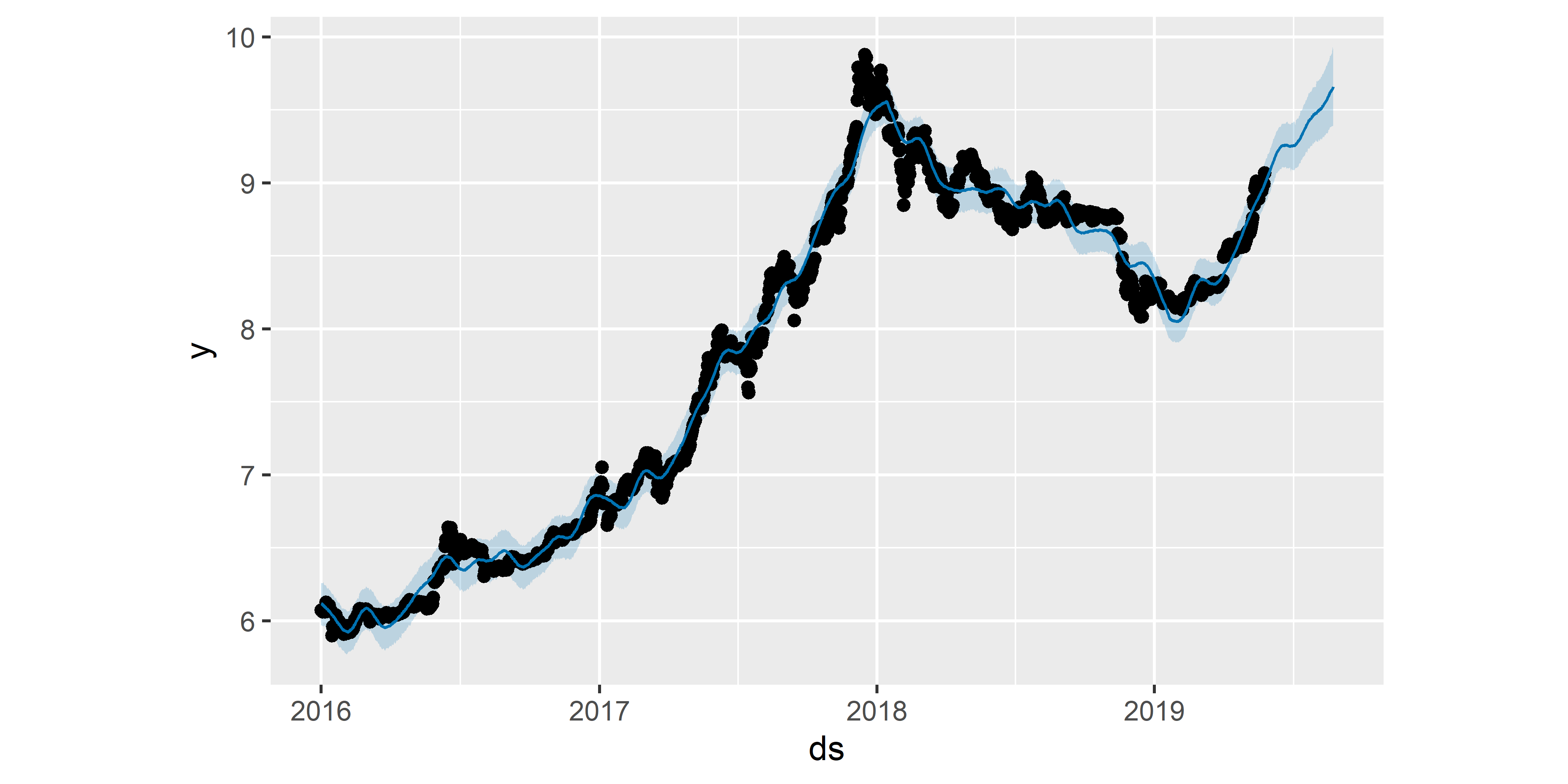
РИСУНОК 6.2: Прогноз стоимости биткоина, полученный на основе модели M0

Точки на рис. 6.2 соответствуют (логарифмированным) значениям стоимости биткоина из обучающей выборки. Сплошная голубая линия — это предсказанные моделью значения стоимости, а огибающая эту линию светло–голубая “лента” обозначает 80%–ные доверительные границы предсказанных значений. Прогнозные значения у на следующие 90 дней видны в правой части графика.

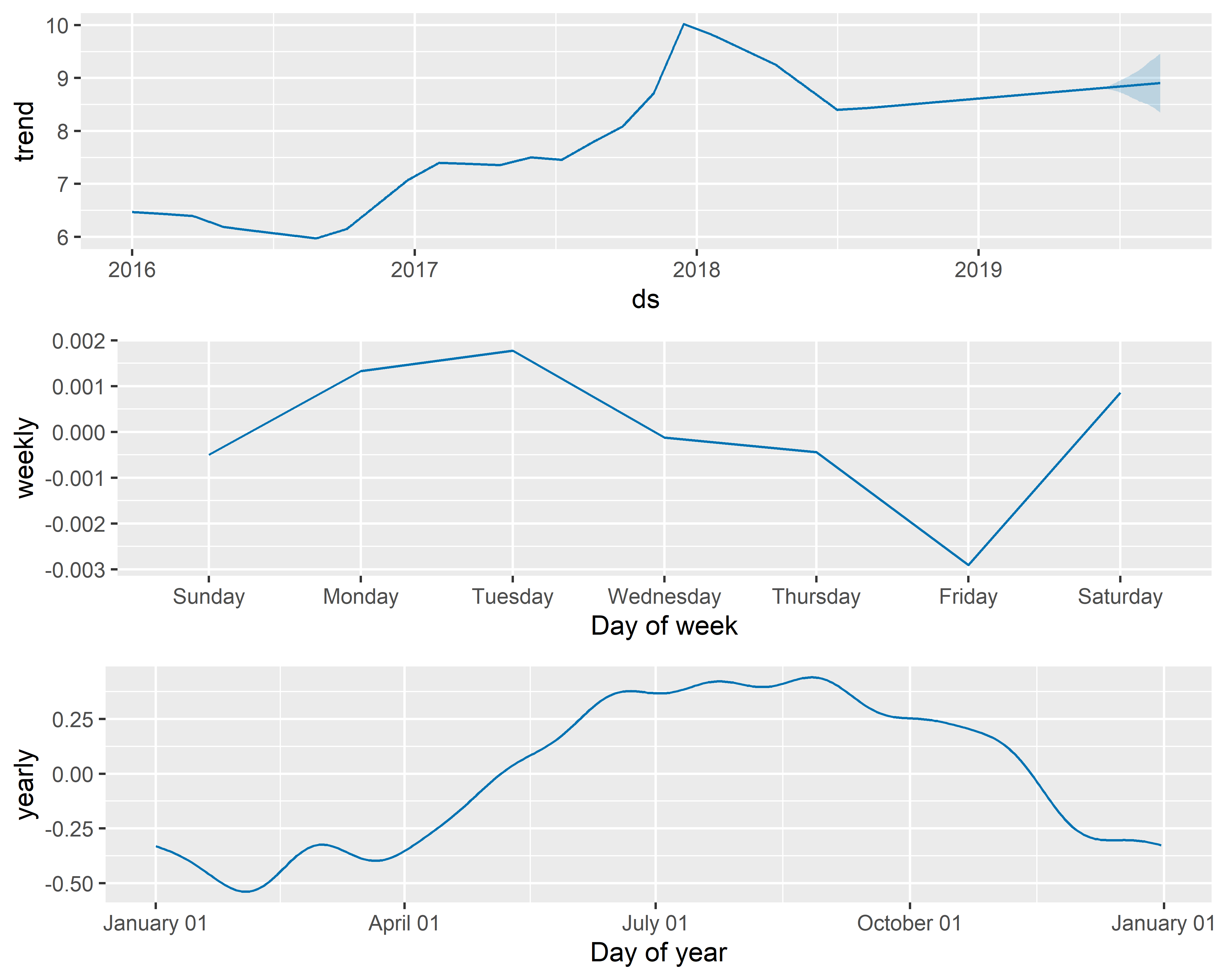
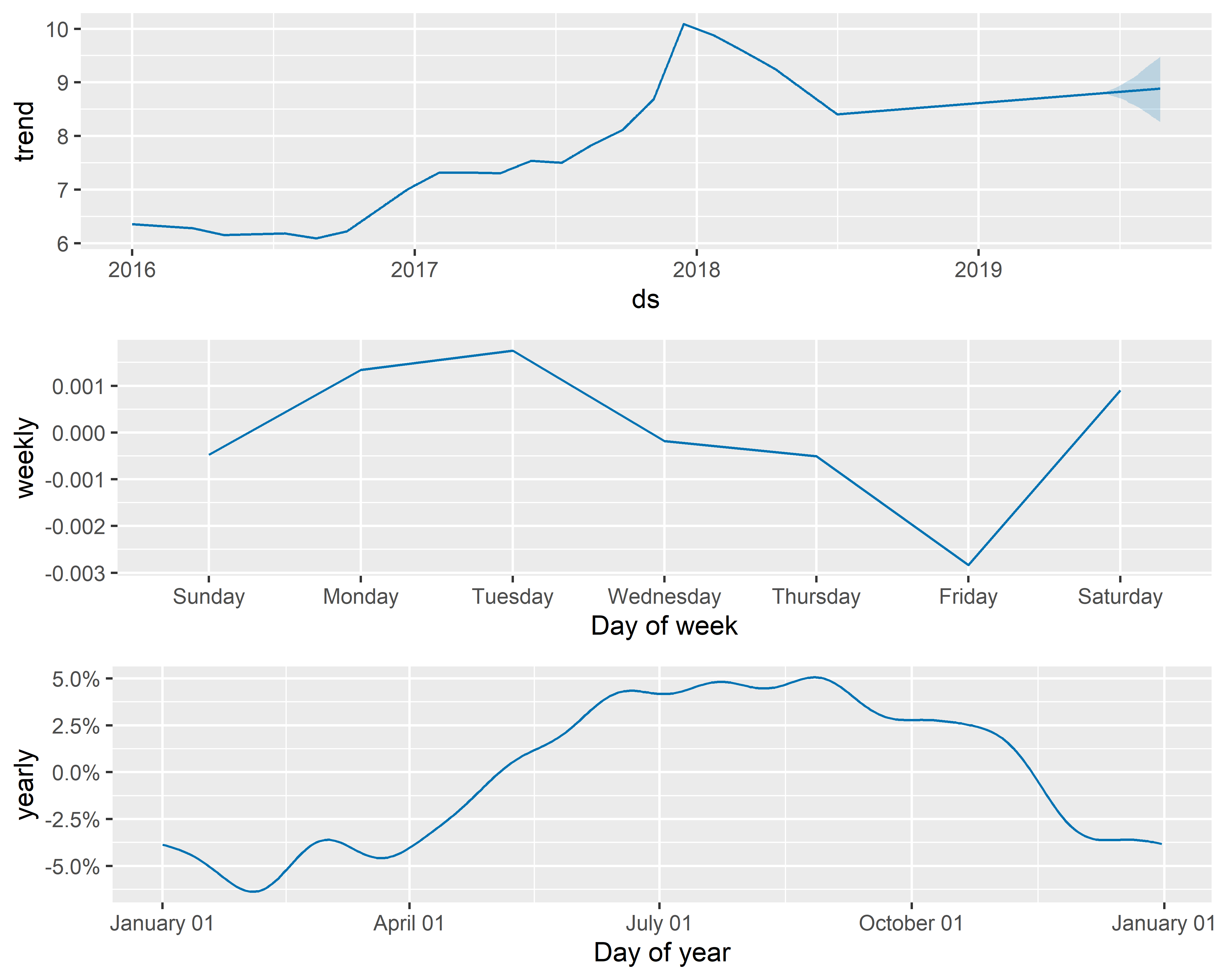
С помощью функции prophet_plot_components() мы можем также изобразить отдельные компоненты модели (рис. 6.3):

РИСУНОК 6.3: Компоненты модели M0

На рис. 6.3 видно, что модель M0 хорошо передает имеющийся в данных сложный тренд. Видно также, что в этом временном ряду есть очень слабо выраженные внутригодовые колебания и практически несуществующие колебания в пределах недели (обратите внимание на шкалы ординат этих трех графиков, которые помогают оценить вклад каждой из компонент).

6.3 Функция prophet()

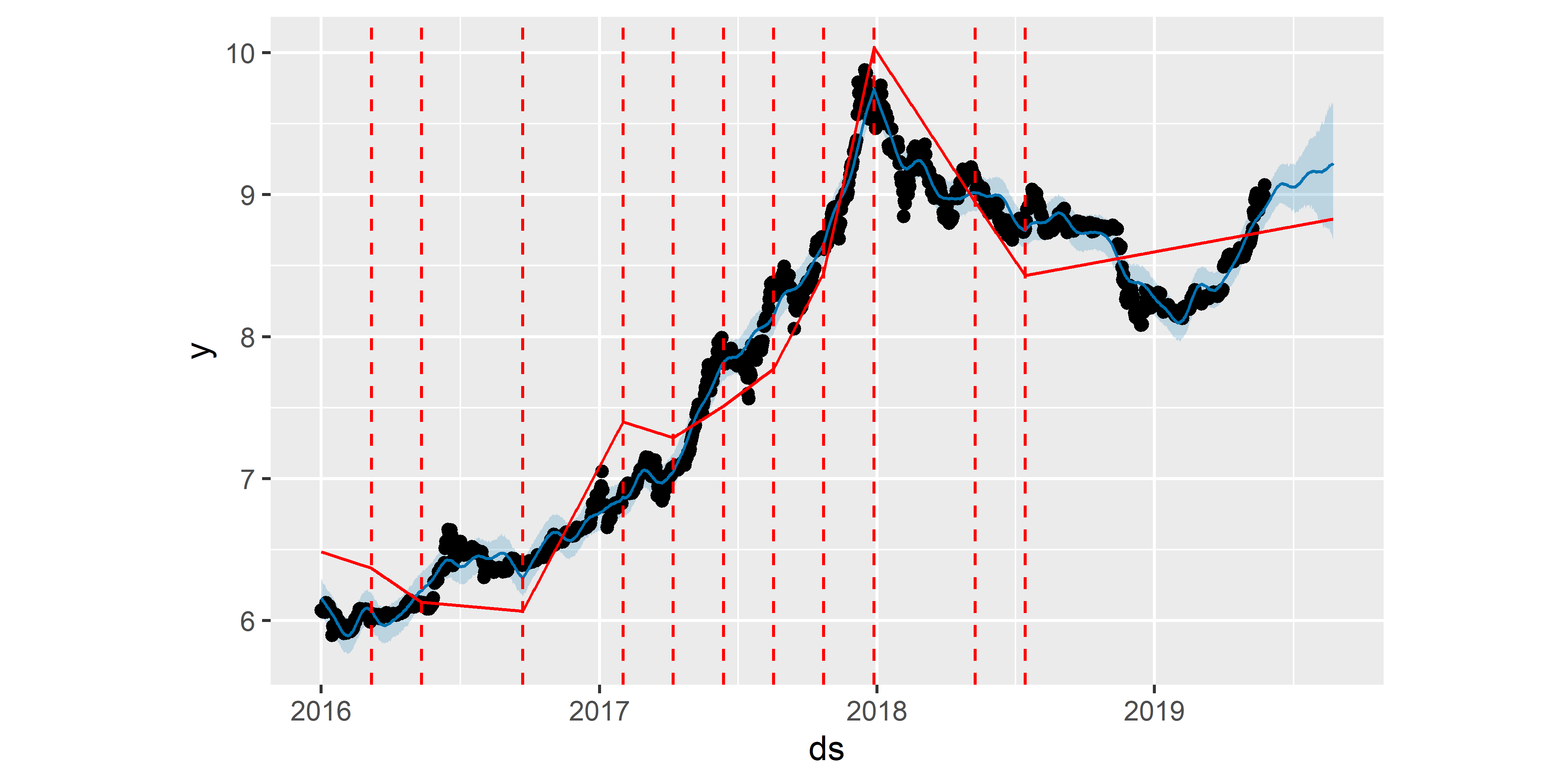
6.4 Точки излома тренда

Судя по полученному графику, модель M0 все еще переоценивает количество “переломных моментов” в тренде. Построим новую модель, которая будет инициализирована с меньшим начальным количеством потенциальных точек излома (15 вместо 25; рис. 6.5):

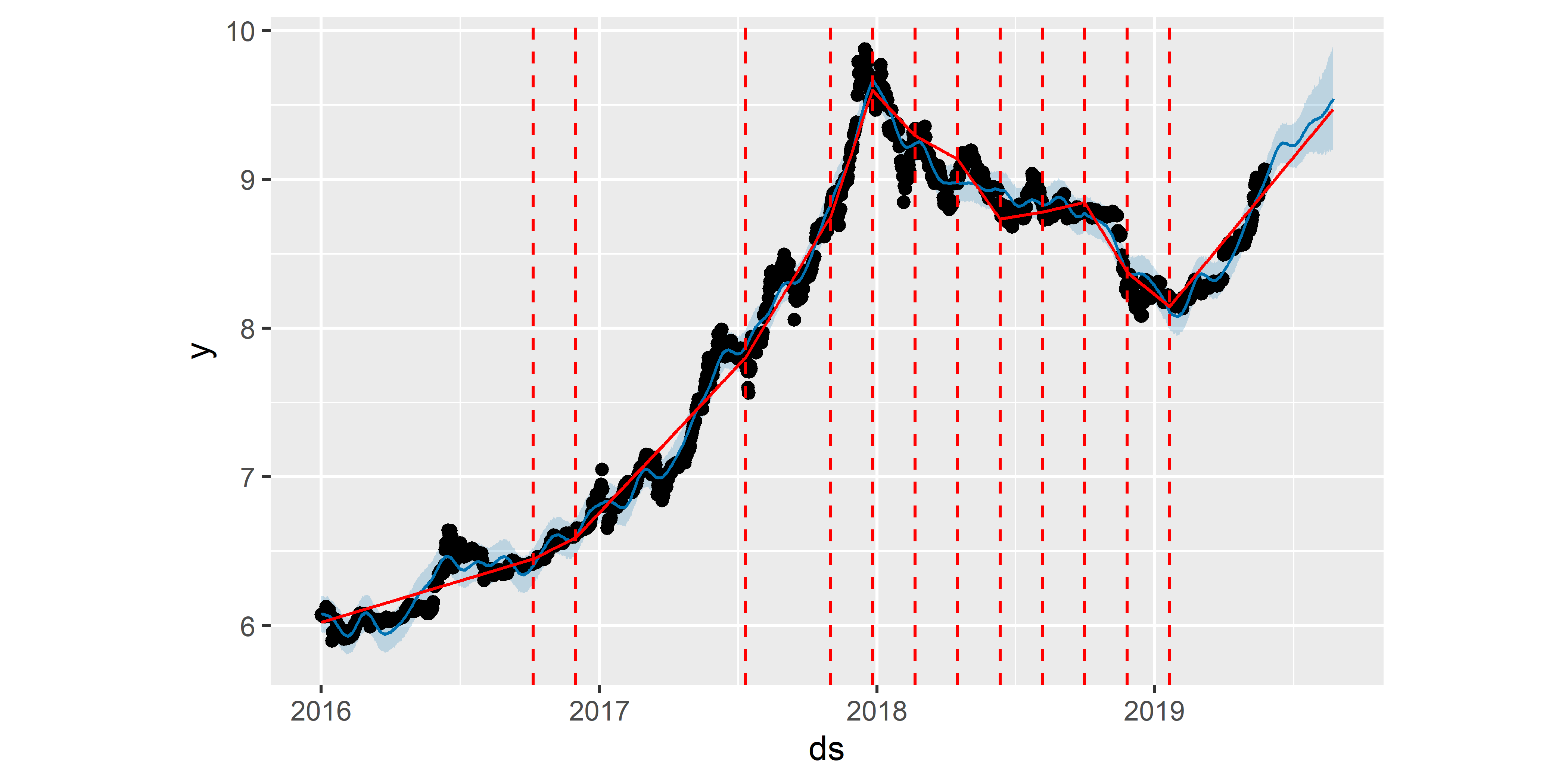
Помимо изменения начального количества потенциальных точек излома тренда мы можем также изменить временной интервал, в пределах которого происходит их оценивание. По умолчанию этот интервал охватывает первые 80% наблюдений. Однако из приведенных выше графиков видно, что примерно в начале ноября 2018 г. произошло резкое падение стоимости биткоина. Ни одна из построенных нами моделей пока не учла это изменение, поскольку оно не вошло в интервал, в пределах которого происходило оценивание точек излома. Увеличим этот интервал до 90%, воспользовавшись аргументом changepoint.range (одновременно увеличим количество потенциальных точек излома с 15 до 20, поскольку на большем промежутке времени можно ожидать больше перепадов в тренде):

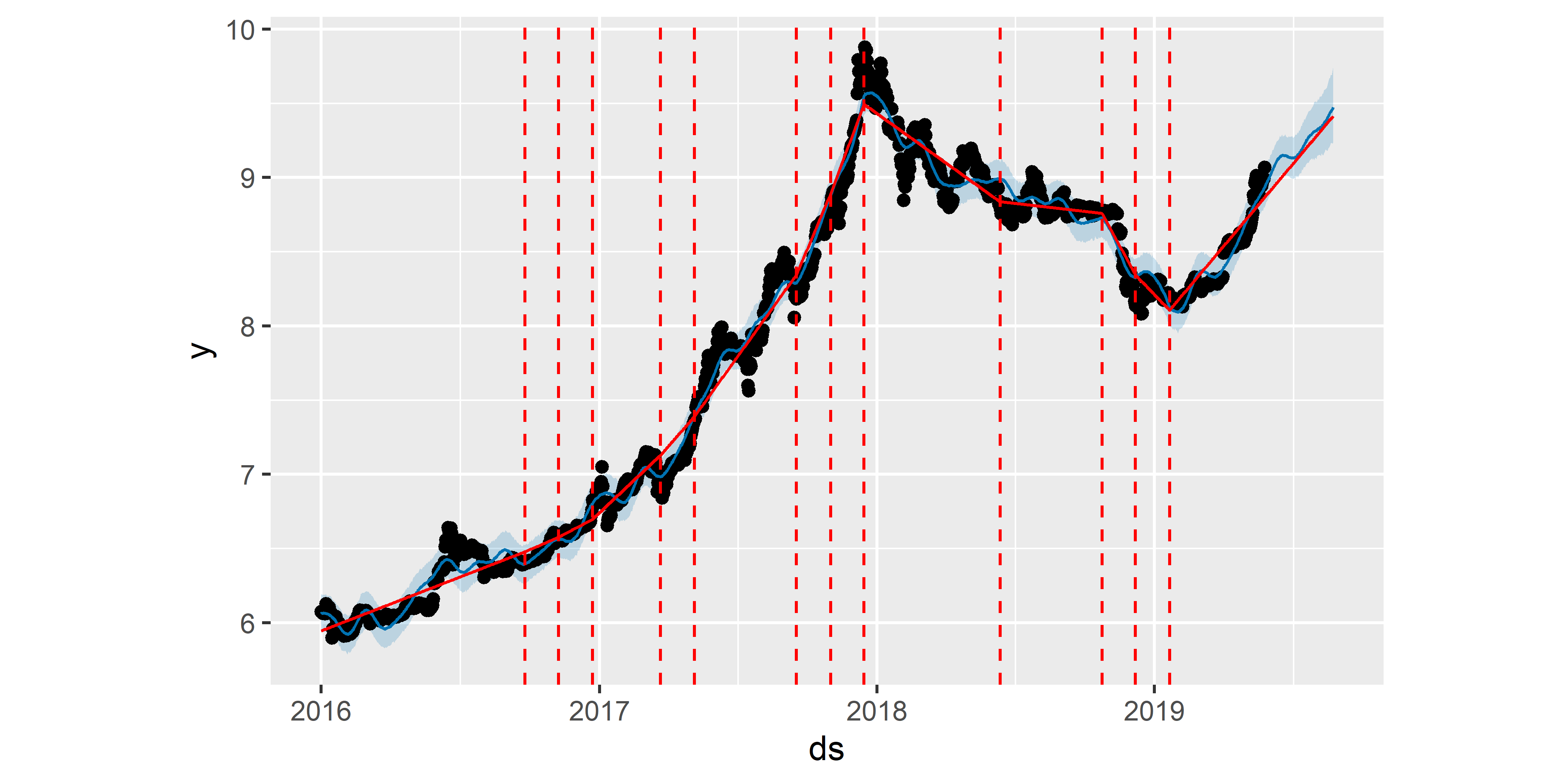
Как видно на рис. 6.6, полученная модель M2 намного лучше передает свойства анализируемого временного ряда. Это касается и получаемого с ее помощью прогноза (как с точки зрения направления тренда, так и с точки зрения ширины доверительных границ предсказанных значений).

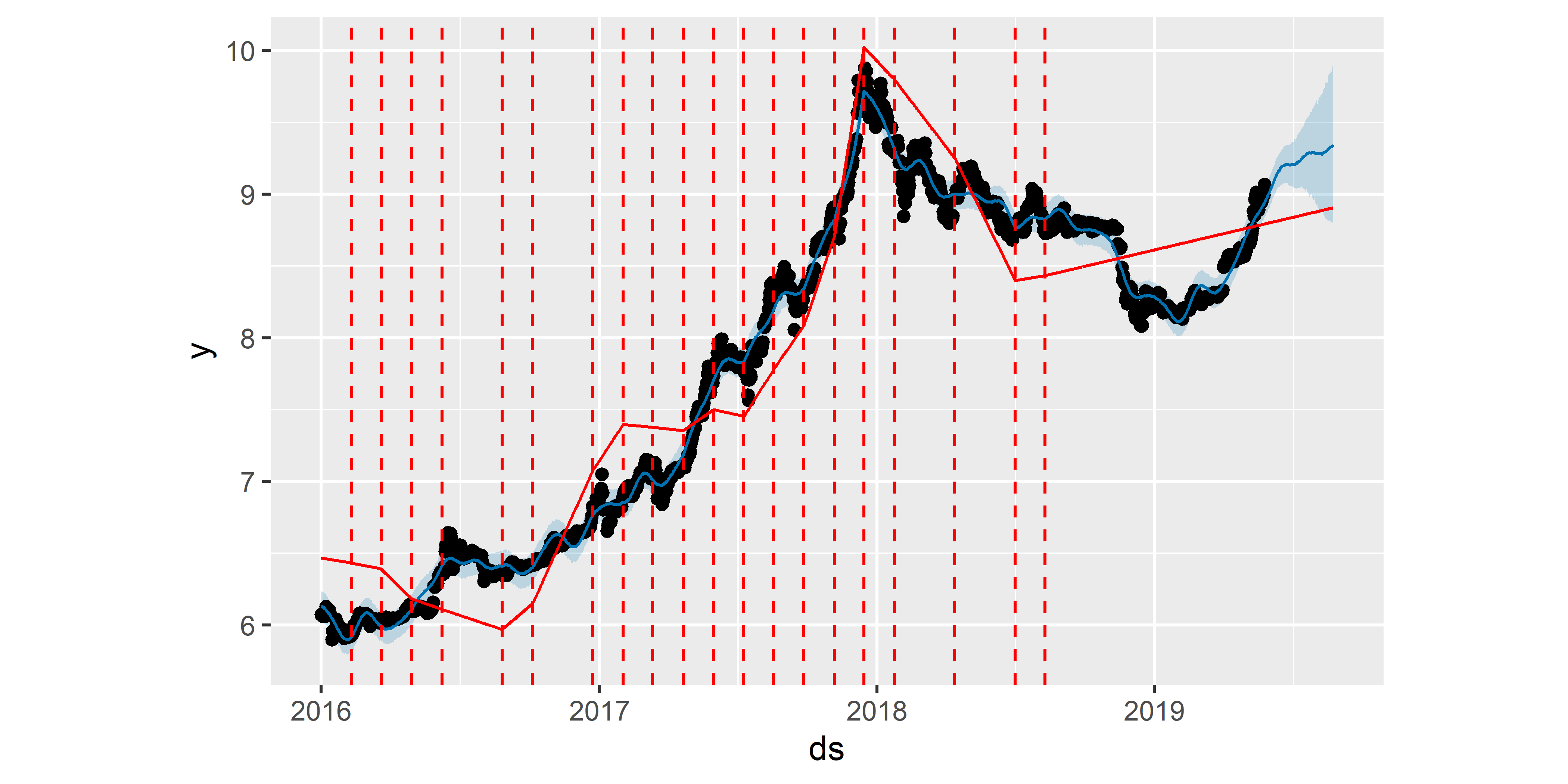
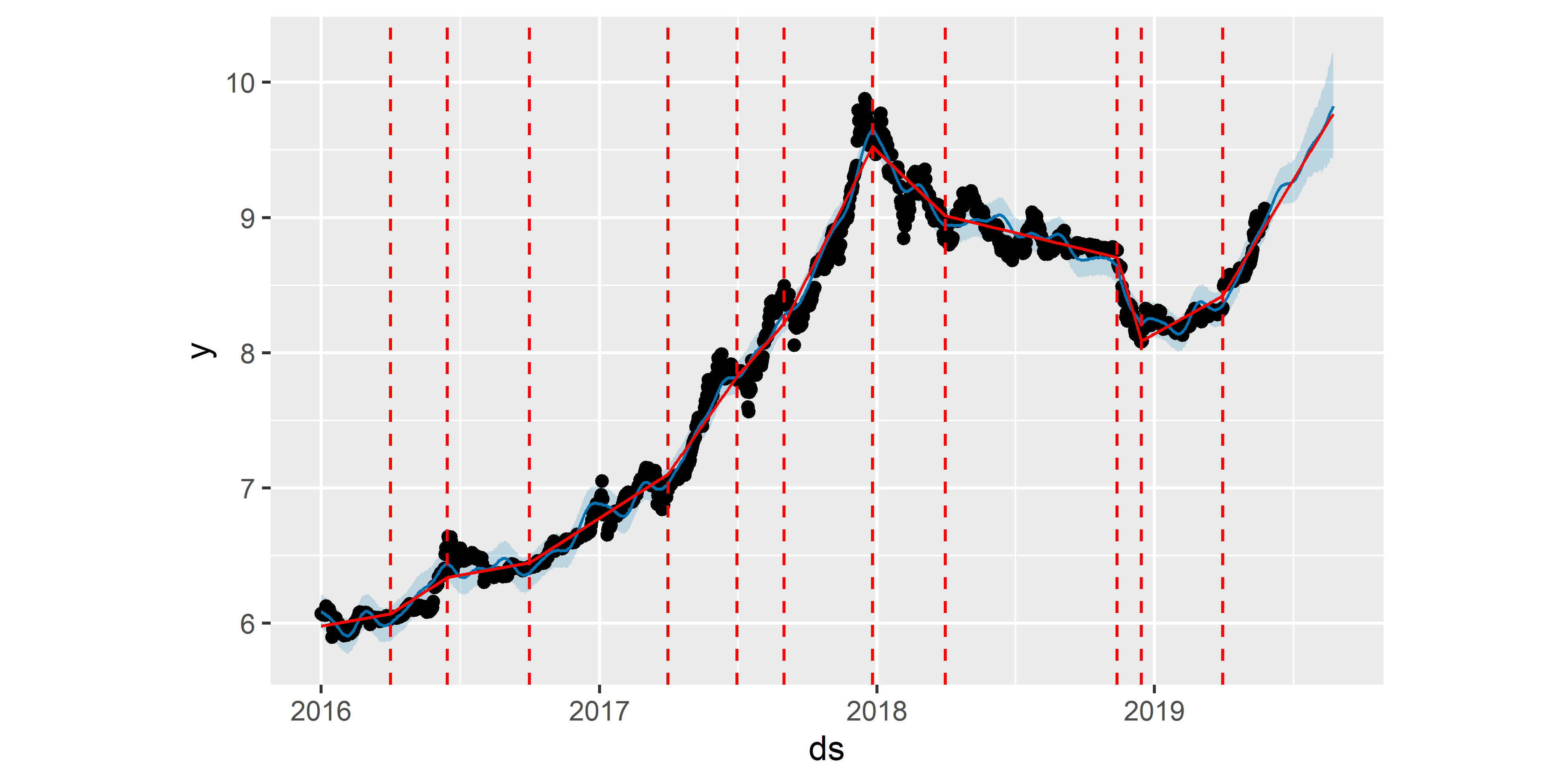
Наконец, посмотрим, что получится, если задать точки излома тренда “вручную”, а не оценивать их в автоматическом режиме. Для этого служит аргумент changepoints (рис. 6.8):

Модель M4 хорошо описывает тренд в анализируемом временном ряду, хотя не исключено, что она несколько переобучена.

6.5 Эффекты праздников и других важных событий

6.5.1 Формат представления

Как было отмечено в разд. 6.3, для добавления эффектов праздников в prophet –модель необходимо сначала создать отдельную таблицу, содержащую как минимум два обязательных столбца: holiday (названия праздников и других событий) и ds (временные метки; обычно это даты в формате YYYY-MM-DD ). Важно, чтобы в такую таблицу входил как исторический период, на основе которого происходит обучение модели, так и период в будущем, для которого необходимо сделать прогноз. Например, если какое–то важное событие встречается в обучающих данных, то его следует указать и для прогнозного периода (при условии, конечно, что мы ожидаем повторение этого события в будущем, и что дата этого события входит в прогнозный период).

История биткоина полна событий, которые косвенно или непосредственно оказали влияние на стоимость этой криптовалюты (см. также [здесь](https://en.wikipedia.org/wiki/History_of_bitcoin)). В качестве примера, возьмем некоторые из этих событий:

Теперь добавим эти события в модель (аргумент holidays ):

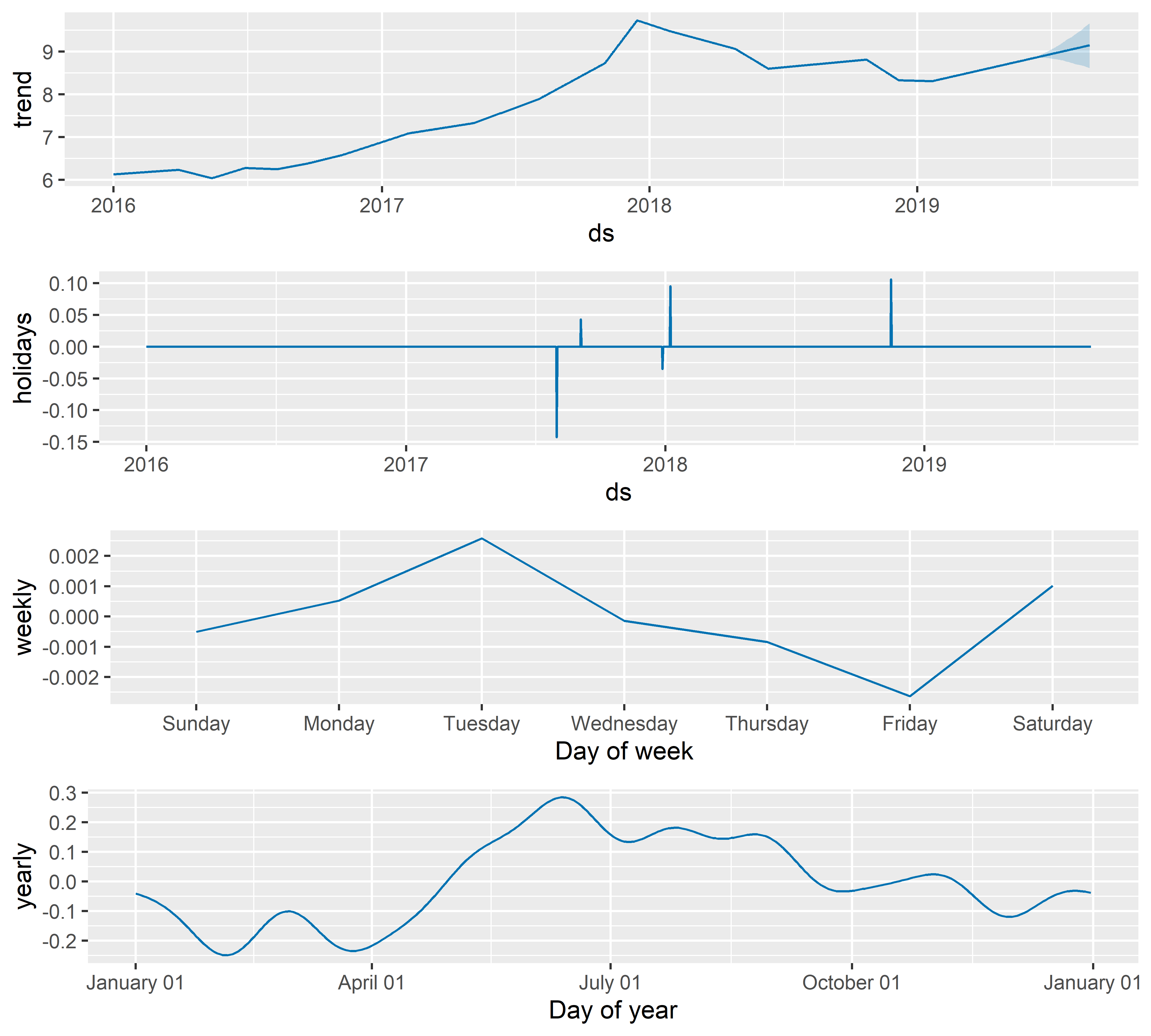
РИСУНОК 6.9: Оцененные компоненты модели M5

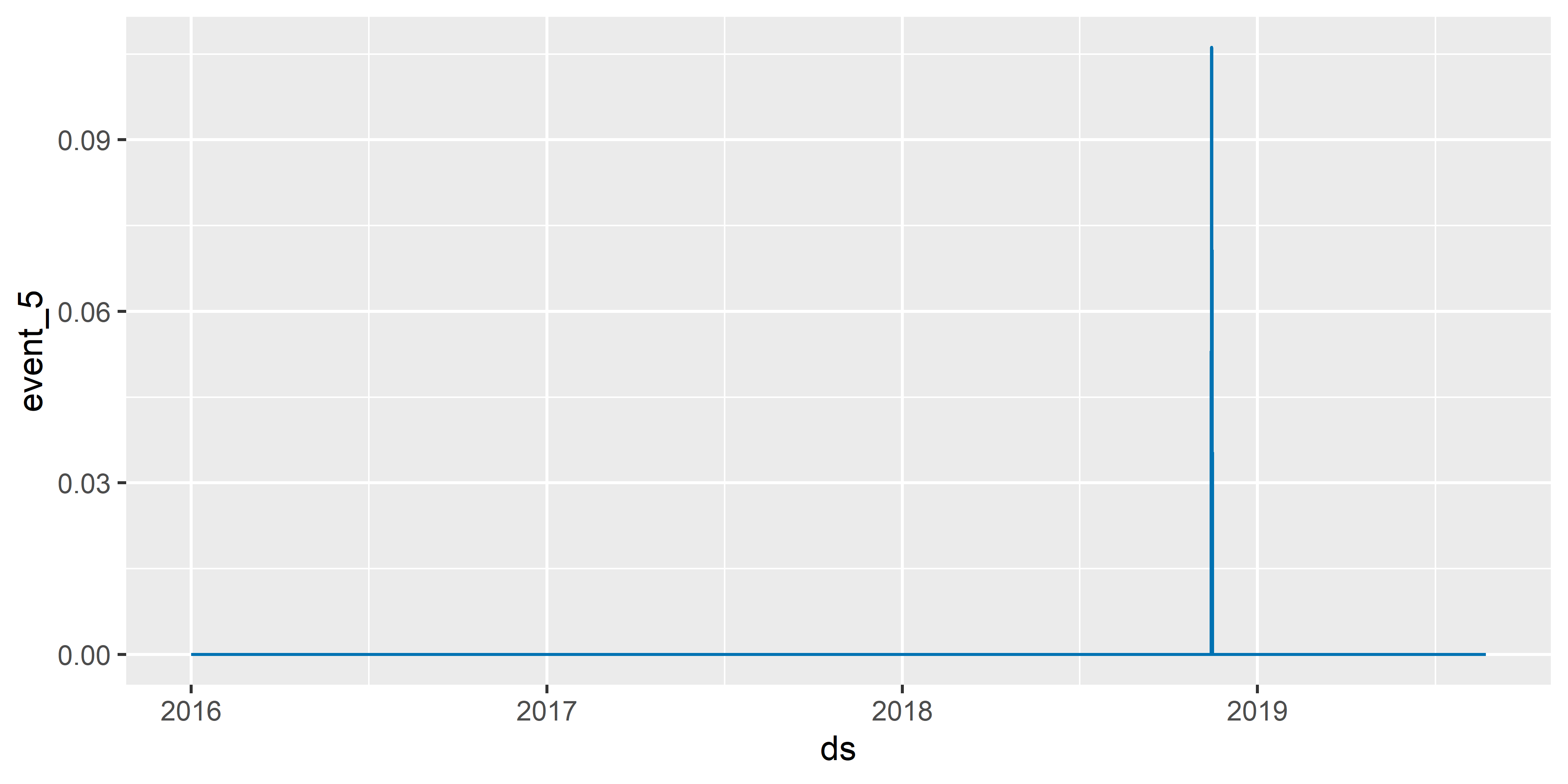
РИСУНОК 6.10: Эффект разветвления Bitcoin Cash на Bitcoin Cash SV и Bitcoing Cash ABC ( event_5 ), оцененный с помощью модели M5

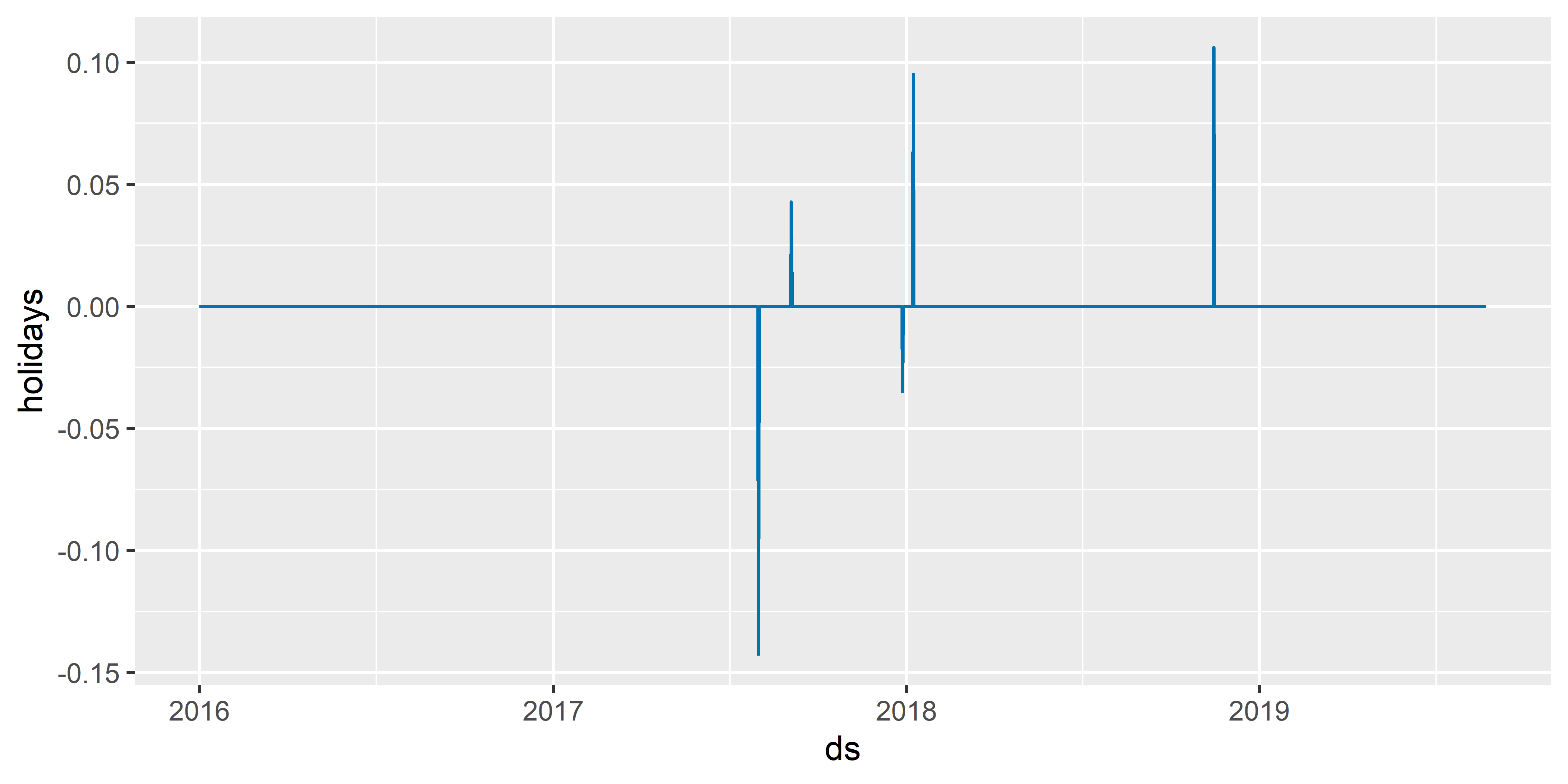
РИСУНОК 6.11: Эффекты всех событий, включенных в модель M5

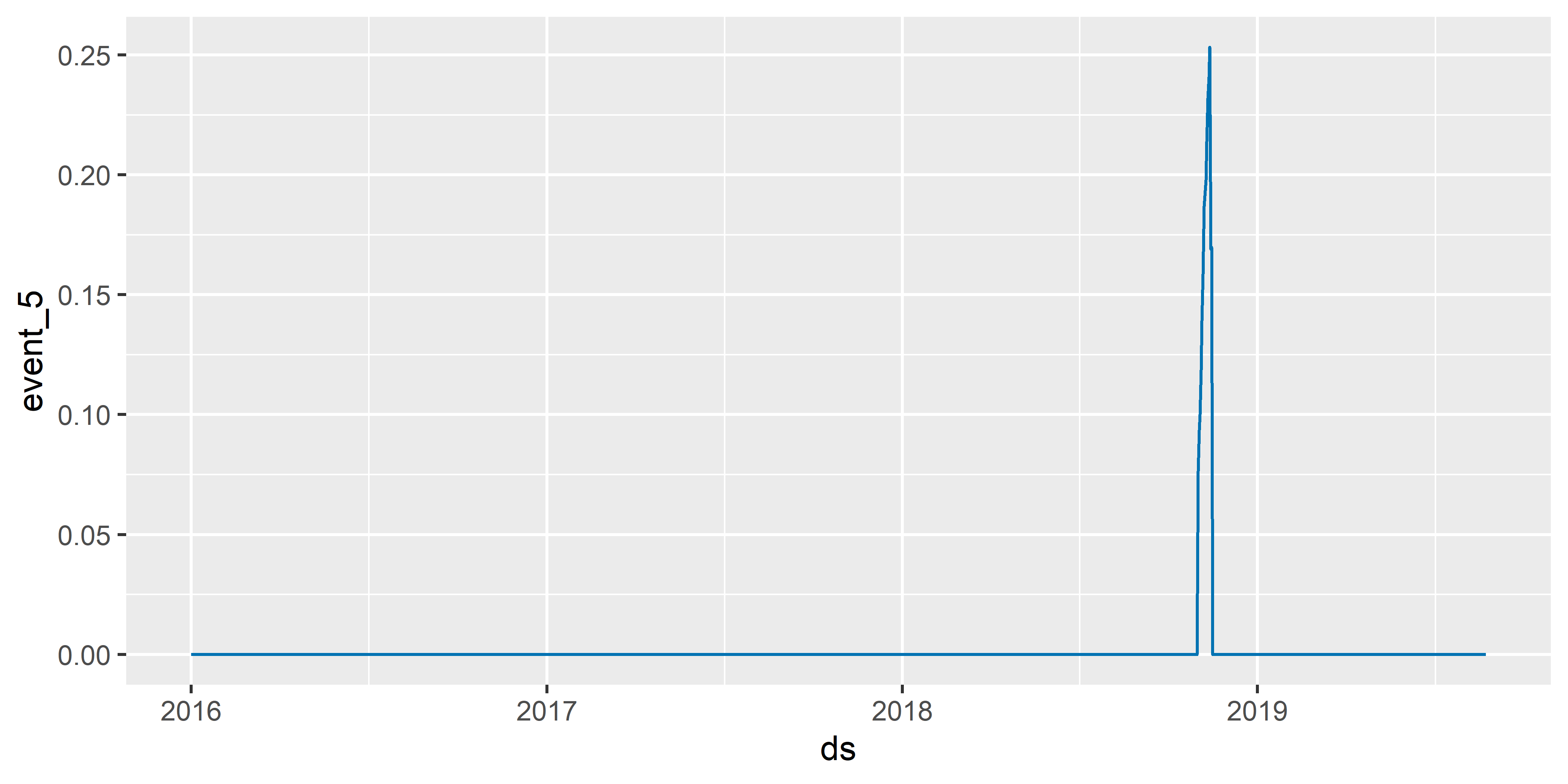
РИСУНОК 6.12: Эффект события с предысторией

Как видно на рис. 6.12, теперь эффект event_5 включает несколько дней до главной даты этого события (сравните с рис. 6.10).

6.5.2 Встроенные даты праздников

До этого момента мы моделировали эффекты событий, которые случались только один раз. Однако многие события, такие как официальные государственные праздники и выходные дни, повторяются регулярно и их эффекты также могут оказаться важными для прогноза.

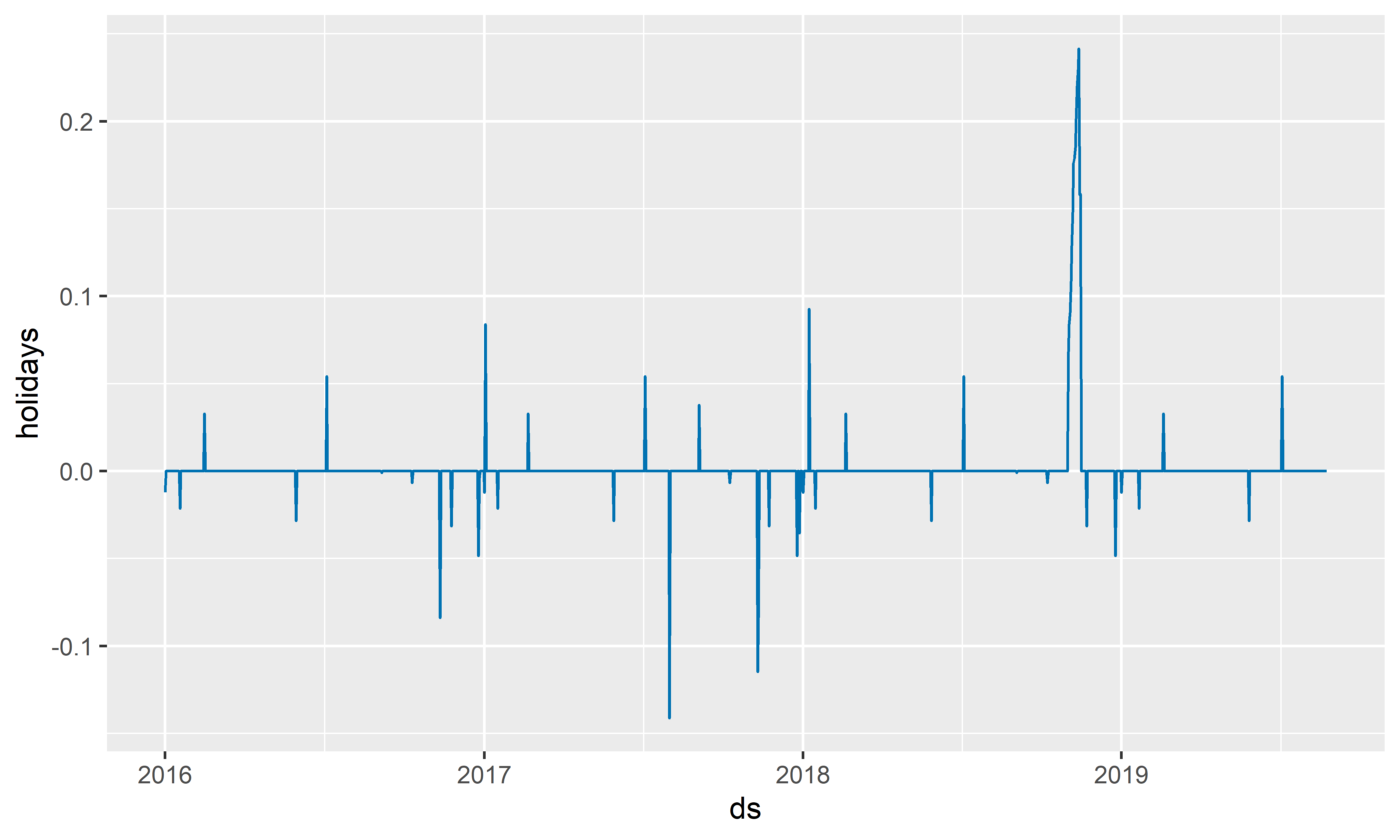
РИСУНОК 6.13: Эффекты разовых событий и официальных праздников США, оцененные с помощью модели M7

Оцененные эффекты всех событий из модели M7 показаны на рис. 6.13. Просмотреть названия этих событий можно следующим образом:

6.5.3 Регуляризация

В пакете prophet имеется возможность подавлять величину эффектов “праздников”, что может оказаться полезным при возникновении риска переобучения модели. Такой контроль (регуляризация) осуществляется одним из двух способов:

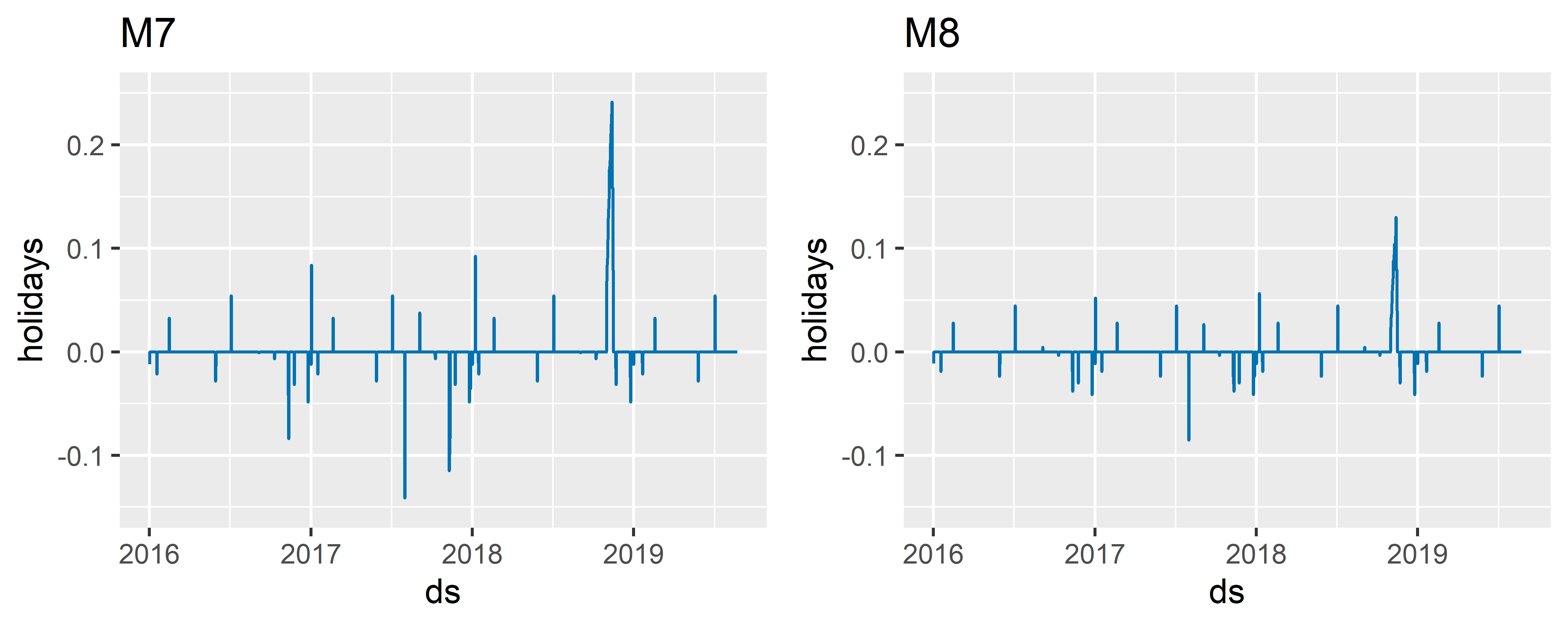
РИСУНОК 6.14: Эффекты событий до (модель M7 ) и после (модель M8 ) глобальной регуляризации

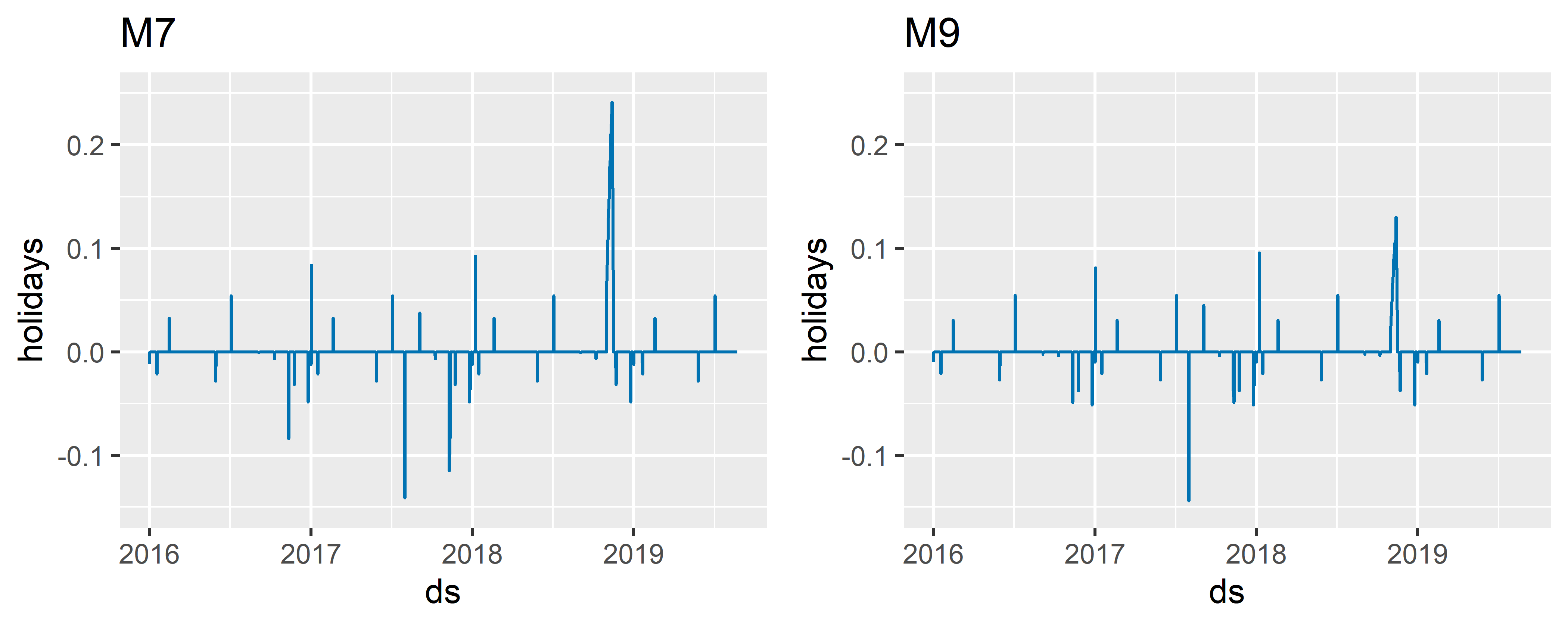
РИСУНОК 6.15: Пример регуляризации эффекта отдельного события

На рис. 6.15 хорошо виден результат подавления эффекта события event_5 (сравните уровень самого большого пика на графике слева с уровнем пика в той же позиции на графике справа). При этом эффекты большинства других событий и официальных праздников остались почти неизменными.

6.6 Сезонные компоненты

Как было отмечено в разд. 6.1, сезонные компоненты аппроксимируются в prophet с помощью частичных сумм ряда Фурье, число членов которого (порядок) определяет гладкость соответствующей функции. Рассмотрим различные способы спецификации сезонных колебаний.

6.6.1 Годовая, недельная и дневная компоненты

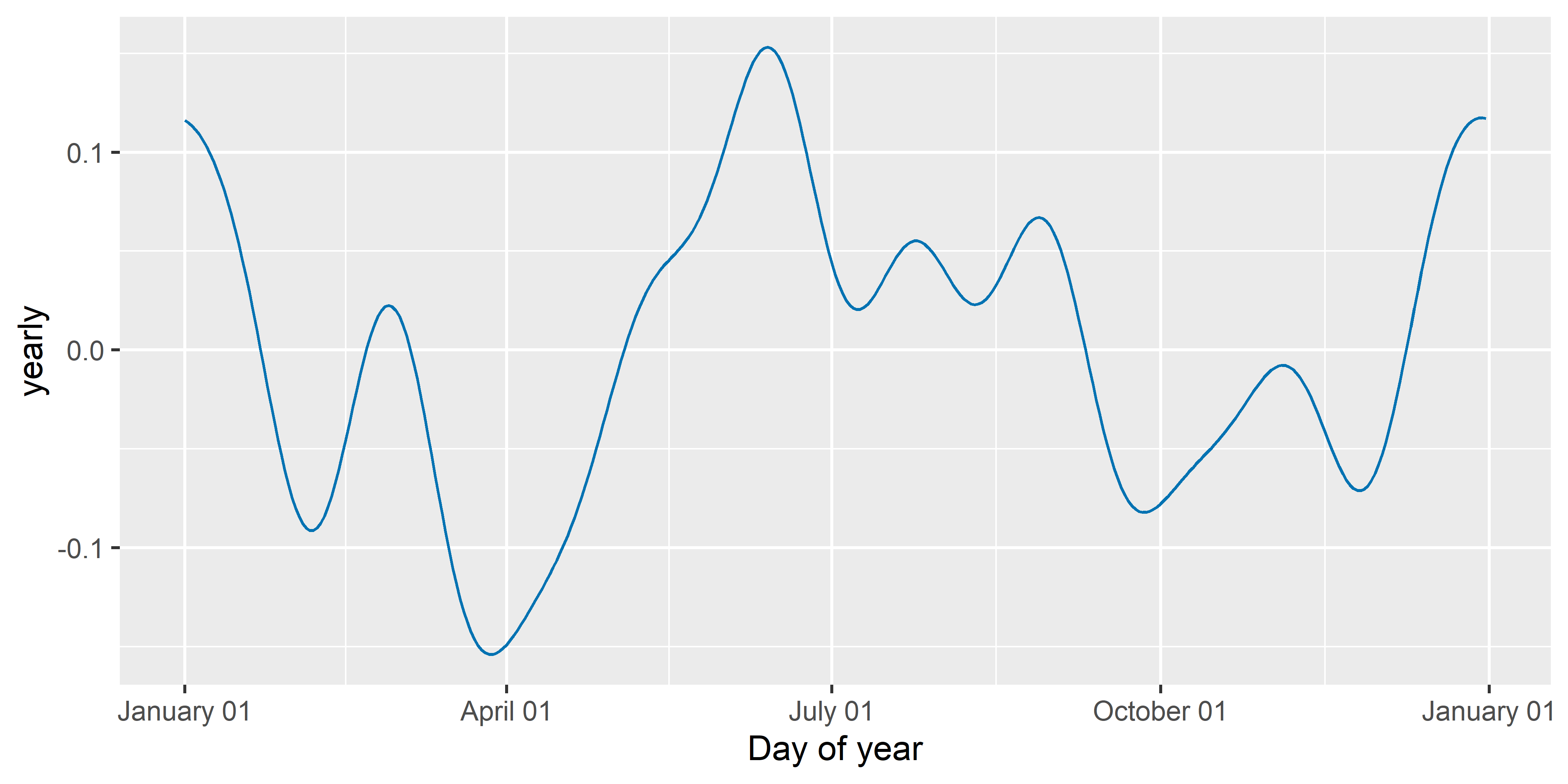
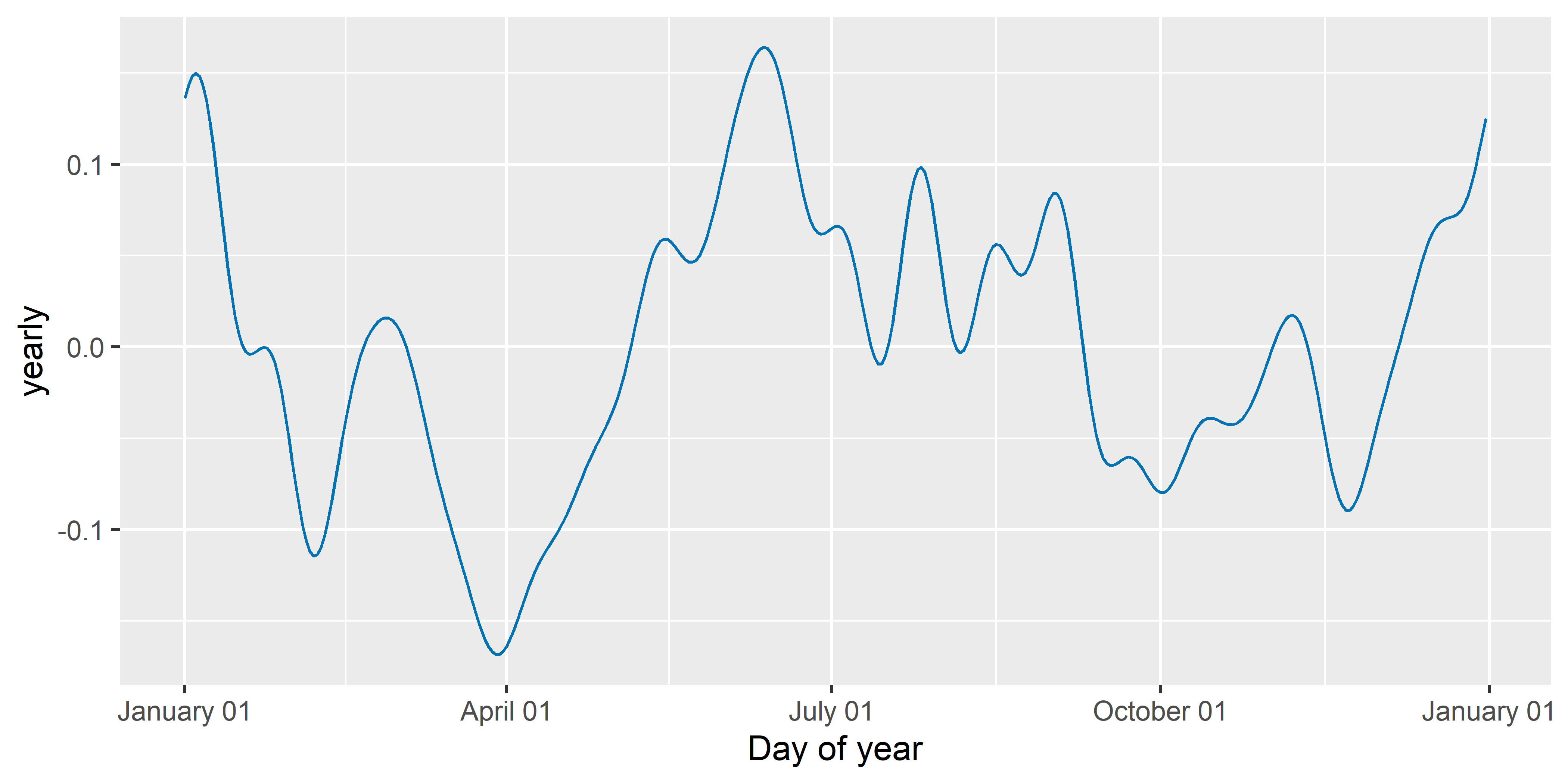
РИСУНОК 6.16: Функция годовой сезонности, оцененная с помощью модели M3

Увеличив значение аргумента yearly.seasonality с заданного по умолчанию 10 до 20, мы получим менее гладкую кривую (рис. 6.17):

РИСУНОК 6.17: Функция годовой сезонности, оцененная с помощью модели M3B

6.6.2 Пользовательские сезонные компоненты

Для данных, охватывающих как минимум два года, функция prophet() автоматически добавит в модель компоненты годовой и недельной сезонности. Если гранулярность данных превышает дневную (например, когда имеются почасовые наблюдения зависимой переменной), то в модель автоматически будет добавлена также и компонента дневной сезонности. Помимо этого, пользователи имеют возможность добавить и любые другие сезонные компоненты с помощью функции add_seasonality() (например, часовую, месячную, квартальную и т.п.). Эта функция имеет следующие аргументы:

Рассмотрим примеры использования функции add_seasonality() и ее аргументов.

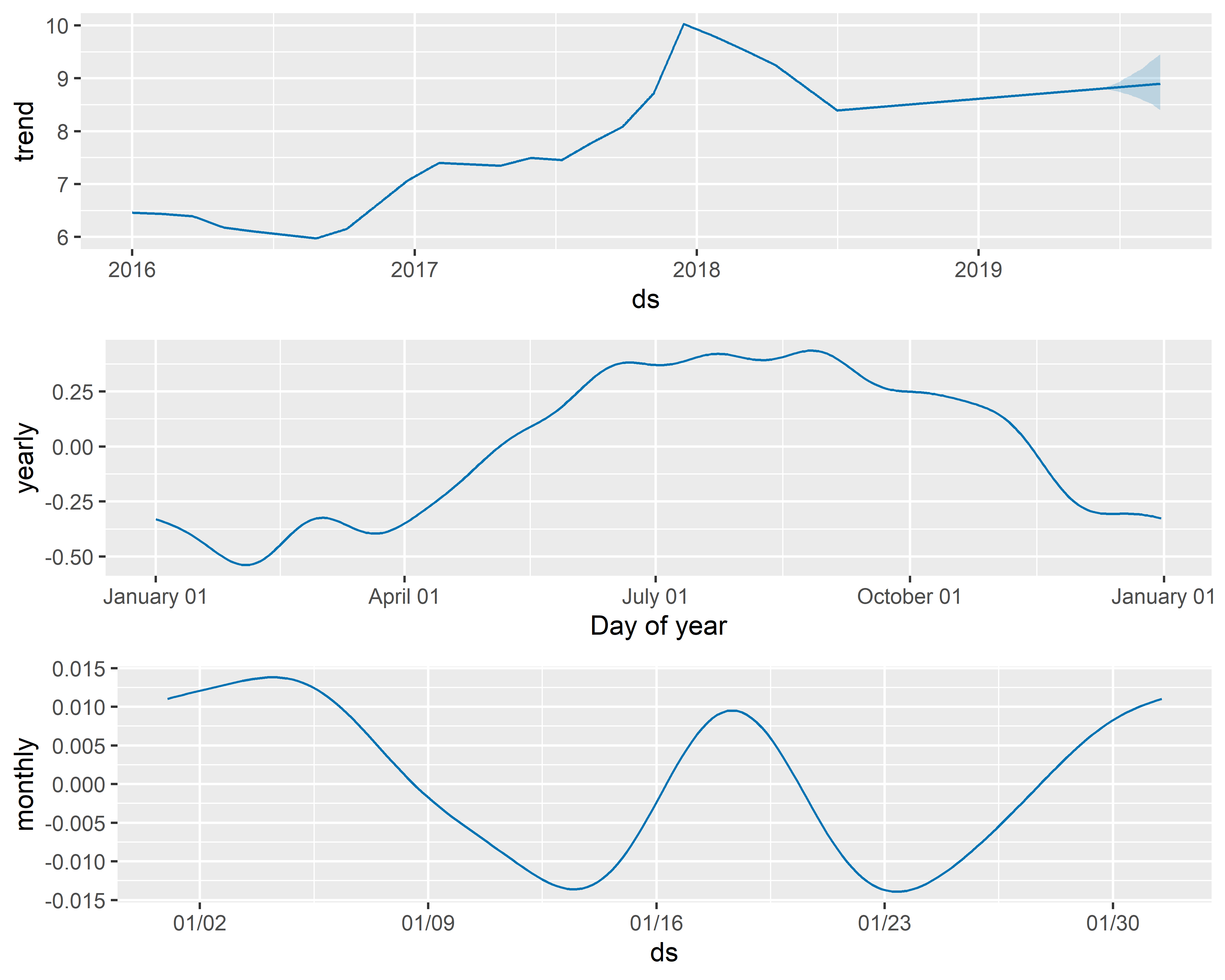
В приведенном ниже коде мы сначала отключаем автоматически добавляемую в модель недельную сезонность и вместо нее добавляем месячную (допустив, что один месячный период составляет 30.5 дней). На рис. 6.18 представлены все сезонные компоненты полученной модели (тренд, годовая сезонность и месячная сезонность).

РИСУНОК 6.18: Компоненты модели M10

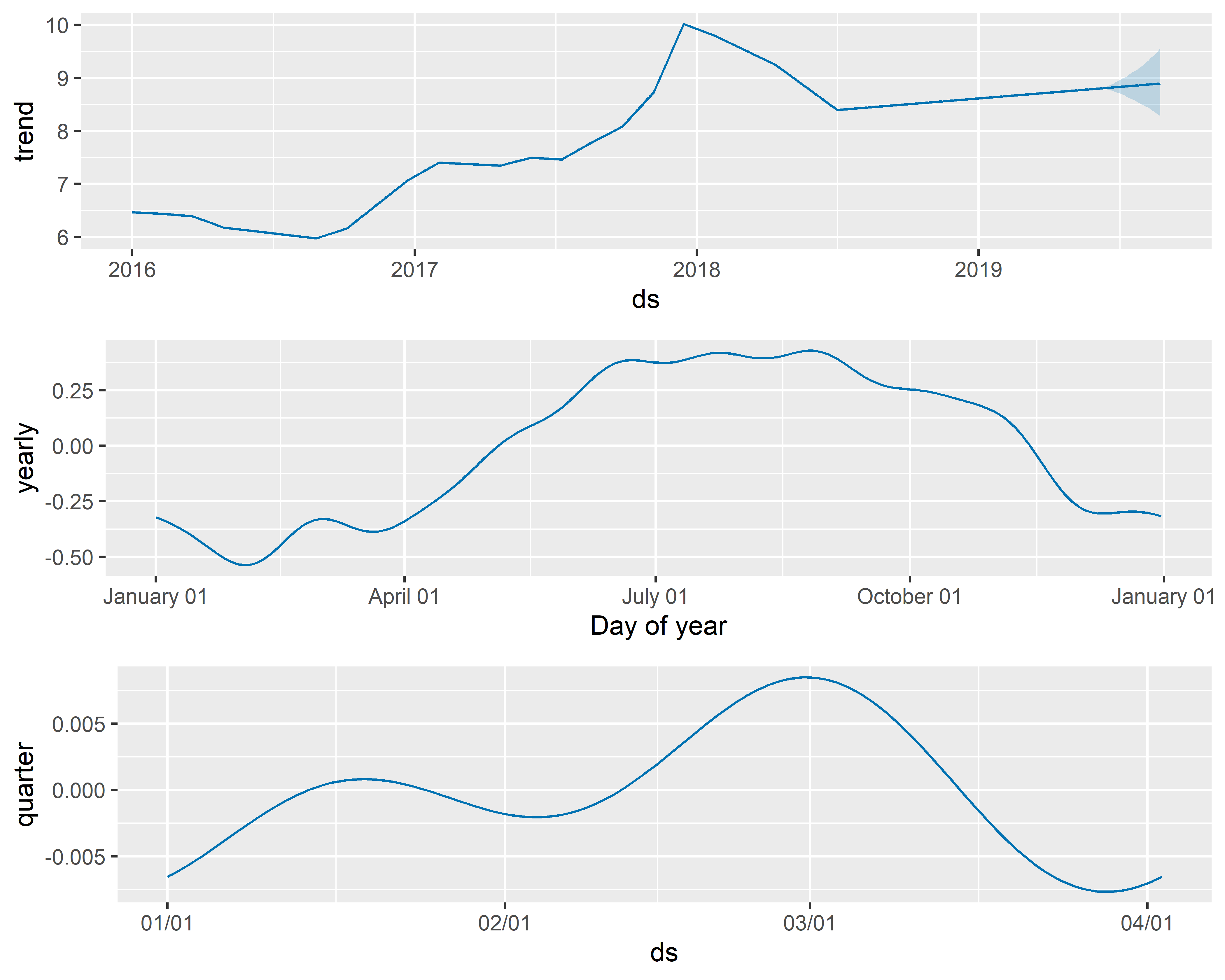
Аналогичным образом вместо компоненты месячных колебаний мы могли бы добавить, например, компоненту квартальной сезонности (задав период длиной 365.25/4 дней):

РИСУНОК 6.19: Компоненты модели M11

6.6.3 Условные режимы сезонности

Исключительно в качестве примера предположим, что недельные колебания стоимости биткоина в летние месяцы отличаются от таковых в другие месяцы. Чтобы смоделировать такое различие добавим в таблицу с данными bitcoin_train две новые индикаторные переменные: summer (принимает значение TRUE в летние месяцы и FALSE в другие месяцы) и not_summer ( TRUE в нелетние месяцы и FALSE летом). Важно помнить, что такие же переменные нужно добавить и в таблицу с будущими датами future_df — иначе прогнозные значения рассчитать не получится:

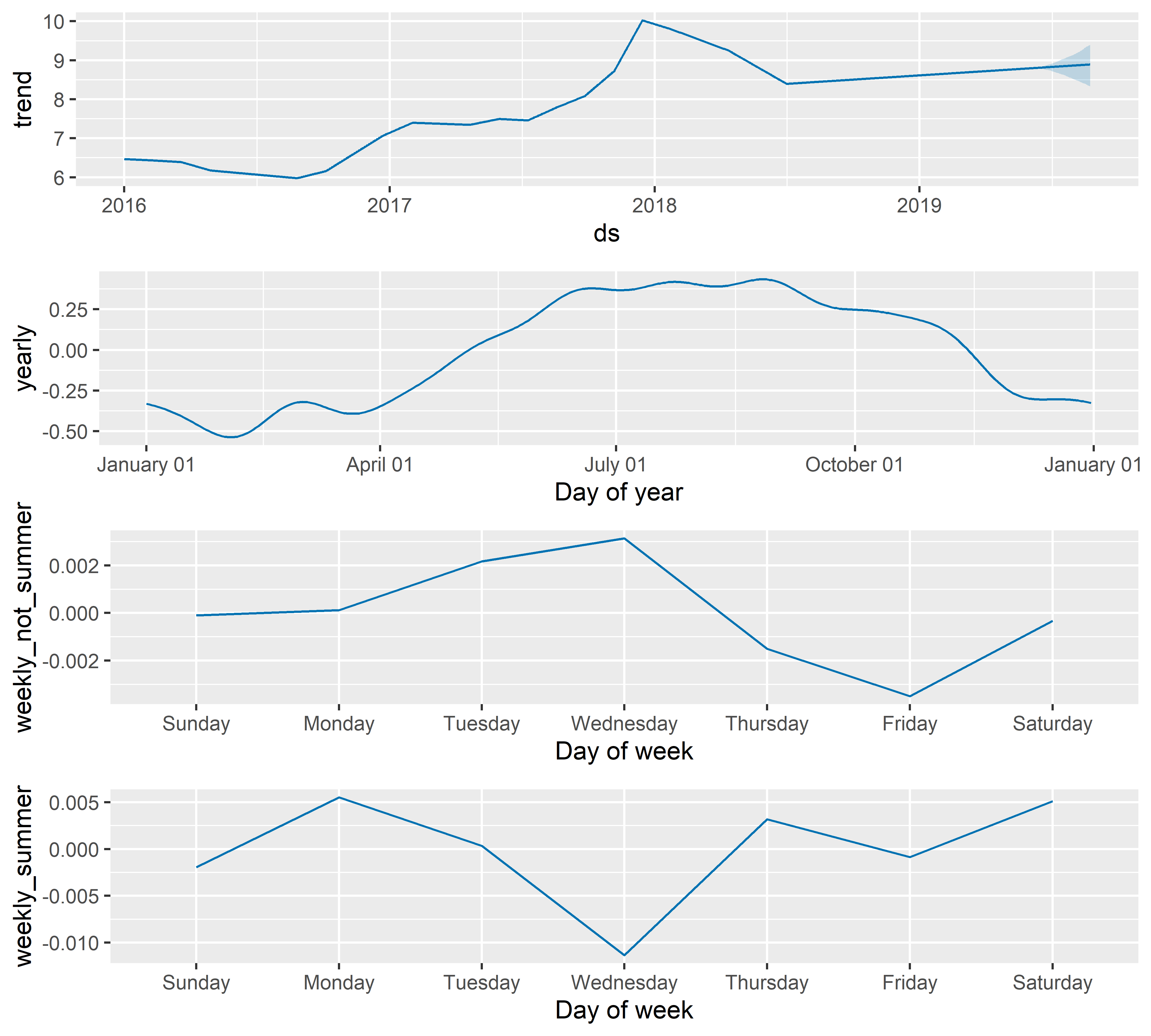
РИСУНОК 6.20: Оцененные компоненты модели M12

Согласно полученной модели, в нелетние месяцы стоимость биткоина в течение недели обычно достигает максимума по средам, тогда как в летние месяцы по средам обычно наблюдается противоположная картина (рис. 6.20).

6.6.4 Регуляризация сезонных компонент

6.6.5 Аддитивная и мультипликативная сезонности

Как было отмечено в разд. 1.3, по характеру функциональной связи между своими компонентами модели временных рядов делятся на два основных типа — аддитивные и мультипликативные. Первый из них применяется в случаях, когда амплитуда сезонных колебаний приблизительно постоянна. Если же эта амплитуда заметно изменяется во времени (обычно возрастает), то строят мультипликативную модель.

В пакете prophet по умолчанию подгоняются аддитивные модели временных рядов (разд. 6.1). В мультипликативных моделях, как следует из их названия, сезонная компонента умножается на тренд (в связи с этим вклад сезонных колебаний моделируется в виде доли (%) от уровня тренда):

\[y(t) = g(t) \times s(t) + h(t) + \epsilon_t.\]

В приведенном уравнении предполагается, что амплитуда всех сезонных компонент существенно изменяется во времени. Для подгонки соответствующих моделей необходимо воспользоваться аргументом seasonality.mode функции prophet() (рис. 6.21):

РИСУНОК 6.21: Прогноз стоимости биткоина, полученный на основе модели M14

Однако в пакете prophet имеется возможность и более тонкого контроля над аддитивностью сезонных компонент. Так, например, можно построить модели, в которых недельная колебания представлены в аддитивном виде, а годовые — в мультипликативном. Вероятно, вы уже догадались, что для этого применяется функция add_seasonality() :

РИСУНОК 6.22: Оцененные компоненты модели M15

6.7 Модели с предикторами

Добавим в модель стоимости биткоина три предиктора: цены на акции компаний Amazon, Google и Facebook, хранящиеся в таблице shares_na_filled (гл. 2). Нужно подчеркнуть, что выбор цен на акции в качестве предикторов, равно как и выбор именно этих компаний, ни с чем не связаны — просто такие данные легко получить из публично доступных источников. Добавим эти данные в таблицу bitcoin_train :

Обратите внимание: даты в обеих объединенных нами таблицах лежат в пределах от 2016-01-01 до 2019-05-26 (включительно), что соответствует периоду обучающих данных. Важно также понимать, что на момент написания этого раздела (октябрь 2019 г.) интересующий нас прогнозный период (c 2019-05-27 по 2019-08-24 ) уже стал историей и, соответственно, цены на акции для этого периода были известны. Но, конечно же, мы не можем использовать эти ставшие историей данные для прогнозирования стоимости биткоина на период с 2019-05-27 по 2019-08-24 : в реальной ситуации при расчете прогноза подобное “заглядывание в будущее” было бы невозможно.

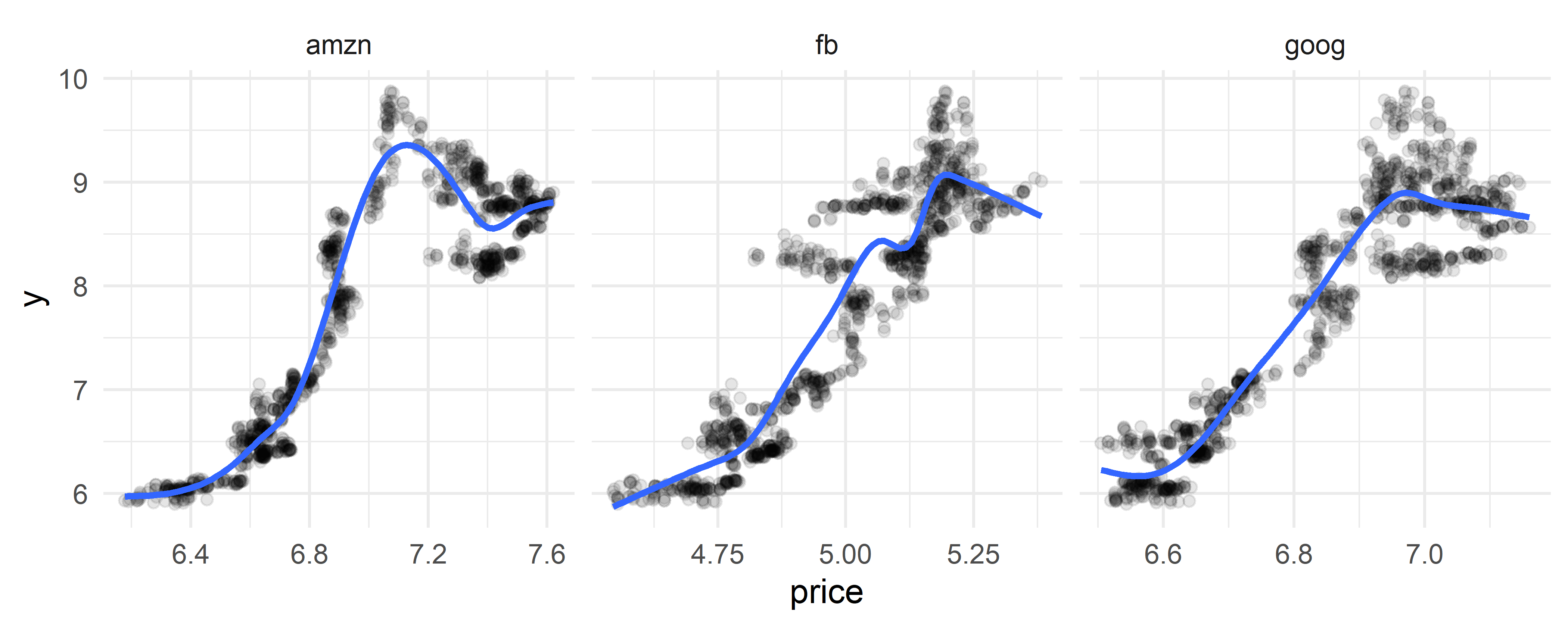
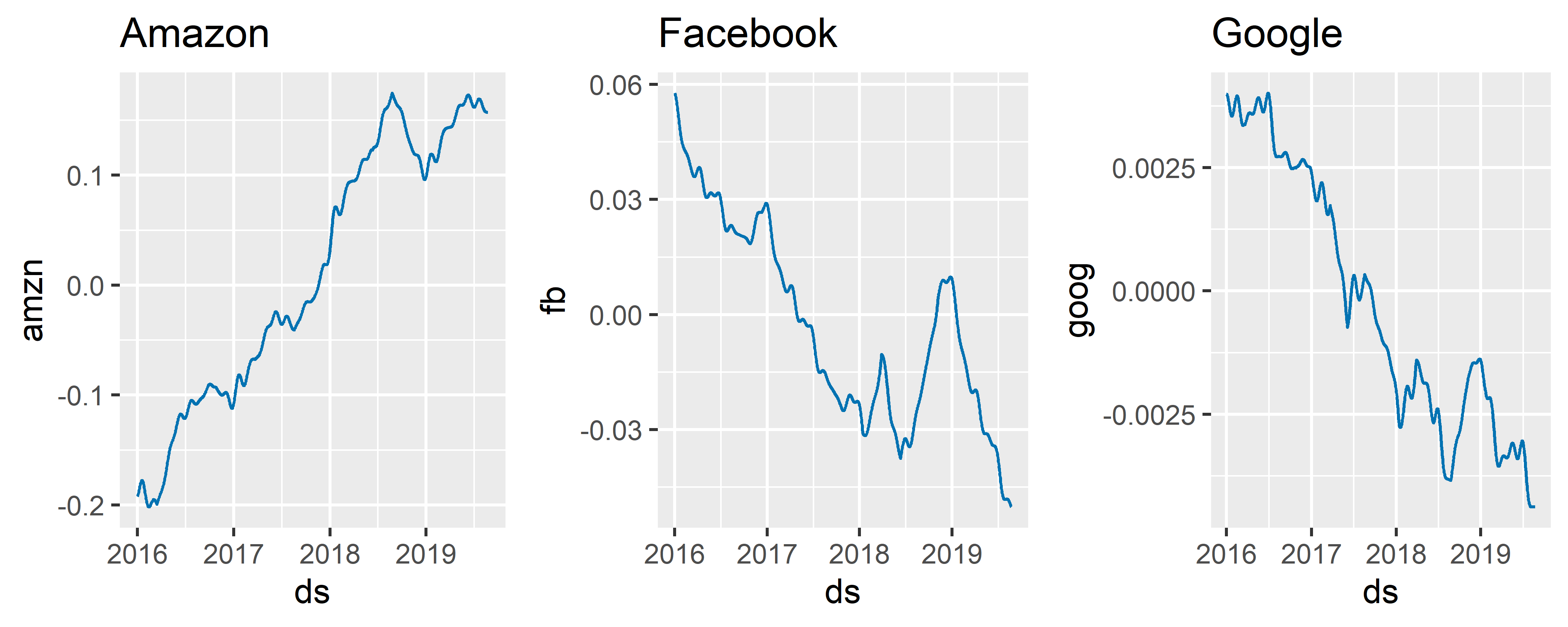
Как отмечено выше, цены на акции Amazon, Google и Facebook выбраны в качестве предикторов исключительно из удобства. Тем не менее, все три переменные демонстрируют определенную (нелинейную) связь со стоимостью биткоина и, соответственно, вполне подходят для наших целей (рис. 6.23):

РИСУНОК 6.23: Связь между ценой акций трех компаний и стоимостью биткоина

Однако прежде, чем перейти к построению модели стоимости биткоина, нам необходимо решить проблему с будущими значениями предикторов. Для этого мы построим отдельные модели для каждого предиктора, а затем рассчитаем их предсказанные значения для интересующего нас прогнозного периода:

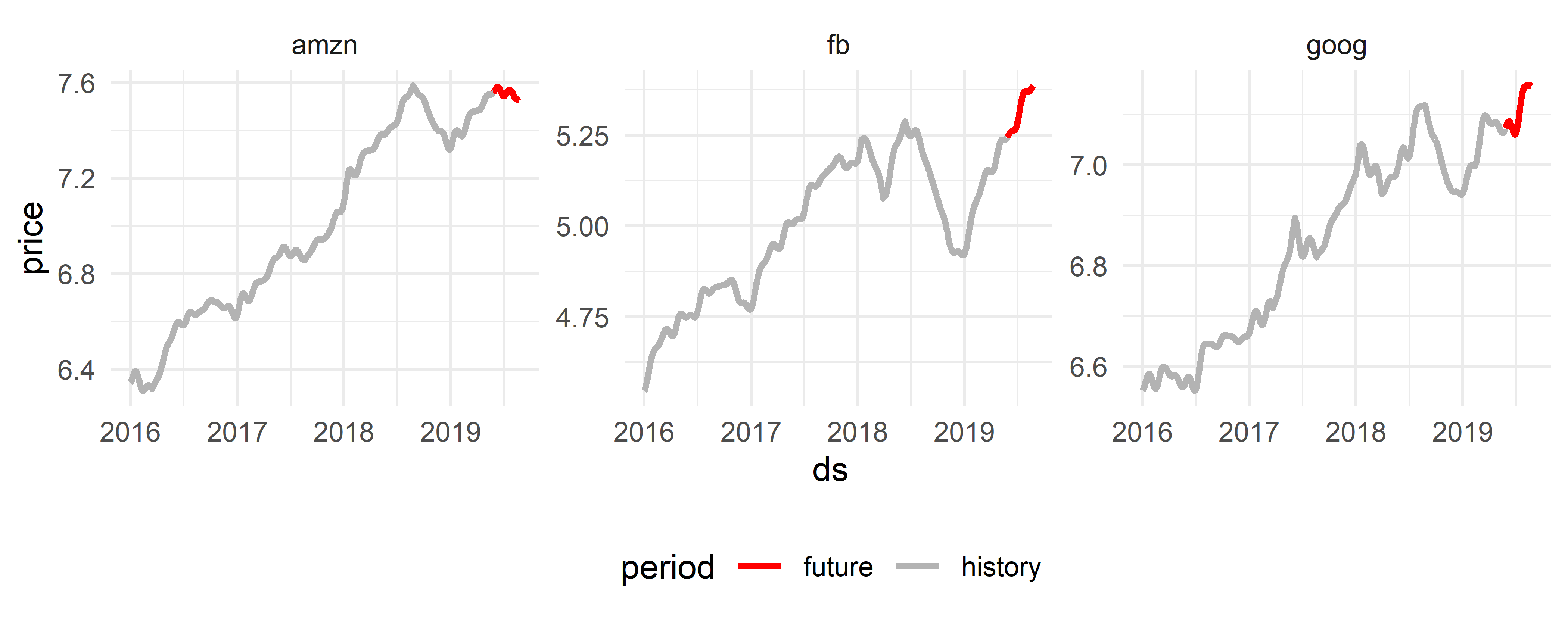
Исходные данные и прогнозные значения цен на акции показаны на рис. 6.24.

РИСУНОК 6.24: Исторические данные по цене акций (серые линии) и предсказанные значения (красные линии)

Теперь у нас есть все, чтобы построить модель стоимости биткоина с тремя предикторами и рассчитать прогнозные значения (рис. 6.25):

РИСУНОК 6.25: Прогноз стоимости биткоина, полученный на основе модели M16

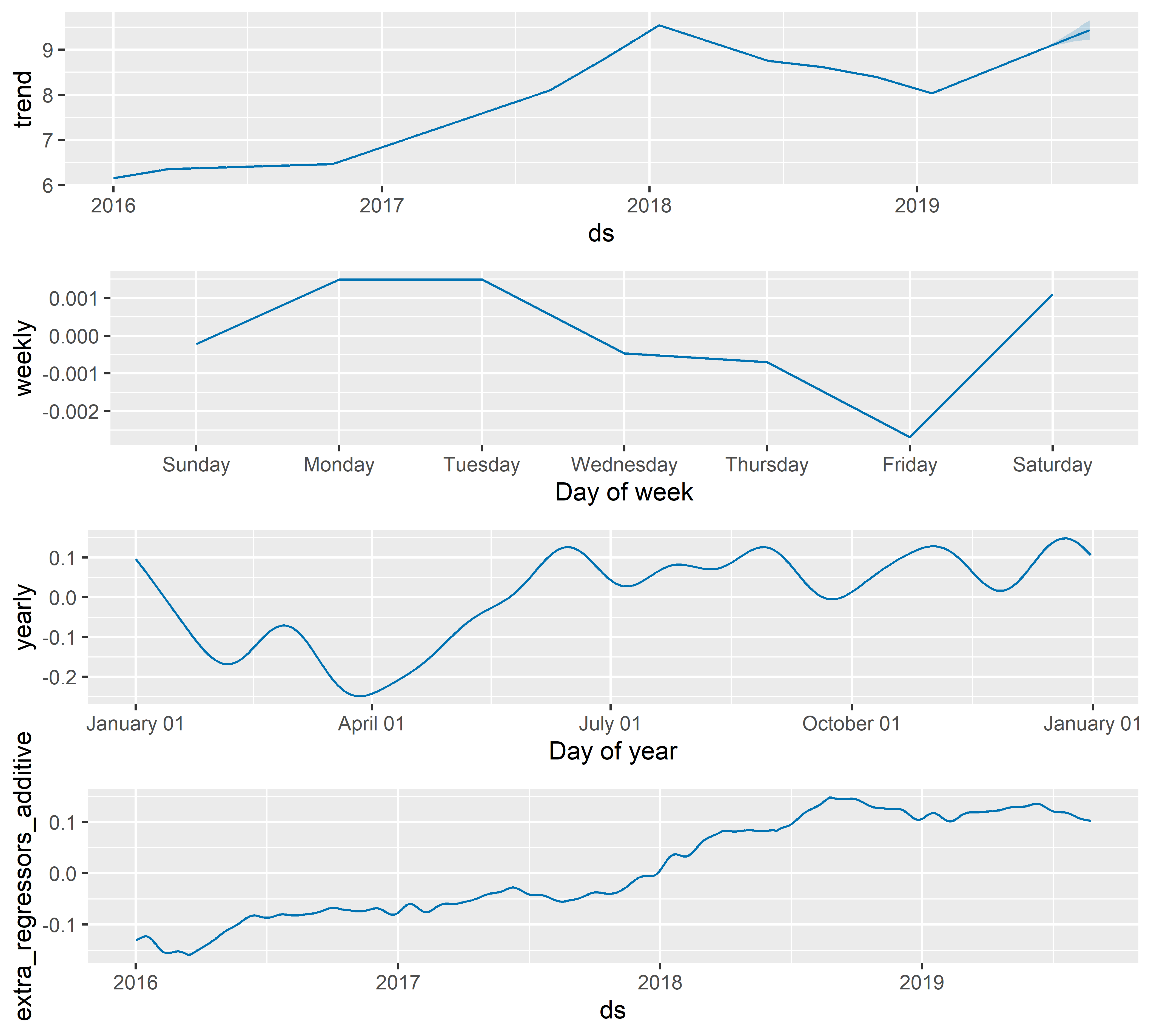
РИСУНОК 6.26: Оцененные компоненты модели M16

С помощью рассмотренной ранее функции plot_forecast_component() (разд. 6.5) мы можем также изобразить эффекты отдельных предикторов (рис. 6.27):

РИСУНОК 6.27: Оцененные эффекты предикторов, включенных в модель M16

6.8 Выбор оптимальной модели

К сожалению, в случае с моделями временных рядов такой способ выполнения перекрестной проверки не имеет смысла и не отвечает стоящей задаче. Поскольку во временных рядах, как правило, имеет место значительная автокорреляция (гл. 4), то мы не можем просто разбить такой ряд случайным образом на \(K\) частей — это приведет к потере указанной корреляции. Более того, в результате случайного разбиения данных на несколько блоков может получиться так, что в какой–то из итераций мы построим модель преимущественно по недавним наблюдениям, а затем оценим ее качество на блоке из давних наблюдений. Другими словами, мы построим модель, которая будет предсказывать прошлое, что не имеет никакого смысла — ведь мы пытаемся решить задачу по предсказанию будущего!

6.8.1 Метод имитированных исторических прогнозов

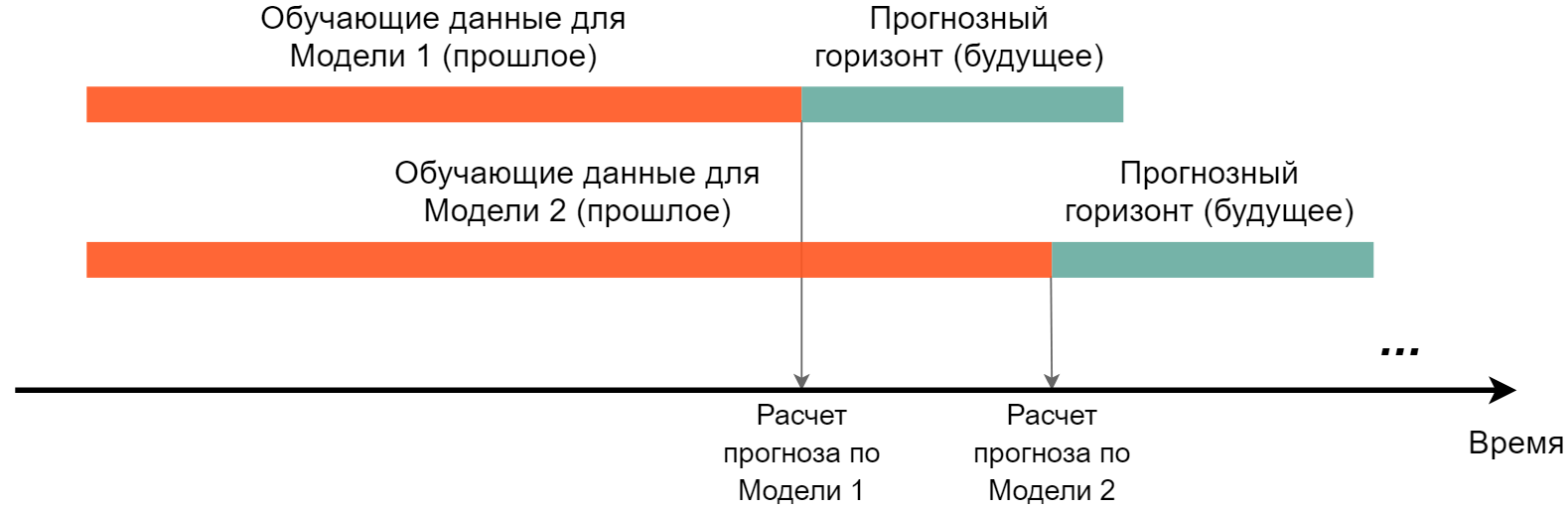
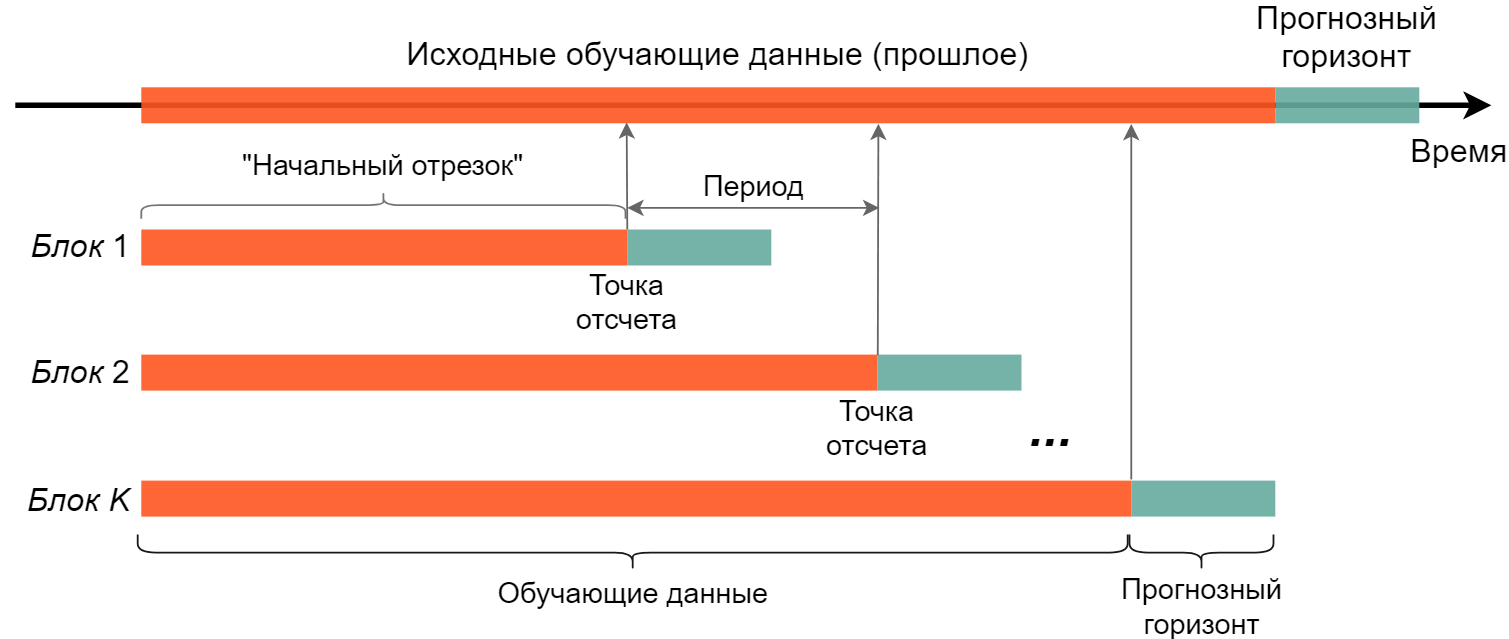
Любая модель временного ряда строится на основе данных, собранных в течение некоторого периода в прошлом. Далее по полученной модели рассчитываются прогнозные значения для интересующего нас промежутка времени (горизонта) в будущем. Такая процедура повторяется каждый раз, когда необходимо сделать новый прогноз (рис. 6.28).

РИСУНОК 6.28: Стандартная процедура построения моделей для прогнозирования временных рядов

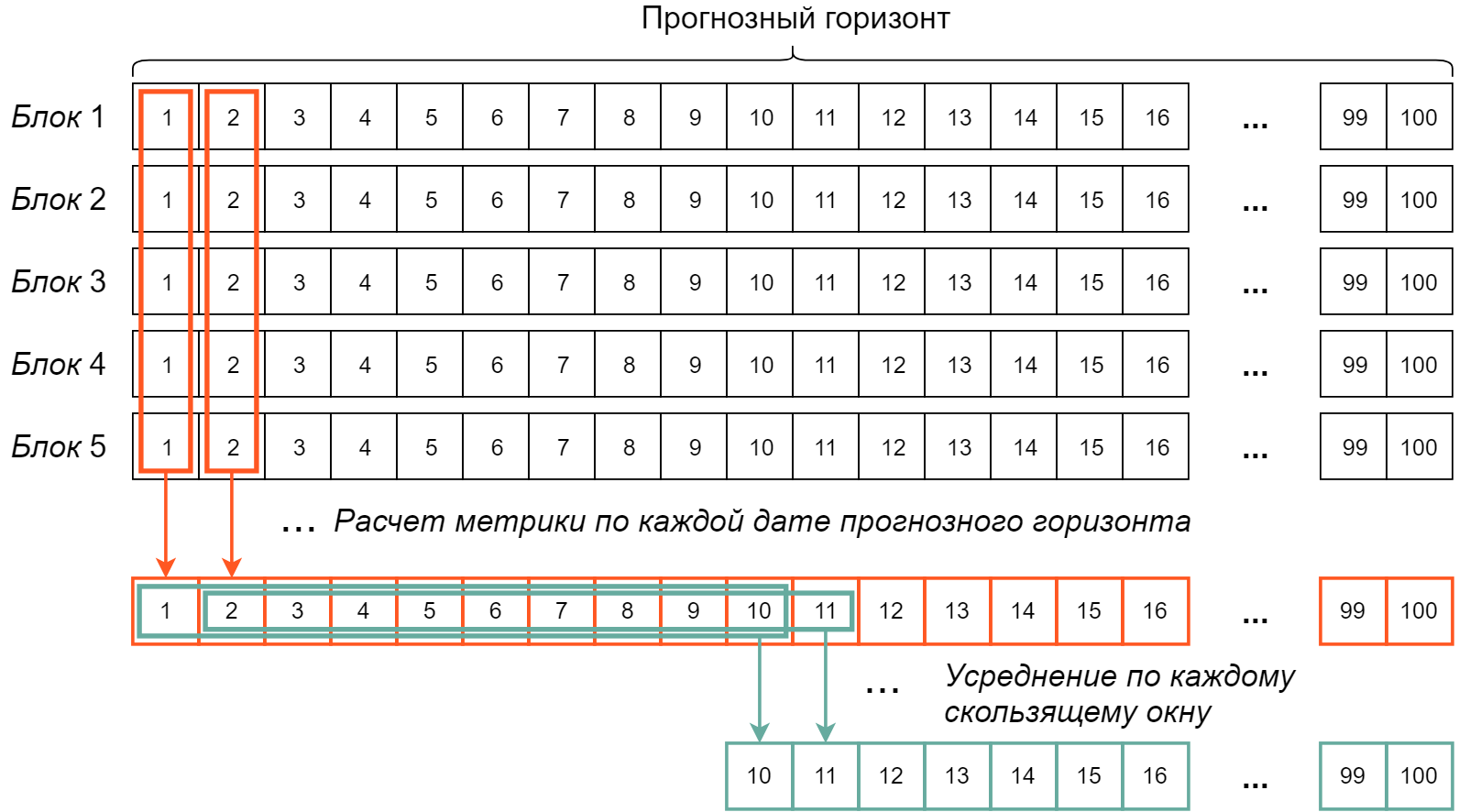
Каждый раз после подгонки модели на обучающих данных из \(k\) –го блока рассчитываются предсказания для прогнозного горизонта того же блока, что позволяет оценить качество прогноза с помощью подходящей случаю метрики (например, RMSE; см. ниже). Значения этой метрики, усредненные по каждой дате прогнозных горизонтов каждого блока, в итоге дают оценку качества предсказаний, которую можно ожидать от модели, построенной по всем исходным обучающим данным. Это в свою очередь позволяет сравнить несколько альтернативных моделей и выбрать оптимальную.

РИСУНОК 6.29: Процедура, лежащая в основе метода имитированных исторических прогнозов

6.8.2 Выполнение перекрестной проверки

Функция cross_validation() возвращает таблицу c наблюденными ( y ) и оцененными ( yhat ) значениями моделируемой переменной, а также доверительными границами предсказанных значений ( yhat_lower и yhat_upper ) для каждой точки отсчета cutoff и каждой даты ds соответствующего прогнозного периода (в примере используется модель M3 из разд. 6.4):

6.8.3 Метрики качества модели

Как следует из ее названия, функция performance_metrics() позволяет рассчитать метрики, характеризующие качество предсказаний моделей. В частности, имеется возможность рассчитать следующие показатели:

В приведенных формулах \(y_i\) и \(\hat_i\) — это истинное и предсказанное значения моделируемой переменной соответственно, а \(n\) — количество наблюдений.

Функция performance_metrics() имеет следующие аргументы:

РИСУНОК 6.30: Процедура расчета метрик качества моделей при выполнении перекрестной проверки по методу SHF

В приведенном ниже примере функция performance_metrics() применена для расчета среднеквадратичной ошибки прогноза построенной нами ранее модели M3 :

Как видно из полученного результата, первое усредненное значение MSE приходится на 9–й день прогнозного горизонта, поскольку длина этого горизонта для модели M3 составляет 90 дней (см. выше код для создания таблицы M3_cv ), а 9 — это 10% от этой длины (размер скользящего окна, задаваемый аргументом rolling_window ).

Если аргументу rolling_window присвоить значение 0, то запрашиваемые метрики качества будут рассчитаны для каждой даты прогнозного горизонта (т.е. размер скользящего окна в данном случае фактически равен 1):

Если же аргументу rolling_window присвоить значение 1, то запрашиваемые метрики качества будут усреднены по всему прогнозному горизонту:

Функция plot_cross_validation_metric() возвращает объект класса ggplot :

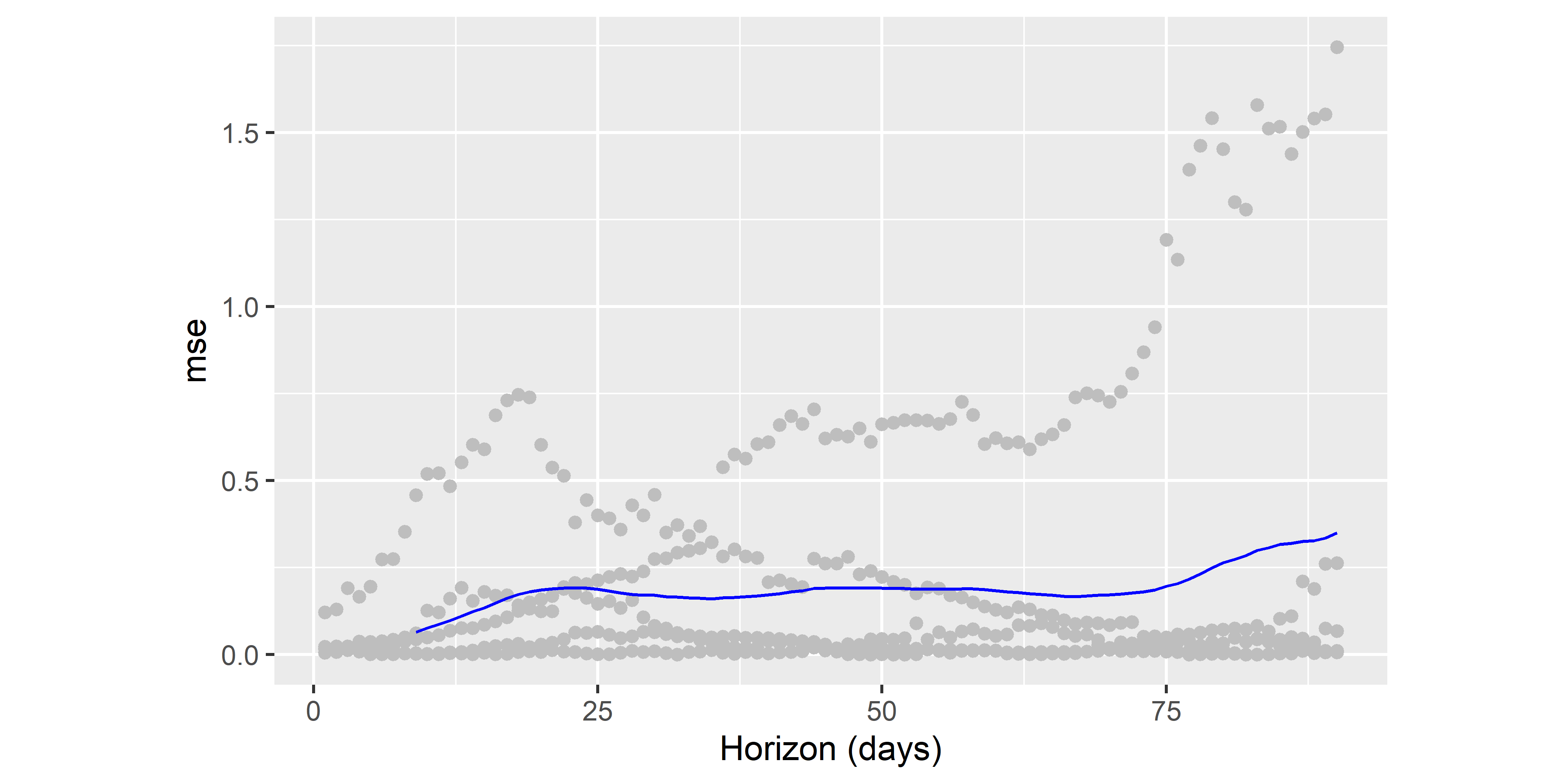
РИСУНОК 6.31: Визуализация метрики качества предсказаний (MSE), полученной по результатам перекрестной проверки модели M3

На рис. 6.31 приведены оценки MSE для каждой из дат прогнозного горизонта ( \(H = 90\) ) каждого из \(K = 5\) блоков данных, участвовавших в перекрестной проверке. Голубая линия соответствует усредненным значениям в пределах каждого скользящего окна размером в 9 наблюдений. Судя по большому разбросу полученных оценок MSE, качество модели M3 желает оставлять лучшего.

6.8.4 Пример выбора оптимальной модели

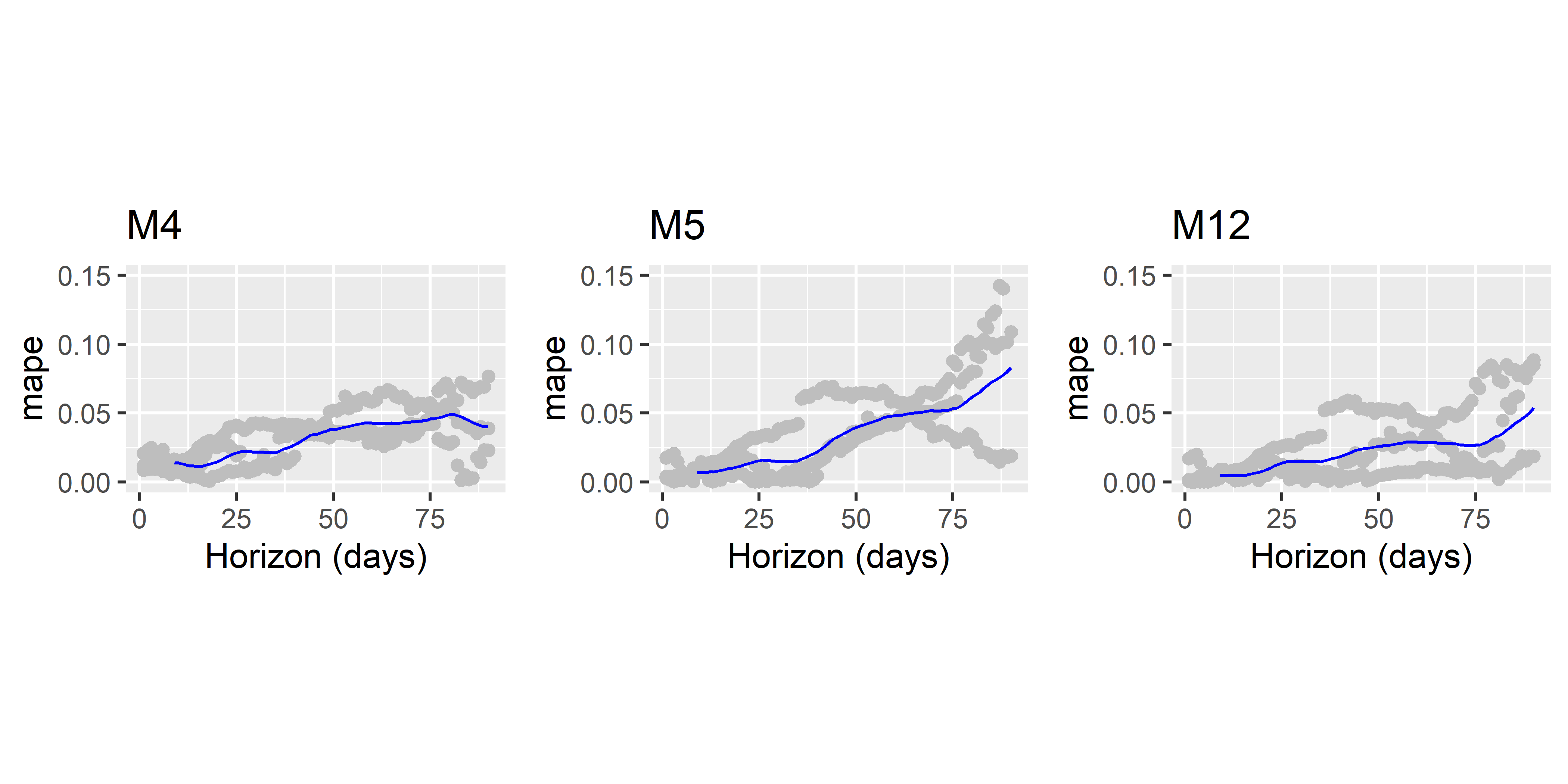
Как видим, M12 лучше других моделей по обеим выбранным метрикам качества. Это можно видеть также из графиков, построенных с помощью функции plot_cross_validation_metric() (рис. 6.32):

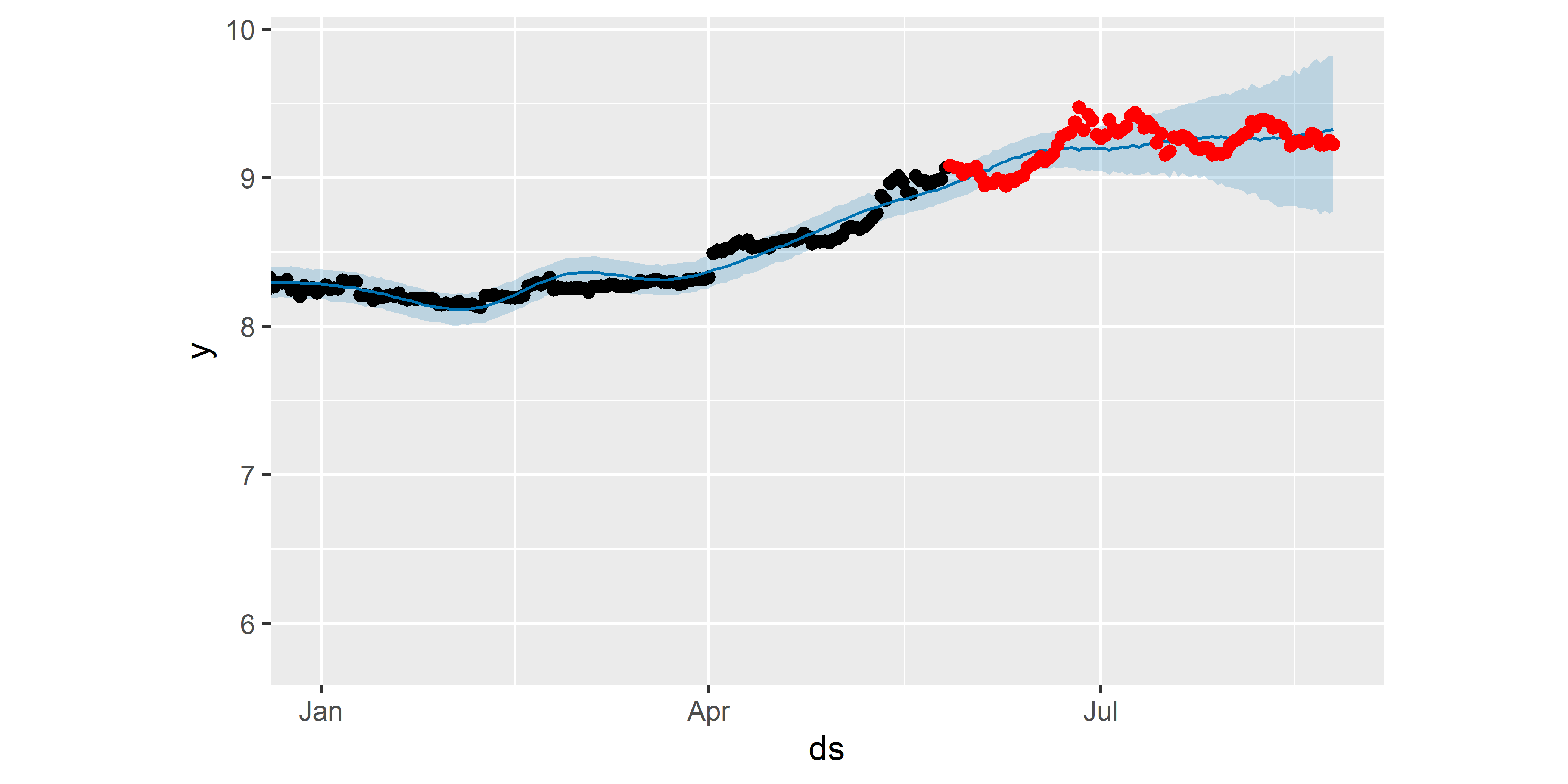
РИСУНОК 6.32: Сравнение качества предсказаний трех моделей по метрике MAPE

Хотя выбранная нами в качестве оптимальной модель M12 не смогла правильно предсказать некоторые локальные колебания стоимости биткоина в прогнозном периоде, в целом она дала неплохой результат: большинство истинных значений стоимости оказалось в пределах 80%–ной доверительной полосы. Однако следует подчеркнуть, что это всего лишь пример использования перекрестной проверки для сравнения качества предсказаний нескольких моделей: совершенно точно не стоит разрабатывать стратегию торговли биткоином на основе приведенных здесь результатов!

6.9 Моделирование емкости системы

Во всех примерах из предыдущих разделов этой главы предполагалось, что моделируемая переменная может расти во времени бесконечно. Однако многие системы имеют естественную “емкость”, выше которой рост невозможен. Классическим примером здесь будет численность популяции какого–либо биологического вида, которая ограничена имеющимися в среде обитания ресурсами. Другой пример — количество пользователей какой–либо онлайн–услуги, которое ограничено доступом в Интернет. Важно отметить, что емкость системы может иметь ограничения и по нижнему порогу (например, численность населения не может быть отрицательной). Одной из особенностей пакета prophet является возможность моделировать временные ряды для подобных систем. Рассмотрим, как это происходит.

6.9.1 Тренд с насыщением

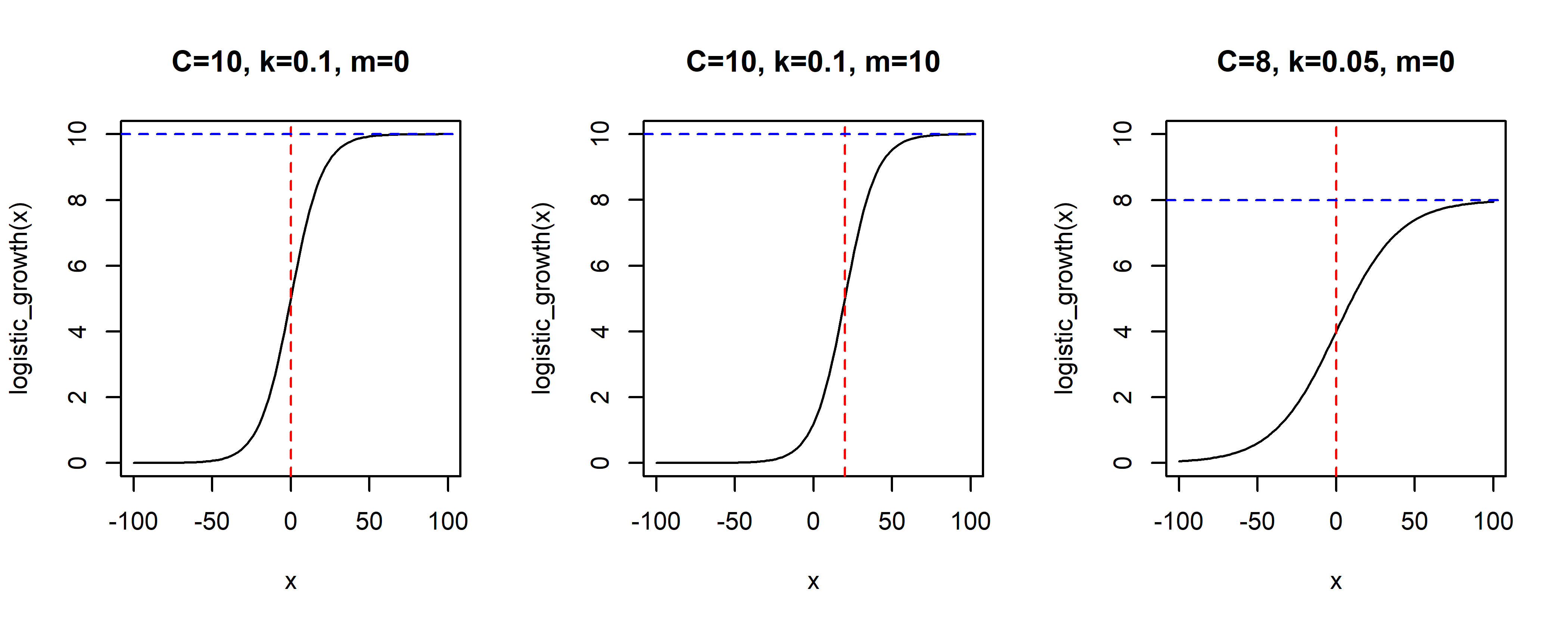
Стандартным подходом для описания роста в системе с ограниченной емкостью является использование логистической функции следующего вида: \[g(t) = \frac<1 + \exp(-k(t-m))>,\] где \(C\) — это верхний порог (емкость системы), \(k\) — скорость роста, \(t\) — время, а \(m\) — параметр, позволяющий “сдвигать” функцию вдоль оси времени. На рис. 6.34 показаны примеры логистической функции с разными значениями параметров.

РИСУНОК 6.34: Примеры логистической функции с разными значениями параметров

6.9.2 Примеры моделей с насыщением тренда

Для начала построим модель, в которой рост зависимой переменной ограничен по некоторому верхнему порогу. Для этого воспользуемся данными по стоимости биткоина за период с января 2016 г. по середину декабря 2017 г., когда наблюдался практически экспоненциальный рост этой переменной (см. рис. 1.3). Предположим, что несмотря на свой экспоненциальный характер роста стоимость биткоина в будущем не могла превысить 11.5 (на логарифмической шкале, что соответствует почти 99000$ (!) на исходной шкале). Для введения этого верхнего порога в модель необходимо добавить новый столбец с (обязательным) именем cap в таблицу с обучающими данными:

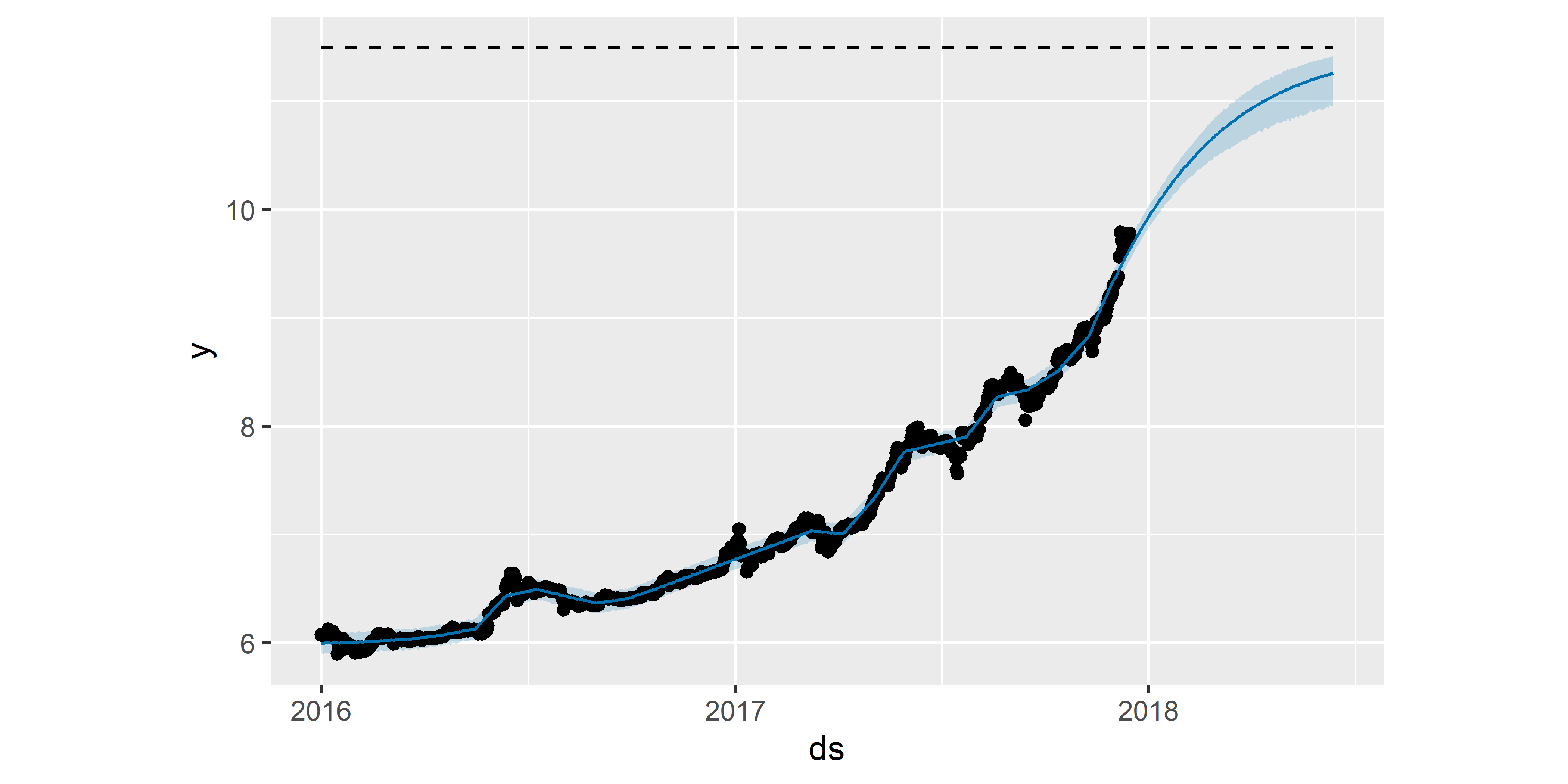
Теперь построим модель по этим обучающим данным (обратите внимание использование аргумента growth = «logistic» при вызове функции prophet() ), рассчитаем прогноз на следующие 180 дней и изобразим полученный результат (рис. 6.35):

РИСУНОК 6.35: Пример модели с верхним порогом тренда

Как видим, несмотря на экспоненциальный рост в историческом периоде, предсказанные значения стоимости биткоина постепенно выходят на плато, что обусловлено введенным в модель ограничением на рост.

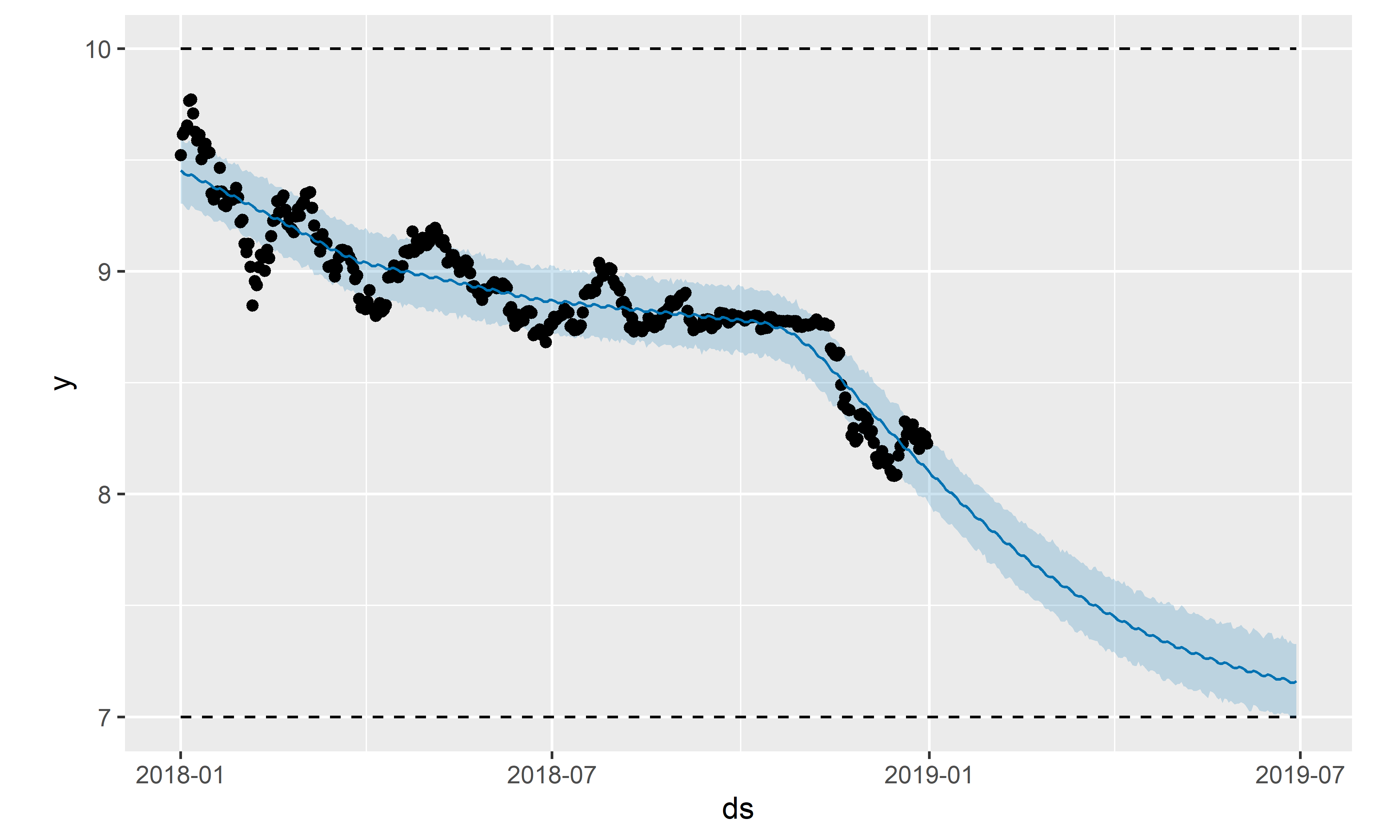
Многие естественные системы имеют ограничения емкости не только по верхнему, но и нижнему порогу (подобно упомянутой выше численности населения). В prophet имеется возможность учесть это обстоятельство путем добавления еще одного столбца — floor — в таблицы с обучающими данными и данными для расчета прогноза (верхний порог при этом также должен присутствовать в обеих таблицах). Для демонстрации этой возможности воспользуемся данными по стоимости биткоина в 2018 г., когда наблюдался выраженный тренд на ее снижение, и построим модель с верхним ограничением тренда cap = 10 и нижним ограничением floor = 7 (рис. 6.36):

РИСУНОК 6.36: Пример модели с нижним порогом тренда

Источник