проверка гипотез о параметрах нормального закона
Математическая статистика
Проверка статистических гипотез
Проверка гипотез о параметрах нормально распределённой генеральной совокупности
Пусть x1,…,xn – выборка наблюдений случайной величины X, имеющей нормальное распределение N(m, σ). Ниже приводятся наилучшие по мощности статистики критерия для различных вариантов гипотез относительно параметров m и s. Как правило, эти статистики связаны с эффективными оценками параметров, относительно которых выдвигаются гипотезы.
1) Гипотеза о значении математического ожидания при известной дисперсии (one-sampled z-test).
В качестве статистики критерия используется статистика
При условии истинности H0 случайная величина
2) Гипотеза о значении математического ожидания при неизвестной дисперсии (one-sample t-test).
В связи с тем, что σ не известно, статистику (1) здесь использовать нельзя. Вместо σ в (1) подставляется оценка S среднеквадратичного отклонения:
при этом в условиях истинности гипотезы H0 статистика Z будет иметь распределение Стьюдента с n–1 степенью свободы.
3) Гипотеза о значении дисперсии при известном математическом ожидании (chi-squared test).
Очевидно, что при условии истинности H0 статистика
4) Гипотеза о значении дисперсии при неизвестном математическом ожидании (chi-squared test).
Очевидно, что при условии истинности H0 статистика
5) Гипотеза о равенстве математических ожиданий при известных дисперсиях (two-sample z-test).
Несложно показать, что при условии истинности H0 статистика
имеет стандартизованное нормальное распределение N(0; 1).
6) Гипотеза о равенстве дисперсий при известных математических ожиданиях (two-sample F-test).
В качестве статистики критерия используется отношение оценок дисперсий при известных математических ожиданиях
7) Гипотеза о равенстве дисперсий при неизвестных математических ожиданиях (two-sample F-test).
В качестве статистики критерия используется отношение оценок дисперсий при неизвестных математических ожиданиях
8) Гипотеза о равенстве математических ожиданий при неизвестных дисперсиях (two-sample unpooled t-test).
Объединённая оценка дисперсии σ 2 по двум выборкам имеет вид:
При условии истинности H0 статистика S 2 имеет распределение
Несложно показать, что статистика
при условии истинности H0 имеет распределение Стьюдента с n1+n2–2 степенями свободы.
б) Оснований считать, что дисперсии генеральных совокупностей равны, нет (Welch’s t-test).
Показано, что при условии истинности H0 статистика Z имеет распределение Стьюдента с числом степеней свободы, равным целой части от величины 1 / k, где
Основные статистики критерия при проверке статистических гипотез о параметрах нормально распределённой генеральной совокупности и их законы распределения приведены в табл. 4.1.
Статистики критерия при проверке статистических гипотез о параметрах нормально распределённой генеральной совокупности
Статистика критерия, Z
Пример 1
Пример 2
Мир статистических гипотез
В современном мире мы обладаем все большим и большим объемом данных о событиях, происходящих вокруг. Зачастую у нас появляются вопросы, на которые хотелось бы быстро ответить на основе имеющейся информации, для этого как нельзя лучше подходит процесс, связанный с проверкой статистических гипотез. Однако, многие считают, что это занятие подразумевает под собой большое число вычислений и в принципе довольно сложно для понимания. На самом деле, алгоритм проверки гипотез достаточно прост, а для осуществления расчетов с каждым годом появляется все больше и больше готовых инструментальных средств, не требующих от человека глубоких познаний в области. Далее я попытаюсь показать, что мало того, что процесс проверки гипотез может быть полезным, так и осуществляется достаточно быстро и без серьезных усилий.
Статистические гипотезы и области их применения
Проверка статистических гипотез является важнейшим классом задач математической статистики. С помощью данного инструмента можно подтвердить или отвергнуть предположение о свойствах случайной величины путем применения методов статистического анализа для элементов выборки. Если в предыдущем предложении какие-либо термины являются не совсем понятными, ниже можно найти пояснение на простом языке.
Для проверки статистических гипотез зачастую применяются статистические тесты, о которых будет рассказано далее.
Алгоритм проверки статистической гипотезы
В обобщенном виде алгоритм выглядит таким образом:
Формулировка основной (H0) и альтернативной (H1) гипотез
Выбор уровня значимости
Выбор статистического критерия
Определения правила принятия решения
Итоговое принятие решения на основе исходной выборки данных
Данные шаги являются унифицированными и схему можно использовать почти во всех случаях. Далее подробнее рассмотрим пример работы данного алгоритма на конкретных данных.
Пример проверки статистической гипотезы
Итак, как вы, наверное, догадались по вышеприведенным примерам, будем проверять гипотезу о том, что имеется существенное различие между числом созданных европейских AI-стартапов в 2019-м и 2020-м годах. Пример достаточно простой, чтобы было проще разобраться в ходе работы алгоритма.
Проверка гипотезы о законе распределения
Для данных 2019-го года проверим нормальность распределения.
H0: случайная величина распределена нормально
H1: случайная величина не распределена нормально
Пусть уровень значимости alpha = 0.05 (как и в 95-ти процентах статистических тестов). Определение уровня значимости достойно отдельного поста, так что не будем заострять на нем внимание.
Будет использован критерий Шапиро-Уилка.
,
,
,
;
Можно сравнить статистику W с критическим значением Wкрит. Критическое значение чаще всего приведено в готовых таблицах (по строкам/столбцам там отмечен объем выборки и уровень значимости, а на пересечении как раз-таки и лежит Wкрит.). Если W>Wкрит., то не отвергаем H0 и наоборот. Но это не очень удобно, поэтому чаще используется второй способ.
Разнообразие статистических критериев
Как мы увидели на примере, важным шагом в проверке статистической гипотезы является выбор критерия. В примере выше я использовала лишь два статистических критерия, но по факту их гораздо больше, так сказать, на все случаи жизни. Данные критерии важно знать и четко нужно осознавать, когда и какой можно применить. Многие из них направлены на сравнение центров распределений случайных величин, например, сравнение средних, медиан, равенство параметра распределения какому-либо числу и т. д. В основном они делятся на параметрические (знаем закон распределения случайной величины) и непараметрические.
Для вашего удобства внизу (рис. 3) приведена таблица с основными, с моей точки зрения, критериями сравнения центров распределения и их классификацией. Надеюсь, она будет вам полезна, ее можно дополнять и расширять по вашему желанию.
Проверка гипотезы о нормальном распределении
Перейти к онлайн решению своей задачи
Решение находим с помощью калькулятора.
Таблица для расчета показателей.
| xi | Кол-во, fi | xi·fi | Накопленная частота, S | (x- x )·f | (x- x ) 2 ·f | (x- x ) 3 ·f | Частота, fi/n |
| 5 | 15 | 75 | 15 | 114.45 | 873.25 | -6662.92 | 0.075 |
| 7 | 26 | 182 | 41 | 146.38 | 824.12 | -4639.79 | 0.13 |
| 9 | 25 | 225 | 66 | 90.75 | 329.42 | -1195.8 | 0.13 |
| 11 | 30 | 330 | 96 | 48.9 | 79.71 | -129.92 | 0.15 |
| 13 | 26 | 338 | 122 | 9.62 | 3.56 | 1.32 | 0.13 |
| 15 | 21 | 315 | 143 | 49.77 | 117.95 | 279.55 | 0.11 |
| 17 | 24 | 408 | 167 | 104.88 | 458.33 | 2002.88 | 0.12 |
| 19 | 20 | 380 | 187 | 127.4 | 811.54 | 5169.5 | 0.1 |
| 21 | 13 | 273 | 200 | 108.81 | 910.74 | 7622.89 | 0.065 |
| 200 | 2526 | 800.96 | 4408.62 | 2447.7 | 1 |
Пример 2. Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n = 200.
Решение.
Таблица для расчета показателей.
Проверка гипотезы о виде распределения
Характеристики распределений
Равномерное распределение
Графическое представление 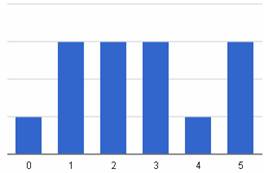 Функция плотности равномерного распределения 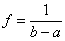 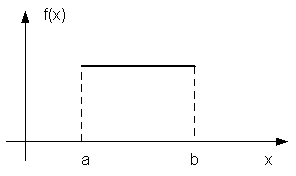 | Математическое ожидание: M[X] = (a+b)/2 Дисперсия: 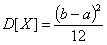 |
Нормальное распределение
Графическое представление 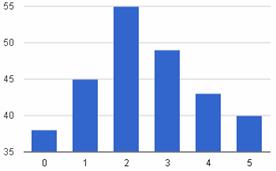 Плотность распределения 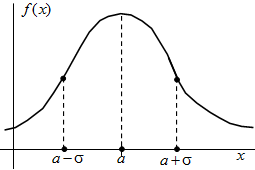 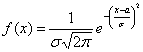 | Математическое ожидание: M[X]=a 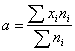 Дисперсия: D[X] = σ 2 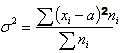 Запись Х |
N( a ; σ) означает, что случайная величина Х распределена по нормальному закону с параметрами a и σ.
Показательное распределение
Графическое представление 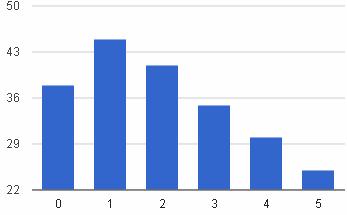 Плотность распределения 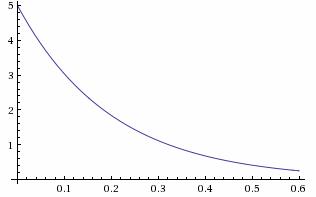 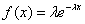 | Математическое ожидание: M[X] = 1/λ Дисперсия: D[X] = 1/λ 2 |
Распределение Пуассона
Биномиальное распределение
Проверка гипотез о виде распределения.
1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
Пример 1. Нормальным или гауссовым распределением называется непрерывное распределение, плотность которого имеет вид
φ(x)– функция Гаусса (таблица),
Параметры a и σ имеют смысл математического ожидания и среднего квадратичного отклонения.
2. Справедливы формулы:
Ф(x)– интеграл вероятностей, таблица.
Обратим внимание, что Ф(-x)=–Ф(x), Ф(x)=0.5 при x>5.
3. Правило трех сигм: P(|X-a|>3ε)=0.0027 – т.е. вероятность отклонения нормально распределенной величины от математического ожидания более чем на 3σ практически равна нулю.
Главная особенность, выделяющая нормальный закон среди других законов распределения, состоит в том, что он является предельным, к которому приближаются другие законы при весьма часто встречающихся условиях.
Выбираем в качестве начала интервала 6.07, так как именно на этот интервал приходится наибольшее количество
Наиболее часто встречающееся значение ряда – 6.16
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше
Таким образом, что 25% единиц совокупности будут меньше по величине 5.86
Q2 совпадает с медианой, Q2 = 6.1
Остальные 25% превосходят 6.26
Децили (децентили)
Децили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 10% единиц совокупности будут меньше по величине D1; 80% будут заключены между D1 и D9; остальные 10% превосходят D9
Таким образом, что 10% единиц совокупности будут меньше по величине 5.76
Каждое значение ряда отличается от другого не более, чем на 0.22
Дисперсия
Среднее квадратическое отклонение
Каждое значение ряда отличается от среднего значения 6.08 не более, чем на 0.25
Коэффициент вариации
Решения задач на проверку статистических гипотез
Проверка статистических гипотез включает в себя большой пласт задач математической статистики. Зная некоторые характеристики выборки (или имея просто выборочные данные), мы можем проверять гипотезы о виде распределении случайной величины или ее параметрах (примеры этих задач на странице Проверка гипотез о параметрах распределения).
В учебных задачах обычно используется следующий алгоритм:
Подробные примеры на разные распределения и критерии вы найдете ниже.
Примеры решений на проверку гипотез онлайн
Критерий Пирсона, нормальное распределение
Пример 1. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X по результатам выборки:
X 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,1 2,3
N 7 9 28 27 30 26 21 25 22 9 5
Пример 2. Были исследованы 200 готовых деталей на отклонения истинного размера от расчетного. Сгруппированные данные приведены в следующей таблице:
По данному статистическому ряду построить гистограмму. По виду гистограммы выдвинуть гипотезу о виде закона распределения (например, предположить, что исследуемая величина имеет нормальный закон распределения). Подобрать параметры закона распределения (равные их оценкам на основе опытных данных). На том же графике построить функцию плотности вероятности, соответствующую выдвинутой гипотезе. С помощью критерия согласия проверить, согласуется ли гипотеза с опытными данными. Уровень значимости взять, например, равным 0,05.
Критерий Пирсона, распределение по закону Пуассона
Пример 3. Отдел технического контроля проверил n партий однотипных изделий и установил, что число нестандартных изделий в одной партии имеет эмпирическое распределение, приведенное в таблице, в одной строке которой указано количество xi нестандартных изделий в одной партии, а в другой строке – количество ni партий, содержащих xi нестандартных изделий. Требуется при уровне значимости α0,05 проверить гипотезу о том, что случайная величина X (число нестандартных изделий в одной партии) распределена по закону Пуассона.
Пример 4. В результате обследования 150 человек были получены данные о количестве приобретаемых за месяц цветных иллюстрированных журналов. Соответствует ли данное распределение закону редких событий Пуассона?
Критерий Пирсона, распределение по показательному закону
Пример 5. В итоге испытаний 1000 элементов на время безотказной работы (час.) получено распределение, приведенное в таблице. Требуется при уровне значимости проверить гипотезу о том, что данные в генеральной совокупности распределены по показательному закону.
Время безотказной работы 0-10 10-20 20-30 30-40 40-50 50-60 60-70
Число отказавших элементов 365 245 150 100 70 45 25
Критерий Пирсона, распределение по равномерному закону
Критерий Колмогорова
Пример 7. Имеются выборочные данные о числе сделок, заключенных фирмой с частными лицами в течение месяца:
— число заключенных сделок 0-10 10-20 20-30 30-40 40-50
— число частных лиц 23 24 11 9 3
Проверить при уровне значимости 0,05, используя критерий согласия Колмогорова, гипотезу о нормальном законе распределения.
Пример 8. В течение месяца выборочно осуществлялась проверка торговых точек города по продаже овощей. Результаты двух проверок по недовесам покупателям одного вида овощей приведены в таблице:Можно ли считать при уровне значимости 0,05, что недовесы овощей являются устойчивым и закономерным процессом при продаже овощей в данном городе (т.е. описываются одной и той же функцией распределения)?
Критерий Вилкоксона
Пример 9. Имеется выборка прибыли коммерческой фирмы за 14 недель до (хi) и после (yi) проведения новой экономической политики. На уровне значимости 0,05 по критерию Вилкоксона проверить гипотезу о том, что введение новой экономической политики в среднем привело к увеличению производительности.
Пример 10. Используя критерий «хи-квадрат» при уровне значимости 0,05, проверить, существует ли зависимость уровня интеллектуального развития учеников от типа школы по результатам обследования 100 сельских и 100 городских школьников:
Тип школы Уровень интеллектуального развития
низкий нормальный высокий
Городская 25 50 25
Сельская 52 41 7
Полезные ссылки
Решебник по математической статистике
Ищете решенное задание на проверку статистических гипотез? Попробуйте тут:

