прямая параллельна плоскости если параметр m равен

Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости

Статья рассматривает понятия параллельность прямой и плоскости. Будут рассмотрены основные определения и приведены примеры. Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.

Параллельные прямые и плоскость – основные сведения

Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.

Параллельность прямой и плоскости – признак и условия параллельности

Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.

Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.

Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.

Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.

Значит, перпендикулярность векторов a → и n → очевидна. Отсюда следует, что прямая с плоскостью являются параллельными.

Ответ: прямая с плоскостью параллельны.

Отсюда следует, что прямая А В с координатной плоскостью О y z не являются параллельными.

Ответ: не параллельны.

Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат О х у z не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:

Система уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.

Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:

Видим, что она не решаема, значит прибегнем к методу Гаусса.

Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.

Ответ: прямая и плоскость параллельны.

Источник

Параметрические уравнения прямой на плоскости: описание, примеры, решение задач

Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.

Вывод параметрических уравнений прямой на плоскости

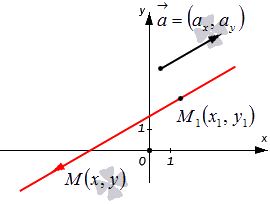
Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.

Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.

В координатной форме оно имеет вид:

Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ

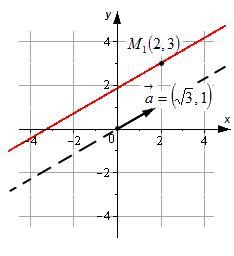
Составление параметрических уравнений прямой на плоскости

Решение

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ

Ответ: x = 2 + 3 · λ y = 3 + λ

Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно

В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.

При этом не должно смущать, если a x или a y будут равны нулю.

Решение

Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:

Решение

Для начала осуществим переход к каноническому уравнению:

Ответ: 3 x + 2 y + 3 = 0

Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.

Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.

Разрешим полученные уравнения относительно переменных x и y :

x = x 1 + a x · λ y = y 1 + a y · λ

Решение

Ответ: x = 2 + 5 · λ y = 2 + 2 · λ

Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.

Решение

Заданное общее уравнение преобразуем в уравнение канонического вида:

Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:

Примеры и задачи с параметрическими уравнениями прямой на плоскости

Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.

Решение

Решение

Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.

Решение

Решение

Решение

Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №4. Параллельность прямых, прямой и плоскости

Перечень вопросов, рассматриваемых в теме

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.

Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл.– М.: Просвещение, 2014. 255 с.

Зив Б. Г. Дидактические материалы. Геометрия 10 кл. – М.: Просвещение, 2014. 96 с.

Глазков Ю. А., Юдина И. И., Бутузов В.Ф. Рабочая тетрадь. Геометрия 10 кл.-М.: Просвещение, 2013. 65 с.

Теоретический материал для самостоятельного изучения

Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого ученого Евклида (3 век до нашей эры), который создал целый труд по математике под названием «Начала». В данной книге есть раздел о параллельных прямых.

В советском энциклопедическом словаре слово «параллельность» переводится с греческого языка, как «идущий рядом».

В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».

В книге «Начала» определение параллельных прямых звучало так «прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются». Это определение почти не отличается от современного.

В области параллельных прямых работало очень много учёных: Н.И. Лобаческий (18-19 век); Аббас ал-Джаухари (работал в Багдаде в 9 веке); Фадл ал-Найризи (Богдад 10 век); Герард (Италия 12 век); Иоганн Генрих Ламберт (Берлин) и многие другие.

Каково расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны) (рис. 1 а, б, в).

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Проиллюстрировать данные определения наглядно нам поможет куб.

Давайте укажем некоторые пары параллельных прямых:

AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.

А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:

AB A₁D₁; AB B₁C₁; CD A₁D₁; CD B₁C₁; BC C₁D₁; BC A₁B₁; AB B₁C₁; AB A₁D₁.

Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.

Аналогично определяется праралельность отрезка и прямой, а так же паралельность двух лучей.

Лемма. Если одна из двух паралельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Если в этой плоскости одна из параллельных прямых b пересекает прямую p, то вторая прямая a тоже пересекает p.

Так как точка N находится на прямой p, то N находится в плоскости α и является единственной общей точкой прямой a и плоскости α.

Нам известно из курса планиметрии, что если три прямые лежат в одной плоскости и две из них параллельны третьей, то эти две прямые параллельны. Похожее утверждение имеет место и для трех прямых в пространстве.

Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Доказательство:

Выберем точку M на прямой b.

Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).

Возможны два случая:

1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.

Пусть прямая b пересекает плоскость α.

Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным. Значит, прямая b находится в плоскости α.

Теперь нужно доказать, что прямые a и b параллельны.

Пусть у прямых a и b есть общая точка L.

Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.

Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.

Если две точки прямой лежат в данной плоскости, то по аксиоме А₂ вся прямая лежит в этой плоскости. Из этого следует, что возможны три расположения прямой и плоскости:

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка-она параллельна плоскости пола.

Теорема (Признак параллельности прямой и плоскости)
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.

Доказательство:
Доказательство проведем от противного. Пусть a не параллельна плоскости α, тогда прямая a пересекает плоскость в некоторой точке A. Причем A не находится на b, так как a∥b. Согласно признаку скрещивающихся прямых, прямые a и b скрещивающиеся.

Мы пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися. Значит, прямая a должна быть параллельна плоскости α.

Существует еще два утверждения, которые используются при решении задач:

Примеры и разбор решения заданий тренировочного модуля

Тип задания: Ввод с клавиатуры пропущенных элементов в тексте

Дано: в ∆ АВС КМ − средняя линия, КМ=5; ACFE- параллелограмм.

Решение: Т.к. КМ − средняя линия, то АС= 2·КМ, то АС=2·7=10

Т.к. ACFE − параллелограмм, то АС=EF=10

Тип задания: Единичный / множественный выбор

Точка М не лежит в плоскости ромба ABCD. На отрезке АМ выбрана точка Е так, что MЕ:ЕА=1:3. Точка F – точка пересечения прямой МВ с плоскостью CDE. Найдите АВ, если AD= 8 cм.

MC

Т.к. AD||BC||FK, следовательно, треугольники MFK и MBC- подобны (по трем углам). Значит

. BC=AD= 8 см;

Источник

Теорема о прямой и параллельной ей плоскости

В школьных учебниках ее и теоремой-то редко называют. Говорят, что это «лемма». Или «следствие». Или «задача». Как будто это что-то необязательное и незначительное. А на самом деле это важнейшая теорема о прямой и параллельной ей плоскости.

Даже если в школе ее доказывают — не говорят, зачем она нужна. Доказали — и забыли.

Но при этом в стереометрии — и особенно в задачах ЕГЭ по математике — есть множество ситуаций, когда без этой важнейшей теоремы не обойтись.

Теорема о прямой и параллельной ей плоскости:

Для чего нам эта теорема? Например, для того, чтобы построить сечение пирамиды плоскостью, параллельной плоскости основания.

1. Постройте сечение тетраэдра плоскостью, проходящей через точки M, N, K. Точка N лежит на ребре

Покажем, что плоскость сечения пересекает плоскость основания пирамиды по прямой NT, параллельной MK.

Прямая MK параллельна AB, лежащей в плоскости основания ABC. Значит,

Плоскость сечения проходит прямую MK, параллельную плоскости ABC. По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и плоскости AВC параллельна прямой MK. Трапеция MKNT — искомое сечение.

Таких задач, где в сечении пирамиды получается трапеция (или параллелограмм), в вариантах Профильного ЕГЭ очень много.

2. В правильной четырехугольной пирамиде PABCD, все ребра которой равны 8, точка K — середина бокового ребра AP.

а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.

б) Найдите площадь сечения.

Пусть точка M — середина AB. Тогда как средняя линия

Пусть точка N — середина PD. Поскольку KN — средняя линия и тогда

Построим сечение пирамиды плоскостью KMN. Пусть плоскости KMN и ABC пересекаются по прямой МE. Покажем, что

По теореме о прямой и параллельной ей плоскости,

б) Найдём площадь сечения.

где — высота трапеции KNEM.

Пусть H — середина KN,

Есть еще одна теорема — такая же полезная, как и теорема о прямой и параллельной ей плоскости. Вот она:

Как ее назвать? Согласитесь, сложно придумать короткое название. Для себя (не для оформления на экзамене!) можно запомнить эту картинку как «домик» или «книжечку». Главное — запомнить формулировку и увидеть, как теорема применяется в решении задач.

Источник

Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости.

В этой статье всесторонне раскрыта тема «параллельность прямой и плоскости». Сначала дано определение параллельных прямой и плоскости, приведена графическая иллюстрация и пример. Далее сформулирован признак параллельности прямой и плоскости, а также озвучены необходимые и достаточные условия параллельности прямой и плоскости. В заключении приведены развернутые решения задач, в которых доказывается параллельность прямой и плоскости.

Навигация по странице.

Параллельные прямая и плоскость – основные сведения.

Начнем с определения параллельных прямой и плоскости.

Прямая и плоскость называются параллельными, если они не имеют общих точек.

Для обозначения параллельности используется символ «». То есть, если прямая a и плоскость параллельны, то можно кратко записать a .

Заметим, что выражения «прямая a и плоскость параллельны», «прямая a параллельна плоскости » и «плоскость параллельна прямой a » одинаково употребимы.

В качестве примера параллельных прямой и плоскости приведем натянутую гитарную струну и плоскость грифа этой гитары.

Параллельность прямой и плоскости далеко не всегда является очевидным фактом. Другими словами, параллельность прямой и плоскости приходится доказывать. Существует достаточное условие, выполнение которого гарантирует параллельность прямой и плоскости. Это условие называют признаком параллельности прямой и плоскости. Прежде чем ознакомиться с формулировкой этого признака, рекомендуем повторить определение параллельных прямых.

Озвучим еще одну теорему, которую можно использовать для установления параллельности прямой и плоскости.

Если одна из двух параллельных прямых параллельна некоторой плоскости, то вторая прямая либо также параллельна этой плоскости, либо лежит в ней.

Определение направляющего вектора прямой и определение нормального вектора плоскости позволяют записать необходимое и достаточное условие параллельности прямой и плоскости.

Это условие удобно использовать для доказательства параллельности прямой и плоскости, которые заданы в прямоугольной системе координат в трехмерном пространстве некоторыми уравнениями.

Разберем решения нескольких примеров.

Являются ли прямая и плоскость параллельными?

Заданная прямая не лежит в плоскости, так как координаты точки прямой не удовлетворяют уравнению плоскости: . Проверим выполнение необходимого и достаточного условия параллельности прямой и плоскости. Очевидно, — направляющий вектор прямой , — нормальный вектор плоскости . Вычислим скалярное произведение векторов и : . Таким образом, векторы и перпендикулярны. Следовательно, заданные прямая и плоскость параллельны.

да, прямая и плоскость параллельны.

Нормальным вектором плоскости Oyz является вектор . В качестве направляющего вектора прямой AB возьмем вектор . Координаты точек начала и конца вектора позволяют вычислить координаты этого вектора, тогда . Проверим выполнение необходимого и достаточного условия перпендикулярности векторов и : . Следовательно, прямая AB и координатная плоскость Oyz не параллельны.

нет, не параллельны.

Разобранное условие не совсем удобно для доказательства параллельности прямой a и плоскости , так как отдельно приходится проверять, что прямая a не лежит в плоскости . Поэтому, доказывать параллельность прямой a и плоскости удобнее с помощью следующего необходимого и достаточного условия.

Пусть прямая a задана уравнениями двух пересекающихся плоскостей ,
а плоскость — общим уравнением плоскости .

Для параллельности прямой a и плоскости необходимо и достаточно, чтобы система линейных уравнений вида не имела решений.

В свою очередь система уравнений не имеет решений, когда ранг основной матрицы системы меньше ранга расширенной матрицы (это следует из теоремы Кронекера-Капелли, при необходимости смотрите статью решение систем линейных уравнений). Несовместность этой системы уравнений можно также показать, используя метод Гаусса для решения систем линейных уравнений.

Докажите параллельность прямой и плоскости .

Перейдем от канонических уравнений прямой к уравнениям двух пересекающихся плоскостей:

Для доказательства параллельности прямой и плоскости покажем, что система уравнений не имеет решения. Воспользуемся методом Гаусса:

Действительно, система уравнений несовместна, следовательно, заданные прямая и плоскость не имеют общих точек. Этим доказана параллельность прямой и плоскости .

Источник