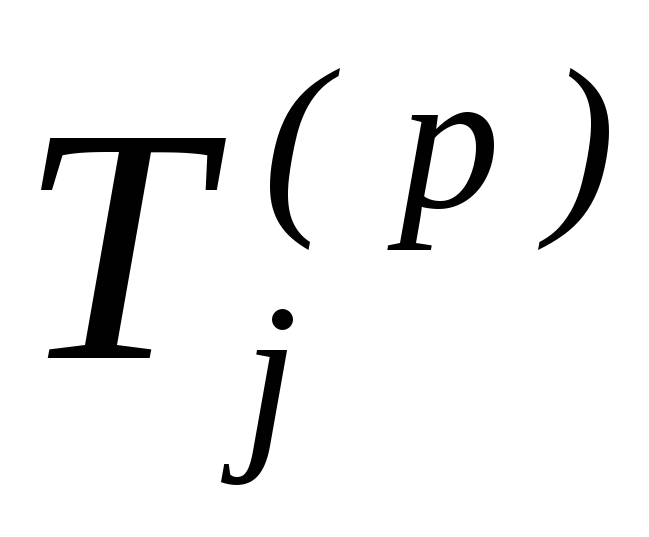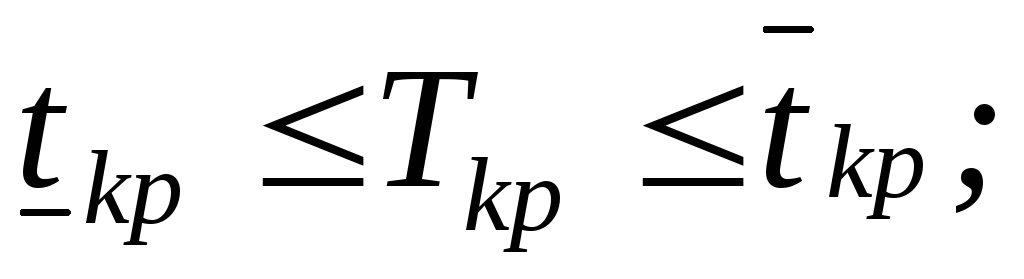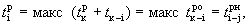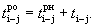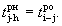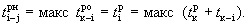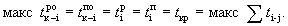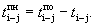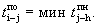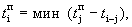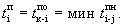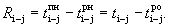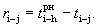расчет параметров сетевой модели

Параметры сетевых моделей и методы их расчета

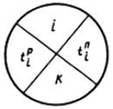
Ранний срок свершения j-го события t_j p — наиболее ранний (минимальный) из возможных моментов наступления данного события при заданной продолжительности работ.

Поздний срок свершения j-го события t_j n — наиболее поздний (максимальный) из допустимых моментов наступления данного события, при котором еще возможно выполнение всех последующих работ в установленный срок.

Ранний срок начала работы t_ij P.H — наиболее ранний (минимальный) из возможных моментов начала данной работы при заданной продолжительности работ. Он совпадает с ранним сроком наступления ее начального события: t_ij P.H = t_j p

Ранний срок окончания работы t_ij P.O — наиболее ранний (минимальный) из возможных моментов окончания данной работы при заданной продолжительности работ. Он превышает ранний срок наступления ее события i на величину продолжительности работы: t_ij P.O = t_i P +t_ij

Поздний срок окончания работы t_ij П.О — наиболее поздний (максимальный) из допустимых моментов окончания данной работы, при котором еще возможно выполнение последующих работ в установленный срок: t_ij П.О = t_j П

Полный резерв времени пути R_(Lп), — показывает, на сколько могут быть увеличены продолжительности всех работ в сумме пути Ln относительно критического пути L_KP: R_(Lп)=t(L_KP)-t(L_П)=T_KP-T_П

Чем ближе коэффициент напряженности к 1,0, тем сложнее выполнять эту работу в установленные сроки.

Методы расчета параметров сетевой модели делятся на две группы.
В первую группу входят аналитические методы, которые включают вычисления по формулам непосредственно на сетевом графике, табличный и матричный методы (см. также метод потенциалов.).
Ко второй группе относятся методы основанные на теории статистического моделирования, которые целесообразно применять при расчете стохастических сетей с очень большим разбросом возможных сроков выполнения работ.

Источник

Графический метод расчета параметров сетевого графика

Рассчитать параметры сетевой модели графическим (секторным) методом можно через калькулятор.

Помимо него существуют следующие способы расчета: табличный метод, метод потенциалов.

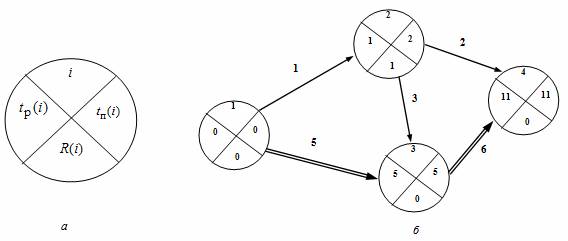
Раннее время свершения события t_p(i) определяется продолжительностью максимального пути max(t) до (i), предшествующего событию i: t_p(i)=max(t) до (i).
Послойно, переходя от исходного события до конечного, определим t_p(i). Всегда для начального события t_p(1)=0.
Для события 3 (рис., б) – t_p(3)=max<1+3,0+5>=5; для события 4 – t_p(4)=max<1+2,5+6>=11.
Длина критического пути L_кр=11. Послойно, переходя от конечного события до начального, определим t_п(i). Всегда для конечного события t_п(4)=t(L_кр)=11. Позднее время свершения события t_п(i) определяется временем достаточным для выполнения работ, следующих за этим событием, т.е. зная продолжительность максимального из последующих за событием i путей max(t) после (i) и продолжительность критического пути t(L_кр), можно найти t_п(i)= t(L_кр)-max(t) после (i).
Для события 2 – t_п(3)=11-max<3+6,2>=2.
Для критического пути время раннего свершения события t_p(i) равно времени позднего свершения этого события t_п(i), т.е. t_p(i)= t_п(i). Зная ранние и поздние сроки свершения событий сетевого графика, легко выявить резерв времени каждого из них R(i)= t_п(i)- t_p(i).
Резерв времени события показывает максимально допустимое время, на которое можно отодвинуть момент его свершения, не вызывая увеличения критического пути. События критического пути резерва времени не имеют.
Связь параметров сетевого графика для событий и работ показана в таблице.

Источник

1.3. Методы расчета параметров сетевой модели

Для расчета параметров сетевых моделей применяют следую­щие три метода:

метод вычислений непосредственно на сетевом графике;

Все эти методы основываются на формулах (1.6), … (1.10) и от­личаются только процедурами вычислений.

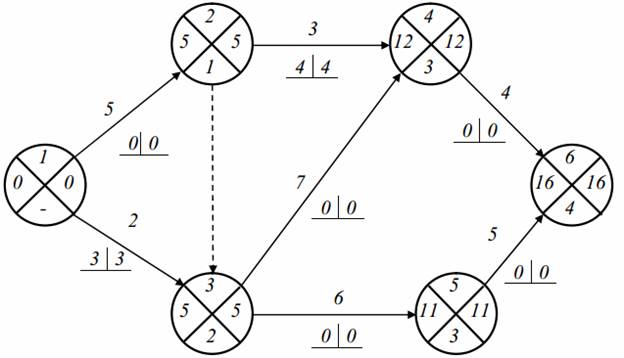
Согласно формуле (1.6) ранний срок наступления данного со­бытия определяется как сумма раннего срока непосредственно предшествующего события и длины дуги (продолжительности ра­боты), которая их соединяет. Если к событию подходят две или большее число дуг, то вычисляют указанные суммы для каждой из входящих дуг; максимальная из сумм и есть ранний срок на­ступления данного события, который записывается в левый сектор. Расчет ведется последовательно от исходящего события к завер­шающему.

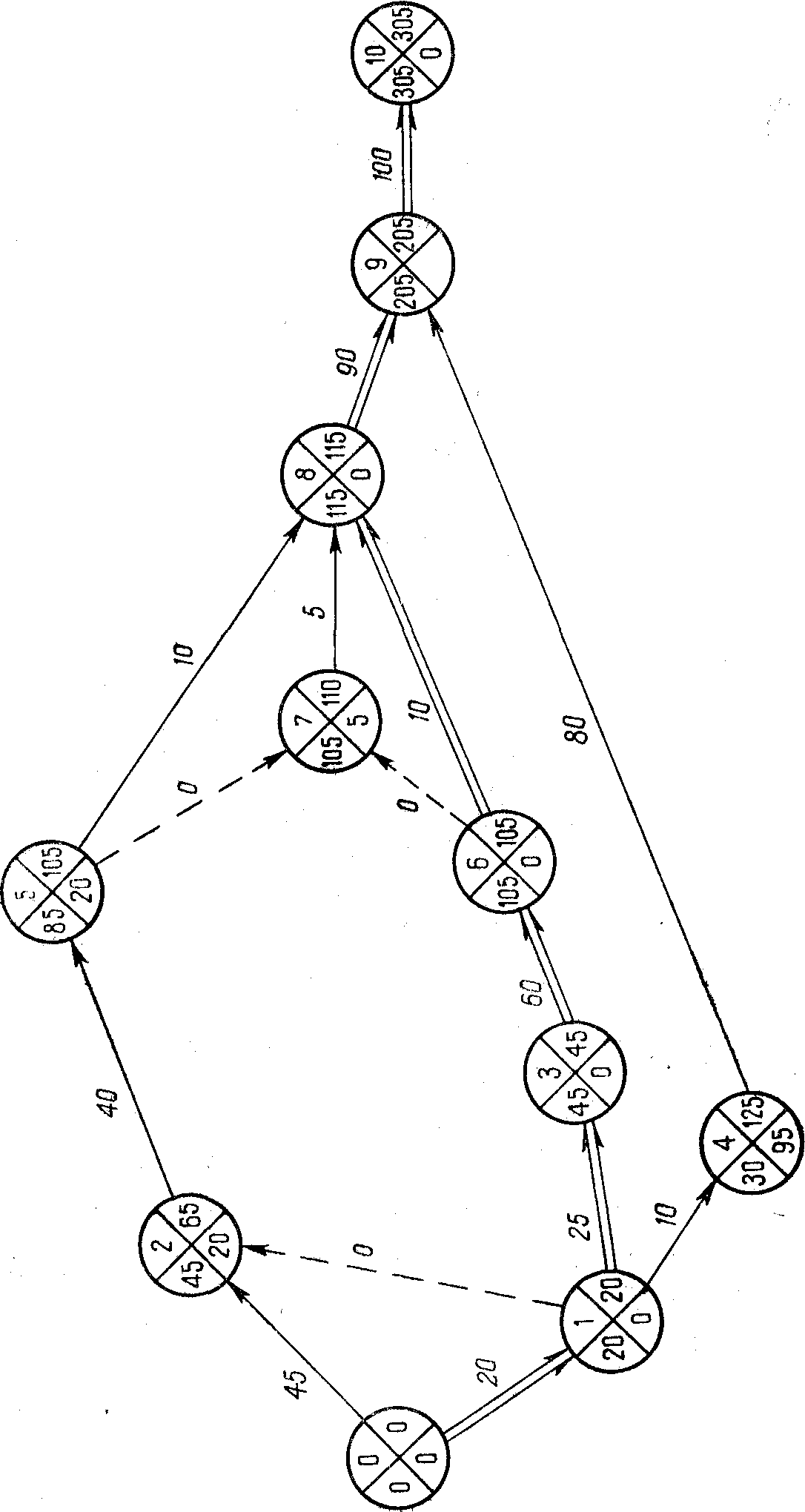
Обратимся к рис. 1.4, на котором изображена та же сетевая мо­дель, что и на рис. 1.3. В левый сектор исходящего события сразу записывается значение T₀ (p) = 0. Далее находим: к событию 1 под­ходит одна дуга (0, 1), поэтомуT₁ (p) = 0+20 = 20; к событию 2 под­ходят две дуги (0, 2) и (1, 2), поэтомуT₂ (p) = max<0+45; 20+0>=45, и так далее Каждое вычисленное значениеT_k (p) сразу записывает­ся в соответствующий сектор.

Для нашего сетевого графика имеем T₁₀ (n) =T₁₀ (p) =305. Далее находим: из событий 9, 8, 7 выходит по одной дуге, поэтомуT₉ (n) = 305–100 =205;T₈ (n) =205–90=115;T₇ (n) =115–5=110;

из со­бытия 6 выходят две дуги (6, 7) и (6, 8), поэтому T₆ (n) = min <110–0; 115–10>=105 и так далее.

После того, как рассчитаны все значения T_k (n) вычисляют ре­зервы времени событий как разности между величинами, записан­ными в левых и правых секторах, и записывают их в нижние сек­торы. Остальные параметры сетевой модели вычисляют, по форму­лам (1.11)–(1.17). Результаты всех расчетов удобно представить в виде табл. 1.2.

Началь­ное со­бытие i

Конеч­ное со­бытие j

Критический путь проходит через события, для которых R_j=0 (0–3–6–8–9–10).

j

Поздний срок

Таблица может быть составлена как по сетевому графику, так и по упорядоченному перечню событий и работ.

Правило определения раннего срока событий вытекает из вы­ражения (1.6) и формулируется следующим образом: ранний срок события с номером j,равен сумме элемента матрицыt_ijс ранним сроком предшествующего события, причем, если предшест­вующих событий несколько, то берется максимальная из сумм, ре­зультат записывается в строку с номеромi=j.

Так как ранний срок нулевого события равен нули, то сразу записывают в нулевую строку значение T₀ (p) =0. Дальше последо­вательно просматриваются столбцы (последующие события), начи­ная с первого (j=1). Из матрицы видим, что событие 1 связано только с одним предшествующим событием, а именно – с нулевым, причемt_0,1=20. Складываемt_0,1со значениемТ₀ (p) = 0, записан­ным в столбцеТ_i (p) по нулевой строке, а результатt_0,1+T₀ (p) = 20 записываем в первую строку в столбецТ_i (p) .Это и будет значе­ниеT₁ (p) .

Переходим ко второму столбцу (j=2). Событие 2 связано с двумя предшествующими событиями: 0 и 1, причемt_0,2=45;t_1,2=0. Составляем две суммыt_0,2+Т₀ (p) = 45+0=45;t_1,2+T₁ (p) = 0+20 = 20 и большую записываем во вторую строку в стол­бецТ_i (p) .

Рассмотрим еще восьмой столбец (j=8). Событие 8 связано с тремя предшествующими событиями 5, 6 и 7. Составляем суммы 10+85=95; 10+105=115; 5+105=110 и в восьмую строку в стол­бецТ_i (p) записываем наибольшую, равную 115.

Правило вычисления позднего срока события следует из выра­жения (2.10) и формулируется следующим образом: поздний срок события с номером i,определяется путем вычитания элемента матрицыt_ijиз позднего срока последующего события, причем, если последующих событий несколько, то берется мини­мальная из разностей; результат записывается в столбец с номе­ромj=i.

Вычисления начинают с завершающего события и сразу запи­сывают в столбец для j=NвеличинуT_N (n) = Т_N (p) .В нашем случае в столбец дляj=10 записываютТ₁₀ (n) =305. Теперь просматриваем последовательно строки, начиная сN–1 (в нашем случае девя­той). Из таблицы видно, что событие 9 связано с одним последую­щим событием 10, причемt_9,10=100. Вычитаем согласно правилу изT₁₀ (n) =305 величинуt_9,10=100 и разность, равную 205, записы­ваем в девятый столбец в строкуТ_j (n) .Это и будет величинаT_9(n)=205.

Переходим к следующей, восьмой строке (i=8). Событие 8, как видно из матрицы, связано с одним последующим событием 9, причемt_8,9=90. Составим разность 205–90=115 и результат за­пишем в восьмой столбец в строкуT_j (n) .

Рассмотрим пятую строку. Событие 5 связано с двумя после­дующими событиями 7 и 8, а соответствующие элементы матрицы t_5,7=0 иt_5,8=10. Составляем две разности 110–0=110; 115–10=105 и меньшую из них за­пишем в пятый столбец в строкуT_j (n) . Это и будетT₅ (n) =105

Остальные параметры вычисляют по формулам (1.11) – (1.17), записывают их в табл. 1.2 и определяют критический путь.

Табличный метод в принципе не отличается от изложенных ме­тодов и преимуществ перед ними не имеет.

Теперь обратимся к сетевым моделям, у которых продолжи­тельности работ являются случайными величинами. В этом случае продолжительность критического пути также является случайной величиной; сохраним за ней обозначение Т_кр. Исходная инфор­мация таких моделей содержит сеть, законы распределения веро­ятностей величинt_ij(или вероятностные оценкиa_ij, b_ij,m_ij) и (но не обязательно) директивный срок наступления завершающего событияТ_дир.

Основными задачами анализа этих моделей являются:

– определение среднего значения и дисперсии критического времени T_кр;

– определение закона распределения величины T_кр;

– определение таких сроков наступления событий, которые с заданной вероятностью не будут превышены;

– определение законов распределения для моментов наступле­ния событий;

– определение вероятности прохождения критического пути через данную работу или совокупность работ.

Существующие аналитические методы решения перечисленных задач весьма громоздки и не нашли практического применения. Более широкое применение получил метод статистических испы­таний.

Далее излагается практически удобный для расчетов метод ве­роятностной оценки наступления завершающего события. Необхо­димо подчеркнуть, что вероятностный анализ для завершающего события особенно важен, поскольку для продолжительности вы­полнения комплекса, как правило, устанавливается директивный срок и характер распределения случайного реального завершения комплекса работ по отношению к директивному сроку может суще­ственно влиять на принятые решения при управлении выполнением комплекса.

Рассмотрим следующие задачи вероятностного анализа сверше­ния завершающего события:

– определить вероятность того, что продолжительность крити­ческого пути (выполнения комплекса работ) T_крлежит в задан­ных пределах

– определить вероятность того, что продолжительность крити­ческого пути не превысит заданный директивный срок;

– определить такой директивный срок, который с заданной ве­роятностью не будет превышен.

В методе приняты некоторые допущения, из которых выделим два основных:

1. Дисперсия D_крвеличины критического времени зависит толь­ко от дисперсий работ, лежащих на критическом пути.

2. Величина T_крраспределена по нормальному закону. Это допущение основывается на предположении, что число работ крити­ческого пути достаточно велико и что продолжительности этих работ являются независимыми случайными величинами. Согласно центральной предельной теореме сумма достаточно большого числа независимых случайных величин, сравнимых по дисперсии, при­ближенно распределена по нормальному закону.

Расчет для всех задач начинается с вычисления математических ожиданий продолжительностейt_ijдля всех работ комплекса по формуле (1.1) или (1.3). Затем, оперируя величинамикак детерминированными:

– вычисляют продолжительность критического пути , представляющую собой математическое ожидание случайной величиныT_кр;

– определяют критический путь L_кр;

– вычисляют дисперсии D_ijпродолжительностей работ, лежащих на критическом пути, по формуле (1.2) или (1.4);

– на основании известной теоремы, что дисперсия суммы независимых величин равна сумме дисперсий слагаемых, находят дисперсию продолжительности критического пути

. (1.18)

Теперь при сделанных допущениях можно решить первую из перечисленных выше задач, а именно – определить вероятность того, что продолжительность критического пути лежит в заданных пределах: |

, (1.19)

где – функция Лапласа ;

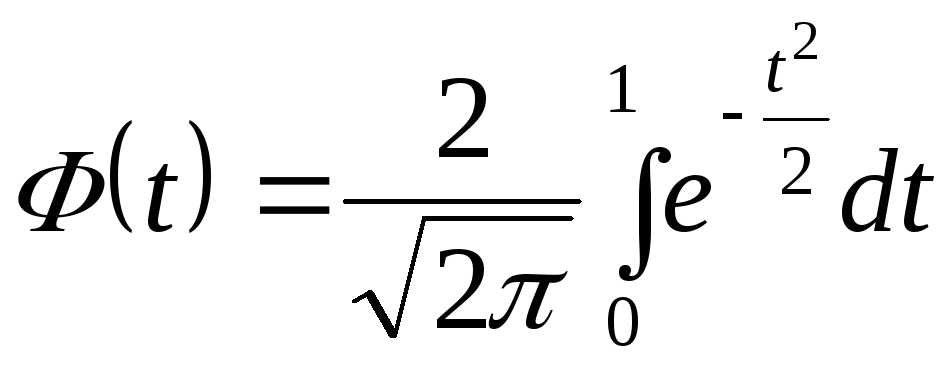
t – аргумент функции Лапласа ;

– математическое ожидание случайной величиныТ_кр;

.

Перейдем ко второй задаче. Согласно принятому допущению случайная величина Т_крраспределена по нормальному закону, по­этому на основании правила трех сигм можно написать

. (1.20)

Очевидно, что директивный срок должен лежать в тех же пре­делах:

. (1.21)

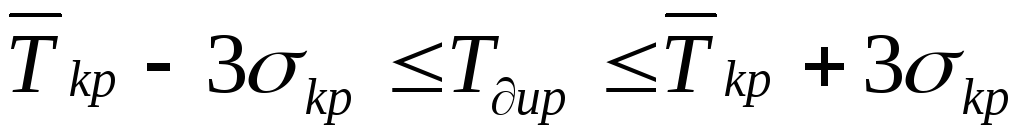
Действительно, если то вероятность выпол­нения комплекса работ равна нулю; если же взятьто без оснований будет растянут срок выполнения комп­лекса.

Кроме того, должно выполняться условие

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

РАСЧЕТ ПАРАМЕТРОВ СЕТЕВОЙ МОДЕЛИ

5.1. Продолжительность работы t_i-j дает представление о длительности отдельной работы, но не увязывает ход выполнения отдельных работ сетевого графика с ходом выполнения программы в целом.

Такая увязка предполагает достижение двух целей. Она должна определять положение отдельной работы по отношению к началу программы в рамках заданных графических характеристик сети и установленной длительности работ и давать представление о возможном перемещении работ по программе и возможном изменении продолжительности работ. Последнее связано с возможным перераспределением ресурсов, поскольку продолжительность выполнения той или иной работы зависит от уровня концентрации ресурсов на соответствующем участке СМР. Увязка отдельной работы со всем ходом работ достигается при расчете сетевой модели, который заключается в определении следующих временных параметров:

раннее начало работы ;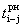

раннее окончание работы ;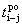

раннее время свершения события ;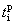

позднее начало работы ;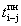

позднее окончание работы ;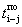

позднее время свершения события ;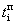

5.2. Расчет перечисленных параметров сетевой модели следует начинать с определения ранних сроков выполнения каждой из работ и событий.

Так как каждое событие может свершиться только тогда, когда будут выполнены все входящие в него работы, наиболее раннее время его свершения определяют той из всех входящих в событие работ, которая заканчивается последней, т.е.

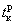
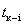
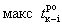
где — раннее время свершения каждого из предшествующих событий;

— продолжительность каждой входящей в событие работы;

— максимальное значение раннего окончания работ, предшествующих рассматриваемому событию.

Расчет раннего времени нужно начинать с исходного события, время свершения которого принимается равным нулю. При табличном методе расчета сетевого графика определяются ранние сроки начала и окончания каждой работы. При этом расчет следует вести сверху вниз, а сроки начала и окончания работы определять совместно. Раннее окончание работы равно раннему началу плюс продолжительность работы:

Ранний срок начала работы (работ), выходящей из исходного события, равен нулю.

Раннее начало последующей работы равно раннему окончанию данной работы:

Если данной работе предшествует несколько работ, то ее раннее начало следует принимать равным максимальному значению из всех ранних окончаний предшествующих работ, но оно равно, как было указано выше, раннему сроку свершения предшествующего события

В результате расчета должен быть определен ранний возможный срок свершения завершающего события или раннее возможное окончание последней завершающей цикл работы; тем самым определен наиболее продолжительный путь из всех, соединяющих исходное и завершающее событие, и наиболее ранний возможный срок окончания комплекса работ. Этот путь называют критическим, а его продолжительность обозначают T_кр. В сложном графике таких путей может быть несколько.

Максимальное значение раннего окончания, приходящееся на какую-либо работу (или работы) из числа работ, входящих в завершающее событие, определяет одновременно и позднее окончание и продолжительность критического пути.

Поздние сроки остальных работ и событий определяются от завершающего события к исходному. Позднее начало любой работы определяется как разность значений ее позднего окончания и продолжительности самой работы:

Если за данной работой следует не одна, а несколько работ, то ее позднее окончание будет равно минимальному значению из всех поздних начал последующих работ:

Самое позднее время свершения любого события сетевой модели должно быть таким, чтобы все последующие работы были бы выполнены без нарушения времени свершения завершающего события, следовательно, для всех других событий:

где 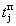— позднее время свершения каждого из последующих событий;

Аналогично определению ранних сроков расчет поздних сроков свершения событий можно также не производить, они могут быть определены по поздним срокам окончания работ:

5.4. Затем следует определить резервы времени: полный резерв R_i-j и частный резерв r_i-j.

Полный резерв времени, работы, т.е. максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы, не изменяя срока выполнения всего комплекса, определяется разностью между одноименными позициями и ранними сроками работы

Частный резерв времени работы, т.е. максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы, не изменяя срока раннего начала последующих работ, определяется как разность раннего начала последующей работы и раннего окончания данной

Рис. 8. Четырехсекторное деление события

Методика разработки сетевого графика на процесс проектирования.

Составление технологической схемы процесса проектирования.

На основе здания определяется состав проекта на различных стадиях
проектирования. Технология проектирования позволяет одновременно
выполнить несколько частей проекта, некоторые из них связаны между собой
и зависят друг от друга. Эти связи и последовательность выполнения частей
проекта выражаются в сетевой модели. Принятая технология проектирования
определяет топологию сетевого графика. Составление сетевого графика
начинается с процесса разработки генплана участка или с технологической
части проекта, или с первого варианта разработки архитектурно-
строительной части, в зависимости от особенностей проектируемого объекта.
Затем выполняются разработки по специальным работам: отопление и
вентиляция, водоснабжение и канализация, электрооборудование,
слаботочные работы, автоматизация и сигнализация, механизация и
транспорт, газоснабжение и т.д. Эти работы выполняются одновременно.

Завершив специальные части проекта, окончательно отрабатывается и
корректируется архитектурно-строительная часть проектируемого объекта.
Заканчивают проектные работы разработкой проекта организации
строительства (ПОС), составление сметной документации и расчетом
технико-экономических показателей (ТЭП).

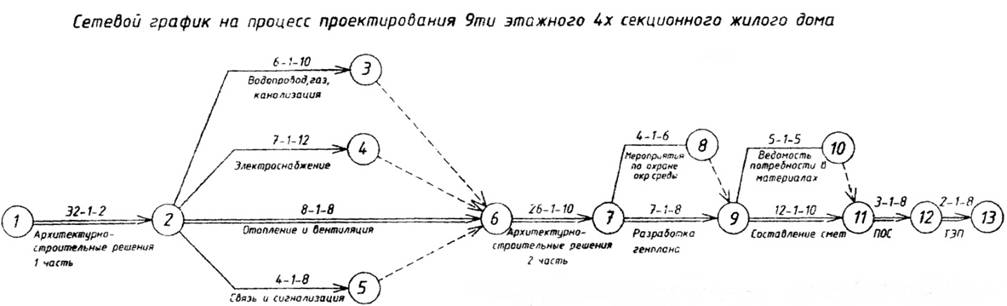
Топологию сетевого графика для проектирования заданного ему объектастудент должен обосновать самостоятельно. На рис. 3 показан примерсетевой модели процесса проектирования объекта.

4.1.2. Определение сметной стоимости, трудоемкости, количества
исполнителей и продолжительности выполнения частей проекта.

После разработки сетевого графика на процесс проектирования в процентахот общей стоимости проекта определяется стоимость частей проекта.

По стоимости проектирования отдельных частей проекта и плановой
выработки на проектных работах определяется трудоемкость выполнения
каждой части проекта. Сроки проектирования отдельных частей проекта
устанавливаются исходя из общего срока составления проекта, места части
проекта в общей технологической схеме процесса проектирования и
численного состава проектировщиков. Состав группы исполнителей-
проектировщиков рекомендуется из 3-8 человек в зависимости отспециализации работ. Полученные расчетные данные о стоимости,
трудоемкости, сроках выполнения работ и количестве исполнителей сводятся
в табл. 3.

Карточка-определитель работ сетевого графика на процесс проектирования.

4.1.3. Расчет сетевого графика, его календаризация и оптимизация.

Расчет сетевого графика осуществляется секторным методом.

Полученное значение продолжительности принимаемого пути определяетвремя, необходимое для разработки заданного проекта при данном составеисполнителей.

Следующим этапом работы является календаризация сетевого графика,
которая выполняется путем привязки работ сетевого графика в линейной
форме к шкале времени. Причем календаризация осуществляется по ранним
срокам работ.

Начинать календаризацию следует с работ, лежащих на критическом пути отисходного до завершающего события. Затем на календарный график
наносятся все остальные работы в очередности, соответствующей шифру
работ. Для работ, имеющих частные резервы времени, обозначенные
пунктиром, указывается сроки резерва. Над работой указывается численность
его исполнителей.

Состав проекта и относительная стоимость разработки проектной
документации в процентах от стоимости проектирования 9-ти этажей 4х

секционного жилого дома.

4. Водоснабжение, канализация, горячее водоснабжение, газоснабжение
-6%

9. Составление ведомостей потребностей в материалах – 2%

10.Разработка ПОС – 2%

Карточка определитель работ и ресурсов сетевого графика на процесс

Таблица расчета сетевого графика

Источник

• ← расчет параметров серверного оборудования 1с
• расчет параметров силового трансформатора →