расчет параметров усеченного конуса

Калькуляторы расчета размеров развертки конуса

Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса

Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.

Калькуляторы расчета размеров развертки конуса

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

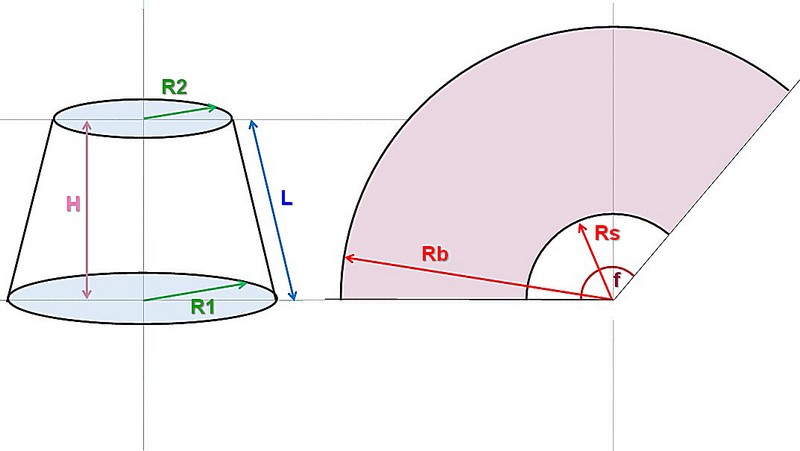
Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

Шаг 1 – определение длины образующей L

(Если она уже известна – шаг пропускается)

Шаг 2 – определение радиусов внутренней и внешней дуги развертки

Радиусы рассчитываются поочередно – с выбором в соответствующем поле калькулятора.

Источник

Исходный полный конус

Прежде чем говорить об усеченном объекте и его характеристиках, следует рассмотреть исходную фигуру, из которой он получается.

Пусть имеется некоторая замкнутая кривая, лежащая в произвольной плоскости. Это может быть окружность, эллипс или любая другая линия с плавными перегибами. Пусть также существует отрезок, который не лежит в плоскости указанной замкнутой кривой. Если в пространстве зафиксировать некоторую точку, а затем соединить ее с любой точкой на кривой, то получится образующая будущего конуса. Если теперь ее перемещать вдоль замкнутой кривой одним своим концом, в то время как другой конец будет зафиксированным в точке, то она опишет коническую поверхность.

Это геометрическое построение позволяет получить объемную фигуру конус, которая состоит из следующих элементов:

Существующие виды

В геометрии известны несколько видов конуса. Каждый из них определяется характером директрисы и расположением относительно нее генератрисы. Выделяют следующие виды фигуры:

Круглая прямая фигура

Получить этот конус несложно. Необходимо взять прямоугольный треугольник, поставить его на один из катетов и вращать вокруг второго катета, который будет являться осью, а его длина — высотой для объемной фигуры. Катет, на котором стоит треугольник, является радиусом круглого основания конуса.

С полученной фигурой легко работать при решении геометрических задач, поскольку для нее существуют довольно простые формулы для площади поверхности и объема.

Площадь S фигуры состоит из двух частей: основания и боковой поверхности. С помощью простых геометрических рассуждений можно показать, что сумма этих частей выражается в виде такой формулы: S = pi*r 2 + pi*g*r, где число pi=3,14, r — радиус окружности в основании, g — длина генератрисы. В разрезе на плоскости коническая поверхность представляет собой сектор круга радиусом g.

Объем рассматриваемого конуса выражается следующей формулой: V = 1/3*pi*r 2 *h. Здесь h — высота фигуры. Можно заметить, что величина V ровно в три раза меньше аналогичной для цилиндра, имеющего то же основание, что и конус. Записанную формулу может вывести любой школьник, который знаком с интегральными вычислениями.

Усеченный геометрический объект

Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.

Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.

Способы построения

Можно выделить два основных способа построения усеченного круглого геометрического объекта:

В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной. Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.

Второй способ получения усеченного конического объекта связан с использованием фигуры трапеции прямоугольного типа. Такая трапеция представляет собой два параллельных отрезка, которые имеют длины a и b. Они соединены одним перпендикуляром h и косым отрезком g.

Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.

Площадь поверхности

Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:

S = S1 + S2 + Sb = pi*r1 2 + pi*r2 2 + pi*g*(r1 + r2).

Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.

Формула объема

Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:

V = 1/3*pi*r1 2 *H — 1/3*pi*r2 2 *(H-h).

Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:

V = 1/3*pi*h*(r1 2 + r2 2 + r1*r2).

Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:

V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).

Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.

Пример решения задачи

Из данных задачи можно определить значение каждого радиуса. Для этого необходимо ввести следующее равенство: r1 = 2*r2. Тогда для суммы площадей оснований можно записать выражение:

Откуда получается:

r2 = (S/(5*pi))^0,5 = (100/(5*3,14))^0,5 = 2,52 см.

Тогда радиус большего основания будет равен r1 = 2*r2 = 5,04 см.

Чтобы найти генератрису g усеченного конуса, следует рассмотреть прямоугольный треугольник, который образован двумя катетами: высотой h и отрезком r1-r2. Его гипотенуза является генератрисой, она равна:

g = ((r1-r2)^2 + h 2 )^0,5 = (2,52 2 + 15 2 )^0,5 = 15,21 см.

Поскольку известны все необходимые линейные параметры усеченной фигуры, можно воспользоваться известной формулой для площади ее боковой поверхности:

Таким образом, усеченный конус является фигурой вращения, поверхность которой состоит из оснований и боковой части. Чтобы воспользоваться формулами для определения его площади и объема, необходимо знать любые три его линейных параметра.

Источник

Площадь и высота усеченного конуса

Свойства

Если даны площади оснований усеченного конуса, то не составит труда найти радиус оснований, а затем их диаметр и периметр по стандартным формулам окружностей. r=√(S_r/π) R=√(S_R/π) d=2√(S_r/π) D=2√(S_R/π) p=2√(πS_r ) P=2√(πS_R )

Теперь, зная высоту и радиусы оснований усеченного конуса, необходимо найти апофему, используя внутреннюю прямоугольную трапецию. Построив в ней дополнительный прямоугольный треугольник, можно вычислить апофему по теореме Пифагора, где катетами будут высота и разность радиусов оснований. Из этого же треугольника можно через тангенс найти угол при большем основании, и отняв его из 180 градусов по правилу суммы углов трапеции найти угол между апофемой и меньшим основанием. l=√(h^2+(R-r)^2 )=√(h^2+(√(S_R )-√(S_r ))^2/π) cos⁡β=(R-r)/l=(√(S_R )-√(S_r ))/(l√π) α=180°-β

Чтобы найти плoщадь боковой поверхности усеченного конуса, понадобятся не только значения радиусов окружностей, лежащих в его основаниях, но и апофема, найденная выше по теореме Пифагора. Площадь полной поверхности усеченного конуса будет включать в себя вычисленную площадь боковой поверхности и площади оснований. S_(б.п.)=πl(R+r)=l(√(πS_r )+√(πS_R )) S_(п.п.)=S_(б.п.)+S_r+S_R=l(√(πS_r )+√(πS_R ))+S_r+S_R

Чтобы найти объем усеченного конуса, также понадобятся высота и площади оснований, которые в соответствующем алгебраическом виде дадут нужный результат. V=h/3 (S_r+√(S_r S_R )+S_R )

Источник

Конус, как напечатать картинку?

Этот вопрос возникает при сублимационном термотрансфере на конические предметы, например, кружку латте или при прямой печати на сувенирных принтерах.

Бумажный или пластиковый стаканчик

Самый распространенный конический предмет, с которым сталкиваются абсолютно все люди — это стаканчик. Он может быть бумажным или пластиковым, с принтом или без, но неизменным остается одно — это форма! Коническая фома стаканчика была выбрана не просто так, она имеет неоспоримое преимущество перед цилиндрической.

Форма конуса позволяет вставлять один стаканчик в другой, тем самым получается сформировать компактную упаковку из десятков изделий. Форма цилиндра не позволяет этого сделать. Итак, подобная конусообразная форма делает удобнее хранение, транспортировку и реализацию стаканчиков.

Однако, при необходимости напечатать картинку на конусообразном предмете, возникают некоторые технические и дизайнерские сложности. Сразу обращаю ваше внимание, что стаканчик является усеченным конусом, и далее рассматриваемый способ подготовки принта для печати, будет основан именно на построении макета усеченного конуса и подходит для любых подобных предметов, например, для кружек латте.

Развертка усеченного конуса

Для правильной печати прямоугольного изображения на конусе, нам нужно наложить его на развертку усеченного конуса и деформировать в соответствии со сторонами развертки.

Построение развертки

Есть как минимум два способа построения: ручные расчеты и программные. Для первого способа можно воспользоваться стандартными геометрическими формулами.

Ручной расчет

Программный расчет

Воспользуемся бесплатным сервисом Templatemaker (© Ideogram). Перейдем в раздел Cone (truncated) внесем в поля нужные нам значения.

Построение принта

В векторной программе

Искажение растровых и векторных объектов для печати кружек латте с помощью Corel Draw 2018 и инструмента “Envelope” (Конверт)

В растровой программе

В специализированных САПР

PACKZ – Warping & 3D Conical cups

Warp artwork on conical labels with Studio

Инструкция по работе с Boxshot 5 для создания Conical Labels

Источник

Что такое усеченный конус: определение, основные элементы

В данной публикации мы рассмотрим определение и основные элементы усеченного конуса. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение усеченного конуса

Усеченный конус (конический слой) – это геометрическая фигура в пространстве; часть конуса, оставшаяся между его основанием и секущей плоскостью, параллельной этому основанию.

Примечание: В рамках данной публикации мы будем рассматривать самый распространенный вид усеченного конуса – прямой круговой.

Усеченный конус образуется путем вращения на 360° прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию, или равнобедренной трапеции вокруг своей оси симметрии на 180°.

На рисунке ниже конус образован путем вращения равнобедренной трапеции ABCD вокруг оси O₁O₂.

Основные элементы усеченного конуса

Развёртка боковой поверхности усеченного конуса выглядит следующим образом:

Длина бОльшей (меньшей) дуги равна длине окружности соответствующего основания конуса ( 2πR или 2πr ).

Источник