расчет первичных параметров симметричного кабеля

Расчет первичных и вторичных параметров кабеля

Цель работы

Изучение конструкций и характеристик симметричных междугородных (магистральных) и зоновых кабелей связи, ознакомление с образцами кабельной продукции различных типов, получение навыков по расчету первичных и вторичных параметров.

Эскизы поперечных сечений предложенных кабелей

Рисунок 1 – Симметричный кабель междугородней связи

Рисунок 2 – Симметричный кабель зоновой связи

Расчет первичных и вторичных параметров кабеля

Таблица 1 – Исходные данные симметричного кабеля

1 Активное сопротивление симметричной кабельной цепи переменному току учитывает сопротивление постоянному току, а также увеличение сопротивления за счет поверхностного эффекта в проводниках симметричной цепи, эффекта близости и потерь на вихревые токи в соседних металлических элементах:

где ‒ сопротивление постоянному току одной жилы двухпроводной линии на 1 км;

‒ удельное электрическое сопротивление стали;

‒ коэффициент укрутки проводников;

‒ коэффициент, учитывающий тип скрутки;

мм ‒ диаметр неизолированной жилы;

мм ‒ расстояние между центрами жил;

‒ температурный коэффициент сопротивления;

‒ температура;

‒ специальные функции, полученные с использованием видоизмененных функций Бесселя, определяются из таблицы 2 по вычисленному значению величины :

.

Таблица 2 – Функции Бесселя

kr	F(kr)	G(kr)	H(kr)	Q(kr)
0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 7,0	0,00036 0,00519 0,0258 0,0782 0,1756 0,318 0,492 0,678 0,862 1,042 1,743 2,799	(kr) 4 /64 0,000975 0,01519 0,0691 0,1724 0,295 0,405 0,499 0,584 0,669 0,755 1,109 1,641	0,0417 0,042 0,053 0,092 0,169 0,263 0,348 0,416 0,466 0,503 0,530 0,596 0,643	0,9998 0,997 0,937 0,961 0,913 0,845 0,766 0,686 0,616 0,556 0,400 0,286
>10

Таблица 3 – Значение специальных функций в соответствии с частотами

Таблица 4 – Зависимость сопротивления пары от частоты

Рисунок 3 ‒ Зависимость сопротивления пары от частоты

2 Индуктивность симметричной кабельной цепи определяется суммой внешней L_вш и внутренней L_вт индуктивностей:

где ‒ относительная магнитная проницаемость стали;

мм ‒ радиус неизолированной жилы;

‒ вспомогательная функция, определяемая из таблицы 2.

Таблица 5 – Зависимость индуктивности пары от частоты

Рисунок 4 ‒ Зависимость индуктивности пары от частоты

3 Емкость симметричного кабеля с учетом близости соседних пар и влияния наружной металлической оболочки определяется по формуле:

где ‒ эквивалентная относительная диэлектрическая проницаемость изоляции;

‒ поправочный коэффициент, характеризующий близость металлических проводников, определяется по формуле:

,

где ‒ диаметр парной скрутки, мм;

‒ диаметр изолированного проводника, мм;

‒ диаметр голого проводника, мм.

Тогда при любых частотах.

Рисунок 5 ‒ Зависимость емкости пары от частоты

4 Проводимость изоляции может быть вычислена по формуле:

,

где ‒ сопротивление изоляции кабеля;

‒ эквивалентная величина тангенса угла диэлектрических потерь, определяется из таблицы 6.

Таблица 6 – Зависимость tgδ_э от типа кабеля и частоты

Таблица 7 – Зависимость проводимости изоляции от частоты

f, кГц
G, См/км

Рисунок 6 – Зависимость проводимости изоляции от частоты

5 Волновое сопротивление в общем случае определяется выражением

.

В области высоких частот (при f>40 кГц) волновое сопротивление можно определить по формуле:

.

Таблица 7 – Зависимость модуля волнового сопротивления от частоты

f, кГц
, Ом/км	693,16503	426,44867	356,24031	315,63486

Рисунок 7 – Зависимость модуля волнового сопротивления от частоты

6 Электромагнитная энергия, распространяясь вдоль линии связи, уменьшается по величине и изменяется по фазе от начала к концу линии. Коэффициент затухания и коэффициент фазы в общем виде определяются по формуле расчета коэффициента распространения. Коэффициент распространения является комплексной величиной и может быть определен суммой действительной и мнимой ее частей:

.

7 В области высоких частот коэффициент затухания можно определить по формуле:

Таблица 8 – Зависимость коэффициента затухания от частоты

f, кГц
, дБ/км	3,2481455	15,006062	27,916114	46,313311

Рисунок 8 – Зависимость коэффициента затухания от частоты

8 В области высоких частот коэффициент фазы можно определить по формуле:

.

Таблица 9 – Зависимость коэффициента фазы от частоты

f, кГц
, дБ/км	0,8649333	5,3212388	11,112942	21,661755

Рисунок 9 – Зависимость коэффициента фазы от частоты

9 Скорость распространения электромагнитной энергии является функцией частоты и фазовой постоянной, которая в свою очередь зависит от первичных параметров линии. В общем виде она определяется по формуле:

.

Таблица 10 – Зависимость скорости распространения энергии от частоты

f, кГц
, км/с	72643,582	118077,49	141348,38	159532,41

Рисунок 10 – Зависимость скорости распространения энергии от частоты

Вывод

Рекомендуемые условия эксплуатации — в грунтах I — III групп, в телефонной канализации, трубах, блоках и по мостам (кабели с покровом Шп) или непосредственно в грунтах всех групп без мерзлотных деформаций и не агрессивных к стальной броне (кабели с покровом Бп); в грунтах всех групп кроме вечномерзлых, при пересечении несудоходных и несплавных рек в районах с повышенным электромагнитным влиянием линий высокого напряжения (кабели с покровом БпШп).

Анализируя полученные зависимости первичных и вторичных параметров данного кабеля от частоты, можно сделать вывод, что его использование на частотах свыше 100 кГц не эффективно.

Источник

Расчет первичных параметров передачи симметричных кабелей

К первичным параметрам передачи относятся: активное сопротивление, индуктивность кабеля, емкость кабеля, проводимость изоляции.

Первичные параметры передачи не зависят от величины тока или напряжения, а определяются только конструкцией кабеля, используемыми материалами и частотой тока. Данные параметры полностью определяют электрические свойства кабелей связи и качество передачи.

4.2.1 Расчет сопротивления цепи

Для высокочастотных симметричных кабелей связи активное сопротивление (Ом/км), рассчитывается по формуле

(4.1)

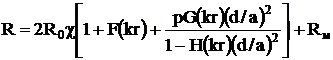
χ = 1,02—1,07 коэффициент укрутки;

Таблица 4.2 – Коэффициенты F, Q, H и G для различных значений kr

Kr	F	G	H	Q
	0,0417
0,5	0,000326	0,000975	0,042	0,9998
1,0	0,00519	0,01519	0,053	0,997
1,5	0,0258	0,0691	0,092	0,987
2,0	0,0782	0,1724	0,169	0,961
2,5	0,1756	0,295	0,263	0,913
3,0	0,318	0,405	0,348	0,845
3,5	0,492	0,499	0,416	0,766
4,0	0,678	0,584	0,466	0,686
4,5	0,862	0,669	0,503	0,616
5,0	1,042	0,755	0,530	0,556
7,0	1,743	1,109	0,596	0,400
10,0	2,799	1,641	0,643	0,282
>10,0			0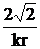

Коэффициент вихревых токов, 1/мм рассчитывается по формуле

(4.2)

где — круговая частота;

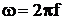
σ – проводимость материала, МСм/м.

Значения параметра kr для различных материалов проводников приведены в табл. 4.3.

Таблица 4.3- Параметры проводниковых материалов

Металл	ρ, Ом·мм 2 /м	σ, МСм/м	k, 1/мм	kr
Медь	0,0175	57,0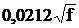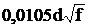
Алюминий	0,0295	34,36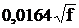
Сталь	0,1380	7,23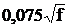
Примечание: d-диаметр проволоки, мм; f – частота, Гц.

Для расчета активного сопротивление жилы постоянному току можно использовать формулу

(4.3)

Если жилы многопроволочные, то активное сопротивление цепи постоянному току определяется как

(4.4)

Дополнительное сопротивление R_м, эквивалентное потерям в окружающих металлических элементах кабеля, зависит от месторасположения рассматриваемой цепи, материала оболочек, частоты и определяется экспериментально (табл.4.4). В таблице приведены значения R_м при частоте 200 кГц. Пересчет на другие частоты

(4.5)

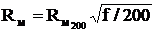
где R_м200 – значение из табл.4.4.

Таблица 4.4 – Дополнительное сопротивление R_м за счет потерь в

окружающих металлических массах

Для алюминиевой оболочки ввиду его большой проводи­мости сопротивление потерь будет меньше в 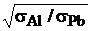, т. е. в 2,72 раза.

4.2.2 Расчет индуктивности кабеля

Индуктивность кабеля (Гн/км), складывается из двух составляющих: внутренней и межпроводниковой (внешней)

(4.6)

χ – коэффициент укрутки;

μ₀— относительная магнитная проницаемость металла жилы;

Внешняя индуктивность имеет большое значение (порядка 60..90 %). Внутренняя индуктивность по абсолютной величине значительно меньше внешней и с ростом частоты существенно снижается.

4.2.3 Определение емкости цепи

Для двухпроводной цепи расчетная формула рабочей емкости (Ф/км), с учетом влияния соседних цепей, оболочки и скрутки цепей имеет вид

(4.7)

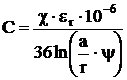
Расчетные формулы для определения коэффициента ψ различных типов скрутки имеют вид:

(4.8)

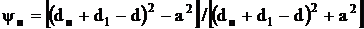
для звездной без экрана

(4.9)

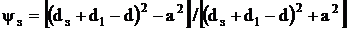
где 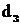— диаметр звездной скрутки;

для звездной в экране

(4.10)

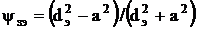
где d_э – диаметр экрана;

для двойной парной скрутки

(4.11)

4.2.4 Определение проводимости изоляции

Проводимость изоляция на переменном токе обусловлена как током проводимости, так и активной составляющей тока абсорбции, причем роль последнего с повышением частоты заметно возрастает. Проводимость изоляции (См/км), определяется по формуле

(4.12)

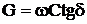
tgδ – тангенс угла диэлектрических потерь.

Значения ε и tgδ для различных видов изоляции и частот приведены в табл. 4.5.

Сведений о значениях tgδ в более высоком диапазоне частот для симметрич-

ных кабелей в технической литературе не имеется, однако, учитывая, что чистые полиэтилен и полистирол имеют значение tgδ постоянное в широком диапазоне частот и потери определяются лишь наличием в изоляции примесей и загрязне-

ний неполярного диэлектрика полярными молекулами при расчете в более высоком диапазоне частот tgδ можно принимать равным его величине при f=550 кГц.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник

Расчет первичных параметров передачи цепи симметричного кабеля

Контрольное задание №1

Тема: Расчет первичных и вторичных параметров симметричных и коаксиальных кабелей.

Рассчитать в заданном диапазоне частот первичные и вторичные параметры передачи цепи симметричного (коаксиального) кабеля. Расчет указанных параметров выполняется на 5 частотах, равномерно распределенных в заданном диапазоне, начиная с f_н до f_в. В заключение построить графики частотных зависимостей рассчитанных параметров. Исходные данные приведены в табл.

Исходные данные :

Расчет первичных параметров передачи цепи симметричного кабеля

Расчет параметров передачи цепи выполняется для симметричного кабеля звездной скрутки.

Активное сопротивление цепи переменному току симметричного кабеля звездной скрутки вычисляется по формуле:

, (1.1)

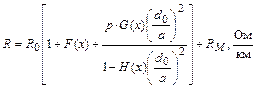
где 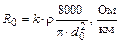– сопротивление двухпроводной симметричной кабельной цепи постоянному току;

d₀ – диаметр токопроводящей жилы, мм;

p – коэффициент, учитывающий тип скрутки элементарной группы, для звездной скрутки p=5;

k – коэффициент скрутки, в расчетах принимается равным 1,02;

r – удельное сопротивление материала токопроводящей жилы (r_меди = 0,0175 и r_{алюминия} = 0,028) Ом×мм 2 /м.

Аргумент x функций F(x), G(x) и H(x) в (1.1) определяется по формулам:

x = 0,0105 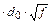– для медных токопроводящих жил,

x = 0,0022 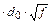– для алюминиевых токопроводящих жил,

Значения функций F(x), G(x) и H(x) определяются по табл. 1.3. Если значение аргумента x не совпадает с приведенными в табл. 1.3 значениями, то для нахождения истинных значений функций следует использовать линейную интерполяцию.

Для звездной скрутки элементарной группы расстояние между центрами токопроводящих жил

где d₁ – диаметр изолированной жилы.

Значение d₁ для сплошной изоляции токопроводящих жил:

где d₀ – диаметр токопроводящей жилы; t_из – толщина изоляции.

Значение d₁ для кордельной изоляции токопроводящих жил:

где d_к – диаметр корделя, t_л – толщина ленты.

Точный расчет значений R_М в формуле (1.1) вызывает определенные трудности, поэтому при решении данной задачи рекомендуется использовать упрощенную формулу:

(1.2)

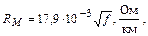
Расчет индуктивности двухпроводной кабельной цепи выполняется по формуле:

(1.3)

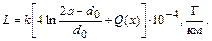
Значение Q(x) определяется по табл. 1.3.

Емкость кабельной цепи

, (1.4)

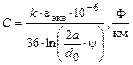
Где e_экв – эквивалентная диэлектрическая проницаемость, значения которой для различных типов изоляции приведены в табл.1.4;

y_зв » 0,65 – поправочный коэффициент для звездной скрутки.

Проводимость изоляции кабельной цепи

, (1.5)

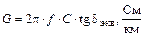
где tg d_экв – эквивалентное значение тангенса угла диэлектрических потерь изоляции.

Расчет:

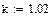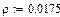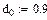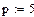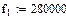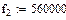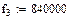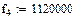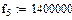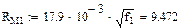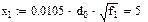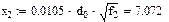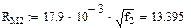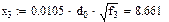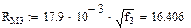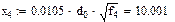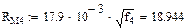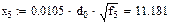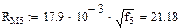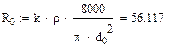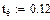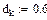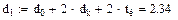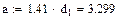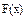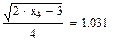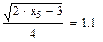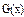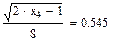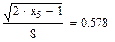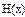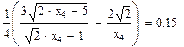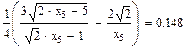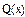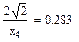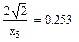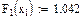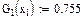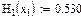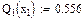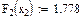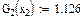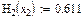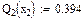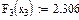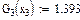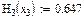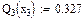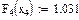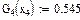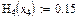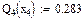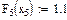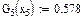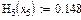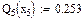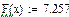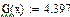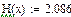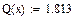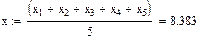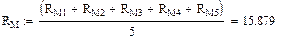Значения функций F(x), G(x), H(x) и Q(x) определили по следующим формулам, так как аргумент (x) не совпадает с приведенными в табл. значениями.

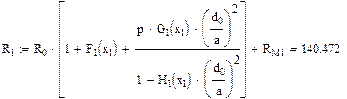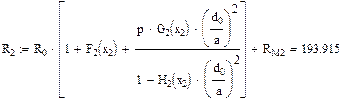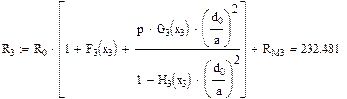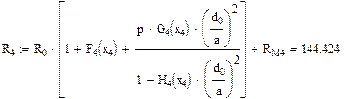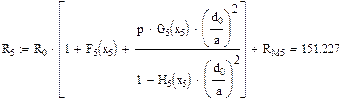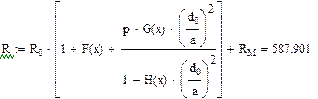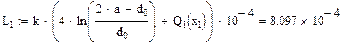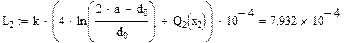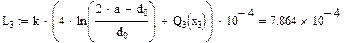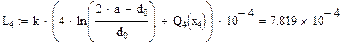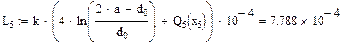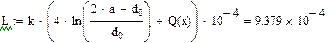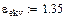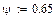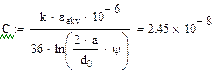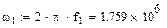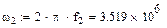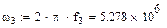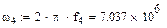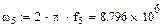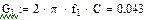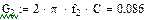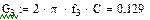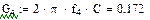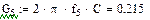Графики частотных зависимостей рассчитанных параметров:

Источник