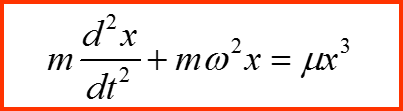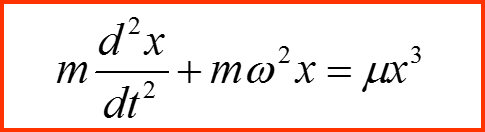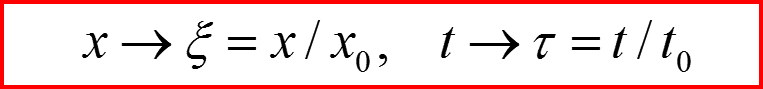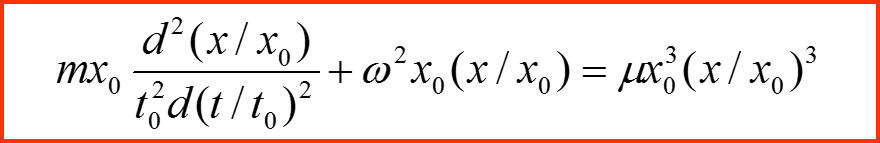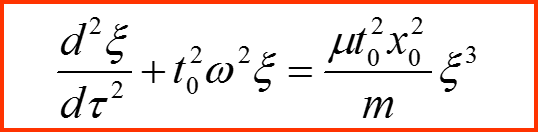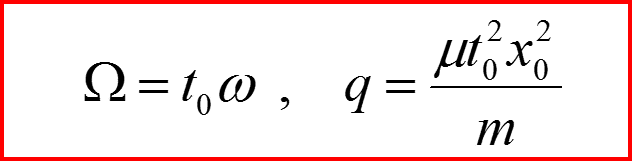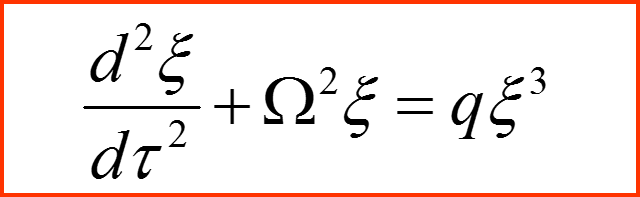разложение по малому параметру

Метод малого параметра

Метод малого параметра

Боголюбова, Ю. А. Митропольский. Напишите желаемое периодическое решение в следующем формате х-ХL iLXl ntxi … 2 часа дня. Где x0, xi x-неизвестная периодическая функция частот, кратных циклическим частотам p и p, определяемая later. At одновременно разверните p — 2 нужной круговой частоты-с мощностью малого параметра p. п а АИП ПДП… 3 часа дня. Где ocj, a4-постоянный коэффициент, который определяется при интегрировании Формулы 1.

При вычислении момента инерции однородной плоской фигуры относительно некоторой оси выделяют в плоской фигуре такую элементарную площадь, момент инерции которой относительно соответствующей оси известен, либо легко может быть подсчитан. Людмила Фирмаль

Значения Oj, a выбираются таким образом, чтобы решение 2 было периодическим, то есть не содержало так называемых резонансных или долговременных членов, которые растут бесконечно с time. To для ясности предположим, что при решении задачи необходимо интегрировать дифференциальные уравнения. У1 п х м грех ст НТ грех 3 ПТ… Коэффициент Mt зависит от at. Среди конкретных решений этого уравнения есть бесконечно возрастающее резонансное решение-cos pt. To чтобы искомый закон движения был цикличным, необходимо учесть M равное нулю. Искомый коэффициент a определяется по формуле Mi 0. Решите задачу указанным методом и определите следующий закон свободных нелинейных колебаний.

Рекомендуется в следующем порядке 1 Создайте дифференциальное уравнение движения 1, представленное в виде—p f x 0. 2 используя формулы 2 и 3, в разложении мощности малого параметра p опишем искомый закон движения x и неизвестную мощность 2 круговой частоты p. 3 вычислить I и I, используя формулу 2 4 заменить значения x, I и I в абзаце. 2 и 3 подраздел 1 дифференциал equations. At в то же время замените коэффициент а с помощью Формулы 3.То есть, ki-pt-a1p, — a ii— …И еще write. As результатом этих подстановок является дифференциальное уравнение с членами, содержащими малый параметр p различной степени obtained. In кроме того, без членов p А. А. Андронов, А. А. Вит, О. Е.

Используя начальные условия 7, интегрируем дифференциальное уравнение X0 p9×0 0 и x0 0 9 ввести полученную формулу xe t в дифференциальное уравнение я Р Х Fi в ОИ. х0 После простой тригонометрии с правой стороны мы получаем следующую форму п Х2 l1x потому что ПТ потому что 3 ф… Чтобы не увеличиваться бесконтрольно со временем, его следует считать равным нулю. Определите C из уравнения 0. 10 используя начальные условия движения в пункте 7 интегрировать дифференциальное уравнение А Х1 Н COS на 3 ПТ… определите xj f.

Значения x0 0, ots и x1 0-это пункт 8, 9 и 10 вставить в дифференциальное уравнение А Р2 1 ф я а ХV ХД. Повторите расчет, а также расчет абзаца. 9 и 10, А и Х2 0 и т. д 12 определите искомые значения x 0 и p9, пункт 2 и введите расчетные значения xv 0, aj Xj 0, a2, x2 0 и т. д При решении задачи строки 2 и 3 обычно усекаются терминами, включающими p или A. ниже приведен пример х х0 jxx1 p2×2, Р2 А2 СА1 п a9. Задача 20.2.Используя метод малых параметров, определите уравнение физического маятника конечной амплитуды и частоту круговых колебаний, если P — его вес. I-расстояние от оси подвески z до центра тяжести см. рисунок, а 1-момент инерции маятника относительно подвески axis.

До члена, содержащего малый параметр p первого порядка, уравнение принимает вид Fo 4-R Fo I F1 F1 1fo-FY 0. а также коэффициенты в скобках без p, если мы уравняем члены уравнения без p до нуля ФО Фо О, 8 Ф1 ргУ1 1фо Ф5 — 9 Учитывая начальные условия t 0, p aQ, 0, используя уравнение 0 Фо 0 нф1 0 О О Ф О нФ О пиши ФО 0 ЛF1. О Фо о ЛF1 о. В каждом из этих уравнений члены без p и с p слева и справа делаются равными начальным условиям функций 0 0 и 1. ФО 0 АО. Ф1 О. ФО О. Ф1 0 0.

Если в ходе решения задачи требуется вычислить момент инерции твердого тела относительно оси, не проходящей через центр тяжести, то проводят параллельную ось через центр тяжести твердого тела и применяют теорему Штейнера (при этом момент инерции твердого тела относительно оси, проходящей через центр тяжести, масса твердого тела и расстояние между параллельными осями должны быть известны). Людмила Фирмаль

Где формула 12 имеет вид i p4i 4a8cos3P О4 Его общее решение fx равно сумме F1 f, 11 f, 1, 15 Где f — частное решение уравнения 14, а f 1 — общее решение соответствующего однородного уравнения F1 p ph1-0.In это дело Ф Ф 1 Ди cospt да грех, пт, ТП Альф соз 3 ПТ Ф И f — Если вы назначите 9apcos 3pt формуле 14, вы найдете a — atsthr1.Теперь общее решение 15 можно записать следующим образом Форекс ДХ, потому что ПТ да грех пт-потому что 3 ПТ 16 Функция 16 и ее производная по времени —DJ slnjrf d2pcos RF — sin3pf Начальные условия движения 10 7 0, 0 0, 1 0 0, поиск.

Как видно из Формулы 20, маятник колеблется по закону 20 на частоте кривизны Р 18, которая зависит от начального отклонения маятника А0.Поэтому вибрации нет isochronous. In другие слова Условия эксплуатации. Напомним, что приближенное линейное дифференциальное уравнение A p 0 соответствовало изохронным гармоническим колебаниям 3 p a0cos6f. поэтому даже приближенное решение нелинейных уравнений, выполненных в этой задаче, смогло обнаружить отсутствие изохронности колебаний. Влияние начального углового отклонения маятника a0 на круговую частоту p равно small.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Квазиклассическое приближение. Разложение по малому параметру

Страницы работы

Содержание работы

На сколько близки классическая и квантовая картины механики?

Разложение по малому параметру

Что такое малый параметр?

I. Общий метод малого параметра

При каких условиях правую часть можно считать малой добавкой? Для ответа на этот вопрос уравнение необходимо оберазмерить!!

I. Общий метод малого параметра

Обезразмеривание – это процедура приведения всех параметров задачи к выбранным стандартным масштабам:

Пусть величины x0 и t0 являются некоторыми стандартными масштабами

I. Общий метод малого параметра

Переменные ξ и τ называются безразмерными переменными. Уравнение, представленное в безразмерных переменных содержит исключительно безразмерные коэффициенты и называется обезразмеренным:

I. Общий метод малого параметра

Постоянные Ω и q являются безразмерными:

I. Общий метод малого параметра

Для безразмерных параметров неравенство: q

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Иллюстрированный самоучитель по Maple 9

Приближенные методы решения дифференциальных уравнений. Метод разложения по малому параметру.

Решать уравнения Eq_0, Eq_1 и Eq 2 следует строго в той последовательности, в какой они вводились. Причина очевидна – каждое последующее уравнение содержит, помимо неизвестной функции, еще и функции, которые определяются предыдущими уравнениями.

Переходим непосредственно к решению уравнений. Однако прежде сделаем некоторые замечания относительно начальных условий. В общем случае начальные условия также следует раскладывать в ряд по малому параметру. Коэффициенты разложения определяют начальные условия для уравнений, соответствующих тем же степеням параметра порядка. В данном случае малый параметр в начальных условиях не присутствует, поэтому начальным условием для уравнения нулевого порядка автоматически становится у0(х), а начальные условия для у1(х) и у2(х) – нулевые, поскольку отсутствуют (т.е. равны нулю) коэффициенты, начиная с первого порядка, разложения начальных условий в ряд по малому параметру.

Итак, получаем следующее.

Ниже, согласно полученному решению, выполняется присваивание.

Внимание!
В этом месте функция у0(х) «технически» становится переменной!

Ситуация такая же, как и с функцией у(х). Например, если ввести команду у0(х), получим ожидаемый результат.

Однако если в приведенном выше вызове изменить аргумент (y0(t)), нужного значения (1/t) не получим.

Решаем теперь уравнение Eg 1 и находим y1(x).

В данном случае, перед присваиванием, раскладываем выражение для y1(x) на сумму дробей (процедура expand(%)).

Наконец, находим у2(х). Последовательность действий такая же.

Источник

Иллюстрированный самоучитель по Maple 9

Приближенные методы решения дифференциальных уравнений. Метод разложения по малому параметру.

Преобразуем это уравнение, перенеся все слагаемые, содержащие малый параметр, в левую часть, а слагаемые, не содержащие малый параметр, – в правую. Сделать это можно с помощью процедуры isolate(). При вызове процедуры вычислительным ядром Maple предпринимается попытка в равенстве или алгебраическом выражении, указанном первым параметром, выразить подвыражение, указанное вторым параметром, т.е. фактически указанное первым параметром выражение решается относительно второго параметра-выражения.

Таким образом, получаем следующее.

Теперь можно собрать слагаемые при соответствующих степенях малого параметра (epsilon).

Неизвестные функции y0(x), y1(x) и у2(х) выбираются так, чтобы коэффициенты при степенях малого параметра (не всех, а только до второго включительно, до которого раскладывается в ряд искомая функция) равнялись нулю.

Отсюда получаем первое уравнение (для определения у0(х)), приравняв правую часть уравнения Eq (это коэффициент при нулевой степени параметра epsilon) к нулю.

Приравнивая к нулю коэффициент при первой степени малого параметра, получаем еще одно уравнение.

В этом уравнении, помимо y1(x), присутствует и у0(х). Поэтому, прежде чем решать уравнение Eq_1, необходимо сначала решить уравнение Eq 0, найти тем самым у0(х), после чего можно будет решать Eq_1 относительно y1(x).

На заметку
Коэффициент при первой степени параметра epsilon определяется процедурой coef f (). Первым ее аргументом указана левая часть уравнения Eq (lhs(Eq)) – именно в левой части содержатся слагаемые с epsilon. Второй параметр (epsilon) является указанием на то, что нужно выделить коэффициент при первой степени epsilon. Приравняв этот коэффициент к нулю, получаем нужное уравнение.

Практически точно так же получаем последнее дифференциальное уравнение – приравниваем к нулю коэффициент при второй степени epsilon. Отличие от предыдущего случая состоит в том, что вторым параметром в процедуре coeff() указано epsilonA2.

Источник

Разложение по малому параметру

О нем не только что рассказ написать, о нем целые тома сочинений написать можно было бы.

Общая постановка задачи такова. Рассмотрим дифференциальное уравнение

с малым параметром ε. Для простоты мы будем рассматривать только задачу Коши для этого уравнения:

а частичные суммы этого ряда аппроксимируют решение сколь угодно точно. В общем случае ряд (3) вовсе не обязательно оказывается сходящимся. Его частичную сумму

Задача О30.1. Покажите, что решение задачи Коши

не может быть представлено в виде сходящегося ряда (3).

Основная задача теории возмущений — это задача о возможности построения асимптотики решений обыкновенных дифференциальных уравнений с параметром. Дифференциальные уравнения, которым удовлетворяют члены асимптотик, оказываются, как правило, существенно проще исходных уравнений, а свойство (6) асимптотических разложений позволяет эффективно исследовать поведение решений при малых ε, несмотря на то, что асимптотические ряды часто оказываются не сходящимися. В настоящее время асимптотические методы исследования решений дифференциальных уравнений успешно дополняются численными методами.

Вопрос о существовании асимптотических разложений в случае гладкой зависимости f от ε решается легко. Например, из теоремы о липшицевости оператора сдвига вытекает, что если f удовлетворяет условию Липшица по x и ε, то

где φ 0 — решение задачи при а r 1 удовлетворяет условию Липшица по ε и, следовательно, в частности,

Таким образом, в этом случае φ 0 является асимптотикой нулевого порядка решения задачи (или еще говорят о главном члене асимптотики ). о дифференцировании оператора сдвига позволяет в случае если f имеет удовлетворяющие условию Липшица производные по совокупности переменных x и ε построить асимптотику первого порядка :

В ней φ 0 та же самая, что и выше, а φ 1 — решение соответствующего уравнения в вариациях.

Точно так же теорема о существовании старших производных решения по параметру позволяет выписать и обосновать асимптотики старших порядков, выписать конечную сумму (4) ряда Тейлора и оценить остаточный член функции определяются из соответствующих уравнений в вариациях. Эти уравнения легко получаются с помощью следующей формальной процедуры. Формальный ряд (3) подставляют в уравнение (1) и начальное условие (2), формально разлагают правую часть уравнения (1) в ряд Тейлора по ε в точке и приравнивают в получившихся формальных рядах коэффициенты при одинаковых степенях ε. Получается набор обыкновенных дифференциальных уравнений для коэффициентов ряда и набор соответствующих начальных условий.

Задача О30.3. Выпишите эти уравнения и начальные условия в случае задачи Коши

Задача О30.4. Выпишите асимптотику первого порядка для следующей задачи Коши для уравнения Риккати с малым параметром

Ситуация существенно сложнее в случае так называемых сингулярно возмущенных уравнений (правильнее говорить сингулярно возмущенных задач ). Эти термины охватывают различные классы уравнений с параметрами, в которых решения зависят от параметра не регулярным образом (см., напр., очерки Дифференциальные уравнения с малым параметром при старшей производной и Принцип усреднения). Простейшим примером такого уравнения является уравнение

с малым параметром ε. Его общее решение Ce – t /ε не аналитически (сингулярно) зависит от ε в точке

Ниже мы продемонстрируем лишь некоторые особенности асимптотик сингулярно возмущенных задач на примере задачи Коши

предполагая параметр ε малым и положительным. Решение задачи имеет вид

Попытаемся представить решение (9) в виде ряда (3). Подставляя (3) в (7) и приравнивая коэффициенты при одинаковых степенях ε, получаем

Таким образом, ряд (5) сходится к функции ко второму члену в решении (9), представляющему при решение вырожденного уравнения (нулевого порядка). Отметим два тесно связанных между собой обстоятельства. Во-первых, получившаяся сумма не удовлетворяет начальному условию (8) (обратите внимание на то, что при нахождении функции φ k оно нам не потребовалось) и, во-вторых, в получившемся разложении не аппроксимируется первый член разложения (9), наличие которого вызвано «лишним» для вырожденного уравнения начальным условием (8) (см. очерк Дифференциальные уравнения с малым параметром при старшей производной). Отметим также, что первый член в решении вне малых окрестностей нуля, вне пограничного слоя, с экспоненциальной затухает. Таким образом, полученный ряд аппроксимирует решение на отрезках вида

Задача О30.5. Проверьте последнее утверждение.

Для того, чтобы построить равномерное на асимптотическое разложение заметим, что «погранслойная» часть решения задачи регулярным образом зависит от агрегата взятого как единое целое. Это наводит на мысль представить решение в виде и попытаться разложить в ряд по степеням ε функцию (имея в виду в последующем, что например, в виде

Подставляя, как и ранее, (10) в уравнение (7) и начальное условие (8) и приравнивая члены при одинаковых степенях ε (разумеется, отдельно рассматривая функции, зависящие от независимого аргумента t и независимого в данном контексте аргумента τ), получим следующее семейство уравнений

Задача О30.6. Докажите, что

Таким образом, мы построили разложение вида (10) для решения задачи (7) – (9).

Задача О30.7. Докажите, что конечные суммы построенного разложения аппроксимируют решение задачи с порядком равномерно на любом отрезке вида

У читателя не должно складываться впечатления простоты асимптотической теории сингулярно возмущенных задач. Наоборот, в настоящее время эта теория в большой мере искусство и общие подходы и методы только начинают вырисовываться. Эффективность асимптотических методов в прикладных задачах вызывает большой интерес к ним и обуславливает обилие литературы.

Литературные указания. Несмотря на большую предысторию (асимптотические разложения начали получать во времена Ньютона), асимптотическая теория возмущений в учебниках излагается редко (см., напр., [ Свешников, Федорюк]). Различные аспекты современной теории описаны в монографиях [ Митропольский, Вазов, Бутузов, Моргунов, Ломов, Розов].

Задачи. О30.8. Найдите первые три члена асимптотики при решения задачи Коши для уравнения Дуффинга

предполагая, что λ отлично от нуля.

О30.9. Найдите первые два члена асимптотики при решения задачи Коши для уравнения Ван дер Поля

О30.10. Найдите первые три члена асимптотического разложения вида (3) для 2π-периодического решения уравнения

О30.11. Пусть в уравнении

О30.13. Найдите первые члены асимптотики π-периодического решения уравнения

О30.15. Найдите первое приближение периодического решения уравнения Ван дер Поля.

О30.16. Попытайтесь выписать асимптотику вида (10) для краевой задачи

Исследуйте ее поведение при

О30.17. Найдите асимптотику вида (10) для задачи Коши

File based on translation from T E X by T T H, version 2.32.
Created 24 Mar 2000, 14:37.
Last modified 2 May 2002.

Источник