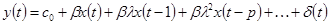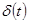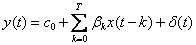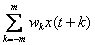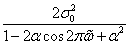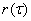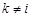разность между математическим ожиданием оценки и истинным значением оцениваемого параметра называют

Разность между математическим ожиданием оценки и истинным значением оцениваемого параметра называют

256. Разность между математическим ожиданием оценки и истинным значением оцениваемого параметра называют:
• смещением

257. Ранг наблюдения переменной — номер наблюдения переменной в упорядоченной __________________ последовательности.
• по возрастанию значений наблюдаемой величины

258. Регрессионные модели с распределенными лагами описываются соотношением
•

259. Регрессором в уравнении парной линейной регрессии называется:
• объясняющая переменная

260. Результаты проверки гипотезы H₀: b = b₀ представляются на __________________ значимости.
• двух уровнях

261. Ряд 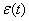, сгенерированный моделью СС (1), может быть представлен также в виде модели авторегрессии __________________ порядка.
• бесконечного

262. Свойства коэффициентов регрессии как случайных величин зависят от свойств __________________ уравнения.
• остаточного члена

263. Сглаженное значение 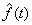вычисляется по формуле
•

264. Сглаживание временного ряда означает устранение
• случайных остатков

265. Ситуация, когда не отвергнута ложная гипотеза, называется:
• ошибкой II рода

266. Скорректированый коэффициент детерминации 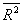с ростом числа независимых переменных
• числа испытаний

267. Случайный член n в уравнении y = ax b 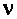задан
• мультипликативно

268. Совокупность фиктивных переменных — некоторое количество фиктивных переменных, предназначенное для описания
• набора категорий

269. Спектральная плотность 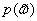марковского процесса равна:
•

270. Спектральная плотность временного ряда определяется через
• автокорреляционную функцию

Источник

Ответы на тесты по теме Экономика

Тест Фишера является:

Выборочная корреляция является __________оценкой теоретической корреляции:

Определение отдельного вклада каждой из независимых переменных в объясненную дисперсию в случае их коррелированности является ___________ задачей:

—> Условие гомоскедастичности означает, что вероятность того, что случайный член примет какое-либо конкретное значение _________ наблюдений:

одинакова для всех

Значения t-статистики для фиктивных переменных незначимо отличается от:

Остатки значений log y __________________ остатков значений y.

Если F-статистика Фишера превысит критическое значение F

, то регрессия считается:

Число степеней свободы для t-статистики равно числу наблюдений в выборке __________________ количество оцениваемых коэффициентов.

прогноз сделан успешно

Для линеаризации функции Кобба-Дугласа необходимо предварительно обе части уравнения

О наличии данной частоты в спектре временного ряда свидетельствует __________________ спектральной плотности.

При добавлении еще одной переменной в уравнение регрессии коэффициент детерминации:

—>
Стандартные отклонения коэффициентов регрессии обратно пропорциональны величине _________, где n – число наблюдений:

Зависимая переменная может быть представлена как фиктивная в случае если она:

Цель регрессионного анализа состоит в объяснении поведения

Разность между математическим ожиданием оценки и истинным значением оцениваемого параметра называют:

В авторегрессионной схеме первого порядка зависимость между последовательными случайными членами описывается формулой u

Эксперимент по методу Монте-Карло — искусственный, контролируемый эксперимент, проводимый для проверки и сравнения эффективности различных

Нижний индекс переменной (t-s) означает, что она является:

Источник

При проведении научных экспериментов невозможно проводить исследования по всей совокупности значений (генеральной совокупности), применение выборочных данных дает возможность экономии средств и затрат труда на получение и обработку информации. Объективную гарантию репрезентативности (представительности) полученной выборочной совокупности дает применение соответствующих научно обоснованных способов отбора подлежащих обследованию единиц.

Система правил отбора единиц и способов характеристики изучаемой совокупности исследуемых единиц составляет содержание выборочного метода.

Все единицы совокупности, обладающие интересующими исследователя признаками, составляют генеральную совокупность.

Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности – n.

Выборку называют репрезентативной (представительной), если она достаточно полно представляет изучаемые признаки и параметры генеральной совокупности. Для репрезентативности выборки важно обеспечить случайность отбора, с тем, чтобы все объекты генеральной совокупности имели равные вероятности попасть в выборку. Для обеспечения репрезентативности выборки применяют следующие способы отбора: простой отбор (последовательно отбирается первый, случайно попавшийся объект), типический отбор (объекты отбираются пропорционально представительству различных типов объектов в генеральной совокупности), случайный отбор – например, с помощью таблицы случайных чисел и т. п.

В эконометрике всегда известна только выборка из некоторого количества наблюдений случайной величины и по данным выборки можно рассчитать только выборочные, а не теоретические характеристики этой случайной величины

Проблема использования данных выборки для определения харак­теристик распределения может рассматриваться под разными углами зрения. Один из подходов называется оцениванием.

Пусть из генеральной совокупности извлекается выборка объемом п, причем значение признака х1 наблю­дается т1 раз, х2 т2 раз. хк наблюдается тк раз, Мы можем сопоставить каждому значению хi относительную частоту тi/п.

Статистическим распределением выборки называется перечень возможных значений признака хi и соответствующих ему частот или относитель­ных частот (частостей) mi (wi).

Числовые характеристики генеральной совокупости, как правило, неизвестные (средняя, дисперсия и др.), называются параметрами генеральной совокупности (обозначают, например, или , у2 ген). Доля единиц, обладающих тем или иным признаком в генеральной совокупности, называется генеральной долей и обозначается р.

По данным выборки рассчитывают числовые характеристики, которые называют статистиками (обозначают , или , S2, выборочная доля обозначается w). Статистики, получаемые по различным выборкам, как правило, отличаются друг от друга. Поэтому статистика, полученная из выборки, является только оценкой неизвестного параметра генеральной совокупности. Оценка параметра — определенная числовая характеристика, полученная из выборки. Когда оценка определяется одним числом, ее называют точечной оценкой.

В качестве точечных оценок параметров генераль­ной совокупности используются соответствующие выборочные характеристики. Теоретическое обосно­вание возможности использования этих выборочных оценок для суждений о характеристиках и свойствах генеральной совокупности дают закон больших чи­сел и центральная предельная теорема Ляпунова.

4.1 Несмещенные, эффективные, состоятельные оценки

До сих пор мы предполагали, что имеется точная информация о рассматриваемой случайной переменной, в частности — об ее распределении вероятностей (в случае дискретной переменной) или о функции плотности распределения (в случае непрерывной переменной). С помощью этой информации можно рассчитать теоретическое математическое ожидание, дисперсию и любые другие характеристики, в которых мы можем быть заинтересованы.

Однако на практике, за исключением искусственно простых случайных величин (таких, как число выпавших очков при бросании игральной кости), мы не знаем точного вероятностного распределения или плотности распределения вероятностей. Это означает, что неизвестны также и теоретическое математическое ожидание, и дисперсия. Мы, тем не менее, можем нуждаться в оценках этих или других теоретических характеристик генеральной совокупности.

Процедура оценивания всегда одинакова. Берется выборка из п наблюдений, и с помощью подходящей формулы рассчитывается оценка нужной характеристики. Нужно следить за терминами, делая важное различие между способом или формулой оценивания и рассчитанным по ней для данной выборки числом, являющимся значением оценки.

Поскольку оценки являются случайными переменными, их значения лишь по случайному совпадению могут в точности равняться характеристикам генеральной совокупности. Обычно будет присутствовать определенная ошибка, которая может быть большой или малой, положительной или отрицательной, в зависимости от чисто случайных составляющих величин х в выборке.

Хотя это и неизбежно, на интуитивном уровне желательно, тем не менее, чтобы оценка в среднем за достаточно длительный период была аккуратной. Выражаясь формально, мы хотели бы, чтобы математическое ожидание оценки равнялось бы соответствующей характеристике генеральной совокупности. Если это так, то оценка называется несмещенной. Если это не так, то оценка называется смещенной.

Для начала рассмотрим простейший случай, а именно когда нашей целью является применение выборки данных для оценивания средней распределения. Чтобы конкретизи­ровать задачу, предположим, что оценивается средний коэффициент умственного развития школьников. Мы получим выборку, состоящую из 5 значений коэффициента умственного развития: 90, 100, 105, 145, 100. Наша цель состоит в том, что­бы с помощью этих значений получить наилучшую оценку средней. Все возможные сведения сосредоточены в этих 5 числах. Возникает вопрос: а можем ли мы в этих условиях получить наилучшую оценку? Другими словами, какие процедуры мы должны произвести для оценивания среднего коэффициента умственного развития?

Мы получим ответ на этот вопрос, если вычислим средний коэффициент умственного развития как арифметическую среднюю всей вы­борки. Он равен 108 ( = 108). Отметим, что эта оценка является лишь приближением, полученным по данной выборке. При наличии другой выборки можно было бы получить иное приближение.

Следующий вопрос сложнее: почему мы используем в качестве оценки арифметическую среднюю, не лучше ли было бы вычислить, на­пример, среднее значение между максимальным и минимальным эле­ментами выборки? В этом случае оценка средней распределения рав­нялась бы 117,5.

Один из способов «выбора оценки» состоит в сравнении оценок, полученных на основе разных выборок из одной и той же совокуп­ности (конечно, если мы в состоянии произвести такой эксперимент). Итак, предположим, что имеется 5 различных выборок значений коэф­фициента умственного развития. Наша цель состоит в том, чтобы, ис­ходя из этих 5 выборок, оценить неизвестную среднюю распределения. В таблице 4.1 приводятся все 5 выборок и оценки их средних, вычисленные как арифметические средние значений выборки.

Среднее значение выборки ()

Предположим теперь, что мы должны ограничиться данными только первой выборки. Мы получим оценку для средней распределения, равную 108. Если бы мы имели только вторую выборку, то получили бы оценку средней, равную 107, для третьей — 113 и т. д. Средняя всех этих оценок средних равна 109, 6.

Рассмотрим, что произойдет, если мы будем увеличивать число выборок. С увеличением их числа будет расти число оценок средних и средняя этих оценок будет приближаться к истинной средней распределения. Предположим, например, что нами получено 5000 выборок; в этом случае средняя 5000 выборочных оценок средних отличалась бы от истинной средней не больше чем на 1/2 стандартного отклонения распределения.

Суммируя все вышесказанное, предположим, что средняя рас­пределения оценена и что процедура оценивания представляет собой вычисление арифметической средней по всем случайным выборкам. Выборочная оценка средней, выведенная из одной выборки, может быть близка или не близка к истинному значению средней. Однако, чем больше мы имеем оценок для разных выборок, тем ближе средняя этих оценок к истинной средней распределения. Поэтому говорят, что арифметическая средняя дает оценку средней распределения, обладающую свойством несмещенности.

Более общее определение несмещенности формулируется так: оператор оценивания параметра обладает свойством несмещенности, если средняя выборочных оценок, получаемых из независимых случайных выборок, приближается к истинному значению параметра, когда число выборок неограниченно возрастает. Это определение, конечно, не предполагает, что каждая новая оценка будет все меньше отличаться от истинного значения параметра. Однако из определения следует, что при увеличении числа выборочных оценок их средняя имеет тенденцию приближаться к истинному значению параметра.

Теперь мы вернемся к проблеме вычисления несмещенной выборочной оценки для дисперсии распределения. Рассмотрим случай, когда средняя распределения также неизвестна. Воспользуемся данными предыдущего примера. Итак, мы изучаем распределение коэффициентов умственного развития для школьников. Теоретически это означает, что мы в состоянии перечислить значения коэффициента умственного развития из их неограниченной совокупности. Тогда мы скажем, что одно из возможных значений показателя из этого распределения равно 90, другое —100, третье — 105 и т. д. Первые 15 значений распределения приводятся в первом столбце таблице 4.2.

Вариацию для каждого значения распределения мы можем полу­чить, вычитая из него величину истинной средней распределения. Предположим, что нам известна величина средней и что она равна 110 (м = 110). Разность между 15 выборочными значениями показателя и этой средней приводятся во втором столбце таблицы 4.2. Если бы мы были в состоянии вычислить аналогичные разности для всех возможных значений распределения, то сумма всех этих разностей равнялась бы нулю. Однако нас интересуют квадраты разностей, так как их средняя дает значение дисперсии. Квадраты разностей для 15 элементов рассматриваемого распределения приводятся в третьем столбце таблицы 4.2.

Таблица 4.2 – Вариации, вычисленные с помощью известной средней

Сумма квадратических отклонений для каждой выборки из пяти значений

Источник

ГЛОССАРИЙ. Эконометрика – часть экономической науки, занимающаяся разработкой и применением математических, и прежде всего экономико-статистических

Эконометрика – часть экономической науки, занимающаяся разработкой и применением математических, и прежде всего экономико-статистических, методов анализа экономических процессов, обработки статистической экономической информации.

Эконометрические методы –методы исследования экономики, изучающие экономические процессы с количественной стороны.

Выборка –некоторое количество наблюдений, отобранных из генеральной совокупности.

Наблюдение –наблюдаемое значение случайной величины или набора случайных величин.

Оценка, способ оценивания (estimator) –общее правило, формула для получения приближенного численного значения какого- либо параметра по данным выборки.

Значение оценки (estimator) –число, полученное в результате применения оценки к конкретной выборке.

Смещение – разность между математическим ожиданием оценки и истинным значением оцениваемого параметра.

Несмещенная оценка –оценка, имеющая нулевое смещение.

Эффективная оценка – несмещенная оценка, имеющая наименьшую дисперсию среди всех несмещенных оценок.

Эксперимент по методу Монте-Карло – искусственный, контролируемый эксперимент, проводимый для проверки и сравнения эффективности различных статистических методов.

Состоятельная оценка – оценка, у которой смещение и дисперсия стремятся к 0 при увеличении объема выборки.

Модель – совокупность переменных и связей между ними в форме уравнений, описывающая зависимость между наблюдаемыми переменными.

Модель парной регрессии – простейшая линейная модель зависимости между двумя переменными: .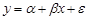

Случайный член регрессии – слагаемое и в модели 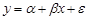, которое описывает воздействие случайных факторов.

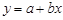
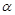
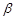
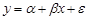
Уравнение линейной регрессии – уравнение , где a и b- оценки параметров и , полученные в результате оценивания модели регрессии по данным выборки.

Остаток в наблюдении – разность 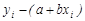между истинным значением переменной у в
i-ом наблюдении (у_i) и значением 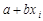i-ом наблюдении, полученным подстановкой наблюдения х_i в уравнение линейной регрессии.

Метод наименьших квадратов (МНК) (OLS – Ordinary Least Squares) – метод нахождения оценок параметров регрессии, основанный на минимизации суммы квадратов остатков всех наблюдений.

Объясненная дисперсия зависимой переменной – выборочная дисперсия расчетных значений величины y: .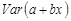

Необъясненная дисперсия зависимой переменной – выборочная дисперсия остатков в наблюдениях: .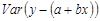

Общая сумма квадратов отклонений (TSS – Total Sum of Squares) – сумма квадратов отклонений величины у от своего выборочного среднего .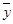

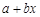
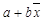
Объясненная сумма квадратов отклонений (ESS – Explained Sum of Squares) – сумма квадратов отклонений величины от своего выборочного среднего .

Необъясненная (остаточная) сумма квадратов отклонений (RSS – Unexplained Sum of Squares) – сумма квадратов остатков всех наблюдений.

Коэффициент детерминации R 2 – доля объясненной дисперсии зависимой переменной во всей выборочной дисперсии у: .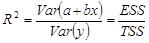

Стандартное отклонение случайной величины – корень квадратный из теоретической дисперсии случайной величины; среднее ожидаемое расстояние между наблюдениями этой случайной величины и ее математическим ожиданием.

Стандартная ошибка случайной величины – оценка стандартного отклонения случайной величины, полученная по данным выборки..

Нулевая гипотеза (Н_о) – утверждение о том, что неизвестный параметр модели принадлежит заданному множеству А.

Альтернативная гипотеза – утверждение о том, что неизвестный параметр модели принадлежит другому заданному множеству В, .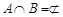

Область принятия гипотезы – множество значений оценок параметра, при попадании в которое нулевая гипотеза не отвергается.

Ошибка I рода – ситуация, когда оценка параметра не попала в область принятия нулевой гипотезы, нулевая гипотеза была отвергнута, хотя та была истинной.

Ошибка II рода – ситуация, когда не отвергнута ложная гипотеза.

Цена ошибки – численное выражение ущерба от ошибки, величина «штрафа» за ошибку.

Функция цены – функция, где аргументом является род ошибки, а значением функции – цена ошибки..

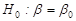
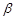
Т-тест (тест Стьюдента) – проверка гипотезы о значении коэффициента с помощью распределения Стьюдента.

Число степеней свободы – натуральное число, характеристика таких законов распределения, как распределение Стьюдента, распределение Фишера и некоторых других.

Критическое значение теста при р-процентном уровне значимости – граничное значение области принятия гипотезы, проверяемой тестом, p-процентной вероятностью совершить ошибку I рода.

Доверительный интервал – интервал с центром в полученной оценке параметра, который содержит истинное значение параметра с доверительной вероятностью.

Односторонний тест – тест на проверку гипотезы, в котором область принятия гипотезы имеет только одно критическое значение.

F-тест (тест Фишера)‘ – проверка гипотезы 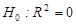(значимость всей регрессии) с помощью распределения Фишера.

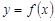
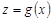
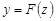
Нелинейная по переменным модель – нелинейная модель , в которой возможна замена переменной , приводящая получившуюся модель – к линейной.

Нелинейная по параметрам модель – модель, которую нельзя привести заменами переменных к линейной.

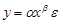
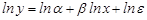
Логарифмическое преобразование – переход от нелинейной и по переменным, и по параметрам модели к логарифмической модели .

Метод Зарембки – процедура выбора между линейной и логарифмической моделями.

Тест Бокса-Кокса (решетчатый поиск) – прямой компьютерный метод выбора наилучших значений параметров нелинейной модели в заданных исследователем пределах с заданным шагом (решеткой).

Итерационные методы – компьютерные сходящиеся методы поиска наилучших значений параметров нелинейной модели.

Модель множественной регрессии – линейная модель зависимости между переменными: 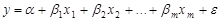, содержащая более двух переменных

Модель множественной регрессии без свободного коэффициента – линейная модель зависимости между переменными: 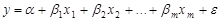, не содержащая коэффициента

Плоскость регрессии – m-мерная плоскость 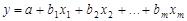в (т + 1)-мерном пространстве

Нестрогая линейная зависимость между переменными – ситуация, когда теоретическая корреляция двух переменных близка к 1 или –1

Строгая линейная зависимость между переменными – ситуация, когда выборочная корреляция двух переменных равна 1 или –1

Мультиколлинеарность – явление, когда нестрогая линейная зависимость между объясняющими переменными в модели множественной регрессии приводит к получению ненадежных оценок регрессии

Полная коллинеарность – явление, когда строгая линейная зависимость между переменными приводит к невозможности применения МНК

Лишняя переменная – объясняющая переменная, включенная ‘в модель множественной регрессии, в то время, как по экономическим причинам ее присутствие в модели не нужно

Отсутствующая переменная – необходимая по экономическим причинам объясняющая переменная, отсутствующая в модели

Спецификация переменных – выбор необходимых для регрессии переменных и отбрасывание лишних переменных

Замещающая переменная – объясняющая переменная, используемая в регрессии вместо трудноизмеримой, но важной переменной

Лаговая переменная – наблюдение зависимой переменной регрессии в предшествующий момент, используемое как объясняющая переменная

Фиктивная переменная – переменная, принимающая в каждом наблюдении только два значения: 1 – «да» или 0 – «нет»

Набор категорий – конечный набор взаимоисключающих событий, полностью исчерпывающий все возможности

Совокупность фиктивных переменных – некоторое количество фиктивных переменных, предназначенное для описания набора категорий

Эталонная категория – категория, с которой сравниваются другие категории

Сезонные фиктивные переменные – совокупность фиктивных переменных, предназначенная для обозначения различных лет, времен года, месяцев и т.п.

Ловушка dummy trap – выбор такой совокупности фиктивных переменных, у которой сумма этих переменных тождественно равна константе

Фиктивная переменная взаимодействия – фиктивная переменная, предназначенная для установления влияния на регрессию одновременного наступления сразу нескольких независимых друг от друга событий, каждое из которых описывается своей фиктивной переменной

Гетероскедастичность – нарушение второго условия теоремы Гаусса-Маркова, которое заключается в том, что дисперсия случайного члена регрессии зависит от номера наблюдения: 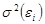– зависит от i

Ранг наблюдения переменной – номер наблюдения переменной в упорядоченной по возрастанию последовательности

Тест ранговой корреляции Спирмена – тест на гетероскедастичность, устанавливающий, что стандартное отклонение остаточного члена регрессии имеет нестрогую линейную зависимость с объясняющей переменной

Тест Голдфелда-Квандта – тест на гетероскедастичность, устанавливающий, что стандартное отклонение остаточного члена регрессии растет, когда растет объясняющая переменная

Тест Глейзера – наиболее тонкий тест на гетероскедастичность, улавливающий нелинейную связь между стандартным отклонением остаточного члена регрессии и объясняющей переменной

Автокорреляция (случайного члена в уравнении регрессии) – нарушение третьего условия Гаусса-Маркова, которое заключается в том, что случайные члены регрессии в разных наблюдениях являются зависимыми: 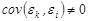, при

Положительная автокорреляция (случайного члена) – ситуация, когда случайный член регрессии в следующем наблюдении ожидается того же знака, что и случайный член в настоящем наблюдении

Отрицательная автокорреляция (случайного члена) – ситуация, когда случайный член регрессии в следующем наблюдении ожидается знака, противоположного знаку случайного члена в настоящем наблюдении

Автокорреляция первого порядка – ситуация, когда коррелируют случайные члены регрессии в последовательных наблюдениях

Критерий Дарбина-Уотсона – метод обнаружения автокорреляции первого порядка с помощью статистики Дарбина-Уотсона

Зона неопределенности критерия Дарбина-Уотсона – промежуток значений статистики Дарбина-Уотсона, при попадании в который критерий не дает определенного ответа о наличии или отсутствии автокорреляции первого порядка

Поправка Прайса-Уинстена – метод спасения первого наблюдения в автокорреляционной схеме первого порядка

Метод Кокрана-Оркатта – компьютерный итерационный метод устранения автокорреляции первого порядка.

Панельные данные –данные нескольких одновременных временных рядов

Временной ряд (time series) –наблюдения экономического показателя одного объекта в равноотстоящие моменты времени

Член временного ряда –наблюдение экономического показателя одного объекта в некоторый момент времени

Перекрестные данные (cross-section data) –выборка из экономических показателей, полученная для большого количества однотипных объектов (семей, фирм, регионов, стран); все наблюдения или одновременные, или считаются независимыми от времени

Долговременные факторы –неслучайные факторы, формирующие тенденцию

Тренд –тенденция, которую формируют долговременные факторы

Сезонные факторы –факторы, обусловленные периодичностью (сезонной, квартальной)

Циклические (конъюнктурные) факторы –факторы, обусловленные действием долгосрочных циклов (солнечная активность, демографические «ямы», волны Кондратьева, политические выборы)

Случайные факторы –факторы, не поддающиеся учету и регистрации

Разладочные случайные факторы –случайные факторы, приводящие к резкому изменению (слому) всей модели

Эволюционные остаточные случайные факторы –случайные факторы, влияние которых не приводит к резкому изменению ни характера, ни параметров модели

Строго стационарный (стационарный в узком смысле) временной ряд –временной ряд х(t), у которого совместное распределение вероятностей тнаблюдений х(t₁), х(t₂), …,х(t_m) такое же, как и для m наблюдений х(t₁+t), х(t₂+t), …,х(t_m+t) для любого т, t₁, t₂, t_m и t.

Стационарный (стационарный в широком смысле) временной ряд – Временной ряд х(t) с постоянным математическим ожиданием М(х(t)) и дисперсией D(х(t)), не зависящими от t

Нестационарный временной ряд – Временной ряд отличающийся от стационарного на неслучайную составляющую (тренд)

Автоковариационная функция – функция 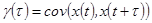для стационарного ряда (зависит только от t)

Автокорреляционная функция – функция 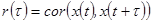для стационарного ряда (зависит только от t)

Коррелограмма – график автокорреляционной функции

Частная (очищенная) автокорреляционная функция – функция, измеряющая корреляцию х(t) и х(t+t) напрямую, без влияния промежуточных между ними наблюдений

Спектральная плотность временного ряда – сумма ряда 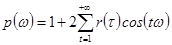, где r(t) – автокорреляционная функция.

Серия – Последовательность подряд идущих плюсов или минусов

Критерий серий – критерий, основанный на исследовании количества серий и их длин в последовательности

Метод скользящего среднего – метод сглаживания временного ряда для уменьшения влияния случайных факторов

Метод последовательных разностей – метод поиска степени многочлена, описывающего тренд

Белый шум – временной ряд 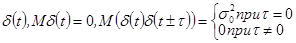, серия импульсов, генерирующая случайные остатки анализируемого временного ряда.

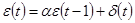
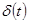
Модель авторегрессии 1-го порядка АР(1), марковский процесс (АR(1) models) –временной ряд, описываемый формулой ,-где – белый шум

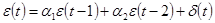
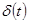
Модель авторегрессии 2-го порядка АР(2), модель Юла (АR(2) – models) –временной ряд, описываемый формулой , где – белый шум

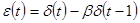
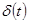
Модель скользящего среднего 1-го порядка СС(1) (MA(1) models) –временной ряд, описываемый формулой , где –белый шум

Условия стационарности –условия на параметры модели, при которых временной ряд получается стационарным

Условия обратимости –условия на параметры модели, при которых зависимость значения временного ряда от прошлых значений уменьшается с отдалением прошлого

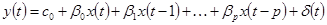
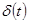
Регрессионная модель с распределенными лагами –модель зависимости , где – белый шум

Лаговая структура Ш. Алмон –Регрессионная модель с распределенными лагами, в которой параметры получаются по формуле 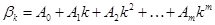, где A₀, A₁, A₂,…A_m –неизвестные параметры

Лаговая структура Койка –Регрессионная модель с распределенными лагами, в которой параметры убывают в геометрической прогрессии: ,где – белый шум, –1

Источник