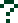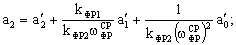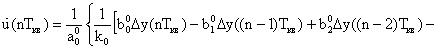регулятор с переменными параметрами
ПИД-регуляторы – для чайников-практиков
Обещал я недавно моему знакомому — хорошему электрику и чайнику в электронике — сделать небольшое устройство в автомобиль, которое, регулируя заслонку, будет поддерживать обороты в дОлжном состоянии (все подробности по авто-части к нему. Знаю, что назвали мы эту чучу умным словом «регулятор холостого хода»). Причем эти обороты должны зависеть от текущей температуры двигателя. «Так тебе нужно работать с ПИД-регулятором» — сказал я ему. А в ответ увидел туман в глазах, дым в ушах и дрожащий голос – «А это ничего общего со СПИДом не имеет. ». В общем, придется ему объяснить подробности, при этом избегая математики. В Интернете море статей на эту тему (достаточно начать отсюда). Моя статья – еще одна ложка в море информации. Интересующимся – под кат!
Что мы делаем?
Итак, мы делаем регулятор холостого хода.
В данном случае однозначно просится к реализации система управления с обратной связью. В своей статье про «Датчики и АЦП» я рассказывал про систему управления с обратной связью, подробности ищите там. Также там была неплохая картинка на эту тему:
Что это будет в данном случае?
Мы хотим управлять оборотами двигателя в состоянии холостого хода. Для этого у нас есть шаговый двигатель, который открывает/закрывает заслонку для регулировки подачи воздуха. Также у нас есть таблица, которая указывает желаемую частоту двигателя в зависимости от текущей температуры. Управление объектом тут у нас выполняется шаговым двигателем. Состояние объекта определяется 1) оборотами двигателя и 2) текущей температурой.
Для данной картинки получаем следующее:
Что это за функция? Она выдает нам текущее значение шага, которое зависит от всего вышеперечисленного. Как она это делает?
Вся собака зарылась в том, что мы хотели на данный шаг получить одни обороты, а они в реальности совсем другие! Значит, нам нужно знать значение текущей ошибки (невязки), и она может быть вычислена как разность предполагаемых оборотов в будущем и текущих:
Ошибка (t) = Обороты (t+1) — Обороты (t).
В случае, когда обороты четко соответствуют требуемому значению (к чему мы и стремимся), ошибка будет равна нулю. Эта ошибка нам показывает насколько сильным должно быть воздействие.
Формула для следующего шага теперь может быть записана следующим образом:
Теперь можно вынести значение предыдущего шага за скобки:
Все понятно? Мы на каждом шаге работы регулятора должны задавать текущее положение шагового двигателя. Он зависит, понятное дело, от предыдущего шага и от ошибки. Шаговый двигатель управляется смещениями, поэтому нам не так уж и важен текущий шаг (проигнорируем тему выхода за пределы допустимого количества шагов – моему другу электрику это знать не обязательно). В итоге можно перейти к такой записи:
Формула ПИД-регулятора
Как я и обещал, формул тут не будет… ну, почти не будет. И этот раздел – как раз и будет формулой. Обещаю – больше формул не будет! Так что потерпите!
Итак, формула ПИД-регулятора: 
(навеяно Википедией)
Тут у нас следующие буковки (разъясним чуть ниже):
Вот это уже выглядит куда реальнее и понятнее! Мы вычисляем сумму трех составляющих. Каждая из них определяется своими коэффициентами. Если данный коэффициент нулевой, то составляющая в вычислении не участвует. С этой формулой мы и будем работать далее, ее я и реализую.
Впрочем, есть еще и другая, рекуррентная реализация:
Какая из них лучше/правильней? Математика, в общем-то, одинаковая. Коэффициенты тоже. Говорят, что есть разные подводные булыжники при реализации.
Обратите внимание! Коэффициенты тут – обязательно дробные числа! В языке программирования Си – как минимум float, а лучше бы и double.
Вся магия ПИД-регуляторов – именно в этих коэффициентах. Как их подбирать – посмотрим в конце. А сейчас переведем дух от математики и поедем к изучению поведения этой формулы.
Все расчеты и моделирование я проводил на модели в Excel. Он – файл – приложен внизу, с ним можно поиграться самостоятельно. Модель – сугубо для ознакомления с идеей! Т. е. не надо ее стараться привести к какому-то реальному процессу, искать в ней научный смысл и т. п. Там все цифры слегка «отфонарные». Но зато и файл простенький и несложный. И моделируется быстро. И дает возможность понять суть ПИД-регулятора. Пару слов по файлу я дам в конце.
Пропорциональная составляющая
Первый коэффициент – пропорциональный. Он самый очевидный и понятный (реально я когда-то давно сам вывел формулу ПИД-регулятора, кому-то показал, и он рассказал мне об этой теории; так вот, вывод я начал с пропорционального вида).
Рассмотрим его – пропорционального коэффициента — влияние на результат.
«Ожидаемое» – это то, что мы хотим получить. Вначале оно равно какому-то низкому значению (в нашем примере – это те обороты двигателя, которые создает стартер). Далее, в момент времени 3, оно вдруг стало равно 2000 (завели мотор и, исходя из текущей температуры, мы должны получить 2000 оборотов в минуту).
(Небольшая ремарка – в автомобилях частоту измеряют в кол-во оборотов в минуту!)
Сделаем первый вариант: Kp = 2. Посмотрим на красную линию. Что мы видим? По ходу дела обороты начали расти – ошибка стала снижаться – значение коррекции постепенно растет — красная линия растет (обороты двигателя увеличиваются). В какой-то момент (почему-то 13-ый) обороты достигают требуемой величины. Класс? Супер! Да вот только медленно как-то…
Попробуем другой коэффициент: Kp = 5. Что видим? Зеленая линия. Достигла результата шустро – на 6-ом шаге. Класс! Да вот – ой! – перелет (по науке перерегулирование). Потом, правда, вернулись назад – порядок.
А что если коэффициент сделать еще больше? Kp = 20. Синяя линия – бух! За один шаг! Но – сразу перелет. Потом падаем вниз – ошибка стала отрицательной. Опять сильно вниз! Рывок вверх! Опять вниз! Что видим? Пошли колебания. Они, слава Богу, затухающие.
Если увеличивать коэффициент больше, то такие колебания могут стать незатухающими. Система начнет колебаться все больше и больше, пока не … ну-у, тут уже все зависит от конкретной системы.
Какова природа колебаний? Система, на которую воздействуют, всегда (в реальной жизни) инерционна. Обороты повышаются – коэффициент падает к нулю. И вот – достигли нужной точки. Коэффициент ошибки (и регулирования) достиг нуля. Но ведь процесс поднятия оборотов инерционен! Движёк раскочегарен, обороты продолжают по инерции расти. И тогда будем двигать заслону назад – опускать обороты. Опять достигли нуля – а обороты продолжают падать… И так, в общем-то, до бесконечности.
Особенно это очевидно в системах поддержания температуры. Нагрев надо выключать до нужной температуры – чтобы сам нагреватель перестал разогреваться и греть объект.
Для решения этой проблемы используется следующая –
Интегральная составляющая
Эта составляющая накапливает ошибку (как и любой интегратор). Т. е. постепенно накапливается эта самая ошибка, интегратор «наполняется» и его воздействие увеличивается. Эффект от такого накопления не мгновенен — ибо ошибка должна накопиться, на что уходит некоторое количество шагов алгоритма.
Рассмотрим случай, когда Kp = 5, а Ki будем менять: 
Дифференциальная составляющая
Реакция на помехи
Надо еще не забывать об одной такой малоприятной вещи – о помехах. Они будут раскачивать лодку нашей системы.
Вот картинка, когда у нас стоит задача поддерживать одно и то же значение оборотов: 
Шумовое (случайное) воздействие – одинаковое для всех вариантов.
Вариант 1 (красный) – Kp = 10, Ki = 0, Kd = 10.
Вариант 2 (зеленый) – Kp = 10, Ki = 2, Kd = 0.
Вариант 3 (синий) – Kp = 10, Ki = 2, Kd = 6.
Как видно, с добавлением составляющих стабильность (немного) увеличивается.
Настройка
Я думаю, общее представление о формуле ПИД-регулирования вы получили. Программируется легко, эффект красивый. И следующий вопрос у вас будет – «а как получит коэффициенты»? И вот тут все становится кисло… Потому что, если до этих пор шла строгая математика, то дальше начинаются танцы с бубнами, шаманство и шайтанство. Нет, все-таки есть какие-то точные методы, но мне становится плохо при мысли, что я должен это проделать для своего двигателя в автомобиле!
В комментариях мой метод (и мое понимание) настройки разгромили, закопали и затоптали. И порекомендовали прочитать хорошую книгу «ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ДЛЯ «ЧАЙНИКОВ»» К.Ю. Полякова (созвучное название, не находите?). Согласен, тема (настройки) сложная, для меня неоднозначная, поэтому соглашусь с комментирующими — надо прочитать эту книгу и глубже вникать в тему. Но… это уже будет не для уровня чайников, не так ли? В книге Полякова формул более чем достаточно, а это уже уровень электро-чайника! Так что позвольте мне изложить свой подход. Неидеальный, но достаточный для старта и более детального изучения темы.
Частота опроса/воздействия
Есть очень важный момент работы при разработке ПИД-регулятора: воздействие должно быть строго периодичным, т. е. производиться через равные промежутки времени! Аналогично, ошибка должна вычисляться также периодически.
Какой должен быть период измерений/воздействий? Для начала определите время стабилизации системы – за сколько должно быть достигнуто устойчивое состояние (в случае регулятора холостого хода хватит периода 0.5 секунды). Потом разделите это время на 10 … 100 – и вы получите длительность шага (в моем случае хватит и 10 мсек). А вообще – чем выше частота, тем лучше! Но надо помнить, что операции с дробными числами весьма медленны. Фактически, они и зададут вам период работы.
Посмотрим, как период опроса (и воздействия) влияет на качество результата:
Коэффициенты ПИД-регулятора: – Kp = 10, Ki = 0, Kd = 0.
Вариант 1 (красный) – период опроса 0.5 у.е.
Вариант 2 (зеленый) – период опроса 0.35 у.е.
Вариант 3 (синий) – период опроса 0.15 у.е.
Как видим, в первом случае есть мощные выбросы. Во втором случае (70% от первого периода) они стали слабее, а в третьем (30%) – преобразование вообще получилось гладким! Т. е. для первых двух вариантов нужны дополнительно интегральная или дифференциальная составляющие, а для последнего мы обошлись только пропорциональной. А это существенная разница в вычислениях!
Так что вопросу выбора периода надо уделить первостепенное внимание.
Итак, время выбрали, все коэффициенты сбросили в ноль. Начинаем управлять системой.
Идеально, если вы сможете собрать статистику – записывать воздействие/результат/сопутствующую информацию в текстовый файл. Потом его можно открыть в том же Excel и проанализировать.
Настройка пропорционального коэффициента Kp
Для начала я устанавливаю коэффициент Kp в 1 и смотрю, что будет. Растет слишком медленно – увеличиваю. В какой-то момент начнутся перелеты и колебания. Значит, многовато – уменьшаем. Исчезли – немного увеличиваем. Начались – немного уменьшаем. Исчезли — … И так далее, пока не надоест. В итоге получили достаточно устойчивый пропорциональный регулятор, который надо немного скорректировать (надо ли? Если все работает вполне качественно, то не морочим себе голову и считаем, что все настроено)
Настройка дифференциального коэффициента Kd
Понемногу наращиваю коэффициент Kd — 0.5, 1,… Колебания системы уменьшаются, все работает красивее… Пока не происходит обратное – начинаются мощные выбросы. Все, перерегулировали, уменьшаем.
Итак, имеем выбросы – уже меньше, но все равно имеем. Самое то сгладить, притормозить воздействие!
Настройка интегрально го коэффициента Ki
Шаманим дальше. Берем совсем немного – 0.1 для начала. Можно попробовать и небольшое отрицательное значение. Смотрим, пробуем, крутим…
Процесс этот – настройки – итерационный. Стоит пробовать разные варианты, начинать сначала. Для меня он по-прежнему туманен и шайтанен.
Дополнительные модули?
Построили, сделали — и увидели, что все равно есть какие-то биения, ненужные колебания. Ну-с, а что вы хотели. Серьезный подход изобилует формулами, сложными расчетами!
И Бог с ними — вот что я скажу! Можно вполне на выходе добавить усреднение нескольких последних тактов — дешево (в плане расчетов) и сердито (в плане стабильности воздействий). Можно поставить еще какие-нибудь фильтры.
Не будем догматичными! Кто сказал, что нужно ограничиться одним лишь ПИД-регулятором?
Информация по модели
А теперь – обещанная пара слов по Excel-файлу. В нем реализована модель, схожая с перемещением по линии. Не очень корректная, возможно, но вполне достаточная для старта (может, по результатам обсуждения сделаю более точную модель — возьму для примера модель электродвигателя из статьи Полякова). Есть предыдущее положение, скорость и ускорение. Скорость рассчитывается как разница предыдущих перемещений. Ускорение определяется как П-И-Д – воздействие, умноженное на коэффициент усиления (в верхней части таблицы).
В таблице представлены 3 варианта. Они настраиваются сверху:
В заключение – о реализации
Как видите – ничего революционного!
Прежде всего, все радости происходят в отдельной функции, которая вызывается периодически.
Первый вызов – инициализация из EEPROM или откуда-нибудь еще коэффициенты, обнуляем переменные для рекурсивных вызовов. Потом начинаем пошагово 1) измерять, 2) вычислять, 3) воздействовать, и так по кругу. Заодно производится привязка к реальному времени. Если текущее время меньше требуемого (функция TimeIsLower), то действие не производится.
В комментариях поинтересовались — зачем такие сложности с машиной состояний? С недетерминированным алгоритмом? Отвечаю: благодаря такому подходу я реализую простенький «параллелизм». Т. е. в промежутке между этапами вычислений я делаю какие-то другие действия (в моем случае общение по UART, которое может быть весьма напряженным — когда я использую сий девайс как логгер событий).
Вроде бы все… Что забыл, что перепутал – пишите. Как всегда, приветствуются комментарии о ляпах и ошибках!
P. S.Хочу поучаствовать в конкурсе, поэтому добавляю: 
Автоматика.
Автоматизация.
Электротехнические
комплексы и системы.
РЕГУЛЯТОР ПЕРЕМЕННОЙ СТРУКТУРЫ ДЛЯ
ОБЪЕКТОВ ТЕХНОЛОГИЧЕСКОГО ТИПА
Хобин В.А.
В условиях возрастания требований к точности соблюдения режимными переменными объектов управления (ОУ) установленных регламентов и роста потерь при их нарушениях, задача совершенствования алгоритмов регулирования сохраняет свою актуальность и остается в числе традиционных задач теории автоматического управления. Вместе с тем, как показывает практика, когда в качестве объектов управления выступают технологические агрегаты (процессы) (ТА ТП), то разработчики систем автоматического регулирования (САР), в подавляющем большинстве случаев используют простейшие ПИ-, ПИД-алгоритмы регулирования. Это обстоятельство может быть объяснено следующими двумя взаимообусловленными факторами.
Во-первых, ТА как ОУ имеют специфические особенности по сравнению с такими объектами, как манипуляторы, электропривод, усилители, транспортные (мобильные) средства. Основные из них: а) физическая распределенность каналов управления ТА, проявляющаяся в значительных запаздываниях реакции управляемых переменных на управляющие воздействия; б) большое количество факторов весьма существенно влияющих на работу ТА, но практически недоступных для измерения (характеристики сырьевых и энергетических потоков, состояние рабочих органов и активных зон ТА), проявляющихся как неконтролируемые возмущения (координатные, параметрические), и изменяющие значения управляемых переменных, свойства каналов управления, оптимальные режимы работы ТА; в) критерий (функционал) оптимальности управления не включает в себя составляющих, штрафующих скорости изменения управляющих воздействий, т.е. он не имеет вида критерия «обобщенной работы». Эти особенности ОУ технологического типа делают совершенно неоправданными как «копирование» самих алгоритмов регулирования, разработанных для других типов объектов, так и методов разработки этих алгоритмов.
Во-вторых, для ПИД-регуляторов, используемых в САР, для объектов технологического типа имеется инфраструктура инженерной поддержки их применения. Она включает в себя типовые модели динамики каналов регулирования, упрощенные процедуры параметрической идентификации этих типовых моделей, типовые методики расчета настроечных параметров регуляторов или их начальных приближений, типовые аппаратные и программные средства, реализующие эти алгоритмы [1]. Эта инфраструктура сложилась, эволюционируя в ходе практического применения всех ее компонентов. Это гарантирует работоспособность разработанных типовых САР на этапе их внедрения.
ПИД-алгоритм регулирования (регулятор) можно рассматривать как базовый для построения САР объектами технологического типа. То есть такой регулятор, который: а) представляет собой целостный алгоритмический модуль, который может использоваться как регулятор локальной САР технологическим контуром, или в качестве составляющей более сложного алгоритма; б) имеющий фиксированную (закрытую для изменений) структуру, и позволяющий пользователю производить только его параметрическую настройку; в) сопровождаемый инженерными методиками квазиоптимальной настройки; г) имеющий техническую поддержку в форме доступного для применения аппаратного и (или) программного обеспечения, реализующего алгоритм.
Очевидно, что сколько-нибудь широкое применение вместо базового ПИД- алгоритма, новых, более эффективных алгоритмов, возможно только тогда, когда они смогут претендовать на роль базовых.
Сформулируем основные требования, которым должен отвечать регулятор, претендующий стать альтернативой ПИД-регулятору [2, 3]: а) эффективная (т.е. с высокой динамической точностью и низкой интенсивностью случайных выбросов этой переменной за установленный уровень) стабилизация регулируемых переменных ОУ в окрестности заданного значения; б) быстрый и без значительных перерегулирований перевод регулируемых переменных от значений, которые отвечают режиму холостого хода ОУ, к их значениям, которые отвечают номинальному режиму; в) сохранение перечисленных выше свойств САР при значительных вариациях характеристик ОУ и внешних действий, в том числе при их значительной априорной неопределенности (робастность); г) простота настройки алгоритма для пользователя, в частности его перенастройки при использовании в составе адаптивных САР.
Разработку таких алгоритмов необходимо вести отказавшись от формальных (аналитических) методов синтеза, в частности использующих методы аналитического конструирования регуляторов [4]. Это обусловлено тем, что для нестационарных нелинейных систем с запаздыванием в замкнутом контуре, получить выражение в явном виде аналитического решения системы уравнений, описывающее САР без специальных упрощений, в том числе – статистической линеаризации нелинейности, разложения трансцендентных передаточных функций запаздывания в ряд Паде и т.д., невозможно. Но и с этими упрощениями полученные выражения весьма сложны, что делает их непосредственный анализ практически невозможным.
Конструктивным для объектов технологического типа является эвристический подход, основанный на опыте, накопленном разработчиками САР, углубленных исследованиях уже апробированных на практике алгоритмов, их совершенствования, объединения в целостные альтернативные варианты алгоритмов с последующей их параметрической оптимизацией и сравнительными исследованиями в различных условиях в ходе специально организованных машинных экспериментов. В качестве таких алгоритмов использовались: а) базовый ПИД-алгоритм регулирования; б) алгоритмы коммутации структуры регулятора, в частности коммутации его настроечных параметров; в) алгоритмы прогнозирования свободного движения САР в замкнутом контуре на время запаздывания вперед; г) алгоритмы «безударного» замыкания и размыкания контура регулирования. В соответствии с таким подходом, после предшествующих исследований структура регулятора (алгоритма регулирования), как претендующего на альтернативу ПИД-регулятору, изображена на рис. 1.
Отметим, что системы с переменной структурой возникли как средство эффективного управления движением мобильными объектами по заданной траектории [5]. Эффективность обеспечивало специфическое свойство скользящих режимов, при которых достигался высокий уровень инвариантности траектории движения относительно параметров объекта. Попытки использовать это свойство при управлении технологическими объектами, включая разработку и производство специальных регуляторов [6] успеха не имели. Причина этого, как уже отмечалось – принципиальное отличие свойств мобильных и технологических объектов, как ОУ и сред (условий), в которых они функционируют, близость наиболее эффективных режимов работы объекта к предельно-допустимым, нарушения которых приводит к возникновению аварийных ситуаций. Вместе с тем идея коммутации структуры регулятора может быть достаточно плодотворна вне зависимости от реализации скользящих режимов.
Рис. 1 Структурная схема базового регулятора переменной структуры (РПС)
Модули РПС описываются следующими системами уравнений.
1. Модуль задания (МЗД):
(1)
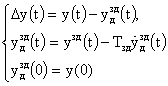
где y(t) – регулированная переменная;
узд(t),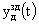 
— соответственно заданное значение регулированной переменной и ее «динамическое значение» с ограниченной скоростью нарастания;
2. Модуль динамической зоны нечувствительности (МДЗН):
(2)
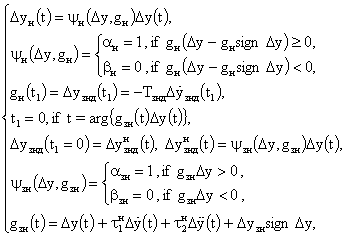
Dузнд(t),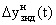 
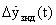
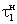
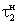
, Dузн, 
— текущее, начальное и минимальное значения зоны нечувствительности, скорость изменения Dузнд(t);
, 
— настроечные параметры gзн(t);
3. Модуль основной алгоритмический (МОА):
(3)
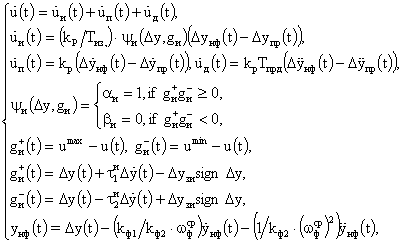
где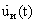 
, 
, 
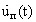
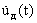
— скорости изменения соответственно интегрирующей, пропорциональной и дифференцирующей составляющих u(t);
Dу(t),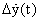 
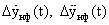
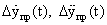
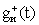
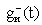
— ошибка регулирования и скорость ее изменения;
, 
— соответственно скорость и ускорение изменения переменных Dунф(t) и Dупр(t);
, 
— функции переключения yи;
4. Модуль прогнозирования движения ОУ под воздействием управления (МПР):
(4)
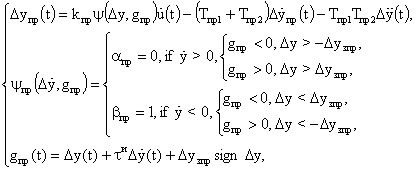
5. Модуль формирования управляющих воздействий (МФУВ):
(5)
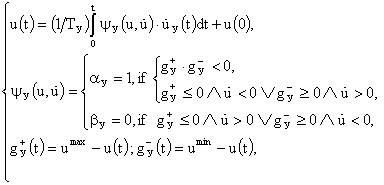
где u(t),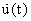 
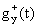
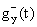
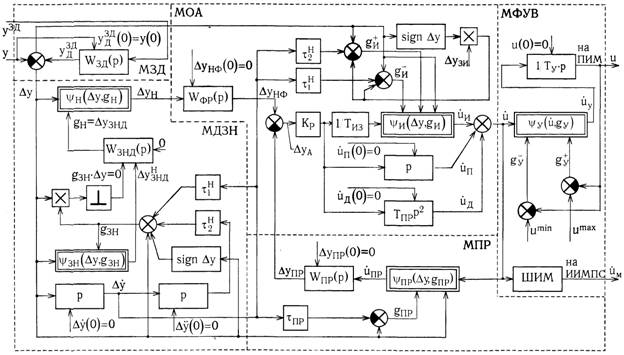
— управляющее воздействие РПС и скорость его изменения;
, 
— функции переключения yУ;
Характеристики y-ячеек представлен на рис. 2. В том случае, если все y-ячейки реализуют свои a-структуры, то РПС вырождается в обычный линейный ПИД-регулятор.
Рис. 2 Характеристики y-ячеек базового РПС
Как и для типовых линейных регуляторов, для рассматриваемого РПС- регулятора, разработаны упрощенные методики настройки параметров САР простейшей структуры, не требующие применения оптимизационных процедур. Для их применения свойства объекта управления по каналу регулирования традиционно представляются в виде модели первого порядка с запаздыванием (параметры k0, t0, Т0). Отличие методики состоит в том, что она предлагает более обоснованный выбор трех вариантов критериев САР, которым будут соответствовать настройки. Это критерии минимумов интегральных квадратичных ошибок регулирования при воздействиях на систему по каналам возмущения и запаздывания: min jf и min jy (соответственно для вариантов, когда САР преимущественно работает в режимах стабилизации и слежения), и критерий минимума средней интенсивности (частоты) нарушения регулируемой переменной установленного регламентом ограничения: min ns. Настройки, соответствующие последнему критерию ориентированы, прежде всего, на применение РПС в составе систем гарантирующего управления [7]. Номограммы и формулы для расчета параметров приведены на рис. 3.
Реализация РПС предполагает цифровой вариант. Он, с одной стороны, резко упрощает реализацию, по сравнению с аналоговым, но приводит к появлению дополнительной проблемы. Она связана с устойчивостью реализуемой РПС вычислительной процедуры. Прямое программирование алгоритма регулирования по блокам (модулям) структурной схемы регулятора (рис. 1) недопустимо из-за наличия в нем внутреннего контура прогнозирующей обратной связи. Цифровая реализация приведет к появлению в контуре дополнительного запаздывания (опережения) на шаг квантования Ткв относительно прямой цепи. А это при определенных соотношениях настроечных параметров элементов, входящих в этот контур, может привести к его неустойчивости.
Во избежание этого модули алгоритмический, прогнозирования и фильтрации описываются как единый модуль. Его передаточная функция при фиксированных структурах имеет вид:
, (6)
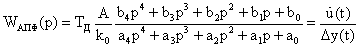
где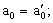 
; 
; 
;
; 
; 
;
; 
; 
;
; 
;
; 
; 
.
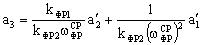
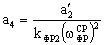
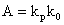
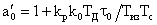
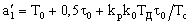
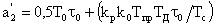
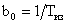
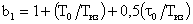
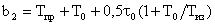
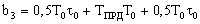
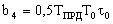
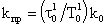
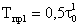
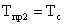
Важно, что порядок числителя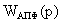 
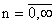
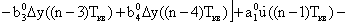
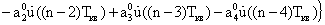
не превышает порядка знаменателя. После перехода к дискретному времени (t ® nTкв, 
), получаем:
(7)
,
где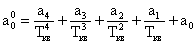 
; 
;
; 
; 
;
; 
;
; 
; 
.
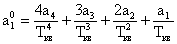
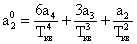
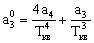
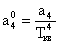
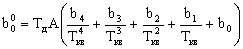
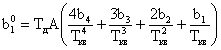
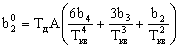
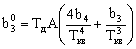
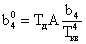
Выражение для расчета ошибки регулирования Dу при инерционном задатчике имеет вид:
. (8)
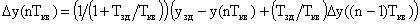
Для реализации управляющего воздействия, подаваемого на пропорциональный ИМ, необходимо дополнительно выполнить операцию интегрирования:
. (9)
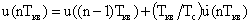
Исследования показали, что САР с таким регулятором имеет существенно лучшие показатели эффективности, чем с ПИД-регулятором. Особенно это проявляется для существенно нестационарных объектов управления.
При необходимости рассмотренный алгоритм регулирования может быть расширен, например, за счет реализации второго порядка астатизма.
The regulator of variable structure with forecasting the free movement, oriented on application in systems of automatic control by objects of technological type is considered. The regulator provides essential increase of efficiency SAR, in particular for appreciably non-stationary objects. The questions of its digital realization and quasioptimal adjustments are worked. The regulator is positioned as alternative to typical PID-regulators.
1. Наладка средств автоматизации и автоматических систем регулирования: Справочное пособие / А.С. Клюев, А.Т. Лебедев, С.А. Клюев, А.Г. Товарнов; Под ред. А.С. Клюева. – 2-е изд., перераб. и доп. – М.: Энергоатомиздат, 1989. – 368 с.: ил.
3. Хобін В.А., Парамонов О.І. Регулятор змінної структури для побутових ефективних робастних автоматичних систем // В кн.: Наук. пр. / Одес. держ. акад. харч. техн. – Одеса, 1997. – Вип. 17. – С. 241 – 248.
4. Справочник по теории автоматического управления / Под ред. А.А. Красовского. – М.: Наука, 1987. – 712 с.
5. Системы с переменной структурой и их применение в задачах автоматизации полета / Под ред. Б.Н. Петрова и С.В. Емельянова. – М.: Наука, 1968. – 324 с.
6. Системное проектирование средств автоматизации / С.В. Емельянов, Н.Е. Костылева, Б.П. Матич, Н.Н. Миловидов. – М.: Машиностроение, 1978. – 190 с.
7. Хобин В.А. Системы гарантирующего управления: структуры с расчетом уставок контурам регулирования // Пр. Міжнар. конф. з автомат. управління (Львів. – 11 – 15 вересня 2000). – Т. 1 – Математичні проблеми управління, оптимізації та теорії ігор. – Львів, ДНДІ інформаційної інфраструктури, 2000. – С. 269 – 273.