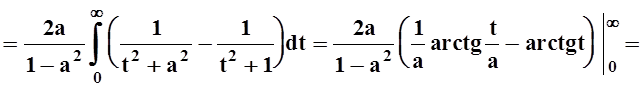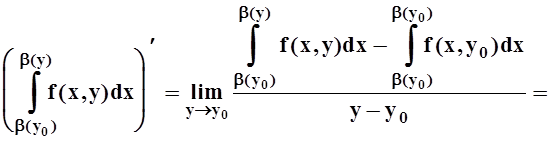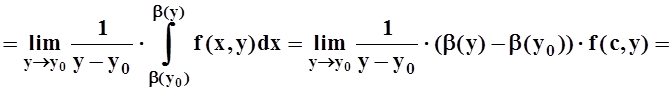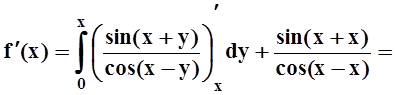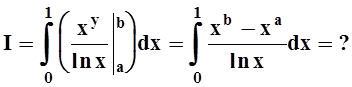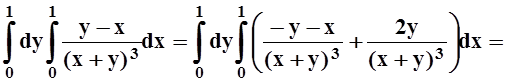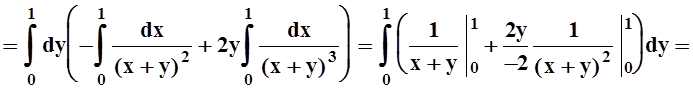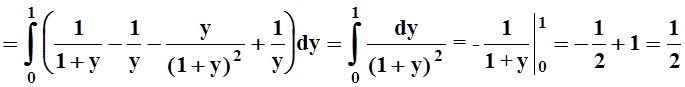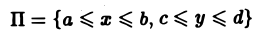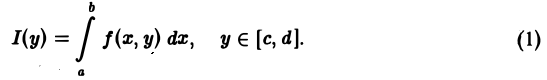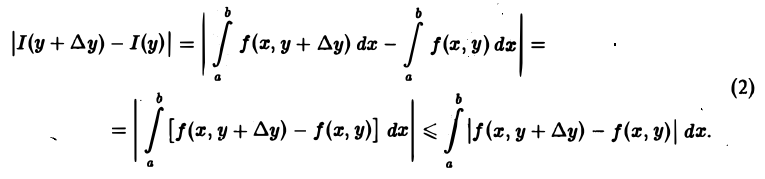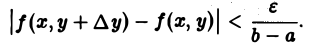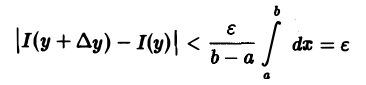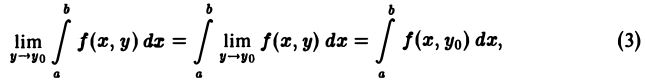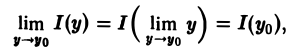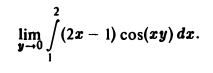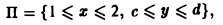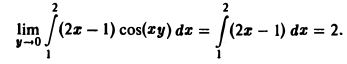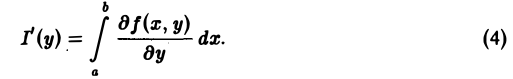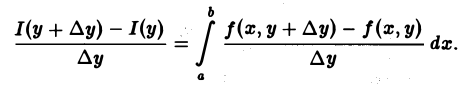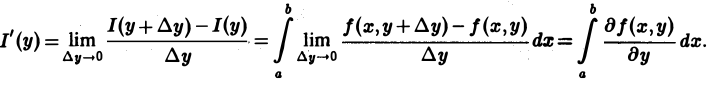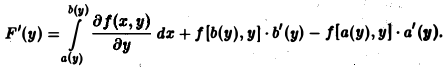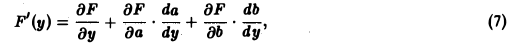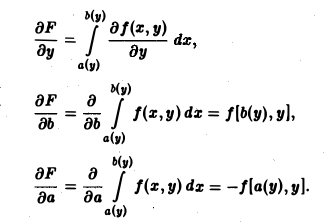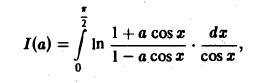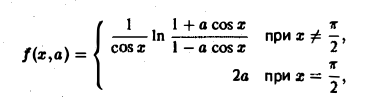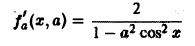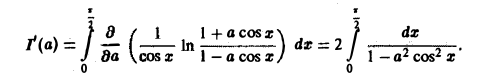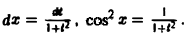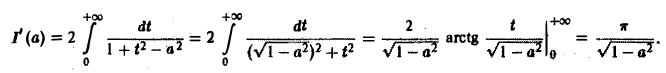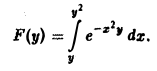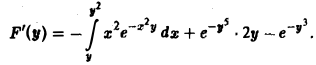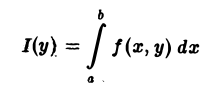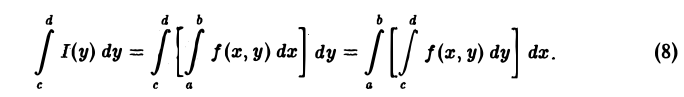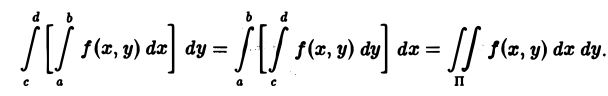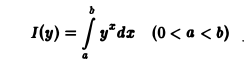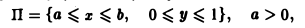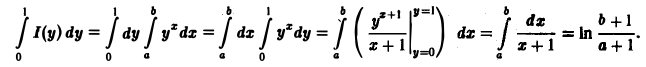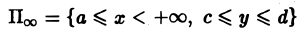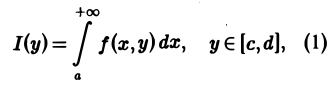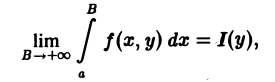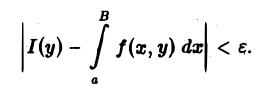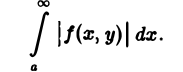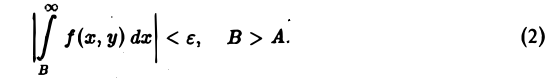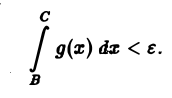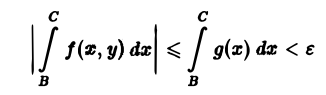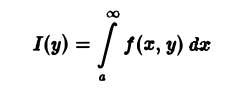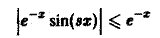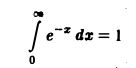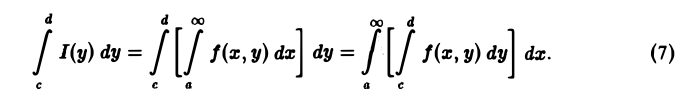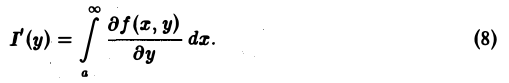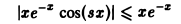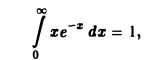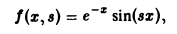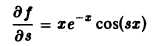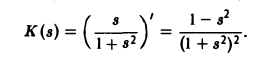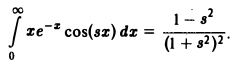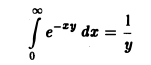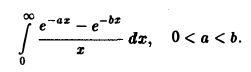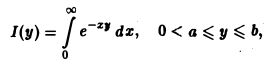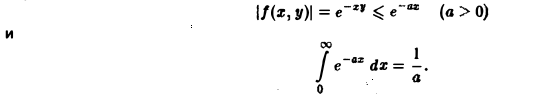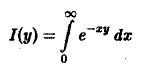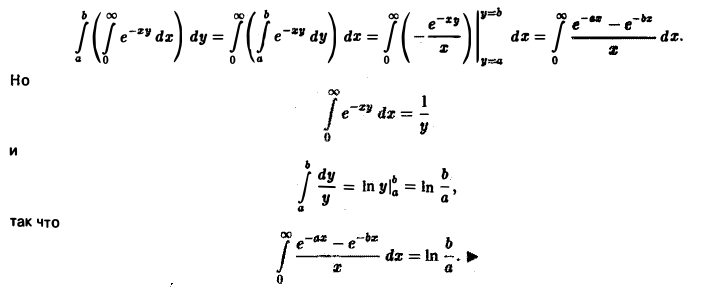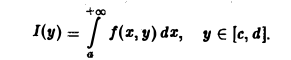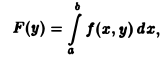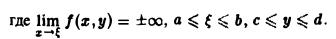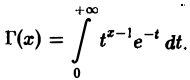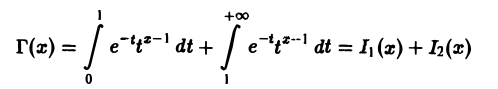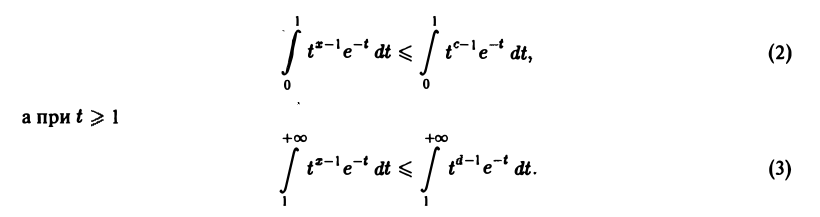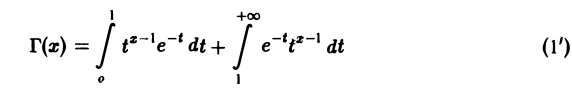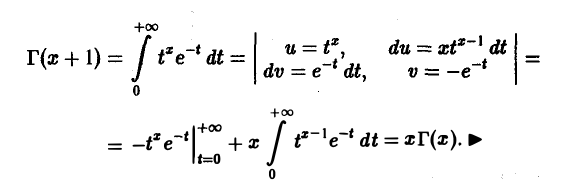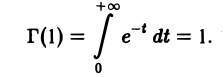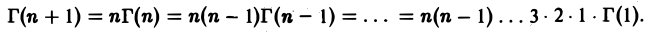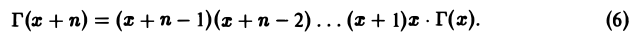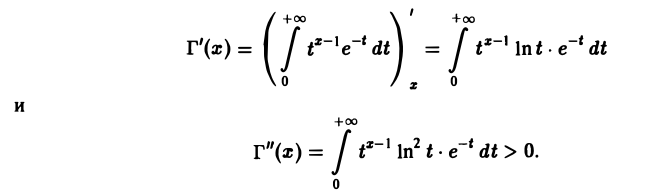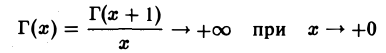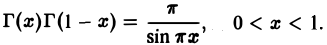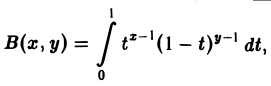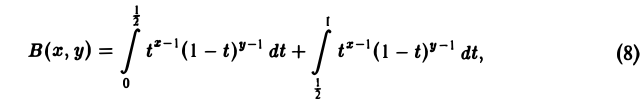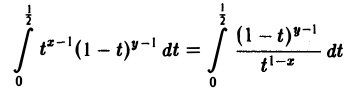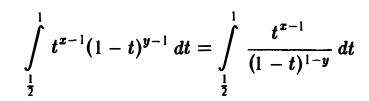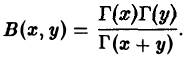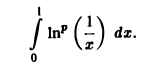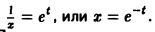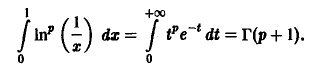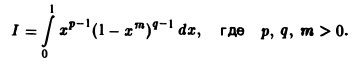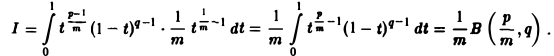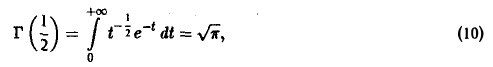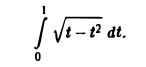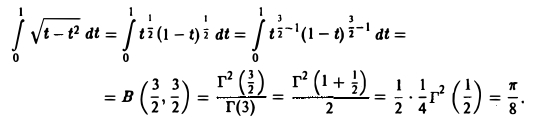с помощью дифференцирования по параметру вычислить интеграл
Интегралы, зависящие от параметра
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
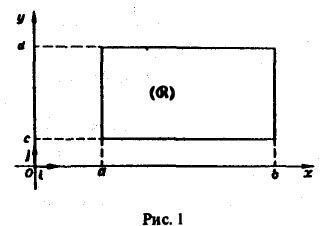
Собственные интегралы, зависящие от параметра 1.1. Понятие интеграла, зависящего от параметра, и его непрерывность Пусть в прямоугольнике определена функция двух переменных f(x, у) (рис. 1). Предположим, что при любом фиксированном значении у е [с, d] существует интеграл ь Ясно, что этот интеграл является функцией переменного у, Интеграл (1) называется интегралом, зависящим от параметра у. Имеет место следующая теорема о непрерывности интеграла, зависящего от параметра.
Теорема 1:
Если функция /(х, у) непрерывна в прямоугольнике П, то функция /(у), определенная соотношением (1), непрерывна на отрезке [с, d\. Из формулы (1) вытекает, что приращение ) функции /(у), соответствующее приращению аргумента Ду, можно оценить так: По условию теоремы функция f
Возможно вам будут полезны данные страницы:
Интеграл (1) называется абсолютно сходящимся на отрезке [с, d\, если сходится интеграл Собственные интегралы зависящие от параметра Дифференцирование интеграла no параметру Интегрирование интеграла по параметру Понятие несобственного интеграла первого рода, зависящего от параметра Равномерная сходимость несобственного интеграла Критерий Коши Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра 2.2. Равномерная сходимость несобственного интеграла. Критерий Коши Определение 2.
Несобственный интеграл
Несобственный интеграл (1) называется равномерно сходящимся по параметру у наотрезке [с, d), если он сходится наэтомотрезкеи для любого е > 0 можно указать такое А ^ а, зависящее только от е, что для всех В > А и для всех у из отрезка [с, d\ выполняется неравенство Имеетместоследующий критерий Коши равномерной сходимости несобстве нных интегралов, зависящих от параметра.
Теорема 4. Для того, чтобы несобственный интеграл (1) равномерно сходился по параметру у на отрезке [с, d\, необходимо и достаточно, чтобы для любого е > 0 можно было указать число А ^ а, зависящее только от е и такое, что для любых В и С, больших А, и для всех у из отрезка [с, d] выполнялось неравенство Справедливость этого критерия вытекает непосредственно из определения равномерной сходимости. Сформулируем достаточный признак равномерной сходимости несобственных интегралов, зависящих от параметра. Теорема 5 (признак Вейерштрасса).
Пусть функция /(х, у) определена в пыупыосе Поо и для каждого у € | с, d] интегрируема по х на любом отрезке [а, Л]. Пусть, кроме того, для всех точек полуполосы П^ выполняется неравенство Тогда из сходимости интеграла f g(x) dx вытекает равномерная сходимость по у наот- резке [с, d] несобственного интегрша В силу критерия Коши сходимости интеграла от функции для любого е > О можно указать число А ^ а такое, что при всех С > В ^ А выполняется неравенство Используя неравенство (4), отсюда получим, что для всех у из отрезка Тем самым, критерий Коши равномерной сходимости интеграла выполнен. Цитр 1.
Иссладова тъ на равномерную сходимость несобственный иктграл где я — параметр, Так как при любом произвольные вещественные числа, выполняется неравенство и интеграл сходится, то по признаку Вейерштрасса интеграл (5) равномерно сходится для всех 2.3. Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра Свойство 1. Непрерывность несобственного интеграла по параметру. Если функция непрерывна в области Поо и интеграл сходится равномернопо у наотрезкс (с, dj,то функция 1(у) непрерывна на Свойство 2. Интегрируемость несобственно го интеграла по параметру.
В самом деле, при любом в, и откуда по признаку Вейерштрасса следует равномерная сходимость интеграла (9). Обозначая подынтегральную функцию интеграла (5) через замечаем, что — подынтегральная функция равномерно сходящегося интеграла (9). Используя свойство дифференцируемое™ несобственного интеграла по параметру, получим Так как 1($) = (в этом легко убедиться путем интегрирования по частям), то Отсюда Пример 3.
Покажем сначала, что несобственный интеграл Собственные интегралы зависящие от параметра Дифференцирование интеграла no параметру Интегрирование интеграла по параметру Понятие несобственного интеграла первого рода, зависящего от параметра Равномерная сходимость несобственного интеграла Критерий Коши Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра зависящий от параметра у, сходится равномерно на отрезке (а, 6).
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Дифференцирование по параметру иногда можно применять для вычисления интегралов.
Пример 5. Вычислить 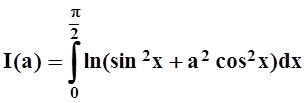
Решение. Найдём производную интеграла по параметру а. Легко проверить, что требования теоремы 4 соблюдены, поэтому
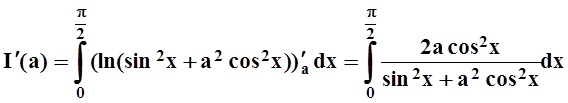
Применим подстановку t= tgx. Тогда 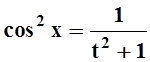
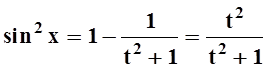
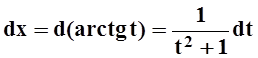
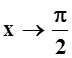
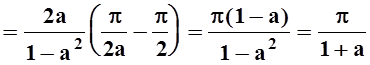
Теперь, вычисляя интеграл, получим:
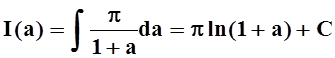
Константу С найти легко, так как


Научимся теперь вычислять производные в случае, если от параметра зависит не только подинтегральная функция, но и пределы интегрирования.
Теорема 5. Пусть f(x,y), 
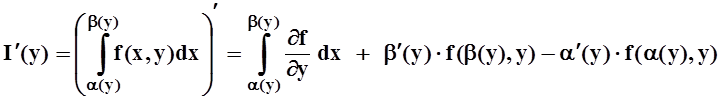
Доказательство. Возьмём произвольную точку y0Î[c, d] и вычислим по определению: 
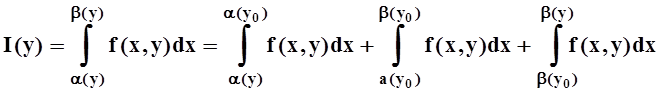
Производная 2–го слагаемого вычисляется по теореме 4:
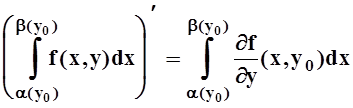
Найдём производную 3–го слагаемого:
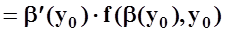
Мы воспользовались теоремой о среднем для определённого интеграла, а затем – непрерывностью f(x,y) и дифференцируемостью b(y). В точности так же вычисляется и производная 1–го слагаемого:
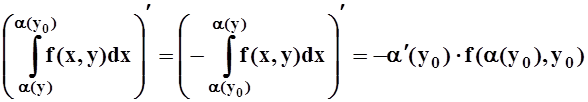
Складывая все 3 слагаемые, получим требуемую формулу (в произвольной точке y0Î[c, d]).
Пример 6. Найти производную функции
Решение. Здесь требуется дифференцировать интеграл по параметру х. Действуем по формуле теоремы 5:
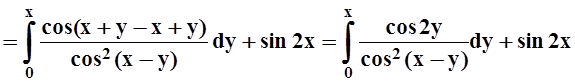
16.1.3 Интегрирование по параметру.
Теорема 6. Пусть f(x,y) непрерывна в прямоугольнике D= [a,b]´ [c,d]. Рассмотрим 
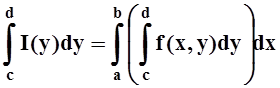
Или, что то же самое,
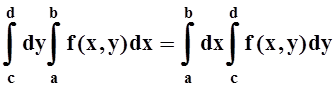
Доказательство. Докажем более общее соотношение. Пусть t –произвольная точка отрезка [c, d]. Докажем, что

Найдём производную по t от каждой части этого равенства. Применяя теорему 5 (или давно известную нам теорему об интеграле с переменным верхним пределом), получим:
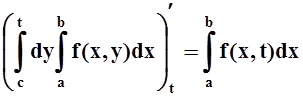
В правой части равенства (*) – интеграл, зависящий от параметра t. Дифференцируем его, применяя теорему 4:
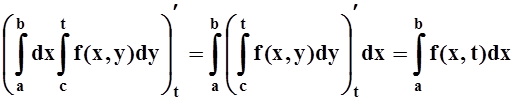
Одинаковые результаты говорят о том, что функции в левой и правой частях равенства (*) отличаются лишь на константу: 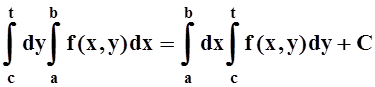
Пример 7. Вычислить интеграл 
Решение. Интегрирование в указанном порядке затруднительно:
Пользуясь теоремой 6, изменим порядок интегрирования.
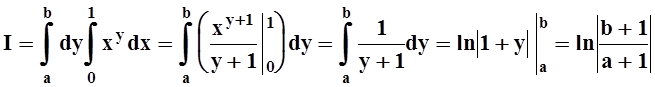
Интеграл вычислен. Попутно получено соотношение:
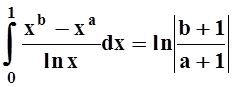
Приведём пример, показывающий, что при нарушении непрерывности подинтегральной функции изменение порядка интегрирования может привести к другому результату.
Пример 8. Вычислим интеграл:
При вычислении в другом порядке можно заметить, что если сменить знак подинтегральной функции, то получится уже рассмотренный интеграл:
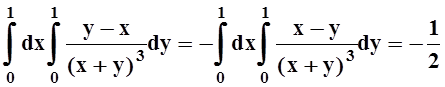
Разные ответы – из–за того, что подинтегральная функция в точке (0, 0) имеет разрыв.
16.2 Несобственные интегралы с параметром
Перейдём к изучению несобственных интегралов, зависящих от параметра. Наиболее простая запись такого интеграла – это по–прежнему

При изучении несобственных интегралов вида 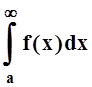
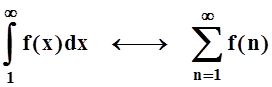
Похожая ситуация имеет место и для несобственных интегралов, зависящих от параметра. Но здесь аналогия устанавливается не с числовыми, а с функциональными рядами:
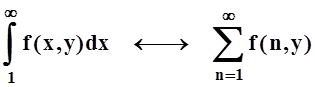
Функциональные ряды мы изучали в 14 модуле, теперь можно сравнить и сопоставить их свойства со свойствами несобственных интегралов с параметром.
Важным в теории функциональных рядов было понятие равномерной сходимости. Оказывается, и здесь оно играет ключевую роль.
Дадим определения. Интеграл 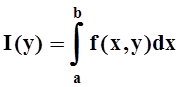
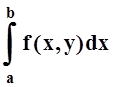
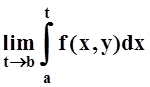
Будем говорить, что 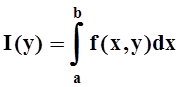
Интегралы, зависящие от параметра с примерами решения и образцами выполнения
Понятие интеграла, зависящего от параметра, и его непрерывность:
Пусть в прямоугольнике
определена функция двух переменных f(x,y) (рис. 1).
Предположим, что при любом фиксированном значении у ∈ [с, d] существует интеграл
Ясно, что этот интеграл является функцией переменного у,
Интеграл (1) называется интегралом, зависящим от параметра у.
Имеет место следующая теорема о непрерывности интеграла, зависящего от параметра.
Теорема:
Если функция f(x, у) непрерывна в прямоугольнике П, то функция I(у), определенная соотношением (1), непрерывна на отрезке [с, d].
Из формулы (1) вытекает, что приращение ∆I = I(у + ∆у) — I(у) функции I(у), соответствующее приращению аргумента ∆у, можно оценить так:
По условию теоремы функция f(x, у) непрерывна в замкнутом прямоугольнике П, а значит, f(x,y) равномерно непрерывна в этом прямоугольнике. Следовательно, для любого ε > 0 можно указать такое δ > 0, что при всех х из [а, b] и всех у и у + ∆у из [с, d] таких, что | ∆у|
Отсюда и из оценки (2) получаем, что
при |∆у|
где уо — любое фиксированное число, принадлежащее отрезку [с, d],
Так как функция I(у) непрерывна на [с, d], то имеют место равенства
равносильные равенствам (3).
Пример:
f(x, у) = (2x — 1) cos(xy)
непрерывна в любом прямоугольнике
где с
Дифференцирование интеграла no параметру
Теорема:
Если функция f(x, у) и ее частная производная 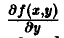
Предполагая, что у + ∆у ∈ [с, d], составим разностное отношение
Переходя в этом равенстве к пределу при ∆у —> 0 и пользуясь непрерывностью частной производной 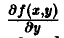
Замечание:
Пусть пределы интегрирования зависят от параметра у. Тогда
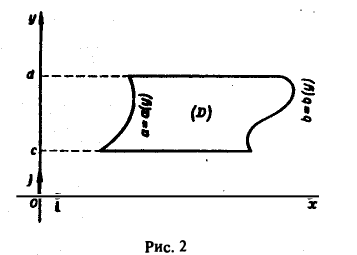
где а(у) ≤ х ≤ b(у) и функции а(у) и b(у) дифференцируемы на отрезке с ≤ у ≤ d. При условии, что функции f(x, у) и f`y(x, у) непрерывны в области D = (рис. 2), получаем, что функция F(y) дифференцируема на [с, d], причем
(6)
Формула (6) доказывается с помощью дифференцирования сложной функции.
Так как F(у) = F(у, а(у), b(у)), то полная производная
Подставляя выражения для производных 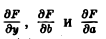
Пример:
Применяя дифференцирование по параметру, вычислить интеграл
где |a|
а также ее производная по параметру
непрерывны в прямоугольнике
Поэтому применима теорема 2 о дифференцировании интеграла по параметру при |а| ≤ 1 — ε
Положим tg x = t, тогда
Интегрируя no t от 0 до + ∞, получим
Отсюда I(a) = π arcsin a + С. Устремляя a к нулю и замечая, что I(0) = 0, имеем С = 0. Следовательно, I(a) = π arcsin а.
Пример:
Найти производную F'(y) для функции
Интегрирование интеграла по параметру
Теорема:
Если функция f(x, у) непрерывна в прямоугольнике П = <а≤ x ≤ b, с ≤ у ≤ d>, то функция
интегрируема на отрезке [с, d], причем справедливы равенства
Другими словами, если f(x, у) непрерывна в П, то интеграл, зависящий от параметра, можно интегрировать по параметру под знаком интеграла.
Согласно теореме 1, функция I(у) непрерывна на отрезке [с, d] и поэтому интегрируема на нем. Справедливость формулы (8) следует из равенства повторных интегралов,
Пример:
Проинтегрировать по параметру у интеграл
в пределах от 0 до 1.
Так как функция f(х, у) = у x непрерывна в прямоугольнике
то применима теорема 3 об интегрировании интеграла по параметру. Имеем
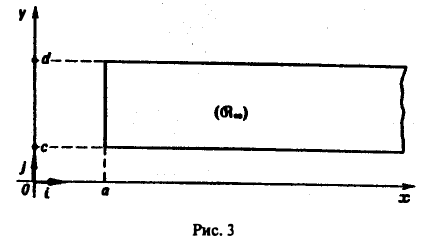
Несобственные интегралы, зависящие от параметра
Понятие несобственного интеграла первого рода, зависящего от параметра:
Пусть функция двух переменных f(х, у) определена в полуполосе
(рис.3) и при каждом фиксированном у ∈ [с, d] существует несобственный интеграл 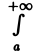
называется несобственным интегралом первого рода, зависящим от параметра у. Интервал (с, d) может быть и бесконечным.
Определение:
Несобственный интеграл (1) называется сходящимся в точке у ∈ [с, d], если существует конечный предел
т.е. если для любого ε > 0 существует число Во такое, что для всех В ≥ Вo выполняется неравенство
Если несобственный интеграл (1) сходится в каждой точке у отрезка [с, d], то он называется сходящимся на этом отрезке. Интеграл (1) называется абсолютно сходящимся на отрезке [с, d], если сходится интеграл
Равномерная сходимость несобственного интеграла. Критерий Коши
Определение:
Несобственный интеграл (1) называется равномерно сходящимся по параметру у на отрезке (с, d), если он сходится на этом отрезке и для любого ε > 0 можно указать такое А ≥ а, зависящее только от ε, что для всех В > А и для всех у из отрезка [с, d] выполняется неравенство
Имеет место следующий критерий Коши равномерной сходимости несобственных интегралов, зависящих от параметра.
Теорема:
Для того, чтобы несобственный интеграл (1) равномерно сходился по параметру у на отрезке [с, d], необходимо и достаточно, чтобы для любого ε > 0 можно было указать число А ≥ а, зависящее только от ε и такое, что для любых В и С, больших А, и для всех у из отрезка [с, d] выполнялось неравенство
Справедливость этого критерия вытекает непосредственно из определения равномерной сходимости.
Сформулируем достаточный признак равномерной сходимости несобственных интегралов, зависящих от параметра.
Теорема:
Признак Вейерштрасса. Пусть функция f(x,y) определена в полуполосе 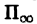
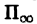
Тогда из сходимости интеграла 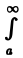
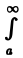
В силу критерия Коши сходимости интеграла от функции g(х), для любого ε > О можно указать число А ≥ а такое, что при всех С > В ≥ А выполняется неравенство
Используя неравенство (4), отсюда получим, что
для всех у из отрезка [с, d). Тем самым, критерий Коши равномерной сходимости интеграла
Пример:
Исследовать на равномерную сходимость несобственный интеграл
Так как при любом s ∈ [а, β], где а и β — произвольные вещественные числа, выполняется неравенство
сходится, то по признаку Вейерштрасса интеграл (5) равномерно сходится для всех s ∈ [а, β].
Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра
Свойство:
Непрерывность несобственного интеграла по параметру. Если функция f(х, у) непрерывна в области 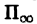
сходится равномерно по у на отрезке [с,d], то функция I(у) непрерывна на [с, d].
Свойство:
Интегрируемость несобственного интеграла по параметру. Если функция f(x, у) непрерывна в области 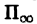
Свойство:
Дифференцируемого несобственного интеграла по параметру. Пусть функция f(x,y) и ее частная производная 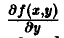
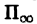
сходится равномерно по у на [с, d]. Тогда
Пример:
Вычислить интеграл, зависящий от параметра s,
В примере 1 мы доказали равномерную сходимость интеграла
по параметру s на любом отрезке [a, β]. Покажем, что интеграл (9) также равномерно сходится по параметру s на любом отрезке [а, β]. В самом деле,
откуда по признаку Вейерштрасса следует равномерная сходимость интеграла (9). Обозначая подынтегральную функцию интеграла (5) через f(x, s),
— подынтегральная функция равномерно сходящегося интеграла (9). Используя свойство дифференцируемости несобственного интеграла по параметру, получим
K(s)=I'(s).
Так как I(s) = 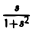
Пример:
по у, у > 0, найти интеграл
Покажем сначала, что несобственный интеграл
зависящий от параметра у, сходится равномерно на отрезке [a, b]. Это вытекает из признака Вейер-штрасса, так как
по параметру у в пределах от а до b. Имеем
Замечание:
До сих пор мы рассматривали несобственные интегралы вида
Эго несобственные интегралы первого рода, зависящие от параметра у. Несобственным интегралам второго рода, зависящим от параметра у, называется интеграл вида
Теория несобственных интегралов второго рода, зависящих от параметра, аналогична рассмотренной нами теории для несобственных интегралов первого рода, зависящих от параметра.
Интегралы Эйлера. Гамма-функция и ее свойства
Гамма-функцией называется интеграл
(1)
Область определения гамма-функции Г(х)
В интеграле (1) имеются особенности двух типов: ^интегрированиепо полупрямой 0 ≤ t
и рассмотрим каждый из них отдельно.
Так как 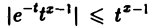
Интеграл I2(x) сходится при любом х. В самом деле, взяв произвольное λ > 1, получим, что при любом х
При λ > 1 интеграл 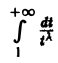
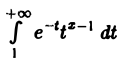
Тем самым, 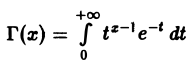
Покажем, что интеграл (1) сходится равномерно по х на любом отрезке [с, d], где 0
Интегралы в правых частях формул (2) и (3) сходятся, а по признаку Вейерштрасса равномерно сходятся интегралы, стоящие в левых частях неравенств (2) и (3). Следовательно, в силу равенства
получаем равномерную сходимость Г(x) на любом отрезке [с, d], где 0 0.
Некоторые свойства гамма-функции
1, Г(х) > 0 при х > О (гамма-функция при х > 0 не имеет нулей).
2. При любом х > 0 имеет место формула приведения для гамма-функции
Г(х + 1) = хГ(x). (4)
3. При x = n имеет место формула
Г(n + 1) = n! (5)
Пользуясь формулой (4), получим
Применяя формулу (4) п раз, при х > 0 получаем
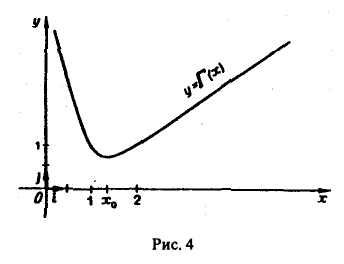
4. Кривая у = Г(х) выпукла вниз. В самом деле,
Отсюда следует, что производная Г'(х) на полупрямой (0, + ∞) может иметь только один нуль. А так как Г(1) = Г(2) = 1, то по теореме Ролля этот нуль х0 производной Г'(х) существует и лежит в интервале (1,2). Поскольку Г»(х) > 0, то в точке х0 функция Г(х) имеет минимум.
Можно показать, что на (0, + ∞) функция Г(х) дифференцируема любое число раз.
5. Из формулы Г(х + 1) = хГ(х) следует, что
(ибо Г(х) непрерывна и Г(х+1) → Г(1) = 1 при х → +0).
6. Формула дополнения.
График гамма-функции имеет вид, изображенный на рис. 4.
Бета-функция и ее свойства
Бета-функцией называется интеграл
(7)
зависящий от параметров х и у.
Область определения бета-функции В (x)
Подынтегральная функция при х
первый из которых (при х
— несобственный интеграл 2-го рода. Он сходится при условии, что 1-х 0, а интеграл
сходится при у > 0. Тем самым, бета-функция В(х, у) определена для всех положительных значений х и у.
Можно доказать, что интеграл (7) равномерно сходится в каждой области x≥ а > 0, у ≥ b > 0, так что бета-функция непрерывна при х > 0, у > 0.
Некоторые свойства бета-функции
1, При х > 0 и у > 0 справедлива формула
(9)
2. Бета-функция является симметричной относительно х и у, т. е.
В(х, у) = В(у, х).
Это следует из формулы (9).
Применение интегралов Эйлера в вычислении определенных интегралов
Рассмотрим несколько примеров.
Пример:
Введем замену
Тогда 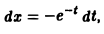
Пример 2. Вычислить интеграл
Положим х m = t, тогда 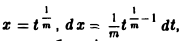
Пример:
Исходя из равенства
Здесь мы воспользовались определением бета-функции и формулами (9), (4), (5) и (10).
Определение интегралов, зависящих от параметра; их непрерывность и интегрируемость по параметру


Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института