scilab что это за программа
Scilab
Scilab (читается Сайлэб) — пакет прикладных математических программ, предоставляющий мощное открытое окружение для инженерных (технических) и научных расчётов.
Содержание
История
С 1994 года распространяется вместе с исходным кодом через Интернет. В 2003 году для поддержки Scilab был создан консорциум Scilab Consortium. Сейчас в него входят 25 участников, в том числе Mandriva, INRIA и ENPC (Франция).
Возможности
Scilab содержит сотни математических функций, и есть возможность добавления новых, написанных на различных языках (C, C++, Fortran и т. д.). Также имеются разнообразные структуры данных (списки, полиномы, рациональные функции, линейные системы), интерпретатор и язык высокого уровня.
Scilab был спроектирован как открытая система, и пользователи могут добавлять в него свои типы данных и операции путём перегрузки.
В системе доступно множество инструментов:
Scilab имеет схожий с MATLAB язык программирования. В состав пакета входит утилита, позволяющая конвертировать документы Matlab в Scilab.
Scilab позволяет работать с элементарными и большим числом специальных функций (Бесселя, Неймана, интегральные функции), имеет мощные средства работы с матрицами, полиномами (в том числе и символьно), производить численные вычисления (например, численное интегрирование) и решение задач линейной алгебры, оптимизации и симуляции, мощные статистические функции, а также средство для построения и работы с графиками.
В состав пакета также входит Scicos — инструмент для редактирования блочных диаграмм и симуляции (аналог simulink в пакете MATLAB). Имеется возможность совместной работы Scilab с программой LabVIEW.
Распространение
Программа доступна для различных операционных систем, включая Linux и Microsoft Windows. Возможности Scilab могут быть расширены внешними программами и модулями, написанными на разных языках программирования. Программа имеет открытый исходный код, что позволяет как свободное коммерческое использование и распространение неизменённых версий, так и некоммерческое распространение измененных версий, которые должны включать в себя исходный код. Для коммерческого распространения измёненных версий необходимо согласование с INRIA.
Начиная с версии 5.0 программа распространяется под совместимой с GNU GPL 2 лицензией CeCILL.
Отличительные особенности
Отличия от некоторых коммерческих программ:
Примеры
Простые вычисления
Код, задающий матрицу и считающий определитель:
Scilab — от поиска факториала до крестиков-ноликов
За картинку спасибо DrZugrik
Итак для начала краткая справка. Что же такое Scilab?
Подробный ответ на этот вопрос можно узнать на Википедии или на официальном сайте сообщества
Если рассказать своими словами – то Scilab, это открытий аналог Matlab. С очень похожим синтаксисом, с похожими процедурами (многие процедуры Matlab имеют свой аналог в Scilab), Интерфейс самой свежей Scilab 5.4.1, чем-то отдаленно напоминает Matlab пятилетней давности, теперь в нем вполне комфортно работать. Ну и самое главное Scilab имеет схожие возможности, безусловно меньшие чем у коммерческого гиганта, но все же для студента, начинающего ученого или просто любопытного инженера вполне достаточные. У Scilab есть свой аналог Simulink (правда явно уступающий), также можно подключать различные модули, например Maxima для символьных вычислений (у меня работало не очень надежно, но работало).Scilab есть под Windows и Linux, есть исходники, выпускается под открытой лицензией. Чем не замена пиратским копиям Matlab, установленным в колледжах и университетах?
Пример работы пакета прикладных математических программ можно увидеть на скриншотах под спойлером.
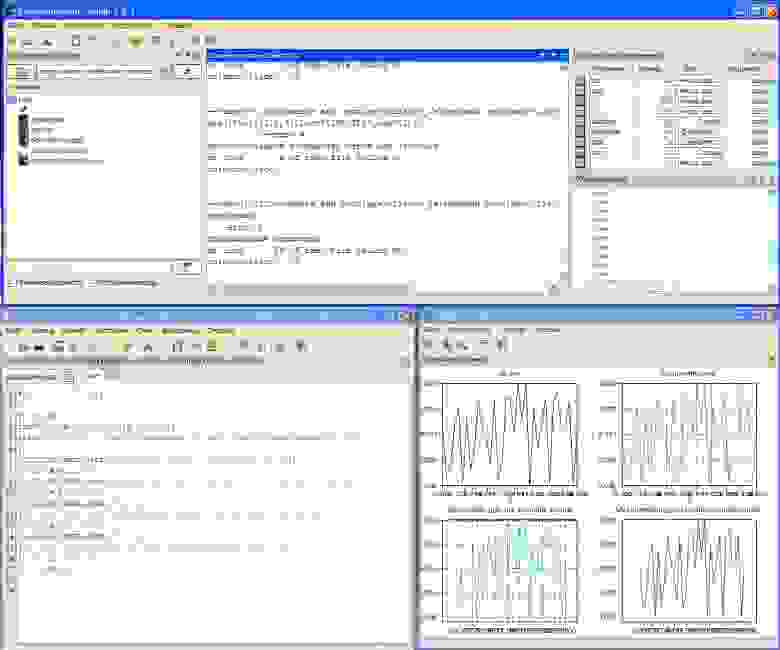
графики в Scilab
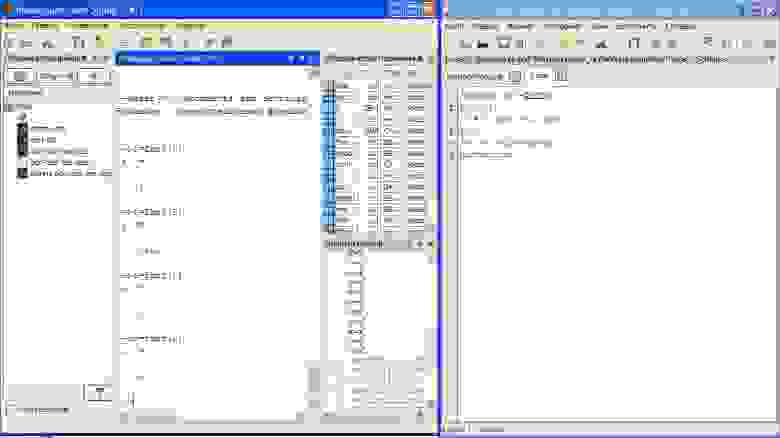
пример функции — нахождение факториала
Какая стояла задача.
С помощью возможностей по созданию графических интерфейсов в Scilab, написать простенькие крестики нолики для игры с компьютером.
Исходный код (выложены на GitHub ) представлен под спойлером
Если вкратце его описать, то вначале создается графическое окно, на нем размещается 9 кнопок игрового поля, текстовая метка и кнопка перезапуска. При нажатии на кнопку на игровом поле начинается игра. Искусственный интеллект, чисто с потолка берет значение от 1 до 9 и если оно свободно «ходит» туда, если нет копает дальше. В конце каждого обработчика нажатия, вызывается проверка выполнения условия победы (ячейки поля представляем как матрицу и всячески над ней издеваемся) В итоге получились простенькие крестики нолики для игры с AI, который в ходе тестов иногда меня неожиданно обыгрывал.
Выглядит это как-то так:
Безусловно код плохой, но надеюсь, что я смогу кого-нибудь мотивировать на изучение этого безусловно полезного математического инструмента.
Всем хорошей пятницы и прекрасных выходных 🙂
Основы работы в SciLab. На примере экзаменационных вопросов по КСВЭ
Завтра мне сдавать экзамен по такому предмету как КСВЭ(Компьютерный сервис вычислительного эксперимента). А лучший способ подготовки — это написание статьи. Я рассмотрю часть вопросов к экзамену, которые связаны с SciLab.
Статья больше подходит для студентов, использующих scilab для проверки решения, для или для сдачи экзамена по дисциплине КСВЭ. Для более подробного изучения надо читать литературу, указанную в конце статьи
Основные термины
Scilab (читается Сайлэб) — пакет прикладных математических программ, предоставляющий мощное открытое окружение для инженерных (технических) и научных расчётов.
CeCILL (от «CEA CNRS INRIA Logiciel Libre») — это лицензия на свободное программное обеспечение, адаптированная к интернациональному законодательству и законодательству Франции, подобная GNU General Public License и сохраняющая совместимость с ним.
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида 
Обыкнове́нные дифференциа́льные уравне́ния (ОДУ) — это дифференциальное уравнение вида 
где — неизвестная функция (возможно, вектор-функция, тогда, как правило, тоже вектор-функция со значениями в пространстве той же размерности; в этом случае говорят о системе дифференциальных уравнений), зависящая от независимой переменной, штрих означает дифференцирование по. Число (порядок старшей производной, входящей в данное уравнение) называется порядком дифференциального уравнения (1)
1. Система компьютерной математики SciLab: История разработки. Возможности и ключевые особенности. Достоинства и недостатки.
История
С 1994 года распространяется вместе с исходным кодом через Интернет. В 2003 году для поддержки Scilab был создан консорциум Scilab Consortium. Сейчас в него входят 25 участников, в том числе Mandriva, INRIA и ENPC (Франция).
Scilab содержит сотни математических функций, и есть возможность добавления новых, написанных на различных языках (C, C++, Fortran и т. д.). Также имеются разнообразные структуры данных (списки, полиномы, рациональные функции, линейные системы), интерпретатор и язык высокого уровня.
Scilab был спроектирован как открытая система, и пользователи могут добавлять в него свои типы данных и операции путём перегрузки.
В системе доступно множество инструментов:
2D и 3D графики, анимация
Линейная алгебра, разреженные матрицы (sparse matrices)
Полиномиальные и рациональные функции
Интерполяция, аппроксимация
Симуляция: решение ОДУ и ДУ
Scicos: гибрид системы моделирования динамических систем и симуляции
Дифференциальные и не дифференциальные оптимизации
Обработка сигналов
Параллельная работа
Статистика
Работа с компьютерной алгеброй
Интерфейс к Fortran, Tcl/Tk, C, C++, Java, LabVIEW
Scilab имеет схожий с MATLAB язык программирования. В состав пакета входит утилита, позволяющая конвертировать документы Matlab в Scilab.
Scilab позволяет работать с элементарными и большим числом специальных функций (Бесселя, Неймана, интегральные функции), имеет мощные средства работы с матрицами, полиномами (в том числе и символьно), производить численные вычисления (например, численное интегрирование) и решение задач линейной алгебры, оптимизации и симуляции, мощные статистические функции, а также средство для построения и работы с графиками.
Для численных расчётов используются библиотеки Lapack, LINPACK, ODEPACK, Atlas и другие.
В состав пакета также входит Scicos — инструмент для редактирования блочных диаграмм и симуляции (аналог simulink в пакете MATLAB). Имеется возможность совместной работы Scilab с программой LabVIEW.
Ключевые особенности
Отличия от некоторых коммерческих программ:
Бесплатность.
Свободность (с версии 5.0).
Маленький размер — дистрибутив 4 версии занимал менее 20 МБ против более чем двухгигабайтного пакета MATLAB. Инсталлятор 5 версии (5.4.0) увеличился в объёме до 108 МБ.
Возможность запуска в консоли без использования графического интерфейса, в том числе в версии под Windows (в UNIX и Windows версиях MatLab-а эта возможность присутствует тоже). Это позволяет производить автоматизированные вычисления, есть пакетный режим.
Достоинства и недостатки
Поиски достоинства и недостатков на просторе интернета ни чего не дали. Так что расскажу о том, что я заметил сам.
Если говорить о достоинствах, тут самым основным для меня является бесплатность данного пакета, по сравнению с той же Mathematic, когда для выполнения лабораторных работы приходилось искать серийник или crack. Далее — это кросплатформеность, т.к. я больше предпочитаю использовать Gentoo, чем Windows. В принципе большенство достоинств описано в пункте Ключевые особенности.
Из недостатков я вижу только 2: Это нет такой визуализации программирования как в Mathematic, а так же система использует прежде всего численные подходы, для вычисления, что может сказаться на точности.
2. Основы работы в SciLab. Пользовательские и системные переменные. Математические выражения. Коментарии
При написании данной статьи я использую версию scilab-5.3.3 под windows.
SciLab 5.3.3
Операционные системы: Windows, Linux, MacOS
Пользовательские и системные переменные
Год/Дата Выпуска: 2011
Версия: 5.3.3
Разработчик: Free Open Source Software for Numerical Computation
Сайт разработчика: www.scilab.org
Разрядность: 32bit+64bit
Лицензия: CeCILL
По характеристикам данных не нашёл, но могу сказать, что данный пакет грузится без глюков на моём ноутбуке
Процессор: Intel Celeron Dual-Core T3300 2.0 ГГц
Оперативная память 2Гб DDR3
Видеоадаптер Intel GMA4500M
Прежде чем перейти дальше, рассмотрим сам интерфейс. При запуске открывается командное окно. 
Есть 2 варианта работы: 1 — это работа в том же командном окне, 2 — открыть SciNotes(что-то вроде блокнота с подсветкой) где можно написать код, который позднее запустить, результат выполнения появится в командном окне.
Для примера я рассмотрю вывод Hellow world.
Командная строка. Используем функцию вывода на дисплей disp()
При работе в SciNotes вы получите что то похожее 
для выполнения кода, надо или нажать на стрелочку в право 🙂 (как во многих средах разработки)
или Выполнение->… без отображение команд
в принципе можно использовать и другие методы выполнения, и не использовать вывод на экран
Результатом выполнения будет: 
т.к. можно сказать что интерфейс изучен, далее я буду приводить просто код и результат выполнения
SciLab чувствителен к реестру, т.е. А и а — разные переменные переменные.
a=1,A=3
//Каждая операция начинается с новой строки или через запятую
//коментарии можно оставлять после двух символоф слэш
b=3
c=a+b
disp©
Основные операции:
+ сложение
— вычитание
* умножение
/ деление справа, т.е. x/y = xy^(-1)
\ деление слева, т.е. x\y = x^(-1)y
^ возведение в степень, т.е. x^y
** возведение в степень (эквивалентно ^)
’ эрмитово сопряжение (комплексное сопряжение и транспонирование)
3. Основы работы в SciLab. Функции и их типы. Способы объявления пользовательских функций. Использование функций. Файлы-сценарии и их применение для хранения функций.
Элементарные математические функции.
acos acosd acosh acoshm acosm acot acotd acoth
acsc acscd acsch asec asecd asech asin asind
asinh asinhm asinm atan atand atanh atanhm atanm
cos cosd cosh coshm cosm cotd cotg coth
cothm csc cscd csch sec secd sech sin
sinc sind sinh sinhm sinm tan tand tanh
tanhm tanm
exp expm log log10 log1p log2 logm max
maxi min mini modulo pmodulo sign signm sqrt
sqrtm
y = int8(x) 8-битовое число со знаком [-2^7; (2^7)-1] = [-128; 127]
y = uint8(x) 8-битовое число без знака [0; (2^8)-1] = [0; 255]
y = int16(x) 16-битовое число со знаком [-2^15; (2^15)-1] = [-32768; 32767]
y = uint16(x) 16-битовое число без знака [0; (2^16)-1] = [0; 65535]
y = int32(x) 32-битовое число со знаком [-2^31; (2^31)-1] = [-2147483648; 2147483647]
y = uint32(x) 32-битовое число без знака [0; (2^32)-1] = [0; 4294967295]
iconvert преобразование к целочисленному представлению
inttype определение типа целого числа
простейший способ вызова пользовательской функции:
пример пользовательской фунции:
function y = myfunction ( x )
y = 2 * x
endfunction
Сохраняем её. Далее приведён пример вызова данной функции
4. Определение одномерный и многомерных массивов. Основные действия над массивами.
Пример, как задаётся одномерный массив:
квадратные скобки ”[” и ”]” обозначают начало и конец перечисления
элементов матрицы,
запятой ”,” отделяются элементы матрицы, находящиеся в одной строке,
точка с запятой ”;” разделяет строки матрицы.
size определить размер матрицы
matrix изменить размер матрицы
resize_matrix создать новую матрицу заданного размера и скопировать
в нее элементы из исходной матрицы
Операции над матрицами:
Обращение к элементам матрицы
i = 1; 2, а j = 3; 4
для этого возьмём уже готовую матрицу
—>A = testmatrix (» hilb «, 5)
A =
25. — 300. 1050. — 1400. 630.
— 300. 4800. — 18900. 26880. — 12600.
1050. — 18900. 79380. — 117600. 56700.
— 1400. 26880. — 117600. 179200. — 88200.
630. — 12600. 56700. — 88200. 44100.
—>A(1: 2, 3: 4)
ans =
1050. — 1400.
— 18900. 26880
A матрица целиком
A(. ) матрица целиком
A(i:j,k) элементы матрицы в k-ом столбце с i-ой по j-ую строку
A(i,j:k) элементы матрицы в i-ой строке с j-ого по k-ый столбец
A(i,:) i-ая строка матрицы
A(:,j) j-ый столбец матрицы
Генерация единичной матрицы
пример умножения числа на еденичную матрицу 2 на 2
5. Определение одномерный и многомерных массивов. Специальные матричные функции
функции работы с матрицами
chol разложение Холесского
companion сопровождающая матрица
cond число обусловленности
det определитель матрицы
inv обратная матрица
linsolve решение систем линейных уравнений
lsq метод наименьших квадратов
lu LU-разложение с выбором опорного элемента
qr QR-разложение
rcond обратное число обусловленности
spec собственные значения и векторы
svd разложение по сингулярным числам матрицы
testmatrix генерация специальных матриц (Гильберта, Франка и др.)
trace след матрицы
6. Определение одномерный и многомерных массивов. Решение СЛАУ. Символьные массивы и операции над ними
Текст файла–сценария с решением задачи по формулам Крамера
7. Численное интегрирование. Подходы к интегрированию. Интегрирование функций заданных пользователем
Численное интегрирование (историческое название: (численная) квадратура) — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла.
Интегрирование по методу трапеций
проинтегрируем функцию, корень из 2*x-1 на отрезке от 1 до 10 с разбиением в 1 шаг
—>x=1:10
x =
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
—>y=sqrt(2*x-1)
y =
column 1 to 6
1. 1.7320508 2.236068 2.6457513 3. 3.3166248
column 7 to 10
3.6055513 3.8729833 4.1231056 4.3588989
—>inttrap(x,y)
ans =
27.211585
Квадратурные формулы Ньютона Котеса
8.Численное дифференцирование. Подходы к дифференцированию.
Численное дифференцирование — совокупность методов вычисления значения производной дискретно заданной функции.
В основе численного дифференцирования лежит аппроксимация функции, от которой берется производная, интерполяционным многочленом. Все основные формулы численного дифференцирования могут быть получены при помощи первого интерполяционного многочлена Ньютона (формулы Ньютона для начала таблицы).
в точке
9. Решение ОДУ средствами SciLab. Функции применяемые для решение ОДУ. Решение краевых задач.
Существует 4 способа для решения ОДУ:
1. С помощью команды ode, которая является солвером для решения обыкновенного
дифференциального уравнения.
2. С помощью команды odedc, которая вычисляет решение смешанной дискретно-
непрерывной системы.
3. Команда dassl, которая дает решение неявно выраженного дифференциального уравнения.
4. С помощью команды impl, которая дает решение неявно выраженного линейного
дифференциального уравнения.
—>y0=1;
—>t0=1;
—>t=1:0.01:1.5;
—>deff(«[ydot]=f(t,y)»,«ydot=y^(1/3)*t»)
—>y=ode(y0,t0,t,f);
—>y_exact=((t^2+2)/3)^(1.5);// это функция точного решения для сравнения
—>my_er=y-y_exact;
—>plot(t,y-y_exact) // это график ошибки вычисления от аргумента t
результатом является такой график 
за одно можно увидеть Графическое окно. Построение графиков будет подробно рассмотрено далее.
10. Построение двухмерных графиков в системе SciLab. Основные функции и типы графиков.
Функция plot
рассмотрим пример:
Функция plot2d
Рассмотрим функцию опять на примере:

как мы можем увидеть, у этой функции намного больше функционала.
фунции передаются сразу массивом, так же можно указать цвет линий и отрезок.
Функция polarplot
Служит для построения графика в полярных координатах
получается ромашка 
параметры похожи как и в случае с plot2d
11. Построение трёхмерных графиков в системе SciLab. Основные функции и типы графиков.
Существует 4 способа построение графика:
Способ 1.
С помощью команды plot3d. Команда создает 3D график по точкам, заданным матрицами
x, y и z.
Способ 2.
С помощью команды plot3d1. Команда создает 3D график по точкам, заданным
матрицами x, y и z с помощью уровней цвета. Вещь в общем избыточная: величина
координаты z дополнительно еще и покрашена, в зависимости от принимаемого значения
z.
Способ 3.
С помощью команды fplot3d. Это аналог команды fplot3d, но изображаемая поверхность
задана с помощью внешней функции.
Способ 4.
С помощью команды fplot3d1. Это аналог команды plot3d1, но изображаемая поверхность
задана с помощью внешней функции.
Синтаксис этих команд смотри с помощью help.

забыл указать, что в графическом окне есть возможность экспорта данных, т.е. сохранить картинку
Результат такой же как в примере 1
результат такой же, как в примере 2
12. Задача полиномов в SciLab. Символьные операции с полиномами. Решение алгебраический уравнений. Сравнение функций fsolve и roots.
Рассмотрим на примере решения уравнения 2x^4-8x^3+8x^2-1=0
Для решения трансцендентных уравнений в применяют функцию Scilab fsolve(x0,f)
задача
Надеюсь данная статья послужит толчком, для дальнейшего изучения SciLab или решения своих задач/лабараторных
Scilab
Scilab — это мощное открытое окружение для инженерных и научных расчётов. К сожалению, при ознакомлении с данной средой автор этого учебника столкнулся с достаточно скудным набором русскоязычной литературы, которая не охватывала всех возможностей этого прекрасного окружения. В этом учебнике автор желает вместить всё, что необходимо знать для полноценной работы в среде.
Как читать учебник [ править ]
Повествование в этом учебнике идёт по нарастанию, от простого к сложному, поэтому настоятельно рекомендуется читать его последовательно. Для понимания материала от пользователя требуются умение работать с операционной системой, в которую установлена среда. Поскольку Scilab это в первую очередь математический пакет, от пользователя требуются знания некоторых математических разделов (арифметика, алгебра, математическая статистика). Также желательно, чтобы пользователь знал, что такое компьютерная программа и структурное программирование.
Автор учебника постарался построить материал в структуру, т.е. первым делом рассматриваются объекты, которые могут быть созданы в данной среде, затем способы манипуляции этими объектами, а затем способы применения этих объектов для решения прикладных задач. Автор попытался отойти от сухого изложения материала, совмещая теорию и практику вместе.
Для эффективного обучения обязательно повторяйте все примеры в этом учебнике и выполняйте задачи для самостоятельного решения.
Основы работы с системой технических расчетов Scilab
Одной из областей использования персональных компьютеров является выполнение математических расчетов. Для этого используются специализированные математические системы, составляющие особый класс прикладного программного обеспечения. Математические системы широко используются как для выполнения инженерных расчетов, так и для проведения научных исследований. Они позволяют выполнять сложные алгебраические преобразования, вычислять пределы, суммы, произведения, производные и интегралы, находить решение дифференциальных уравнений или их систем. При помощи этих систем можно решать задачи аналитической геометрии, теории вероятности и математической статистики, тензорного анализа и линейной алгебры, дискретной математики, теории групп и многих других. Все они имеют замечательные возможности построения двух- и трехмерных графиков, что дает возможность представить в графической форме данные и результаты решения задач. Такие системы постоянно совершенствуются и развиваются на стыке математики и информатики.
Наиболее популярными среди математических систем является Maple, MATLAB, Mathematica и MathCad. Но все эти программы являются коммерческими. В то же время при использовании программного обеспечения все большую остроту приобретает проблема лицензионной чистоты программных продуктов, то есть защита интеллектуальной собственности разработчиков этих продуктов. Одним из путей решения этой проблемы есть использование программ, которые принадлежат к классу freeware, то есть бесплатного программного обеспечения. Очень важным является то, что достаточно часто такое программное обеспечение является еще и «открытым», то есть предоставляет возможность всем желающим не только ознакомиться с исходным программным кодом и уяснить его алгоритм, но и усовершенствовать программный код. Это, в свою очередь, привлекают много желающих для тестирования и усовершенствования такого программного обеспечения, которое зачастую приводит к стремительному развитию программных продуктов. Как раз это и присущее прикладному пакету для выполнения численных расчетов Scilab, о котором в дальнейшем и пойдет речь.
Пакет Scilab позволяет решать ряд задач:
Программа принадлежит к классу freeware, она построена как открытая система и предоставляет возможность каждому желающему получить доступ к своим программным кодам и внести в них изменения, добавив новые функции, типы данных или просто настроить систему «под себя». Поддержку системы обеспечивает консорциум Scilab, в состав которого входят больше двадцати участников, в том числе французские компании Mandriva, INRIA и ENPC.
Далее рассматривается версия системы для Windows 5.3.3. Эта версия содержит в своем составе дополнения ATOMS (AutomaTic mOdules Management for Scilab) для управления внешними модулями и Xcos для моделирования и эмуляции гибридных динамических систем. Упреждая вопросы и комментарии, замечу, что имеется версия и для Linux.
Понятие «вектор», «матрица», «массив»
Форма представления данных в Scilab является табличной. Это дает возможность решать разные задачи, связанные с инженерно-техническими вычислениями (особенно там, где используются матрицы и векторы) с очень высокой скоростью. В свою очередь, достаточно часто и в математике приходится работать с данными, представленными в виде таблиц. Например, при помощи табличного представления данных удобно решать системы линейных уравнений. Для лучшего понимания дальнейшего материала считаю целесообразным напомнить математические понятия вектора и матрицы.
Матрицу можно рассматривать как совокупность нескольких векторов одинаковой длины, например, М= 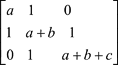
Учитывая важность табличного представления данных, все популярные математические системы (кстати, как и все алгоритмические языки) имеют особый тип данных для работы с векторами и матрицами: одномерные (для работы с векторами) и двумерные (для работы с матрицами) массивы. Впрочем, одномерные массивы можно рассматривать как частный случай (когда одна из размерностей равняется единице) двумерных. Массивом в математических системах называют данные особого типа, которые являются совокупностью конечного числа однотипных (например, числовых) элементов с уникальным именем. В дальнейшем термин «массив» используется как обобщающее название векторов и матриц.
Интерфейс системы
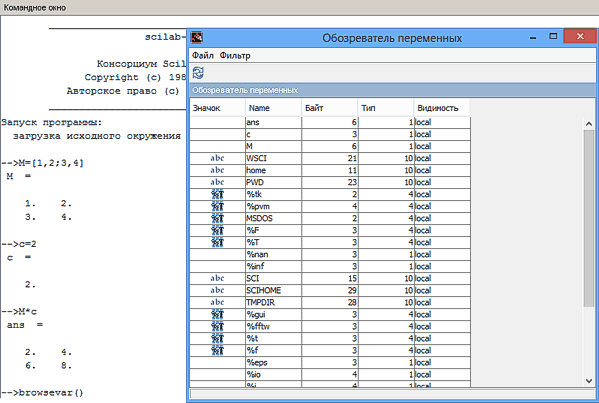
Окно команд (Command Window)
Для очистки окна команд следует выполнить команду Clc, нажать функциональную клавишу или выполнить команду Настройки > Очистить командное окно.
Окно пересмотра переменных (BrowseVar)
Сессия
Сеанс работы с системой называют сессией. Сессия, по сути, является текущим документом, содержащим работу пользователя с системой: строки ввода, вывода, сообщения об ошибках. Определение переменных и функций, которые расположены в рабочей области памяти, (но не саму сессию!) можно записать на диск командою Файл > Сохранить окружение. Файл хранится с расширением BIN. Следует отметить, что возможности сохранения всего текста сессии команда Сохранить окружение не дает. Это сделано преднамеренно: сессия является результатом проб и ошибок, ее текст вместе с правильными операциями может содержать сообщения об ошибках, ненужные выводы и т.п. Необходимости хранить все это, как правило, нет. Однако это не значит, что вообще отсутствует возможность запомнить адекватную часть расчетов. Для этого следует воспользоваться редактором и отладчиком, которые позволяют (после отладки расчета) получить документ в корректной форме без синтаксических и других ошибок. Загрузка с диска данных рабочей области происходит командою Файл > Загрузить окружение. Если все же есть необходимость полностью сохранить сессию, то это можно сделать при помощи команды diary, которая предназначена для ведения дневника сессии. Команда имеет два формата, при помощи которых начинается и прекращается процесс записи сессии:
По умолчанию система после загрузки ищет документы в системной папке Documents and Setting/Имя пользователя. Для изменения местоположения папки с документами следует выполнить команду Файл > Сменить текущий каталог или на панели инструментов щелкнуть кнопку 
После формирования сценария пользователь может загрузить его в Scilab, то есть выполнить его. Однако, понятно, что сценарий создается для многократного выполнения, потому после отладки программы-расчета ее сохраняют на диске, откуда она может быть в любой момент загружена в сессию Scilab. Это осуществляется командою Файл > Сохранить как. Файл сценария создается с расширением SCE.
Загрузка сценария в сессию Scilab осуществляется командой Файл > Выполнить.
Но вовсе не обязательно создавать сценарий. Любые вычисления (временами достаточно сложные) в системе можно выполнить в режиме прямых вычислений, то есть без подготовки программы. Это превращает Scilab в мощный калькулятор, способный осуществлять не только обычные для калькуляторов вычисления (например, выполнять арифметические операции и вычислять элементарные функции), но и осуществлять операции с векторами и матрицами, комплексными числами, рядами и полиномами, решать системы линейных уравнений и т.д.
Для использования системы в режиме прямых вычислений нужно знать, как именно вводится информация.
Правила ввода информации в документ
Обращение к справочной системе производится командой Справка > Содержание или щелчком кнопки 
Система содержит библиотеку демонстрационных примеров (необходимость ее установки на компьютере пользователя определяется во время инсталляции системы). Обращение к ней происходит командою Справка > Примеры. Демонстрационные примеры открываются в новом окне, которое нужно закрывать по окончанию пересмотра примера.