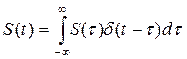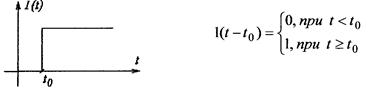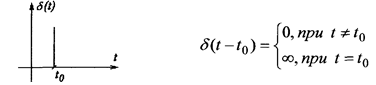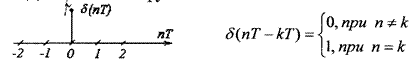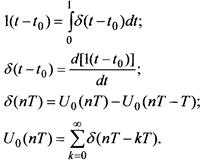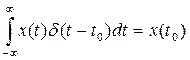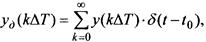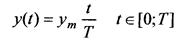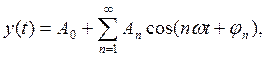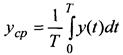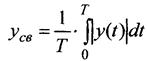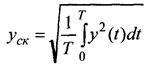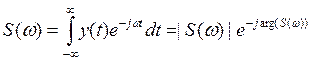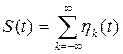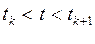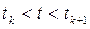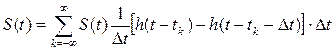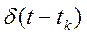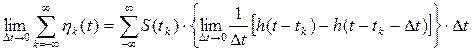сигнал параметры которого в следующий момент времени известны называется
Детерминированный сигнал
4. Детерминированный сигнал
Сигнал, мгновенные значения которого в любой момент времени известны.
Примечание. Общие характеристики детерминированного сигнала могут быть найдены расчетным путем
Полезное
Смотреть что такое «Детерминированный сигнал» в других словарях:
детерминированный сигнал — Сигнал, мгновенные значения которого в любой момент времени известны. Примечание Общие характеристики детерминированного сигнала могут быть найдены расчетным путем. [ГОСТ 16465 70] Тематики телевидение, радиовещание, видео Обобщающие термины… … Справочник технического переводчика
Детерминированный сигнал — 1. Сигнал, мгновенные значения которого в любой момент времени известны Употребляется в документе: Приложение № 6 ГОСТ 16465 70 Сигналы радиотехнические измерительные. Термины и определения … Телекоммуникационный словарь
Сигнал (техника) — Сигнал в теории информации и связи называется материальный носитель информации, используемый для передачи сообщений по системе связи. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым… … Википедия
Сигнал — У этого термина существуют и другие значения, см. Сигнал (значения). Эта статья или раздел нуждается в переработке. Пожалуйста, улучшит … Википедия
Детерминированный автомат — математическая модель системы, состояния которой меняются в дискретные моменты времени, причём каждое состояние системы полностью определяется предыдущим состоянием и входным сигналом. Д. а. формально описывается в виде функции f (si, aj) … Большая советская энциклопедия
импульсный сигнал — импульс Детерминированный сигнал конечной энергии, существенно отличный от нуля в течение ограниченного интервала времени, соизмеримого с временем установления переходного процесса в системе, для воздействия на которую этот сигнал предназначен.… … Справочник технического переводчика
Импульсный сигнал — 5. Импульсный сигнал Импульс Детерминированный сигнал конечной энергии, существенно отличный от нуля в течение ограниченного интервала времени, соизмеримого с временем установления переходного процесса в системе, для воздействия на которую этот… … Словарь-справочник терминов нормативно-технической документации
Импульсный сигнал — 1. Детерминированный сигнал конечной энергии, существенно отличный от нуля в течение ограниченного интервала времени, соизмеримого с временем установления переходного процесса в системе, для воздействия на которую этот сигнал предназначен… … Телекоммуникационный словарь
периодический сигнал — Детерминированный сигнал, мгновенные значения которого повторяются через равные промежутки времени. x(t) = x(t iT), где i любое целое число [ГОСТ 16465 70] Тематики телевидение, радиовещание, видео Обобщающие термины классификация измерительных… … Справочник технического переводчика
Периодический сигнал — 6. Периодический сигнал Детерминированный сигнал, мгновенные значения которого повторяются через равные промежутки времени x(t) = x(t iT), где i любое целое число Источник: ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины и… … Словарь-справочник терминов нормативно-технической документации
Виды сигналов, модуляция
Аналоговая величина – величина, значения которой в заданном интервале изменяются непрерывно. Её конкретное значение зависит только от точности прибора, производящего измерения. Это, например, температура.
Дискретная величина – величина, значения которой изменяются скачкообразно. Например, число студентов в аудитории. Измерительный сигнал – сигнал, содержащий количественную информацию об измеряемой физической величине. Например, напряжение на выходе термоэлектрического преобразователя, измеряющего температуру.
Сигнал данных – форма представления сообщения данных с помощью физической величины, изменения одного или нескольких параметров которой, отображает его изменение.
В микропроцессорной технике сигналами являются электрические величины (ток, напряжение). Представляющий параметр сигнала данных – параметр сигнала данных, изменение которого отображает изменение сообщения данных (амплитуда, частота, фаза, длительность импульса, длительность паузы).
Аналоговый сигнал данных – сигнал данных, у которого каждый из представляющих параметров описывается функцией времени и непрерывным множеством возможных значений, т.е. аналоговые сигналы описываются непрерывной (или кусочно-непрерывной) функцией xa(t), причём сама функция и аргумент t могут принимать любые значения на некоторых интервалах
Аналоговый сигнал f (t) называется периодическим, если существует действительное число T, такое, что f (t + T) = f (t) для любых t, при этом T называется периодом сигнала.
Сама функция xд (nT) может в дискретные моменты принимать произвольные значения на некотором интервале. Эти значения функции называются выборками или отсчётами функции. Другим обозначением решётчатой функции x(nT) является x(n) или xn. Последовательность x(n) может быть конечной или бесконечной, в зависимости от интервала определения функции.
Квантованный сигнал данных – отличается от аналоговых или дискретных разбиением диапазона значений непрерывной или дискретной величины на конечное число интервалов. Простейшим видом квантования является деление целочисленного значения на натуральное число, называемое коэффициентом квантования.
Цифровой сигнал данных – сигнал, у которого каждый из представляющих параметров описывается функцией дискретного времени и конечным множеством возможных значений. Цифровые сигналы описываются квантованными решётчатыми функциями xц(nT). При получении цифрового сигнала из аналогового происходят дискретизация и квантование.
Двоичный цифровой сигнал – сигнал данных, в котором используется способ представления информации о величине параметра в виде многоразрядной комбинации двух величин – нуля и единицы – и называемый обычно двоичным кодом.
В двоичном коде используются только две цифры: 1 и 0. Любое число содержит некоторое количество разрядов, в каждом из которых может стоять только одна из этих цифр. Одна цифра соответствует одному состоянию какого-либо элемента, например, замкнутому контакту, а другая — другому состоянию элемента — разомкнутому контакту.
Модуляция – процесс изменения одного или нескольких параметров высокочастотного несущего колебания по закону низкочастотного информационного сигнала (сообщения).
В наше время двоичные цифровые сигналы в связи с простотой кодирования и обработки используются в цифровых электронных устройствах. Для передачи цифрового сигнала по каналам связи (например, электрическим или радиоканалам) используются различные виды модуляции.
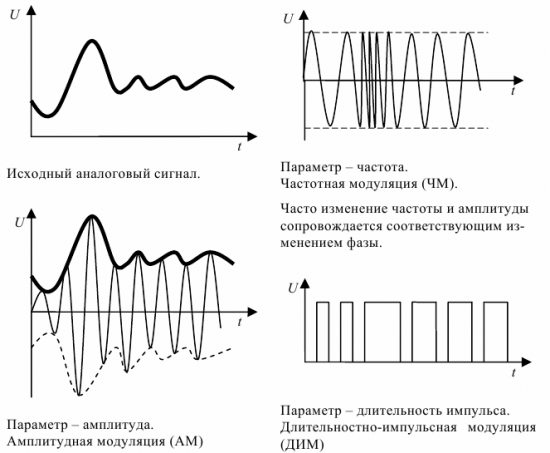
Рассмотрим примеры представляющих параметров сигналов данных на примере различных видов модуляции (см. рис. 1). Кроме рассмотренных видов модуляции, также существуют фазовая (ФМ), время-импульсная (ВИМ), широтно-импульсная (ШИМ) и другие модуляции.
Рис. 1. Различные виды модуляции сигналов – различные представляющие параметры сигналов данных
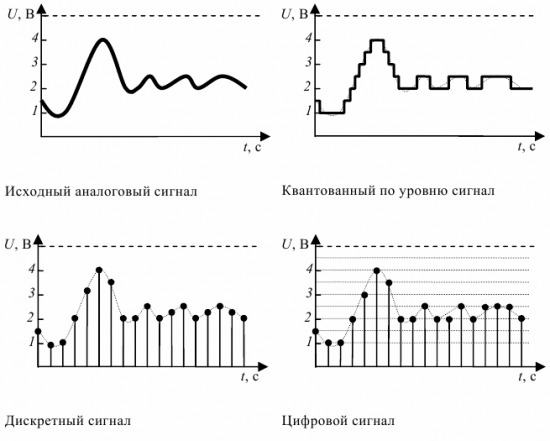
Для понимания сущности цифрового сигнала рассмотрим следующую классификацию. В цифровой технике выделяют сигналы (рис. 2):
произвольные по величине и непрерывные во времени (аналоговые);
произвольные по величине и дискретные по времени (дискретные);
квантованные по величине и непрерывные по времени (квантованные);
квантованные по величине и дискретные по времени (цифровые).
Рис. 2. Аналоговый, дискретный, квантованный и цифровой сигналы
Аналоговые сигналы часто используют для представления непрерывно изменяющихся физических величин. Например, аналоговый электрический сигнал, снимаемый с термопары, несёт информацию об изменении температуры, сигнал с микрофона – о быстрых изменениях давления в звуковой волне и т.п.
В области цифровой и импульсной техники терминология не является установившейся. Так, дискретный сигнал – это сигнал, значения представляющего параметра которого известны только в определённые моменты времени, а также это сигнал, в отличие от аналогового, представляющий параметр которого может принимать только фиксированные значения (обычно два: логический «ноль» или логическую «единицу»).
Во втором случае было бы правильно называть сигнал квантованным, но промышленные модули называются «модулями ввода дискретных сигналов». Кроме использования для передачи информации различных физических величин, сигналы различаются также представляющими параметрами.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Аналоговые, дискретные и цифровые сигналы
Любая физическая величина по характеру изменения ее значения может быть постоянной (если она имеет только одно фиксированное значение), дискретной (если она может иметь два или более фиксированных значений), или аналоговой (если она может иметь бесчисленное множество значений). Все эти величины могут быть преобразованы в цифровую форму.
Аналоговым называется такой сигнал, который может быть представлен непрерывной линией из множества значений, определенных в каждый момент времени относительно временной оси. Значения аналогового сигнала произвольны в каждый момент времени, поэтому он может быть в принципе представлен как некая непрерывная функция (зависящая от времени как от переменной) либо как кусочно-непрерывная функция времени.
Аналоговым сигналом можно назвать, например, звуковой сигнал, генерируемый обмоткой электромагнитного микрофона или ламповым акустическим усилителем, поскольку такой сигнал непрерывен и его значения (напряжение или ток) сильно отличаются друг от друга в каждый момент времени.
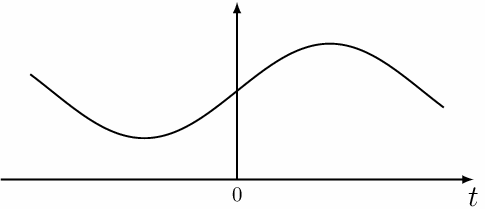
На приведенном ниже рисунке изображен пример подобного рода аналогового сигнала.
Аналоговые величины могу иметь бесконечное множество значений в определенных пределах. Они непрерывны и их значения не могут изменяться скачками.
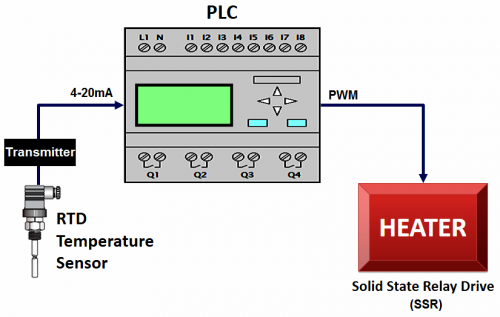
Пример аналогового сигнала: термопара передает в аналоговом виде значение температуры в программируемый логический контроллер, который управляет с помощью твердотельного реле температурой в электрической печи.
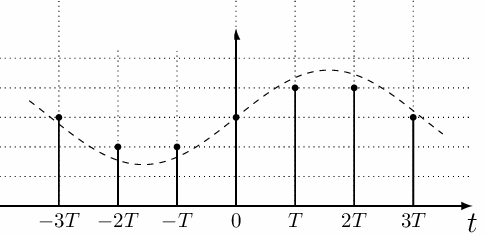
Если некий сигнал принимает произвольные значения лишь в отдельные моменты времени, то такой сигнал называют дискретным. Чаще всего на практике применяются дискретные сигналы, распределенные по равномерной временной решетке, шаг которой называется интервалом дискретизации.
Дискретный сигнал принимает определенные не нулевые значения лишь в моменты дискретизации, то есть он является не непрерывным в отличие от аналогового сигнала. Если из звукового сигнала вырезать небольшие кусочки определенного размера через равные интервалы, такой сигнал можно будет назвать дискретным.
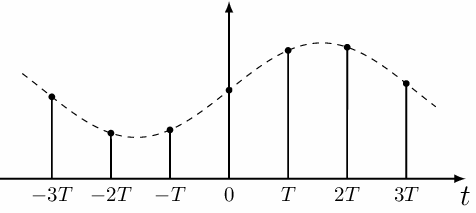
Ниже приведен пример формирования подобного дискретного сигнала с интервалом дискретизации Т. Обратите внимание, что квантуется лишь интервал дискретизации, но не сами значения сигнала.
Дискретные сигналы имеют два и более фиксированных значений (количество их значений всегда выражается целыми числами).
Когда дискретный сигнал принимает только какие-то фиксированные значения (которые могут быть расположены по сетке с определенным шагом), такие что они могут быть представлены как количество квантовых величин, такой дискретный сигнал называется цифровым. То есть цифровой сигнал — это такой дискретный сигнал, который квантован не только по промежуткам времени, но и по уровню.
Практически дискретные и цифровые сигналы в ряде задач отождествляются, и могут быть легко заданы в форме отсчетов с помощью вычислительного устройства.
На рисунке приведен пример формирования цифрового сигнала на базе аналогового. Обратите внимание, что значения цифрового сигнала не могут принимать промежуточных значений, а только определенные — целое количество вертикальных шагов сетки.
Цифровой сигнал легко записывается и перезаписывается в память вычислительных устройств, просто считывается и копируется без потери точности, тогда как перезапись аналогового сигнала всегда сопряжена с утратой некоторой, пусть и незначительной, части информации.
Обработка цифровых сигналов позволяет получать устройства с очень высокими характеристиками благодаря выполнению вычислительных операций совершенно без потерь качества, либо с пренебрежимо малыми потерями.
В силу этих достоинств, именно цифровые сигналы повсеместно распространены сегодня в системах хранения и обработки данных. Вся современная память — цифровая. Аналоговые носители информации (такие как пленочные кассеты и т.д.) давно ушли в прошлое.
Аналоговый и цифровой приборы для измерения напряжения:
Но даже у цифровых сигналов есть свои недостатки. Их невозможно передать напрямую как есть, ибо передача обычно реализуется посредством непрерывных электромагнитных волн. Поэтому при передаче и приеме цифровых сигналов необходимо прибегать к дополнительной модуляции и аналого-цифровому преобразованию. Меньший динамический диапазон цифровых сигналов (отношение наибольшего значения к наименьшему), обусловленный квантованностью значений по сетке, является еще одним их недостатком.
Существуют и такие области, где аналоговые сигналы незаменимы. Например аналоговый звук никогда не сравнится с цифровым, поэтому ламповые усилители и пластинки до сих пор не выходят из моды, несмотря на обилие цифровых форматов записи звука с самой высокой частотой дискретизации.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Сигналы и спектры. Основные понятия – ЧАСТЬ 1
В телекоммуникациях под сигналом понимают физический процесс, который отображает реализацию информационного сообщения в форме, удобной для передачи, обработки и восприятия. Понятие «сигнал» имеет взаимосвязь с понятиями «данные» (data) и «информация» (information), хотя все они относятся к разным семантическим категориям. По существу, сигналы являются физической формой представления информации и данных.
В телекоммуникациях наиболее распространенной формой представления сигналов является электрическая форма, которая отображает функциональную зависимость напряжения от времени U(t). Такое математическое представление сигналов позволяет проводить их классификацию и сравнение.
В беспроводной связи сигналы, описываемые математическими моделями, по критерию информативности разделяют на детерминированные и случайные. Детерминированным сигналом называется сигнал, значения которого в любые моменты времени являются известными величинами. Значения параметров случайных сигналов заранее не известны и могут определяться лишь с некоторой степенью вероятности [2]. Классическим примером детерминированного сигнала может служить гармонический сигнал, математическая модель которого имеет вид:
Примером случайного сигнала может служить любая помеха – ее параметры заранее не известны.
Детерминированные сигналы, в свою очередь, делятся на две категории: периодические и непериодические. Периодический сигнал повторяется через определенные промежутки времени, в то время как непериодический сигнал не повторяется при равных условиях [2]. Последние делятся по форме на аналоговые и дискретные. Аналоговый сигнал по своим значениям является непрерывной функцией, определенной для каждого значения аргумента. При этом значение функции в каждый момент времени можно предсказать с большой точностью. Математическая функция, описывающая дискретный сигнал, также является непрерывной по своим значениям, но определяется только по дискретным значениям аргумента. Дискретный сигнал, квантованный по амплитуде, называют цифровым. Значения параметров цифрового сигнала можно привязать к конкретной системе счисления и обрабатывать числовыми методами [2]. Все современные системы мобильной связи и беспроводного доступа являются цифровыми, поэтому в дальнейшем цифровым сигналам и их цифровой обраоо!ке уделяется основное внимание.
Форма представления сигналов, которая соответствует их математическому описанию в виде функций независимых аргументов, называется динамической. Кроме этой традиционной формы представления сигналов, используют форму их математического описания с помощью т.н. обратных аргументов (например, обратным аргументом для времени t является частота У). Эту форму называют спектральной. Возможность подобного представления обусловлена свойствами динамического описания сигналов, благодаря которым любой сложный сигнал можно записать в виде суммы возникающих в последовательные моменты времени элементарных сигналов (т.е. разложить на гармонические составляющие). Если длительность этих элементарных сигналов устремить к нулю, в пределе получим точное представление сигнала. Это разложение описывается функциями значений амплитуд и начальных фаз колебаний по непрерывному или дискретному аргументу, в качестве которого выступает частота изменения функций на интервалах их представления. Совокупность амплитуд элементарных сигналов разложения называют амплитудным спектром сигнала, а совокупность фаз – фазовым спектром сигнала. Вместе эти два спектра образуют частотный спектр сигнала [2].
Если известна форма сигнала (зависимость значения функции от значения аргумента), спектр может быть рассчитан при помощи преобразования Фурье. Другими словами, периодическую функцию, заданную на интервале ее периода Т, которая является ограниченной и кусочно-непрерывной с конечным числом разрывов 1-го рода (условие Дирихле), можно представить в виде ряда Фурье [2]:
где S – т.н. весовые коэффициенты ряда.
Первую частотную составляющую дискретного спектра (при п= 1) называют основной (центральной) частотой сигнала, а другие частоты – гармониками. Для построения спекгра непериодического сигнала используется т.н. интегральное преобразование Фурье [2].
Рис. 2.1. Форма прямоугольного видеоимпульса, его энергетический спектр и спектр прямоугольного радиоимпульса
Подход к определению корреляционных характеристик периодических лов несколько иной. В этом случае АКФ вычисляется путем усреднения скал СИГНа произведения сигнала и его сдвигаемой копии в пределах одного периода Т[3]- 0Г °
В этом случае АКФ является Фурье-образом спектральной плотности м ности, а ее значение в нуле равно средней мощности сигнала [3].
Лекция №3. Сигнал— материальный носитель информации, представляющий собой некий физический процесс, один из параметров которого непосредственно связан с измеряемой



Сигнал— материальный носитель информации, представляющий собой некий физический процесс, один из параметров которого непосредственно связан с измеряемой физической величиной. Этот параметр называется информативным.
КЛАССИФИКАЦИЯ СИГНАЛОВ
Измерительный сигнал— сигнал, который обязательно дает количественную оценку измеряемой физической величине.
«Сигналы технической радиоэлектронной теории» Классификация измерительных сигналов (ИС):
1.По характеру измерения во времени, может быть:
■ Постоянный сигнал— сигнал, который не изменяется во времени.
■ Переменный сигнал.В свою очередь который подразделяется на непрерывный
и импульсный (колебания, действующие определенный конечный отрезок времени). Примером может служить радио и импульсы.
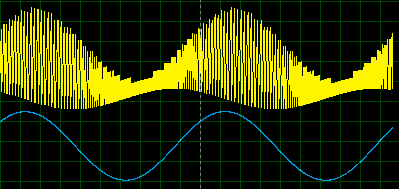
Жирным выделена видимая часть Ue(t). Up(t)=Ue(t)cos((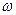
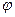
2. По характеру измерения информационного и временного параметра подразделяются на:
■ Аналоговый— сигнал, описывающийся непрерывной или кусочно-непрерывной функцией.
■ Дискретный сигнал— сигнал, изменяющийся дискретно по времени.
Описывается решетчатыми функциями.
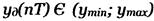
■ Квантовые сигналы— сигналы, квантованные по уровню.
■ Цифровой сигнал— сигнал квантования по уровню и дискретизированный по времени.
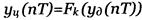
Для цифровых сигналов удобна система представления фиксированных значений в виде чисел. (Например: двоичная система исчисления). Для восьмиуровневого квантования необходим трёхразрядный двоичный код).
Число уровней квантования N и наименьшее число разрядов m двоичных чисел:
С уменьшением кванта 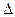
3. По степени наличия априорной информации о характере изменения ИС:
■ Детерминированные сигналы— определенные. Сигналы, мгновенное значение которых можно предсказать в любой момент времени.
■ Квадетерминированные— с частично известными параметрами.
■ Случайный— сигнал, поведение которого предсказать невозможно.
Виды детерминированных сигналов:
Элементарные — тестовые сигналы. Предназначены для анализа и проверки радиотехнических устройств (к ним относятся элементарные и ряд сложных).
Временные представления элементарных функций:
•Единичная функция. Функция Хевисайда
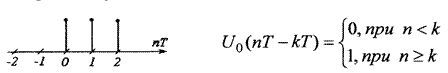
•Дискётная S – функция:
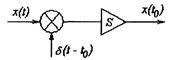
Стробируянепрерывный сигнал, мы получаем дискретный. Процесс стробирования записывается:
Согласно уравнению: если непрерывную функцию умножить на 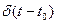
Структурная модель выглядит следующим образом:
Идеальный дискретный сигнал:
y(t)=ymsin(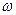
Сложные сигналы:
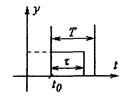
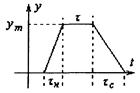
y(t)=ym[1-(t-to)-1-(t-to-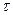
где 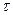
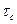
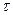
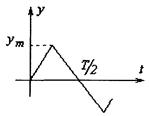
К сложным измерительным сигналам относится любой модулированный сигнал.
Говоря о детерминированных сигналах, их подразделяют на периодические и непериодические.
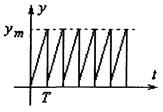
Периодические сигналы:
Периодический сигнал часто характеризуется спектром, используя преобразование Фурье.
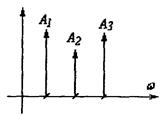
Линейчатый амплитудный спектр выглядит следующим образом:
Интегральные параметры:
· Среднее значение постоянной составляющей:
· Среднеквадратичное (действительное) значение:
Непериодические сигналы:
|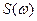
4. По размерности подразделяются:
■ Одномерный сигнал x(t);
■ Многомерный сигнал V(x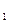
Основные способы описания сигналов:
1)представление в функции времени x(t),
2)представление в операторной форме x(p),
3)представление в виде функции частоты x(w),
4)представление в виде совокупности сигналов.
Принцип динамического представления сигнала – реальный сигнал представляется суммой элементарных сигналов, возникающих в последовательные моменты времени. Если длительность отдельных сигналов ® 0, то в пределе получим точное описание исходного сигнала.
К элементарным относят единичный импульс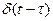
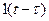
единичный импульс (d-функция) 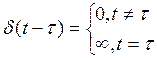
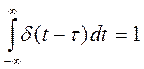
d-функция- математическая модель короткого внешнего воздействия с единичной площадью. Это идеализированный сигнал, характеризуемый малой длительностью, с ¥ уровнем, площадью, равной единице.
2) 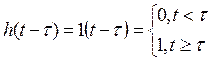
|
|
|
Динамическое представление сигнала посредством d-функции
Принцип динамического представления сигнала – реальный сигнал представляется суммой элементарных сигналов, возникающих в последовательные моменты времени. Если длительность отдельных сигналов ® 0, то в пределе получим точное описание исходного сигнала.
Существует два способа динамического представления (ДП)
1)ступенчатой функцией через равные промежутки времени Δ.





Опишем аналоговый сигнал суммой примыкающих друг к другу прямоугольных импульсов.




если SK— значение сигнала на K-ом отсчете, то элементарный импульс с номером K опишется во времени как
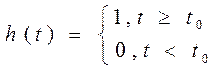
Исходный сигнал должен рассматриваться как сумма элементарных сигналов в соответствии с принципами динамического представления сигналов
в этой å отличен от нуля один член соответствующий 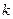
h(t) – скачкообразная функция, функция Хевисайда (включения)
Переходим к пределу, Dt®0,
 |