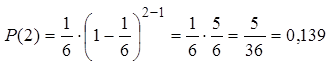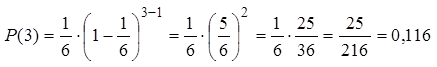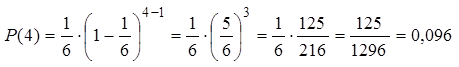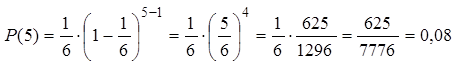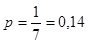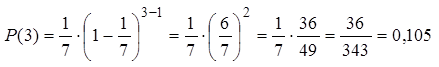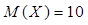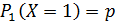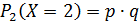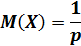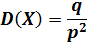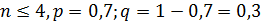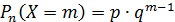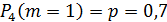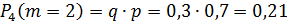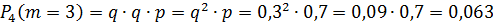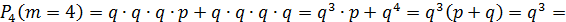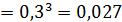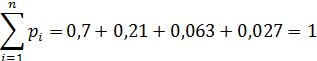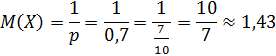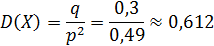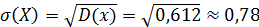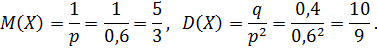случайная величина имеет геометрическое распределение с параметром

Геометрическое распределение

Содержание:

Вероятности для значений I, 2. образуют геометрическую прогрессию с первым членом р и знаменателем q, поэтому такое распределение называют геометрическим.

В последовательности независимых испытаний Бернулли (р — вероятность успеха в каждом испытании, q — вероятность неуспеха) рассмотрим случайную величину X — номер испытания, являющегося первым успехом. По смыслу X — ДСВ, так как множество реальных значений X является счетным множеством.

Проверим нормировку ряда:

так как ряд представляет собой убывающую геометрическую прогрессию. Поэтому это распределение называется геометрическим. Вычислим основные характеристики ДСВ X.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Возможно вам будут полезны данные страницы:

Пример с решением №1

Студент подготовил из 40 экзаменационных билетов 32 и мечтает, что преподаватель разрешит ему выбрать выученный билет. Составить ряд распределений числа X возможных попыток взять билет до появления первого «знакомого» билета, если преподаватель остановил студента после четвертой попытки. Найти числовые характеристики этой случайной величины.

Решение:

Вероятность того, что студент возьмет выученный билет, равна 0,8. Случайная величина X — число испытаний до появления первого выученного билета. Составим ряд распределений, найдем функцию распределения ДСВ X, построим ее график. Найдем все числовые характеристики (ограничиться тремя-пятью испытаниями).

Обозначим через — число «испытаний», через р — вероятность взять выученный билет. Тогда Найдем вероятности

Так как случайная величина X — число возможных попыток до появления первого выученного билета, воспользуемся геометрической вероятностью:

Математическое ожидание

дисперсия

среднеквадратическое отклонение

Почему в рассмотренной задаче не выполняется условие нормировки:

Дело в том, что в случае геометрических распределений условие нормировки выполняется при а в рассмотренной задаче были даны лишь четыре первые значения ДСВ X.

Геометрическое распределение

Определение. Дискретная случайная величина имеет геометрическое распределение с параметром р, если она принимает значения 1,2. (бесконечное, но счетное множество значений) с вероятностями где

Ряд геометрического распределения случайной величины имеет вид:

Нетрудно видеть, что вероятности образуют геометрическую прогрессию с первым членом и знаменателем q (отсюда название «геометрическое распределение»).

Определение геометрического распределения корректно, так как сумма ряда

(так как есть сумма геометрического ряда при).

Случайная величина , имеющая геометрическое распределение, представляет собой число испытаний, проведенных по схеме Бернулли, с вероятностью р наступления события в каждом испытании до первого положительного исхода.

Теорема. Математическое ожидание случайной величины X, имеющей геометрическое распределение с параметром р,

а ее дисперсия 1 где

Пример с решением №2

Проводится проверка большой партии деталей до обнаружения бракованной (без ограничения числа проверенных деталей). Составить закон распределения числа проверенных деталей. Найти его математическое ожидание и дисперсию, если известно, что вероятность брака для каждой детали равна 0,1.

Решение:

Случайная величина X — число проверенных деталей до обнаружения бракованной — имеет геометрическое распределение (4.11) с параметром р =0,1. Поэтому ряд распределения имеет вид

Гипергеометрическое распределение

Определение. Дискретная случайная величина X имеет гипергеометрическое распределение с параметрами если она принимает значения 1 0, 1, 2, с вероятностями

где — натуральные числа.

Гипергеометрическое распределение имеет случайная величина — число объектов, обладающих заданным свойством, среди объектов, случайно извлеченных (без возврата) из совокупности N объектов, М из которых обладают этим свойством.

Так, распределение случайной величины X — числа неточных приборов среди взятых наудачу четырех, полученное в примере 3.20, есть гипергеометрическое распределение с параметрами

Теорема. Математическое ожидание случайной величины X, имеющей гипергеометрическое распределение с параметрами , М, N, есть

а ее дисперсия Случайную величину , распределенную по биномиальному закону (4.1), можно интерпретировать как число объектов, обладающих данным свойством, из общего числа объектов, случайно извлеченных из некоторой воображаемой бесконечной совокупности, доля р объектов которой обладает этим свойством. Поэтому гипергеометрическое распределение можно рассматривать как модификацию биномиального распределения для случая конечной совокупности, состоящей из N объектов, М из которых обладают этим свойством.

Можно показать, что при функция вероятностей (4.14) гипергеометрического распределения стремится к соответствующей функции (4.1) биномиального закона.

Гипергеометрическое распределение широко используется в практике статистического приемочного контроля качества промышленной продукции, в задачах, связанных с организацией выборочных обследований, и других областях.

Пример с решением №3

В лотерее «Спортлото 6 из 45» денежные призы получают участники, угадавшие 3, 4, 5 и 6 видов спорта из отобранных случайно 6 видов из 45 (размер приза увеличивается с увеличением числа угаданных видов спорта). Найти закон распределения случайной величины X — числа угаданных видов спорта среди случайно отобранных шести. Какова вероятность получения денежного приза? Найти математическое ожидание и дисперсию случайной величины X.

Решение:

Очевидно (см. гл. 1, пример 1.14), что число угаданных видов спорта в лотерее «6 из 45» есть случайная величина, имеющая гипергеометрическое распределение с параметрами . Ряд ее распределения, рассчитанный по формуле (4.14), имеет вид:

Вероятность получения денежного приза По формулам (4.15) и (4.16)

Таким образом, среднее число угаданных видов спорта из 6 всего 0,8, а вероятность выигрыша только 0,024. ►

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Геометрическое распределение

Геометрическое распределение (Фарри). Это закон распределения дискретной случайной величины, связанный с последовательностью независимых испытаний, при этом случайной величиной является число проведённых испытаний до первого осуществления наблюдаемого события.

ü число выстрелов до первого попадания в цель;

ü число проверенных изделий до первого появления бракованного изделия;

ü число подбрасываний кубика до выпадения шести очков и т.п.

(14)

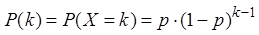
Замечание: при любом значении p, не равном нулю или единице, наивероятнейшим значением является единица. C ростом k вероятности монотонно убывают.

Вероятности 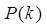для последовательных значений k образуют геометрическую прогрессию с первым членом р и знаменателем (1-p), откуда и название «геометрическое распределение».

Основные числовые характеристики геометрического распределения:

1) математическое ожидание

(15)

(16)

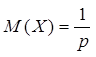
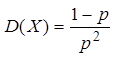
Пример 5: Кубик подбрасывается до тех пор, пока не выпадет 6 очков. Найти вероятность, что выпадение 6 очков случится за 5 бросков.

Для первого броска (k = 1), вероятность успеха p(1) = 1/6.

Для второго (k = 2) это вероятность успеха во втором броске и неудачи в первом по формуле (14):

для третьего броска:

для четвертого броска:

Ответ: вероятность, что выпадение 6 очков случится за 5 бросков равна 0,08.

Пример 6: Ролик кодового замка содержит 7 возможных цифр, из которых нужно выбрать одну. Какова вероятность, что его можно открыть точно с 3-го раза.

Вероятность правильного единичного выбора

Распределение геометрическое значит искомую вероятность найдем по формуле (14)

Если замок состоит из нескольких независимых роликов, то вероятность его случайного открывания подчиняется уже другому распределению – биномиальному.

Ответ: вероятность, что замок откроется точно с 3-го раза равна 0,105.

Пример 7: Контроль качества партии продукции проводится до обнаружения первого бракованного изделия. В результате серии проверок обнаружили, что бракованное изделие впервые появлялось в среднем при десятом испытании. Оценить вероятность появления брака.

Пусть Х – число испытаний до первого появления бракованного изделия. Х случайная величина имеет геометрическое распределение. По условию ее среднее значение равно

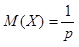
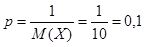
Так как , то .

Ответ: вероятность появления брака равна 0,1.

Источник

Геометрический закон распределения (геометрическое распределение) дискретных случайных величин.

Дискретная случайная величина распределена геометрически, если она принимает значения 1,2,…m …(бесконечное, но счетное количество раз) с вероятностями, находящимися по формуле общего члена геометрической прогрессии:

Случайная величина X = m, распределенная геометрически, представляет собой число испытаний (m) до первого положительного исхода.

Составим ряд распределения:

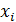	…	m	…
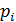	p		…		…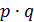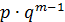

Теорема. Математическое ожидание и дисперсия случайной величины, распределенной геометрически, вычисляются по формулам:

Пример.

Охотник стреляет по дичи до первого попадания, но успевает сделать не более 4‒х выстрелов.

Составить закон распределения числа выстрелов, если вероятность попадания при одном выстреле равна p = 0,7.

Решение:

число выстрелов

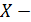
Составим закон распределения числа выстрелов:

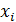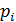	0,7	0,21	0,063	0,027

Проверка:

1. Математическое ожидание:

3. Среднее квадратическое откланение:

4. так как при m = 1 вероятность максимальная, она составляет

Пример.

Вероятность поражения цели равна 0,6. Производится стрельба по мишени до первого попадания (число патронов не ограничено). Требуется составить ряд распределения числа сделанных выстрелов, найти математическое ожидание и дисперсию этой случайной величины. Определить вероятность того, что для поражения цели потребуется не более трёх патронов.

Решение:

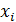	.	m	.
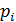	0,6	0,24	0,096	.	0,6·0,4m	.

Вероятность того, что для поражения цели потребуется не более трёх патронов равнаP(X≤3) = P(X=1) + P(X=2) + P(X=3) = 0,6+0,24+0,096 = 0,936.

Источник

Законы распределения дискретных случайных величин

Можно выделить наиболее часто встречающиеся законы распределения дискретных случайных величин:

Для данных распределений дискретных случайных величин расчет вероятностей их значений, а также числовых характеристик (математическое ожидание, дисперсия, и т.д.) производится по определенных «формулам». Поэтому очень важно знать данные типы распределений и их основные свойства.

1. Биномиальный закон распределения.

$\begin<|c|c|>
\hline
X_i & 0 & 1 & \dots & n \\
\hline
p_i & P_n\left(0\right) & P_n\left(1\right) & \dots & P_n\left(n\right) \\
\hline
\end$

2. Закон распределения Пуассона.

Пример. Примерами случайных величин, подчиненных закону распределения Пуассона, могут быть: число автомашин, которые будут обслужены завтра автозаправочной станцией; число бракованных изделий в произведенной продукции.

3. Геометрический закон распределения.

Пример. Примерами случайных величин, имеющих геометрическое распределение, могут быть: число выстрелов до первого попадания в цель; число испытаний прибора до первого отказа; число бросаний монеты до первого выпадения орла и т.д.

$\begin<|c|c|>
\hline
X_i & 1 & 2 & 3 & 4 \\
\hline
P\left(X_i\right) & 0,4 & 0,24 & 0,144 & 0,216 \\
\hline
\end$

$M\left(X\right)=\sum^n_=1\cdot 0,4+2\cdot 0,24+3\cdot 0,144+4\cdot 0,216=2,176.$

Среднее квадратическое отклонение:

4. Гипергеометрический закон распределения.

Пример. В кредитном отделе банка работают 5 специалистов с высшим финансовым образованием и 3 специалиста с высшим юридическим образованием. Руководство банка решило направить 3 специалистов Для повышения квалификации, отбирая их в случайном порядке.

а) Составьте ряд распределения числа специалистов с высшим финансовым образованием, которые могут быть направлены на повышение квалификации;

б) Найдите числовые характеристики этого распределения.

$\begin<|c|c|>
\hline
X_i & 0 & 1 & 2 & 3 \\
\hline
p_i & 0,018 & 0,268 & 0,536 & 0,179 \\
\hline
\end$

Источник