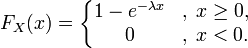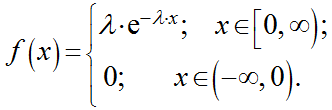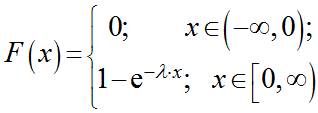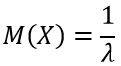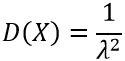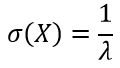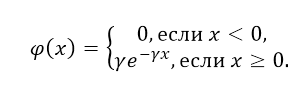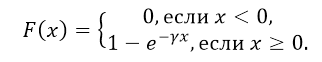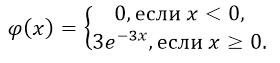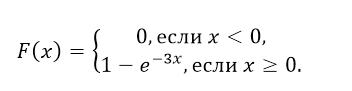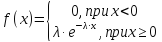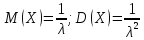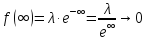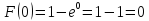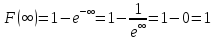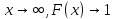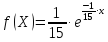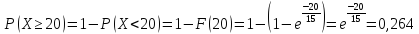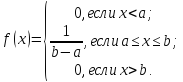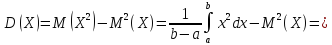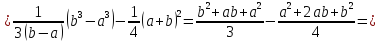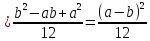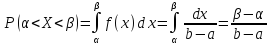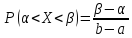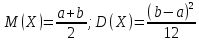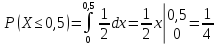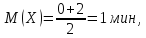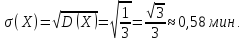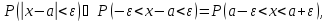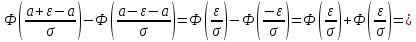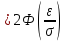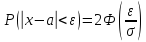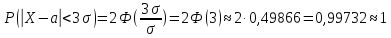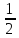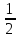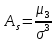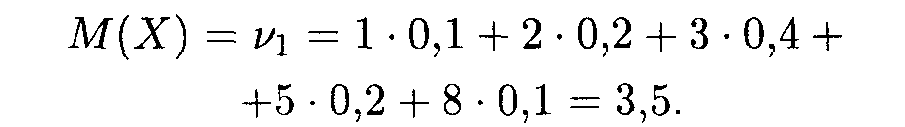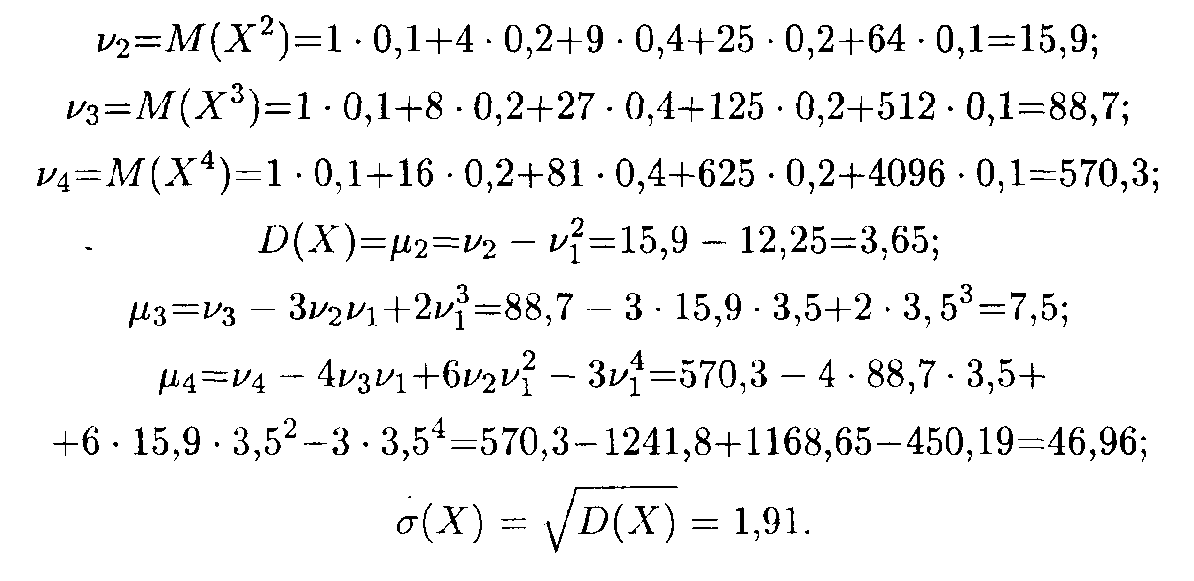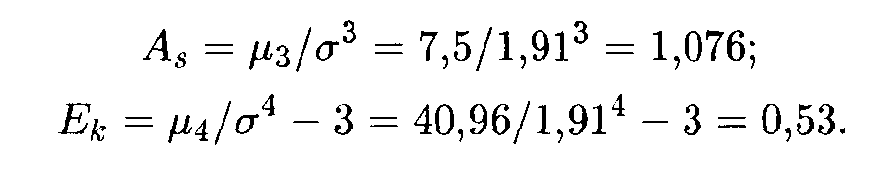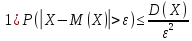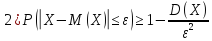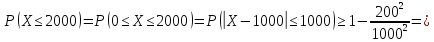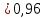случайная величина имеет показательное распределение с параметром

Показательное распределение

Показательное распределение

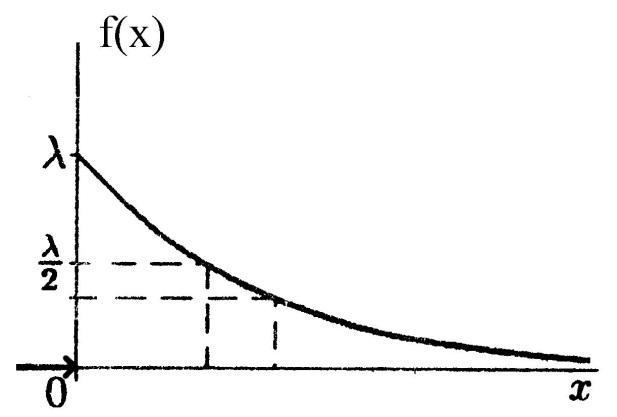
Плотность вероятности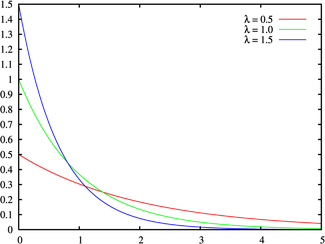
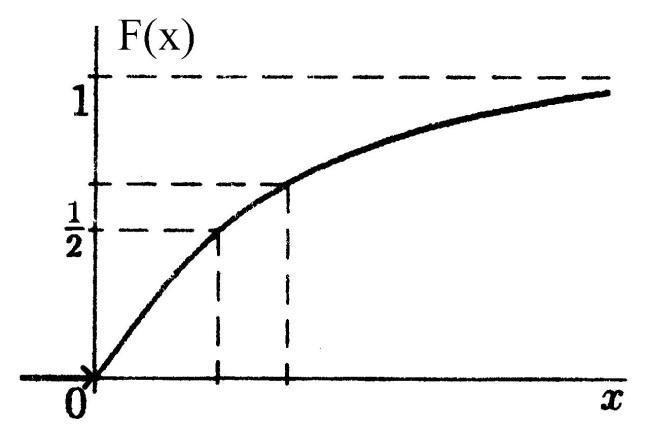
Функция распределения
Параметры	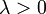— интенсивность или обратный коэффициент масштаба
Носитель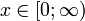
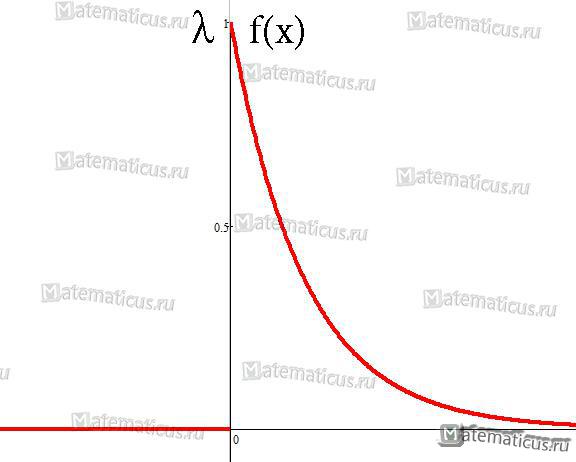
Плотность вероятности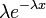
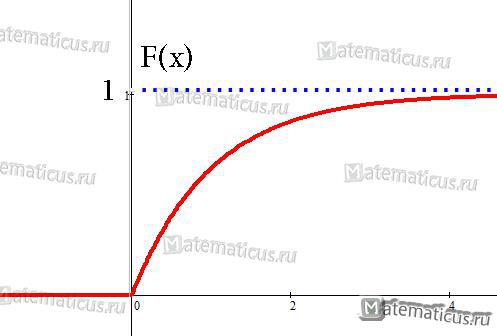
Функция распределения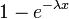
Математическое ожидание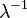
Медиана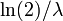
Мода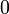
Дисперсия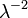
Коэффициент асимметрии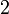
Коэффициент эксцесса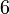
Информационная энтропия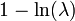
Производящая функция моментов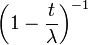
Характеристическая функция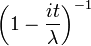

Показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

Содержание

Определение

.

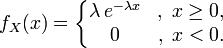
Иногда семейство экспоненциальных распределений параметризуют обратным параметром 1 / λ :

.

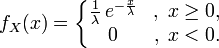
Оба способа одинаково естественны, и необходима лишь договорённость, какой из них используется.

В этой статье для определённости будем предполагать, что плотность экспоненциальной случайной величины X задана первым уравнением, и будем писать: .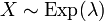

Функция распределения

Моменты

Несложным интегрированием находим, что производящая функция моментов для экспоненциального распределения имеет вид:

,

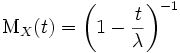
откуда получаем все моменты:

.

, .

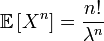
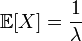
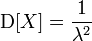
Отсутствие памяти

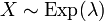
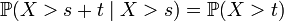
Пусть . Тогда .

Пример. Пусть автобусы приходят на остановку случайно, но с некоторой фиксированной средней интенсивностью. Тогда количество времени, уже затраченное пассажиром на ожидание автобуса, не влияет на время, которое ему ещё придётся прождать.

Связь с другими распределениями

Вероятностные распределения Одномерные Многомерные Дискретные: Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | равномерное мультиномиальное Абсолютно непрерывные: Бета | Вейбулла | Гамма | Колмогорова | Коши | Лапласа | логнормальное | Лоренца | нормальное (Гаусса) | равномерное | Парето | Стьюдента | Фишера | хи-квадрат | экспоненциальное | Эрланга многомерное нормальное

править

Полезное

Смотреть что такое «Показательное распределение» в других словарях:

показательное распределение — экспоненциальное распределение — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы экспоненциальное распределение EN exponential distribution … Справочник технического переводчика

Показательное распределение — распределение вероятностей на действительной прямой с плотностью вероятностей (См. Плотность вероятности) р (х), равной при х ≥ 0 показательной функции λe λx, λ > 0 [отсюда название П. р.] и при х … Большая советская энциклопедия

ОТРИЦАТЕЛЬНОЕ ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ — то же, что показательное распределение … Математическая энциклопедия

РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ — одно из основных понятий вероятностей теории и математической статистики. При современном подходе в качестве математич. модели изучаемого случайного явления берется соответствующее вероятностное пространство, где W множество элементарных … Математическая энциклопедия

Экспоненциальное распределение — Показательное распределение Плотность вероятности Функция распределения … Википедия

НЕПРЕРЫВНОЕ РАСПРЕДЕЛЕНИЕ — распределение вероятностей, не имеющее атомов. Если атомы суть отдельные точки, то Н. р. противоположно дискретному распределению (см. также Атомическое распределение). Вместе с дискретным распределением Н. р. образует основные типы распределений … Математическая энциклопедия

ЭРЛАНГА РАСПРЕДЕЛЕНИЕ — эрланговское распределение, сосредоточенное на распределение вероятностей с плотностью где целое и действительное параметры. Характеристич. функция Э. р. имеет вид а математич. ожидание и дисперсия соответственно и … Математическая энциклопедия

ЛАПЛАСА РАСПРЕДЕЛЕНИЕ — непрерывное распределение вероятностей с плотностью где параметр сдвига, а a>0, масштабный параметр. Плотность Л. р. симметрична относительно точки x=b, производная плотности имеет разрыв при x=b. Характеристич. функция Л. р. с параметрами a и … Математическая энциклопедия

ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ — то же, что показательное распределение … Математическая энциклопедия

Источник

Показательный (экспоненциальный) закон распределения

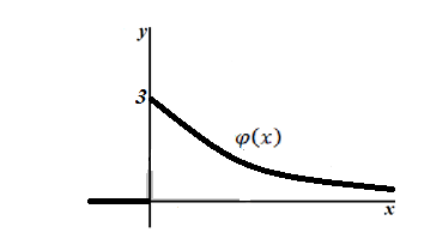
Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения, если её плотность вероятности имеет вид:

График плотности распределения случайной величины по показательному (экспоненциальному) закону

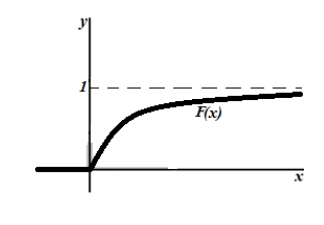
Функция распределения F(X) случайной величины X, распределенной по показательному закону, выражается формулой:

График функции распределения случайной величины по показательному (экспоненциальному) закону

λ — параметр распределения.

Математическое ожидание равно:

Дисперсия равна:

Среднеквадратическое отклонение (СКО) равно:

Вероятность того, что случайная величина X примет значение, принадлежащее интервалу (a, b), находится по формуле:

P(a −λa −e −λb

Показательное распределение применяют в теории массового обслуживания и надёжности, для моделирования времени безотказной работы, длительности безаварийной работы приборов и машин, демографии и т. д. Пример, устройство после включения ломается через короткий промежуток времени.

Случайная величина X – время работы лампы накаливания. Случайная величина подчинена показательному распределению. Определить вероятность того, что время работы лампы накаливания будет не меньше 800 часов, если среднее время работы лампы накаливания 400 часов.

В соответствии с условием задачи, математическое ожидание M(x) случайной величины X равно 400 часам, отсюда следует, что

Подставляя в формулу выше, получаем вероятность

Источник

Показательное распределение

Вы будете перенаправлены на Автор24

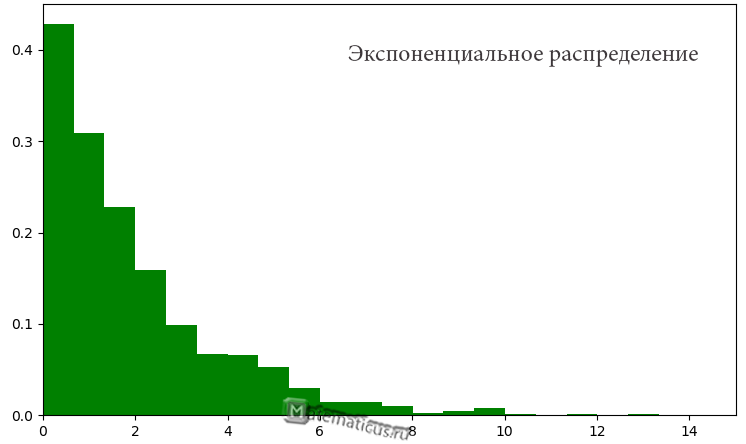
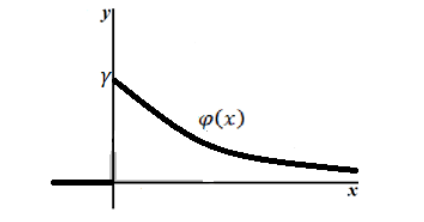
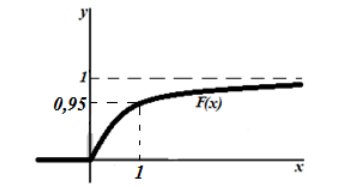
График плотности показательного распределения имеет вид (рис. 1):

Рисунок 2. График плотности показательного распределения.

Функция показательного распределения

Как нетрудно проверить, функция показательного распределения имеет вид:

График функции показательного распределения имеет вид:

Рисунок 4. График функции показательного распределения.

Вероятность попадания случайной величины при показательном распределении

Пример задачи на показательное распределение

Найти плотность распределения и построить её график.

Найти функцию распределения и построить её график.

Найти математическое ожидание, дисперсию и среднее квадратическое отклонение данного распределения.

Источник

2.Показательный (экспоненциальный закон распределения).

Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:

Функция распределения имеет вид:

Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:

То есть при

Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону.

Определить вероятность того, что на ремонт телевизора потребуется не менее 20 дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.

По условию математическое ожидание M(х)=1/λ = 15, откуда параметр λ = 1/15. Тогда плотность вероятности и функция распределения примут вид:

Искомую вероятность P(Х ≥20) можно было найти по формуле, интегрируя плотность вероятности, то есть

но проще это сделать, используя функцию распределения:

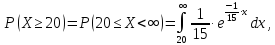
Найдем среднее квадратическое отклонение: σ(X) = М(Х) = 15 дней.

3.Равномерный закон распределения.

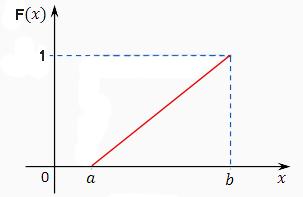
Непрерывная случайная величина Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, то есть

Следовательно, математическое ожидание случайной величины, равномерно распределенной на отрезке (a, b), равняется середине этого отрезка.

Дисперсия имеет вид:

Найдем вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал , принадлежащий целиком отрезку [a, b]:

Функция распределения примет вид:

Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты.

Найти математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания поезда.

Случайная величина X – время ожидания поезда на временном (в минутах) отрезке [0;2] имеет равномерный закон распределения f (x)=1/2.

Поэтому вероятность того, что пассажиру придется ждать не более полминуты, равна 1/4 от равной единице площади прямоугольника, т.е.

Найдем математическое ожидание, дисперсию и среднее квадратическое отклонение:

12. Вероятность заданного отклонения. Правило трех сигм.

Теорема. Вероятность модуля отклонения непрерывной случайной величины X от её математического ожидания на величину сколь угодно малого числа ε>0 находится по формуле:

(*)

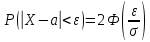
Пусть .

Подставим значение ε в формулу (*), получим:

Итак, с вероятностью сколь угодно близкой к единице можно утверждать, что модуль отклонения нормально распределенной случайной величины от её математического ожидания не превосходит утроенного среднего квадратического отклонения.

Центральная предельная теорема.

Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова.

Если случайная величина Х представляет собой сумму большого числа взаимно ‒ независимых случайных величин, то есть, влияние каждой из которых на всю сумму ничтожно мало, то случайная величинаХ имеет распределение, неограниченно приближающееся к нормальному распределению.

Начальные и центральные моменты непрерывной случайной величины, асимметрия и эксцесс. Мода и медиана.

В прикладных задачах, например в математической ста­тистике, при теоретическом изучении эмпирических распре­делений, отличающихся от нормального распределения, воз­никает необходимость количественных оценок этих различий. Для этой цели введены специальные безразмерные характеристики.

Определение. Мода непрерывной случайной величины ( Мо (X)) – это её наиболее вероятное значение, для которого вероятность p_i или плотность вероятности f(x) достигает максимума.

Определение. Медиана непрерывной случайной величины X (Me(X)) – это такое её значение, для которого выполняется равенство:

P (X Me (X)) =

Геометрически вертикальная прямая x = Me (X) делит площадь фигуры под кривой на две равные части.

В точке X = Me (X), функция распределения F (Me (X)) =

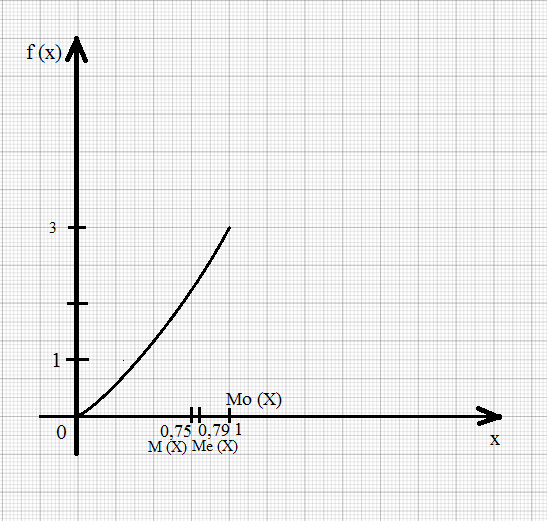
Плотность вероятности f (x) максимальна при x = 1, т.е. f (1) = 3, следовательно, Mo (X) = 1 на интервале [ 0; 1 ].

Для нахождения медианы обозначим Me (X) = b.

Так как Me (X) удовлетворяет условию P (X 3 = .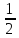

b 3 = 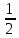; b = » 0,79

M (X) = =+=

== = = 0,75

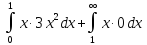
Отметим получившиеся 3 значения Mo (x), Me (X), M (X) на оси Ox:

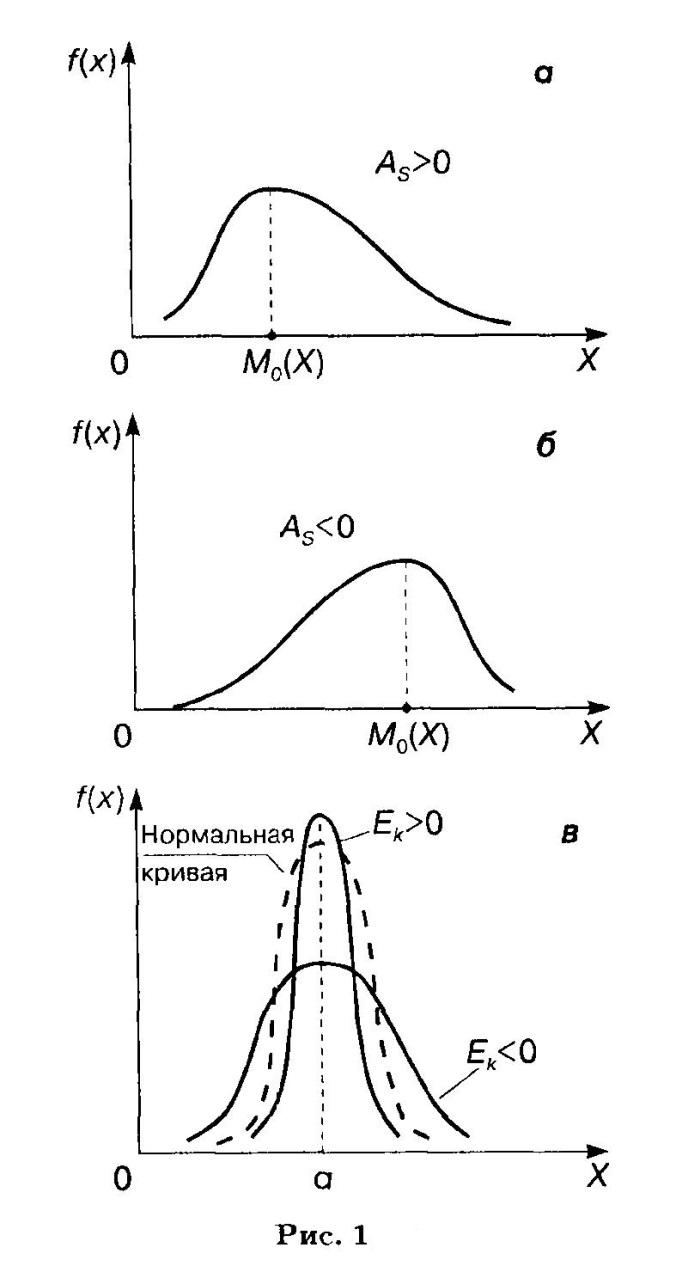
Определение. Асимметрией теоретического распределения называется отношение центрального момента третьего поряд­ка к кубу среднего квадратического отклонения:

Определение. Эксцессом теоретического распределения на­зывается величина, определяемая равенством:

где 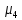‒ центральный момент четвертого порядка.

Для нормального распределения 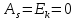. При отклоне­нии от нормального распределения асимметрия положительна, если «длинная» и более пологая часть кривой распределения расположена справа от точки на оси абсцисс, соответствую­щей моде; если эта часть кривой расположена слева от моды, то асимметрия отрицательна (рис. 1, а, б).

Эксцесс характеризует «крутизну» подъема кривой распре­деления по сравнению с нормальной кривой: если эксцесс поло­жителен, то кривая имеет более высокую и острую вершину; в случае отрицательного эксцесса сравниваемая кривая имеет более низкую и пологую вершину.

Следует иметь в виду, что при использовании указанных характеристик сравнения опорными являются предположения об одинаковых величинах математического ожидания и дис­персии для нормального и теоретического распределений.

Пример. Пусть дискретная случайная величина Х задана законом распределения:

Найти: асимметрию и эксцесс теоретического распределения.

Найдем сначала математическое ожидание слу­чайной величины:

Затем вычисляем начальные и центральные моменты 2, 3 и 4-го порядков и среднее квадратическое отклонение:

Теперь по формулам находим искомые вели­чины:

В данном случае «длинная» часть кривой распределения рас­положена справа от моды, причем сама кривая является не­сколько более островершинной, чем нормальная кривая с теми же величинами математического ожидания и дисперсии.

Теорема. Для произвольной случайной величины Х и любого числа

Ԑ>0 справедливы неравенства:

‒ вероятность противоположного неравенства.

Средний расход воды на животноводческой ферме составляет 1000 л в день, а среднее квадратичное отклонение этой случайной величины не превышает 200 л. Оценить вероятность того, что расход воды на ферме в любой выбранный день не превзойдет 2000 л, используя неравенство Чебышева.

Пусть X –расход воды на животноводческой ферме (л).

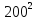
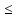
Дисперсия D(X) = . Так как границы интервала 0X 2000 симметричны относительно математического ожиданияМ(Х) = 1000, то для оценки вероятности искомого события можно применить неравенство Чебышева:

То есть не менее, чем 0,96.

Для биномиального распределения неравенство Чебышева примет вид:

Источник