смещенная оценка искомого параметра обладает следующим свойством
Статистические оценки параметров распределения
Вы будете перенаправлены на Автор24
Распределения в математической статистике характеризуется многими статистическими параметрами. Оценка неизвестных параметров распределения на основе различных данных выборки позволяет построить распределения случайной величины.
Статистические оценки можно разделить на несмещенные, смещенные, эффективные и состоятельные.
Готовые работы на аналогичную тему
Генеральная и выборочная средние
Величины генерального и выборочного среднего можно найти по следующим формулам:
С этим понятием связано такое понятие как отклонение от средней. Данная величина находится по следующей формуле:
Среднее отклонение обладает следующими свойствами:
Среднее значение отклонения равно нулю.
Генеральная, выборочная и исправленная дисперсии
Еще одними из основных параметров является понятие генеральной и выборочной дисперсии:
Генеральная дисперсия:
Выборочная дисперсия:
С этими понятия связаны также генеральная и выборочная средние квадратические отклонения:
В качестве оценки генеральной дисперсии вводится понятие исправленной дисперсии:
Также вводится понятие исправленного стандартного отклонения:
Пример решения задачи
Генеральная совокупность задана следующей таблицей распределения:
Найдем для нее генеральное среднее, генеральную дисперсию, генеральное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.
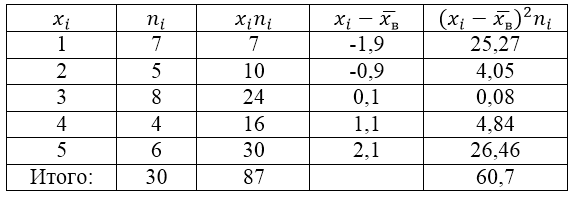
Для решения этой задачи для начала сделаем расчетную таблицу:
Найдем генеральную дисперсию по формуле:
Генеральное среднее квадратическое отклонение:
Исправленное среднее квадратическое отклонение: