соотношение параметров политропного процесса
Зависимость между параметрами газа в политропном процессе
Зависимость между параметрами газа в политропном процессе
Два полубесконечных тела с различными тепловыми свойствами, находящиеся первоначально при различных, но постоянных температурах, внезапно приводят в тесный контакт друг с другом. Людмила Фирмаль
Разделив уравнение на (cf-c») ro, получим его в следующем виде: (5.7). Чтобы ввести обозначение Мы получаем н ^₊^₌0. Интегрируя и усиливая это уравнение от начала до конца процесса、 РТС » = SOP51.(5.10).
Дайте рекомендации относительно глубины закладки трубы, принимая во внимание почвенные условия и влагосодержание грунта. Людмила Фирмаль
Аналогично, если исключить определенный объем, можно увидеть зависимость между давлением и температурой Отсюда (5.12). Поэтому зависимость, представляющая собой изменение параметров газа в политропном процессе, определяется величиной N, которую мы вводим. Это значение называется индикатором политропа и является постоянным для каждого процесса. Мы также рассмотрим процесс в предположении, что теплоемкость постоянна.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Соотношения между параметрами состояния в политропном процессе
Найдем соотношения между параметрами состояния в политропном процессе.
Установим вначале взаимосвязь между давлением и объемом. Используя уравнение (2.22), получим

Из уравнения (2.23) следует, что при n > 0 изменение давления в политропном процессе обратно пропорционально изменению объема. При n 1 изменение объема обратно пропорционально изменению абсолютной температуры. При n 1 и n n > 0 – обратно пропорционально.
Определение изменения внутренней энергии
Изменение внутренней энергии, как и любого другого параметра состояния, не зависит от характера процесса. В случае идеального газа оно всегда определяется с помощью следующих уравнений.
Для элементарного процесса

Для1 кг массы термодинамической системы

Для всей массы термодинамической системы

Определение изменения энтальпии
Для элементарного процесса

Для1 кг массы термодинамической системы

Для всей массы термодинамической системы

Определение изменения энтропии
Изменение энтропии в элементарном термодинамическом процессе по определению выражается соотношением

Используя соотношение первого закона термодинамики (2.13), получим

Если решить уравнение состояния идеального газа, то получим 

Интегрируя соотношение (2.33), получим изменение энтропии в конечном процессе для 1 кг термодинамической системы

Используя выражение первого закона термодинамики в форме (2.16), и проделав аналогичные преобразования, получим

Определение теплоты, подводимой (отводимой)
В ходе политропного процесса
Количество тепла, подводимого (отводимого) в ходе политропного процесса, можно определить с помощью уравнения первого закона термодинамики

Сказанное не исключает возможности определения dq с помощью теплоемкости

Используя соотношение (2.19) найдем теплоемкость политропного процесса

где 


Соотношение параметров политропного процесса
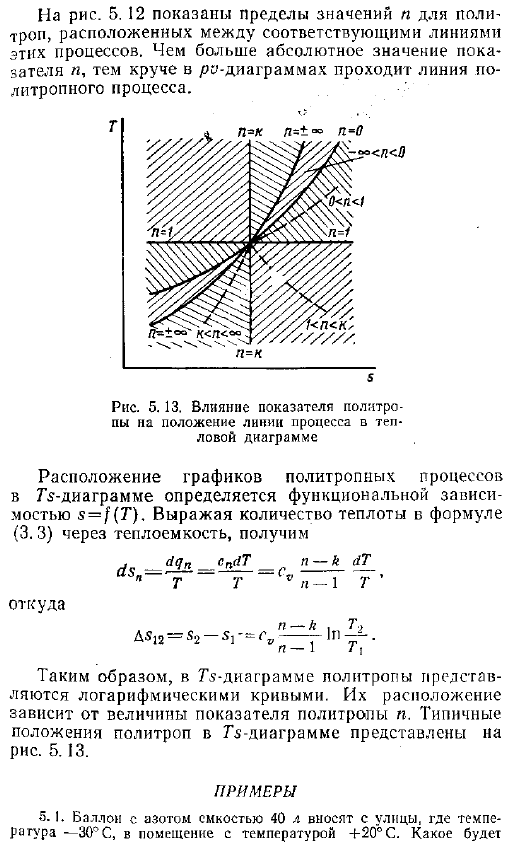
В переводе на русский язык слово политропа означает многообразие, применительно к процессам это многообразие закономерностей. Закономерность энергетических взаимодействий приведет к закономерному изменению членов первого закона термодинамики для данного тела. В случае обратимого (без трения) процесса соблюдается первый закон термодинамики δq=du+δl. Для закономерного процесса имеется определенное соотношение между членами уравнения первого закона термодинамики. Обычно за величину, определяющую закономерность энергетического взаимодействия, принимают отношение изменения внутренней энергии к количеству подведенной теплоты
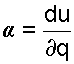 |
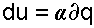 |
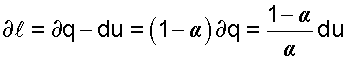 |
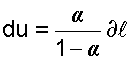 |
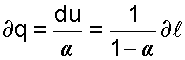 |
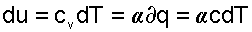 |
Поскольку α=const, то и теплоемкость политропного процесса для идеального газа будет величиной постоянно
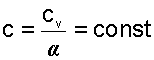 |
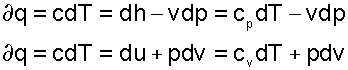 |
Преобразуем эти уравнения, переместив члены с теплоемкостями в левую часть
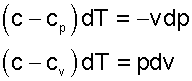 |
После деления правых и левых частей равенств друг на друга получим постоянную величину
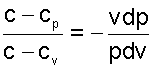 |
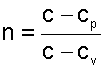 |
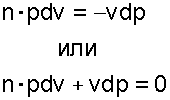 |
Разделив последнее равенство на произведение pv, получим
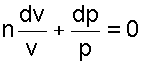 |
После интегрирования последнего равенства получаем
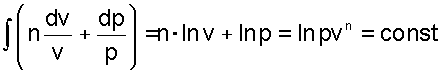 |
или окончательно:
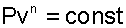 |
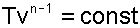 |
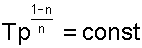 |
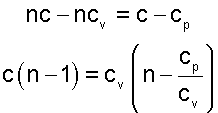 |
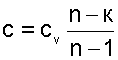 |
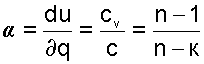 |
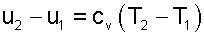 |
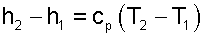 |
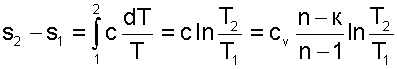 |
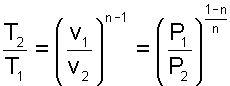 |
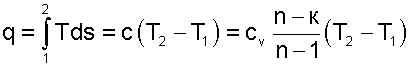 |
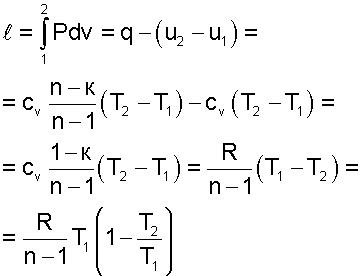 |









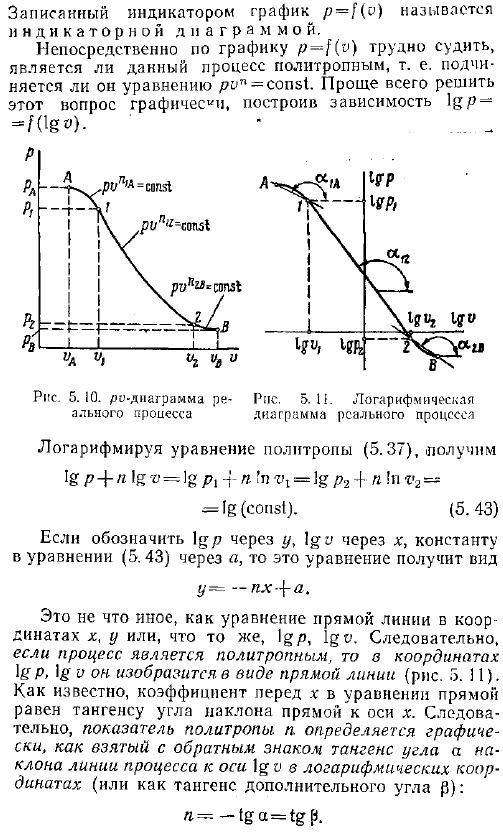



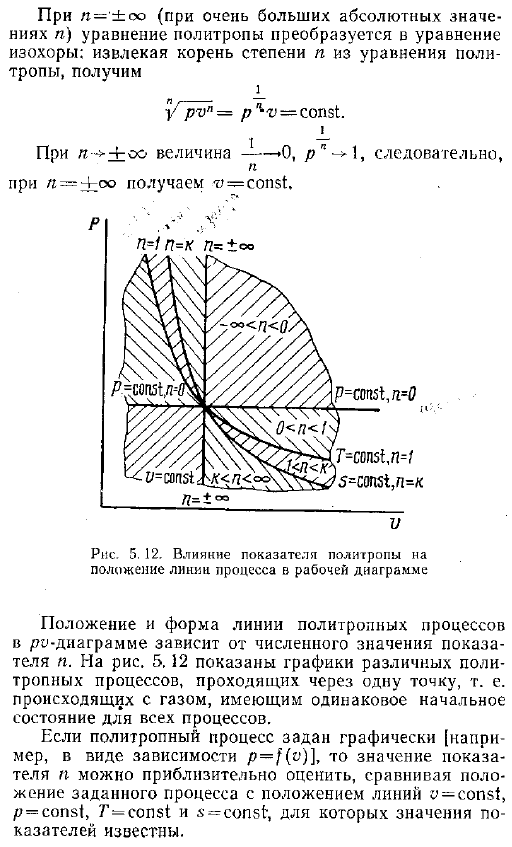



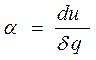 (4-1)
(4-1)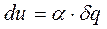
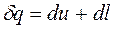 , отсюда
, отсюда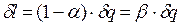
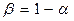 — величина b показывает какая часть подводимого тепла идёт на совершение работы.
— величина b показывает какая часть подводимого тепла идёт на совершение работы.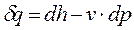 и
и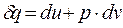
 ;
; 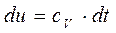 ;
;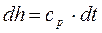 , тогда можно записать
, тогда можно записать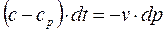 и
и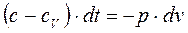 , деля (а) на (б) получим
, деля (а) на (б) получим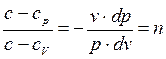 (4-2)
(4-2)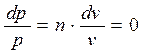 (4-3)
(4-3)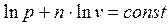 , или
, или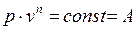 (4-4)
(4-4)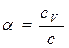 , откуда
, откуда 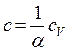 (4-5)
(4-5)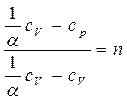 , числитель и знаменатель разделим на cv , получим:
, числитель и знаменатель разделим на cv , получим: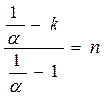 , приводим к общему знаменателю, получим
, приводим к общему знаменателю, получим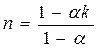 (4-6)
(4-6)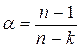 (4-7)
(4-7)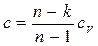 — теплоёмкость политропного процесса.
— теплоёмкость политропного процесса.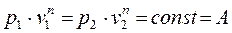 , найдём
, найдём (в)
(в)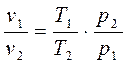 (г)
(г)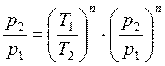 , или
, или 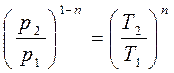 откуда
откуда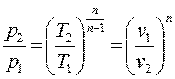 , или используя (в), получим
, или используя (в), получим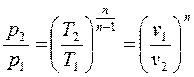 (4-9)
(4-9)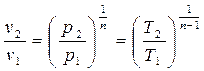 (4-10),
(4-10),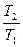 , получим:
, получим: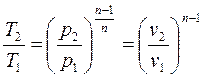 (4-11)
(4-11)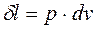 , из уравнения (4-4) политропы
, из уравнения (4-4) политропы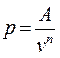 , откуда
, откуда 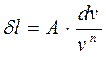
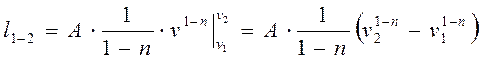 (д)
(д) (4-12)
(4-12)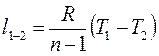 (4-13)
(4-13)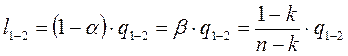 (4-14)
(4-14)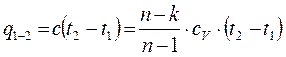 (4-15)
(4-15)