состояние макроскопических тел определяется макроскопическими параметрами к их числу относятся
§ 3.1. Состояние макроскопических тел в термодинамике
В этой главе вы узнаете немало нового о физической величине, которую каждый день упоминают в сводках погоды: о температуре, о том, как она строго научно определяется в физике.
Здесь же вы познакомитесь с эмпирическими законами поведения самого простого макроскопического тела — газа. Именно открытие и исследование газовых законов дало возможность ввести понятие абсолютной температуры.
Вы знаете, как характеризуется состояние системы частиц (или тел) в классической механике. Посмотрим, как определяется состояние макроскопических тел в термодинамике.
В механике состояние системы частиц определяется их положениями (координатами) и скоростями. По начальным координатам и скоростям можно при заданных силах найти положение и скорости частиц в любой последующий момент времени.
Определить подобным образом внутреннее состояние макроскопических тел, состоящих из огромного числа частиц, нельзя. Однако поведение макроскопических тел можно охарактеризовать немногим числом физических величин, относящихся не к отдельным молекулам, слагающим тела, а ко всему макроскопическому телу в целом. К числу таких величин относятся объем V, давление р, температура t и др.
Так, газ данной массы всегда занимает некоторый объем, имеет определенные давление и температуру. Объем и давление представляют собой механические величины, описывающие состояние газа. Понятие температуры в механике не рассматривается, так как она характеризует внутреннее состояние тел.
Макроскопические параметры
Любое макроскопическое тело или группа макроскопических тел называется термодинамической системой (от греч. systema — целое, составленное из частей).
Величины, характеризующие состояние термодинамической системы без учета молекулярного строения тел, называют макроскопическими (или термодинамическими) параметрами. Макроскопические параметры не исчерпываются объемом, давлением и температурой. Например, для смеси газов нужно знать концентрации отдельных компонентов смеси. Если вещество находится в электрическом или магнитном поле, то необходимо задать характеристики этих полей в веществе.
В то же время форма сосуда, в котором находится газ, не является существенной для определения его состояния. Например, кислород в сосуде, изображенном на рисунке 3.1, а, будет находиться точно в таком же состоянии, в каком и кислород в сосуде другой формы (рис. 3.1, б), если объемы сосудов, массы и температуры газов одинаковы. В частности, давления газов в обоих сосудах равны. Не зависит от формы сосуда сжимаемость газа и его другие свойства.
Давление газа в молекулярно-кинетической теории
На примере давления газа выясним, какой смысл имеют макроскопические параметры с молекулярно-кинетической точки зрения.
Пусть газ находится в закрытом сосуде. Манометр показывает давление газа р0. Как возникает это давление? Каждая молекула газа, ударяясь о стенку, в течение малого промежутка времени действует на нее с определенной силой. В результате беспорядочных ударов о стенку сила, действующая со стороны всех молекул на поверхность стенки единичной площади, т. е. давление, будет быстро меняться со временем примерно так, как показано на рисунке 3.2. Однако действия, вызванные ударами отдельных молекул, настолько слабы, что манометром они не регистрируются. Манометр фиксирует среднюю по времени силу, действующую на каждую единицу площади поверхности его чувствительного элемента — мембраны. Несмотря на небольшие изменения давления, среднее значение давления р0 практически оказывается вполне определенным, так как ударов о стенку очень много, а массы молекул очень малы.
§ 19. Макроскопическая система и характеристики её состояния
Макроскопическая система
1. Любое тело — твёрдое, жидкое, газообразное — состоит из огромного числа частиц, которые находятся в непрерывном, хаотическом движении и взаимодействуют между собой.
Тела, состоящие из очень большого числа частиц: атомов, молекул, ионов, называют макроскопическими телами или макроскопическими системами. Примерами макроскопических систем могут служить газ в баллоне, жидкость в сосуде, твёрдое тело.
Раздел физики, в котором изучают физические свойства макроскопических тел (макроскопических систем) в различных агрегатных состояниях на основе рассмотрения их внутреннего (молекулярного) строения, называют молекулярной физикой.
Состояние макроскопической системы
2. Напомним, что в механике объектом, изменение состояния которого исследуется, является механическая система (материальная точка или весьма небольшое их число). Состояние механической системы характеризуется параметрами состояния, к которым относятся координата и импульс. При изменении состояния системы параметры изменяются. Их значение в любой момент времени можно однозначно определить, если известны параметры начального состояния системы и закон их изменения (кинематические уравнения движения, законы Ньютона).
Тепловые явления также связаны с изменением состояния макроскопических тел. Например, если поставить на включённую плиту сосуд с водой, то состояние системы «сосуд—вода» начнёт изменяться: через некоторое время сосуд и вода нагреются, их объёмы увеличатся. Если быстро сжать газ в цилиндре, то его состояние тоже изменится: объём газа уменьшится и он нагреется.
Из рассмотренных примеров видно, что состояние макроскопической системы так же, как и механической, характеризуется определёнными параметрами. Такими параметрами являются объём, давление, температура. Они характеризуют состояние макроскопической системы как целого, поэтому их называют макроскопическими параметрами состояния системы.
Вместе с тем вам известно, что температура макроскопической системы связана со скоростью движения её молекул: чем больше скорость движения молекул, тем выше температура. Со скоростью движения молекул связано и давление газа на стенки сосуда; оно также зависит от массы молекул. Таким образом, значения макроскопических параметров связаны с характеристиками частиц, составляющих макроскопическую систему.
Тест с ответами: “Газовые законы”
1. Состояние макроскопических тел определяется макроскопическими параметрами. К их числу относится:
а) давление +
б) молярная масса
в) универсальная газовая постоянная
2. Запишите уравнение Менделеева-Клапейрона:
а) Vp=(m/M)RT
б) pV=(m/M)RT +
в) pV=(m/M)-RT
3. Состояние макроскопических тел определяется макроскопическими параметрами. К их числу относится:
а) газовая постоянная
б) масса газа
в) объем +
4. Какие физические параметры одинаковы у двух любых физических тел, находящихся между собой в тепловом равновесии:
а) температура +
б) давление
в) средняя квадратичная скорость
5. Состояние макроскопических тел определяется макроскопическими параметрами. К их числу относится:
а) молярная масса
б) масса газа
в) температура +
6. Вычислите давление водорода массой 0,02кг в сосуде объемом 8,3 м³ при температуре 100 ºС:
а) 100 Па
б) 1000 Па +
в) 373 Па
7. Чтобы давление газа увеличилось в 3 раза при постоянном объеме, его температуру надо:
а) уменьшить в 4 раза
б) уменьшить в 3раза
в) увеличить в 3 раза +
9. Выражение для вычисления плотности газа:
а) pV/T
б) pV/RT
в) Mp/RT +
10. В сосуде находится газообразный водород, количество вещества которого 1 моль. Сколько (примерно) молекул водорода находится в
сосуде:
а) 12•10²³
б) 6•10²³ +
в) 2•10²³
11. Определите начальную температуру, если при постоянном давлении идеальный газ нагрели на 1 °С, при этом его объём увеличился на 0,35 % от первоначального значения:
а) 286 К +
б) 386 К
в) 288 К
12. Вычислите давление кислорода массой 0,032 кг в сосуде объемом 8,3 м³ при температуре 100 ºС:
а) 100 Па
б) 373 Па +
в) 830 Па
13. При изотермическом процессе после сжатия газа его объём уменьшился в 1,4 раза, а давление изменилось на 100 кПа. Определите конечное давление:
а) 350 кПа +
б) 530 кПа
в) 250 кПа
14. Какое (примерно) значение температуры выраженной в Кельвинах, соответствует температуре 20ºС:
а) 253 К
б) 273 К
в) 293 К +
15. Баллон ёмкостью 20 л заполнен воздухом под давлением 0,4 МПа. Баллон соединяют тонкой трубкой с другим баллоном, из которого воздух откачан. Определите объём второго баллона, если конечное давление составило 10 в пятой степени Па. Процесс протекает при постоянной температуре:
а) 60 л +
б) 80 л
в) 40 л
16. В сосуде находится Нe, количество вещества которого 2 моль. Сколько (примерно) атомов гелия в сосуде:
а) 2•10²³
б) 12•10²³ +
в) 12•10²6
17. При изохорном процессе давление идеального газа увеличилось на 100 кПа. На сколько при этом увеличилась температура, если начальное давление составляло 50 кПа, а начальная температура — 27 °С:
а) 800 °С
б) 400 °С
в) 600 °С +
18. Изобарным процессом термодинамической системы называют процесс перехода системы из одного состояния в другое при какой-то одной постоянной величине:
а) T=const
б) P=const +
в) V=const
19. В сосуде переменного объёма при постоянной температуре давление газа увеличили на 100 к Па, при этом объём изменился в 1,1 раза. Определите первоначальное давление:
а) 10 МПа
б) 11 МПа
в) 1 МПа +
20. Как изменится давление идеального одноатомного газа при увеличении его объёма в 3 раза и уменьшении температуры в 2 раза:
а) останется прежним
б) уменьшится в 6 раз +
в) увеличится в 6 раз
21. В сосуде переменного объёма при постоянном давлении газ занимает объём 500 л при температуре 27 °С. Какой объём будет занимать газ при температуре −123 °С:
а) 250 дм³ +
б) 550 дм³
в) 150 дм³
22. В баллоне при неизменной массе газа температура увеличилась от 10 °С до 50 °С. Как изменилось давление газа:
а) уменьшилось в 5 раз
б) увеличилось в 1,14 раза +
в) увеличилось в 5 раз
23. В баллоне постоянного объёма находится идеальный газ при температуре 17 °С и давлении 1 МПа. Температуру газа понизили до −23 °С. Определите изменение давления газа:
а) 2,4 • 105 Па
б) 1,4 • 115 Па
в) 1,4 • 105 Па +
24. Как изменится давление идеального газа при увеличении абсолютной температуры и объема в 2 раза:
а) уменьшится в 4 раза
б) не изменится +
в) увеличится в 4 раза
25. При постоянной температуре объём газа в некотором сосуде уменьшили от 12 до 8 л, при этом изменение давления составило 200 кПа. Определите начальное давление газа:
а) 70 кПа
б) 30 кПа
в) 50 кПа +
26. Оцените массу воздуха в помещении объемом 200 м³:
а) ≈ 20 кг
б) ≈ 200 кг +
в) ≈ 2000 кг
27. В цилиндре постоянного объёма газ переводят из состояния с атмосферным давлением и температурой 600 К в состояние с давлением 152 кПа. Определите изменение температуры газа:
а) ≈ 300 К +
б) ≈ 500 К
в) ≈ 100 К
28. В сосуде объемом 83 дм³ находится 20 г водорода при температуре 127°С. Определите его давление:
а) 800 Па
б) 8 • 10 в пятой степени Па
в) 4 • 10 в пятой степени Па +
30. При изохорном процессе в газе не изменяется (при m = const) его:
а) температура
б) объем +
в) давление
§ 59. Температура и тепловое равновесие
Что измеряют термометры?
Что означают слова: «Я измерил температуру тела»?
Что именно характеризует температура?
Макроскопические параметры
Состояние макроскопических тел, в частности газов, и процессы изменения их состояний можно охарактеризовать немногим числом физических величин, относящихся не к отдельным молекулам, из которых состоят тела, а ко всем молекулам в целом. К числу таких величин относятся объём V, давление р, температура t.
Так, газ данной массы, находящийся в сосуде, всегда занимает объём этого сосуда и имеет определённые давление и температуру. Объём и давление представляют собой механические величины, которые помогают описывать состояние газа. Температура в механике не рассматривается, так как она характеризует внутреннее состояние тела.
Запомни
Величины, характеризующие состояние макроскопических тел без учёта их молекулярного строения (V, р, t), называют макроскопическими параметрами.
Однако макроскопические параметры не исчерпываются объёмом, давлением и температурой.
Например, для описания состояния смеси газов нужно ещё знать концентрации отдельных компонентов или их массы. Обычный атмосферный воздух представляет собой смесь газов.
Холодные и горячие тела
Центральное место во всём учении о тепловых явлениях занимает понятие температура. Все мы хорошо знаем различие между холодными и горячими телами. На ощупь мы определяем, какое тело нагрето сильнее, и говорим, что это тело имеет более высокую температуру. Таким образом,
Важно
температура характеризует степень нагретости тела (холодное, тёплое, горячее).
Для её измерения был создан прибор, называемый термометром. Его устройство основано на свойстве тел изменять объём при нагревании или охлаждении.
Термодинамический метод описания равновесных систем. Макросостояние. Макроскопические параметры. Уравнение состояния.
Термодинамический метод изучает свойства тел, не вдаваясь в их микроскопическую структуру, а опираясь на фундаментальные законы ( начала термодинамики), установленные обобщением экспериментальных фактов. Состояние термодинамической системы будет равновесным, если все параметры cостояния имеют определенные значения, не изменяющиеся с течением времени.
Макроскопическое Состояние (Макросостояние) Системы
Макроскопическое Состояние (Макросостояние) Системы определяется значениями ее термодинамических параметров: давления p, температуры Т, удельного объема v, внутренней энергии U и т. п. Для определения макроскопического состояния однокомпонентной системы достаточно знать значения любых 2 независимых параметров (напр., Т и p или Т и v).
Макроскопические параметры: масса системы, объем системы, температура системы, количества вещества в системе, давление системы на внешние тела, внутренняя энергия системы.
Уравнение состояния — уравнение, связывающее между собой термодинамические (макроскопические) параметры системы, такие, как температура, давление, объём, химический потенциал и др. Уравнение состояния можно написать всегда, когда можно применять термодинамическое описание явлений. При этом реальные уравнения состояний реальных веществ могут быть крайне сложными.
Состояние термодинамического равновесия системы частиц. Тепловое движение.
Согласно опыту любая замкнутая система, состоящая из большого числа взаимодействующих частиц, с течением времени самопроизвольно переходит в особое конечное состояние, которое называется термодинамическим равновесием. Состояние термодинамического равновесия является устойчивым относительно малых возмущений как начальных условий, так и самого конечного состояния. Вывод о существовании равновесного состояния термодинамической системы иногда называют нулевым началом термодинамики. Следует отметить, что переход системы в состояние термодинамического равновесия не может быть описан только на основе законов механического движения отдельной частицы. Иными словами, временная динамика такой системы частиц в целом имеет качественные отличия от динамики отдельной частицы.
В состоянии термодинамического равновесия частицы совершают особое движение, которое называется тепловым. Тепловое движение сложных составных частиц может быть поступательным, вращательным и колебательным. Интенсивность любого теплового движения характеризуется с помощью макроскопической величины, называемой температурой. В состоянии термодинамического равновесия температура T одинакова для всех макроскопических частей системы (условие теплового равновесия), что обеспечивает отсутствие теплообмена между макроскопическими частями системы. В Международной системе единиц СИ температура измеряется в кельвинах (K).
Модель идеального газа. Температура. Давление. Уравнение Клапейрона-Менделеева.
Модель идеального газа
Абстрактная модель, отражающая существенные черты явления, аналогичная материальной точке.
1. Молекулы (или атомы) газа не имеют собственного объема, то есть рассматриваются как материальные точки.
2. Силы взаимодействия между атомами и молекулами идеального газа пренебрежимо малы. Поэтому потенциальной энергией взаимодействия можно пренебречь. Отсюда, внутренняя энергия идеального газа – сумма кинетических энергий хаотического движения всех молекул. Взаимодействие же молекул сводится к упругим столкновениям.
Справедливо для газов в разреженном состоянии. Отсюда – идеальный газ: система невзаимодействующих материальных точек.
Температура
Если два тела находятся в состоянии термодинамического равновесия, то есть не обмениваются энергией путем теплопередачи, то этим телам приписывается одинаковая температура. Температура– физическая величина, характеризующая степень нагретости тел и определяет направление передачи тепла. Если между телами происходит направленный теплообмен, то телу отдающему энергию приписывают большую температурупо сравнению с телом, получающим тепловую энергию.
В физике и технике за абсолютную шкалу температур принята шкала Кельвина, названная в честь знаменитого английского физика, лорда Кельвина.
— шкала Фаренгейта (немецкий физик 1724г) – точка таяния льда 32°F, точка кипения воды 212°F.
— шкала Цельсия (шведский физик 1742г) – точка таянья льда 0°С, точка кипения воды 100°С. 0°С = 273,15 К.
Давление
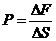
где ΔF–сила, действующая на поверхность площадь ΔS.
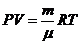
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.




