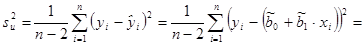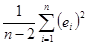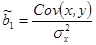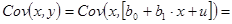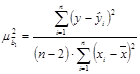состоятельность оценок параметров регрессии означает что
10. Выбор вида регрессионной модели и оценка ее параметров
На данном этапе устанавливается однофакторная или многофакторная будет строиться модель и вид модели (линейный или нелинейный).
Обоснование вида модели состоит в выборе вида функции (некоторого аналитического выражения), с помощью которого можно будет описать изменение исследуемого показателя под воздействием факторов.
К обоснованию вида функции идут двумя путями: Теоретическим (анализируя экономическую природу 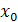

Наиболее употребительными выражениями при описании связи одного фактора и исследуемого показателя являются:
В качестве нелинейных моделей применяются
Для оценки значений параметров регрессионной модели чаще всего используется Метод наименьших квадратов (МНК).Этот метод можно применить как для линейных моделей, так и для нелинейных, допускающих преобразование их к линейному виду путем замены переменных или дифференцированием.
При использовании МНК делаются определенные предпосылки относительно случайной составляющей ε. В модели 

Остатки представляют собой независимые случайные величины, и их среднее значение равно 0; они имеют одинаковую (постоянную) дисперсию и подчиняются нормальному распределению.
Статистические проверки параметров регрессии, показателей корреляции основаны на непроверяемых предпосылках распределения случайной составляющей 
Коэффициенты регрессии, найденные из системы нормальных уравнений, представляют собой выборочные оценки характеристики силы связи. Их несмещенность является желательным свойством, т. к. только в этом случае они могут иметь практическую значимость.
Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Оценки считаются Эффективными, если они характеризуются наименьшей дисперсией. Поэтому несмещенность оценки должна дополняться минимальной дисперсией. Состоятельность оценок характеризует увеличение их точности с увеличением объема выработки.
Указанные критерии оценок (несмещенность, состоятельность, эффективность) обязательно учитываются при разных способах оценивания. Метод наименьших квадратов строит оценки регрессии на основе минимизации суммы квадратов остатков (
Исследование остатков 
С цель проверки случайного характера остатков 






Вторая предпосылка МНК относительно нулевой средней величины остатков означает, что 





Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t и F. Вместе с тем оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т. е. при нарушении пятой предпосылки метода наименьших квадратов.
Наличие гетероскедастичности будет сказываться на уменьшении эффективности оценок 
Наличие гетероскедастичности в остатках регрессии можно проверить с помощью ранговой корреляции Спирмэна. Суть проверки заключается в том, что в случае гетероскедастичности абсолютные остатки 


Где ρ – абсолютная разность между рангами значений 

Статистическую значимость ρ можно определить с помощью t-критерия:

Принято считать, что если 


При построении регрессионных моделей чрезвычайно важно соблюдение четвертой предпосылки МНК – отсутствие автокорреляции остатков, т. е. распределения остатков 



Отсутствие автокорреляции остатков обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.
До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Для того, чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т. е. качественные переменные необходимо преобразовать в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными.
Качественные признаки могут приводить к неоднородности исследуемой совокупности, что может быть учтено при моделировании двумя путями:
Качественный фактор может иметь только два состояния, которым будут соответствовать 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели.
Коэффициент регрессии при фиктивной переменной интерпретируется как среднее изменение зависимой переменной при переходе от одной категории к другой при неизменных значениях остальных параметров. На основе t-критерия Стьюдента делается вывод о значимости влияния фиктивной переменной, существенности расхождения между категориями.
Оценка регрессии



1.3.1. Оценка дисперсии случайной составляющей – 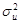
Оценка дисперсии случайной составляющей в случае ной линейной регрессии.
Несмещенной оценкой дисперсии случайной составляющей является:
где ei – остаток, равный разности между фактическим и рассчитанным по уравнению регрессии значениями у:
Оценкой ковариационной матрицы случайных составляющих Сu будет матрица: 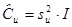
При повторении выборок того же самого объема n из той же самой генеральной совокупности и при тех же самых значениях объясняющих переменных х наблюдаемые значения зависимой переменной у будут случайным образом варьироваться (за счет случайного характера случайной составляющей u). Следовательно, будут варьироваться и зависеть от у1. уn значения оценок параметров регрессии (j = 0; 1] и оценка дисперсии случайной составляющей.
Покажем на примере 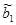
МНК-оценка коэффициента регрессии, как было показано в п. 1.2.3, рассчитывается как отношение ковариации x и y к дисперсии х:
Так как y зависит от случайной составляющей u (y=b0+b1x+u), то ковариация 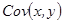
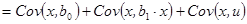
Причем из свойств ковариации (см п. 1.2.2) следует, что:
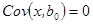
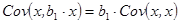
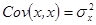
Тогда 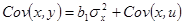
В результате МНК-оценка может быть разложена на случайную и неслучайную составляющие:
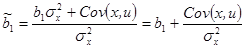
т.е. МНК-оценка 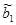
1) постоянной величины, равной истинному значению коэффициента b1;
2) случайной составляющей Cov(х, u), которая обусловливает отклонения оценки коэффициента регрессии от истинного значения.
Аналогично можно показать, что МНК-оценка 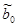
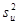
Следует заметить, что на практике мы не можем разложить оценки параметров регрессии и 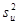
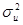
Однако приведенное выше разложение оценок позволяет получить некоторую теоретическую информацию об их свойствах.
Свойства МНК-оценок. Критериями лучшего способа оценивания является требование состоятельности, несмещенности и эффективности оценок, найденных данным способом.
Способ оценивания дает состоятельные оценки, если при бесконечно большом объеме выборки значение статистической оценки стремится к искомому значению параметра (характеристики) генеральной совокупности.
Способ оценивания дает несмещенные оценки, если математическое ожидание оценки при данном способе оценивания тождественно искомому параметру (характернее генеральной совокупности (при любом объеме выборки).
Оценка, полученная при данном способе оценивания называется эффективной, если ее дисперсия минимальна (при заданном объеме выборки n).
МНК-оценки параметров и дисперсии случайной составляющей являются «наилучшими» (состоятельными, несмещенными и эффективными) оценками.
Докажем, что 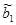
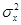
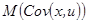
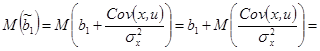
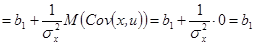
То есть 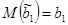
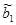
Аналогично доказывается несмещенность оценки 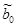
Эффективность МНК-оценок доказывается с помощью теоремы Гаусса-Маркова, которая гласит:
Метод наименьших квадратов дает оценки, имеющие наименьшую дисперсию в классе всех линейных несмещенных оценок, если выполняются предпосылки нормальной линейной регрессионной модели (см. п. 1.2.2).
Ковариационная матрица МНК-оценок параметров регрессии – матрица ковариаций оценок параметров. Для случая парной регрессии это матрица размером 2´2:
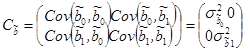
Данная матрица в соответствии с методом наименьших квадратов рассчитывается следующим образом:
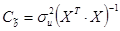
На главной диагонали данной матрицы, находятся дисперсии МНК-оценок параметров. Для случая парной линейной регрессии формулы расчета дисперсий МНК-оценок параметров следующие:
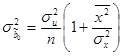
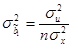
где 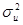
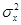
Так как 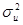
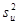
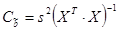
Формулы расчета оценок дисперсий 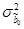
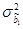
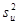
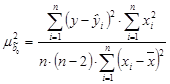
Корень из оценки дисперсии 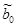
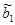
Множественная регрессия и корреляция
Тестовые задания
Парная регрессия и корреляция
1. Наиболее наглядным видом выбора уравнения парной регрессии является:
2. Рассчитывать параметры парной линейной регрессии можно, если у нас есть:
б) не менее 7 наблюдений;
3. Суть метода наименьших квадратов состоит в:
б) минимизации дисперсии результативного признака;
4. Коэффициент линейного парного уравнения регрессии:
а) показывает среднее изменение результата с изменением фактора на одну единицу;
5. На основании наблюдений за 50 семьями построено уравнение регрессии 


6. Суть коэффициента детерминации 
б) характеризует долю дисперсии результативного признака 
7. Качество модели из относительных отклонений по каждому наблюдению оценивает:
а) коэффициент детерминации 
8. Значимость уравнения регрессии в целом оценивает:
а) 
9. Классический метод к оцениванию параметров регрессии основан на:
в) шаговом регрессионном анализе.
10. Остаточная сумма квадратов равна нулю:
11. Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
б) 
12. Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
в) 
13. Общая сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
а) 
14. Для оценки значимости коэффициентов регрессии рассчитывают:
в) коэффициент детерминации 
15. Какое уравнение регрессии нельзя свести к линейному виду:
в) 
16. Какое из уравнений является степенным:
б) 
17. Параметр 
б) коэффициентом эластичности;
18. Коэффициент корреляции 
19. Для функции 
б) 
20. Какое из следующих уравнений нелинейно по оцениваемым параметрам:
в) 
Множественная регрессия и корреляция
1. Добавление в уравнение множественной регрессии новой объясняющей переменной:
б) увеличивает значение коэффициента детерминации;
2. Скорректированный коэффициент детерминации:
в) меньше или равен обычному коэффициенту детерминации;
3. С увеличением числа объясняющих переменных скорректированный коэффициент детерминации:
4. Число степеней свободы для остаточной суммы квадратов в линейной модели множественной регрессии равно:
б) 
5. Число степеней свободы для общей суммы квадратов в линейной модели множественной регрессии равно:
а) 
6. Число степеней свободы для факторной суммы квадратов в линейной модели множественной регрессии равно:
в) 
7. Множественный коэффициент корреляции 



8. Для построения модели линейной множественной регрессии вида 
9. Стандартизованные коэффициенты регрессии 
а) позволяют ранжировать факторы по силе их влияния на результат;
10. Частные коэффициенты корреляции:
в) характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании других факторов, включенных в уравнение регрессии.
11. Частный 
б) служит мерой для оценки включения фактора в модель;
12. Несмещенность оценки параметра регрессии, полученной по МНК, означает:
б) что математическое ожидание остатков равно нулю;
13. Эффективность оценки параметра регрессии, полученной по МНК, означает:
а) что она характеризуется наименьшей дисперсией;
14. Состоятельность оценки параметра регрессии, полученной по МНК, означает:
в) увеличение ее точности с увеличением объема выборки.
15. Укажите истинное утверждение:
в) при наличии гетероскедастичности оценки параметров регрессии становятся смещенными.
16. При наличии гетероскедастичности следует применять:
17. Фиктивные переменные – это:
а) атрибутивные признаки (например, как профессия, пол, образование), которым придали цифровые метки;
18. Если качественный фактор имеет три градации, то необходимое число фиктивных переменных: