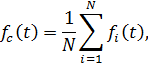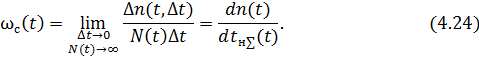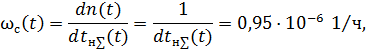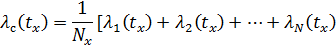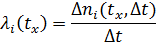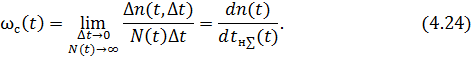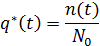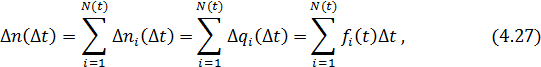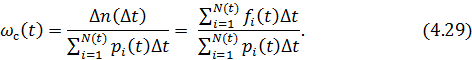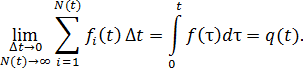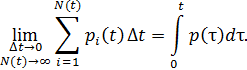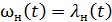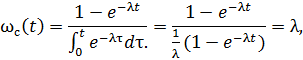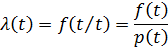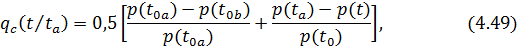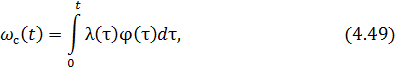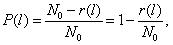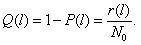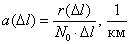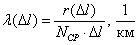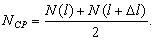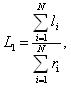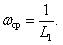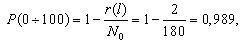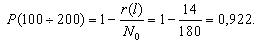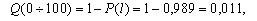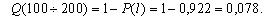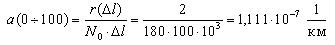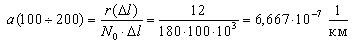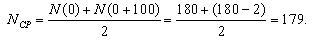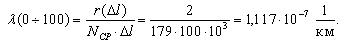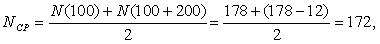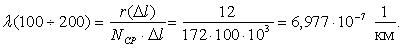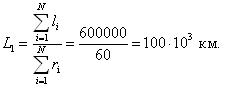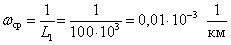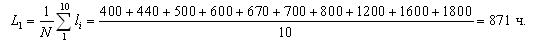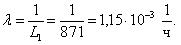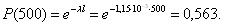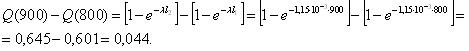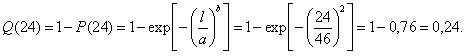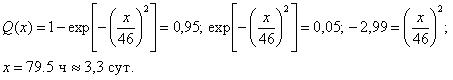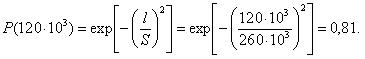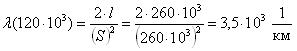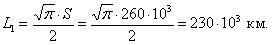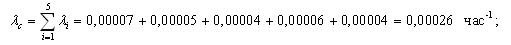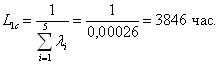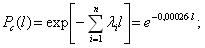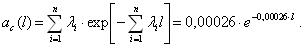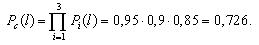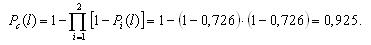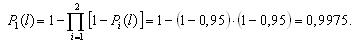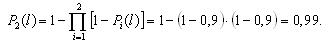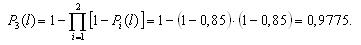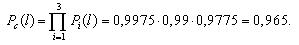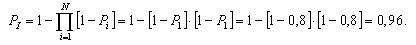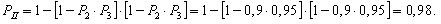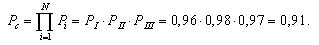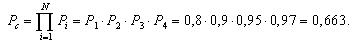среднее значение параметра потока отказов

11.07.202211.07.2022 admin 0 Comments

Параметр потока отказов для системы

функционирования с полным восстановлением

Для схемы функционирования с полным восстановлением изделий в момент отказа существуют различные формы представления параметра потока отказов ω(t).

В практике многолетней эксплуатации авиационной техники наработка отдельных изделий существенно различается. Самолеты и даже авиадвигатели на одном самолете имеют различные наработки. В процессе эксплуатации происходит ремонт и замена объектов авиационного и электрорадиооборудования.

Различие в наработках объясняется разными сроками поступления изделий на эксплуатацию, случайными моментами отказов и замен, регулированием сроков регламентных и плановых ремонтных работ и т.п.

В соответствии с отмеченной схемой функционирования на рис. 4.6 приведены плотности вероятности) однотипных изделий с различной наработкой.

Соответственно начало зависимости плотности вероятности отказа каждого i-го изделия сдвинуто на Δt. относительно соседних изделий.

f(t)

Δt_з

t_x

t_x1

Рис. 4.6. Плотности распределения изделий c распределенной наработкой

В каждый рассматриваемый момент наработки t для совокупности работающих изделий получается среднее значение плотности:

где 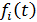— плотность вероятности отказа i-го изделия в момент t.

На основании этого можно сделать предположение, что при достаточно большом удалении наработки t от начала координат значение 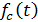стремится к постоянной величине.

Как и в предыдущем случае, определим параметр потока отказов как предел отношения числа отказов на малом интервале наработки Δt → 0 к общей наработке большого числа N(t)→ ∞изделий на этом интервале времени Δt:

Функционирует СНС из 24 спутников. В среднем один раз в 5 лет происходит случайный отказ одного спутника. Найдем параметр потока отказов. Суммарная наработка: 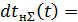24·365·5·24=8760·5·24=1051200 ч, Параметр потока отказов:

В рассматриваемом случае с самого начала (t ≥ 0) параметр потока является средним параметром для всей совокупности одновременно работающих изделий в любой момент t. Поэтому в обозначении этого параметра ставится индекс с: 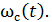Таким образом, средний параметр потока отказов в момент t есть число отказов, приходящееся на единицу времени суммарной наработки большого числа изделий на бесконечно малом интервале наработки (сравните с определением интенсивности отказов: интенсивность отказов есть число отказов в единицу времени, приходящееся на одно исправное изделие в момент времени t).

Рассмотрим физическую связь среднего параметра потока отказовс интенсивностью отказов (рис. 4.7).

λ(t)

1 2 3 4 ….

Δt

t_x

Рис. 4.7. Совмещение интенсивностей отказов изделийс распределенной наработкой

Для момента, например, t _xсреднее значение интенсивности отказов запишется так:

— число изделий, работающих в момент t_x.

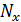
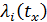
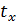
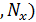
Значения определяются из i-йзависимости в момент .(i=1,2. .

Последнее соотношение можно записать для любого N(t):

Сравнив это соотношение с (4.24), можно увидеть, что 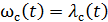, т.е. для рассматриваемой схемы параметр потока отказов есть среднее значение интенсивности отказов изделий. В дальнейшем под аргументом t будет пониматься время работы лидирующих изделий.

Связь среднего параметра потока отказов с характеристиками надежности невосстанавливаемых изделий. Математическое ожидание числа отказов n₁(t)за время работы одного невосстанавливаемого изделия равно вероятности отказа этого изделия:

Поскольку изделие не восстанавливаемое, n₁(t) ≤ 1. Соотношение (4.26) следует из определения вероятности отказа:

Для всехN(t)изделий, работавших в момент времени t, число отказов на интервале Δt:

где 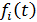–плотность вероятности отказа i-го изделия в момент t (рис. 4.7).

Число работоспособных изделий в момент t в соответствии с соотношениями (4.26) и (4.27), где q _i(t) = 1 – p _i(t):

С учетом (4.27) и (4.28) выражение (4.25) можно переписать в следующем виде:

Наработка изделия 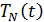к моменту времени t определяется выражением

Поэтому средний параметр потока отказов для рассматриваемой схемы функционирования невосстанавливаемыхизделий в соответствии с (4.28). (4.30) имеет следующее математическое выражение:

При t = 0 оказывается q(0)= 0 и 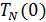= 0. Неопределенность (4.31) можно раскрыть, используя правило Лопиталя.Согласно ему, начальное значение параметра потока отказов равно начальному значению интенсивности отказов изделия:

При t → ∞из (4.31) следует:

т.е. средний параметр потока отказов с возрастанием времени процесса функционирования асимптотически стремится к установившемуся значению, равному обратной величине средней наработки до отказа.

Для изделий с постоянной интенсивностью отказов λ(t) = λ, для всех t

(0 ≤ t≤ ∞)из (4.31) имеет место

т.е. параметр потока отказов в этом случае равен интенсивности отказов на всем диапазоне изменения времени 0 – 0,005·1000 ) = 0,5 – 0,0034 ≈ 0,5.

Возьмем λ = 0,0005 1/ч. Тогда

Если планируется использование изделий до момента t₀при условии, что они уже наработали безотказно время 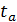, то в (4.65) следует использовать условные вероятности, исходя из соотношения (2.18).

При этом, если t −планируемая наработка лидирующего изделия, то из (2.18) и (4.65) имеем

где 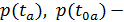исходная вероятность безотказной работы соответственно лидирующего изделия и изделия с минимальной наработкой; p(t),p(t₀_b) − вероятность безотказной работы до планируемой наработки соответственно лидирующего изделия и изделия с максимальной наработкой.

Зависимости (4.25), (4.38) и (4.45) позволяют определить среднее значение параметров надежности по парку однотипных изделий с распределенной наработкой. Поэтому среднее значение параметра потока отказов можно выразить также в виде первообразной функции

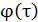
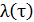
|где — плотность распределения наработки изделия для момента τ; — интенсивность отказов.

В случае равномерной плотности распределения 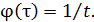Отсюда имеем

Таким образом, если известна функция λ(t), то можно просто вычислить значение 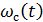и по (4.49), так как в процессе эксплуатации для многих типов изделий ведется учет их наработки и, следовательно, легко получить плотность распределения .

Контрольные вопросы

1. Какими параметрами характеризуется схема надежности восстанавливаемых деградирующих изделий?

2. Как определить среднее число отказов (восстановлений) изделий с полным восстановлением?

3. Какой величиной характеризуется среднее число отказов за единицу времени?

5. Как определить среднюю наработку на отказ и среднее число отказов?

6. Как определить среднюю вероятность отказапри равномерно распределенной наработке?

ГЛАВА 5

Последнее изменение этой страницы: 2019-05-04; Просмотров: 379; Нарушение авторского права страницы

Источник

1.1 Вероятность безотказной работы

Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки не произойдет ни одного отказа.
Вероятность безотказной работы обозначается как P(l), которая определяется по формуле (1.1):

Рис.2.1. График изменения вероятности безотказной работы P(l)в зависимости от наработки

Основными достоинствами использования данного показателя при расчетах является два фактора: во-первых, вероятность безотказной работы охватывает все факторы, влияющие на надежность элементов, позволяя достаточно просто судить о его надежности, т.к. чем больше величина P ( l ), тем выше надежность; во-вторых, вероятность безотказной работы может быть использована в расчетах надежности сложных систем, состоящих из более чем одного элемента.

1.2 Вероятность отказа

Вероятностью отказа называют вероятность того, что при определенных условиях эксплуат ации, в предела х заданной наработки произойдет хотя бы один отказ.
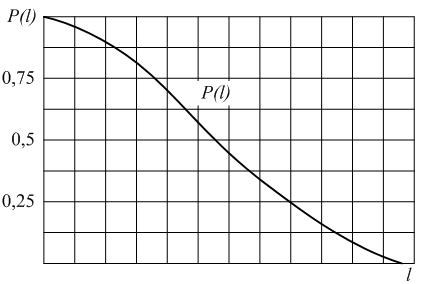
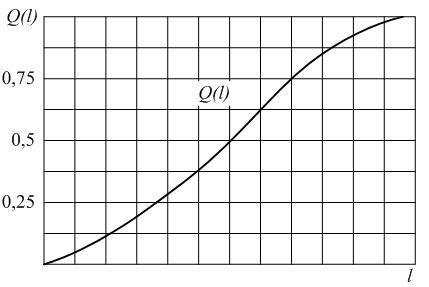
Вероятность отказа обозначается как Q(l), которая определяется по формуле (1.2):

В начале эксплуатации исправного локомотива Q (0) = 0, так как при пробеге l = 0 вероятность того, что хотя бы один элемент откажет, принимает минимальное значение – 0. С ростом пробега l вероятность отказа Q ( l ) будет увеличиваться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность отказа будет стремиться к единице Q ( l →∞ ) = 1. Таким образом в процессе наработки величина вероятности отказа изменяется в пределах от 0 до 1. Характер изменения вероятности отказа в функции пробега показан на рис. 1.2. Вероятность безотказной работы и вероятность отказа являются событиями противоположными и несовместимыми.

Рис.2.2. График изменения вероятности отказа Q(l) в зависимости от наработки

1.3 Частота отказов

Частота отказов – это отношение числа элементов в единицу времени или пробега отнесенного к первоначальному числу испытуемых элементов. Другими словами частота отказов является показателем, характеризующим скорость изменения вероятности отказов и вероятности безотказной работы по мере роста длительности работы.
Частота отказов обозначается как 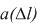и определяется по формуле (1.3):

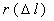
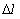
где – количество отказавших элементов за промежуток пробега .
Данный показатель позволяет судить по его величине о числе элементов, которые откажут на каком-то промежутке времени или пробега, также по его величине можно рассчитать количество требуемых запасных частей.
Характер изменения частоты отказов в функции пробега показан на рис. 1.3.

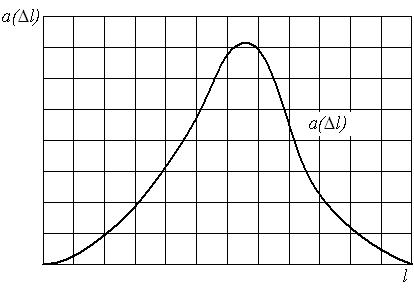
Рис. 1.3. График изменения частоты отказов в зависимости от наработки

1.4 Интенсивность отказов

Интенсивность отказов представляет собой условную плотность возникновения отказа объекта, определяемую для рассматриваемого момента времени или наработки при условии, что до этого момента отказ не возник. Иначе интенсивность отказов – это отношение числа отказавших элементов в единицу времени или пробега к числу исправно работающих элементов в данный отрезок времени.
Интенсивность отказов обозначается как 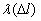и определяется по формуле (1.4):

где

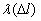
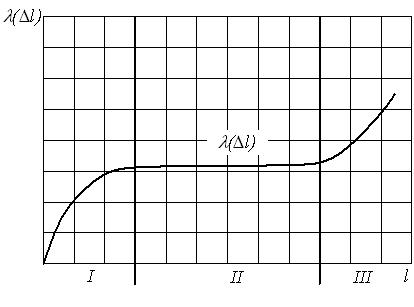
Как правило, интенсивность отказов является неубывающей функцией времени. Интенсивность отказов обычно применяется для оценки склонности к отказам в различные моменты работы объектов.
На рис. 1.4. представлен теоретический характер изменения интенсивности отказов в функции пробега.

Рис. 1.4. График изменения интенсивности отказов в зависимости от наработки

На графике изменения интенсивности отказов, изображенном на рис. 1.4. можно выделить три основных этапа отражающих процесс экс-плуатации элемента или объекта в целом.
Первый этап, который также называется этапом приработки, характеризуется увеличением интенсивности отказов в начальный период эксплуатации. Причиной роста интенсивности отказов на данном этапе являются скрытые дефекты производственного характера.
Второй этап, или период нормальной работы, характеризуется стремлением интенсивности отказов к постоянному значению. В течение этого периода могут возникать случайные отказы, в связи с появлением внезапной концентрации нагрузки, превышающей предел прочности элемента.
Третий этап, так называемый период форсированного старения. Характеризуется возникновением износовых отказов. Дальнейшая эксплуатация элемента без его замены становится экономически не рациональной.

1.5 Средняя наработка до отказа

Средняя наработка до отказа – это средний пробег безотказной работы элемента до отказа.
Средняя наработка до отказа обозначается как L₁ и определяется по формуле (1.5):

где l_i – наработка до отказа элемента; r_i – число отказов.
Средняя наработка до отказа может быть использована для предварительного определения сроков ремонта или замены элемента.

1.6 Среднее значение параметра потока отказов

Среднее значение параметра потока отказов характеризует среднюю плотность вероятности возникновения отказа объекта, определяемая для рассматриваемого момента времени.
Среднее значение параметра потока отказов обозначается как W _ср и определяется по формуле (1.6):

1.7 Пример расчета показателей безотказности

Исходные данные.
В течение пробега от 0 до 600 тыс. км., в локомотивном депо произведен сбор информации по отказам ТЭД. При этом количество исправных ТЭД в начале периода эксплуатации составляло N 0 = 180 шт. Суммарное количество отказавших ТЭД за анализируемый период составило ∑r(600000) = 60. Интервал пробега принять равным 100 тыс. км. При этом количество отказавших ТЭД по каждому участку составило: 2, 12, 16, 10, 14, 6.

Требуется.
Необходимо рассчитать показатели безотказности и построить их зависимости изменения во времени.

Сначала необходимо заполнить таблицу исходных данных так, как это показано в табл. 1.1.

Первоначально по уравнению (1.1) определим для каждого участка пробега величину вероятности безотказной работы. Так, для участка от 0 до 100 и от 100 до 200 тыс. км. пробега вероятность безотказной работы составит:

Далее, используя зависимость (1.2) произведем расчет вероятности отказа ТЭД.

Произведем расчет частоты отказов по уравнению (1.3).

Далее по уравнению (1.4) произведем расчет интенсивности отказов ТЭД в зависимости от наработки.
Первоначально рассчитаем среднее количество работоспособных ТЭД на участке от 0 до 100 тыс. км. пробега:

Тогда интенсивность отказов на участке 0-100 тыс.км. будет равна:

Аналогичным образом определим величину интенсивности отказов для интервала 100-200 тыс. км.

По уравнениям (1.5 и 1.6) определим среднюю наработку до отказа и среднее значение параметра потока отказов.

Систематизируем полученные результаты расчета и представим их в виде таблицы (табл. 1.2.).

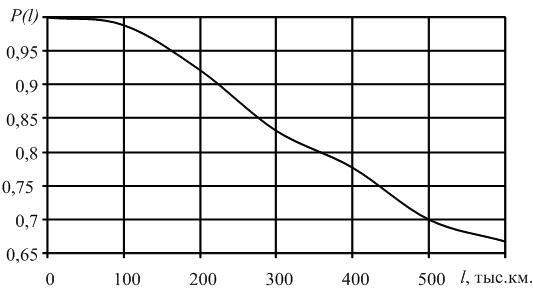
Приведем характер изменения вероятности безотказной работы ТЭД в зависимости от пробега (рис. 1.5.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности безотказной работы примет максимальное значение – 1.

Рис. 1.5. График изменения вероятности безотказной работы в зависимости от наработки

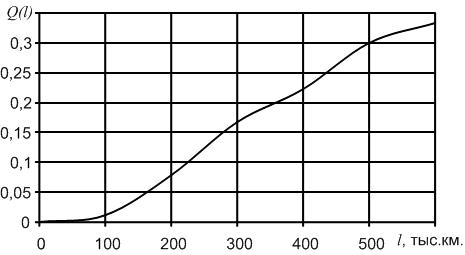
Приведем характер изменения вероятности отказа ТЭД в зависимости от пробега (рис. 1.6.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности отказа примет минимальное значение – 0.

Рис. 1.6. График изменения вероятности отказа в зависимости от наработки

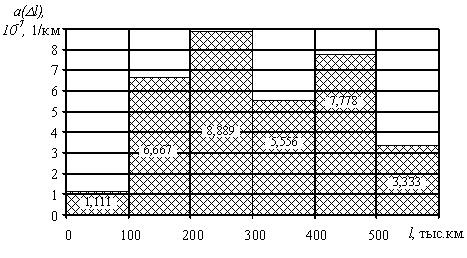
Приведем характер изменения частоты отказов ТЭД в зависимости от пробега (рис. 1.7.).

Рис. 1.7. График изменения частоты отказов в зависимости от наработки

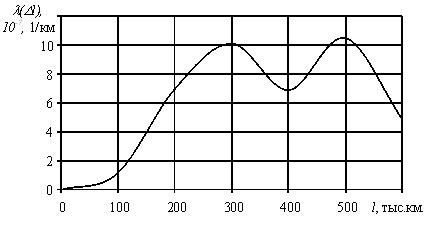
На рис. 1.8. представлена зависимость изменения интенсивности отказов от наработки.

Рис. 1.8. График изменения интенсивности отказов в зависимости от наработки

2.1 Экспоненциальный закон распределения случайных величин

Экспоненциальный закон достаточно точно описывает надежность узлов при внезапных отказах, имеющих случайный характер. Попытки применить его для других типов и случаев отказов, особенно постепенных, вызванных износом и изменением физико-химических свойств элементов показали его недостаточную приемлемость.

Исходные данные.
В результате испытания десяти топливных насосов высокого давления получены наработки их до отказа: 400, 440, 500, 600, 670, 700, 800, 1200, 1600, 1800 ч. Предполагая, что наработка до отказа топливных насосов подчиняется экспоненциальному закону распределения.

Во-первых, определим величину средней наработки топливных насосов до отказа по уравнению:

Затем рассчитываем величину интенсивности отказов:

Величина вероятности безотказной работы топливных насосов при наработке 500 ч составит:

Вероятность отказа в промежутке между 800 и 900 ч. работы насосов составит:

2.2 Закон распределения Вэйбулла-Гнеденко

Закон распределения Вейбулла-Гнеденко получил широкое распространение и используется применительно к системам, состоящим из рядов элементов, соединенных последовательно с точки зрения обеспечения безотказности системы. Например, системы, обслуживающие дизель-генераторную установку: смазки, охлаждения, питания топливом, воздухом и т.д.

Исходные данные.
Время простоя тепловозов в неплановых ремонтах по вине вспомогательного оборудования подчиняется закону распределения Вейбулла-Гнеденко с параметрами b=2 и a=46.

Требуется.
Необходимо определить вероятность выхода тепловозов из неплановых ремонтов после 24 ч. простоя и время простоя, в течение которого работоспособность будет восстановлена с вероятностью 0,95.

Найдем вероятность восстановления работоспособности локомотива после простоя его в депо в течение суток по уравнению:

Для определения времени восстановления работоспособности локомотива с заданной величиной доверительной вероятности также используем выражение:

2.3 Закон распределения Рэлея

Закон распределения Рэлея используется в основном для анализа работы элементов, имеющих ярко выраженный эффект старения (элементы электрооборудования, различного рода уплотнения, шайбы, прокладки, изготовленные из резиновых или синтетических материалов).

Исходные данные.
Известно, что наработки контакторов до отказа по параметрам старения изоляции катушек можно описать функцией распределения Рэлея с параметром S = 260 тыс.км.

Требуется.
Для величины наработки 120 тыс.км. необходимо определить вероятность безотказной работы, интенсивность отказов и среднюю наработку до первого отказа катушки электромагнитного контактора.

3.1 Основное соединение элементов

Система, состоящая из нескольких независимых элементов, связанных функционально таким образом, что отказ любого из них вызывает отказ системы, отображается расчетной структурной схемой безотказной работы с последовательно соединенными событиями безотказной работы элементов.

Исходные данные.
Нерезервированная система состоит из 5 элементов. Интенсивности их отказов соответственно равны 0,00007; 0,00005; 0,00004; 0,00006; 0,00004 ч-1

Требуется.
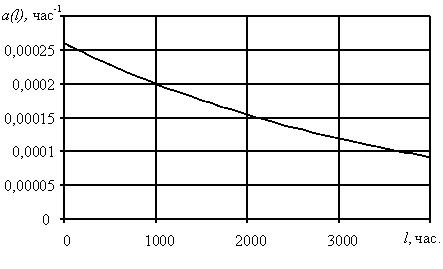
Необходимо определить показатели надежности системы: интенсивность отказов, среднее время наработки до отказа, вероятность безотказной работы, частота отказов. Показатели надежности P(l) и a(l) получить в интервале от 0 до 1000 часов с шагом в 100 часов.

Вычислим интенсивность отказа и среднюю наработку до отказа по следующим уравнениям:

Значения вероятности безотказной работы и частоты отказов получим, используя уравнения приведенные к виду:

Результаты расчета P(l) и a(l) на интервале от 0 до 1000 часов работы представим в виде табл. 3.1.

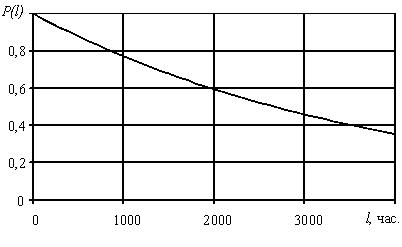
Графическая иллюстрация P(l) и a(l) на участке до средней наработки до отказа представлена на рис. 3.1, 3.2.

Рис. 3.1. Вероятность безотказной работы системы.

Рис. 3.2. Частота отказов системы.

3.2 Резервное соединение элементов

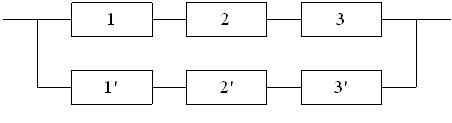
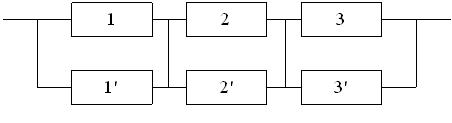
Исходные данные.
На рис. 3.3 и 3.4 показаны две структурные схемы соединения элементов: общего (рис. 3.3) и поэлементного резервирования (рис. 3.4). Вероятности безотказной работы элементов соответственно равны P1(l) = P ’1(l) = 0,95; P2(l) = P’2(l) = 0,9; P3(l) = P ’3(l) = 0,85.

Требуется.
Необходимо рассчитать надежность двух систем.

Рис. 3.3. Схема системы с общим резервированием.

Рис. 3.4. Схема системы с поэлементным резервированием.

Вероятность безотказной работы блока из трех элементов без резервирования рассчитаем по выражению:

Вероятность безотказной работы той же системы при общем резервировании (рис. 3.3) составит:

Вероятности безотказной работы каждого из трех блоков при поэлементном резервировании (рис. 3.4) будут равны:

Вероятность безотказной работы системы при поэлементном резервировании составит:

Таким образом, поэлементное резервирование дает более существенное увеличение надежности (вероятность безотказной работы возросла с 0,925 до 0,965, т.е. на 4%).

Исходные данные.
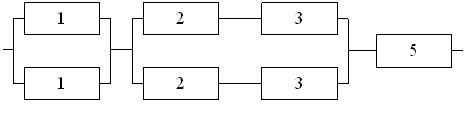
На рис. 3.5 представлена система с комбинированным соединением элементов. При этом вероятности безотказной работы элементов имеют следующие значения: P1=0,8; Р2=0,9; Р3=0,95; Р4=0,97.

Требуется.
Необходимо определить надежность системы. Также необходимо определить надежность этой же системы при условии, что резервные элементы отсутствуют.

Рис.3.5. Схема системы при комбинированном функционировании элементов.

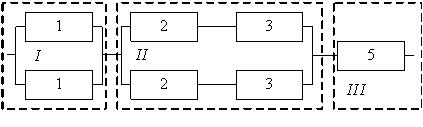
Для расчета в исходной системе необходимо выделить основные блоки. В представленной системе их три (рис. 3.6). Далее рассчитаем надежность каждого блока в отдельности, а затем найдем надежность всей системы.