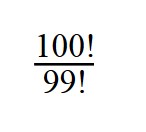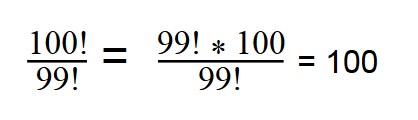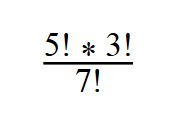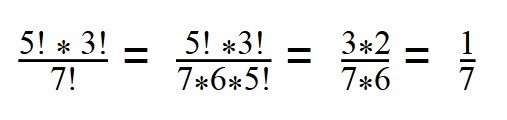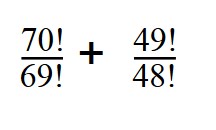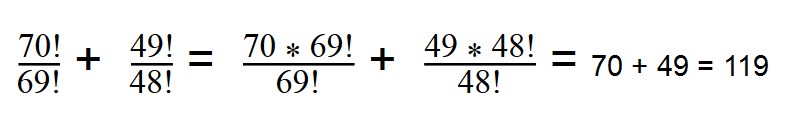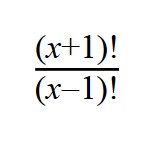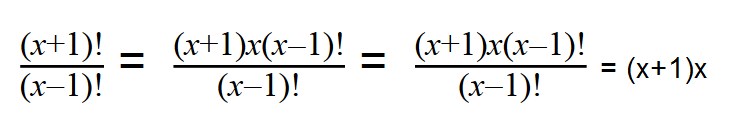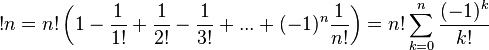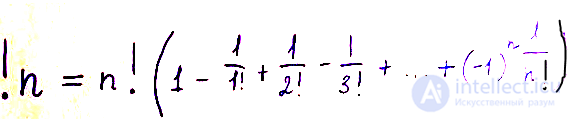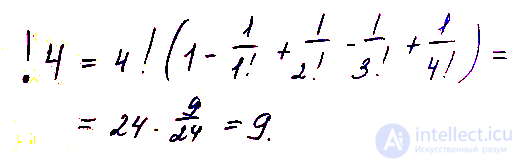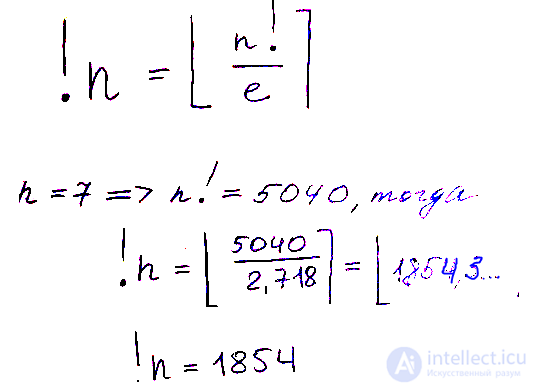субфакториал трех чему равен
Субфакториал и число Стирлинга
Когда в своей работе или учебе столкнетесь с теорией вероятности или комбинаторикой, Вам пригодятся эти формулы.
Онлайн калькуляторы( на 29 сентября 2017 года)
Число Стирлинга второго порядка
Числа Стирлинга второго рода, которые обозначают количество неупорядоченных разбиений множества из n элементов на k непустых подмножеств, вычисляются по рекуррентной формуле
n» src=»https://img.abakbot.ru/cgi-bin/mathtex.cgi?k%3En» style=»width: 41px; height: 11px;» />
Субфакториал
при начальном значении
| n | Dn |
|---|---|
| 0 | 1 |
| 1 | 0 |
| 2 | 1 |
| 3 | 2 |
| 4 | 9 |
| 5 | 44 |
| 6 | 265 |
| 7 | 1854 |
| 8 | 14833 |
| 9 | 133496 |
| 10 | 1334961 |
Число различных разбиений целого числа на целые слагаемые
Количество разбиений Pm(n) в некоторых случаях легко рассчитать самим.
Два слагаемых 1+4 или 2+3
Три слагаемых 3+1+1 или 2+2+1
Четыре слагаемых 2+1+1+1
Пять слагаемых 1+1+1+1+1
P 5 (1)=P 5 (4)=P 5 (5)=1
P 5 (2)=P 5 (3)=2
В общем случае числа Pm(n) находятся как коэффициенты разложения функции
Субфакториал
Субфакториал числа n (обозначение: !n) определяется как количество беспорядков порядка n, то есть перестановок порядка n без неподвижных точек. Название субфакториал происходит из аналогии с факториалом, определяющим общее количество перестановок.
В частности, !n есть число способов положить n писем в n конвертов (по одному в каждый), чтобы ни одно не попало в соответствующий конверт (т. н. Задача о письмах).
Содержание
Явная формула
Субфакториал можно вычислить с помощью принципа включения-исключения:
Другие формулы
Таблица значений
Свойства
Полезное
Смотреть что такое «Субфакториал» в других словарях:
Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия
Число Стирлинга первого рода — Числа Стирлинга первого рода количество перестановок из n предметов, имеющие ровно k циклов. Содержание 1 Определение 2 Рекуррентное соотношение 3 Пример 4 Свойст … Википедия
Числа Стирлинга первого рода — (без знака) количество перестановок порядка n с k циклами. Содержание 1 Определение 2 Рекуррентное соотношение 3 … Википедия
Четыре четвёрки — Четыре четверки математическая головоломка по поиску простейшего математического выражения для каждого целого числа от 0 до некоторого максимума, используя лишь общие математические символы и цифры четыре (никакие другие цифры не допускаются).… … Википедия
Факториал
Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
Число должно быть целое и положительное:
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Формулы и свойства факториала
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
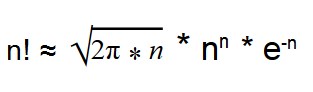 |
Рекуррентная формула
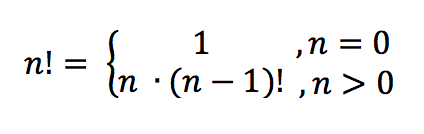 |
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
Deranged! Комбинаторика: вычислить субфакториал
Фактически, то же самое рекуррентное отношение верно для факториала, но для субфакториала мы начинаем с:
(Для факториала у нас, конечно, 1! = 1. )
правила
Результат должен быть точным целым числом (в частности, вы не можете приблизить результат с научной нотацией).
Вы можете написать программу или функцию и использовать любой из стандартных методов получения ввода и предоставления вывода.
Тестовые случаи
Число байтов предполагает кодировку UTF-16 с BOM.
Это определяет функцию, f которая принимает одно целое число и выводит другое целое число при повороте на 90 градусов влево. Это работает для произвольно больших входов.
Учитывая, что это Funciton, он даже достаточно быстрый (n = 20 занимает около 14 секунд на TIO). Основное замедление происходит из-за двойной рекурсии, поскольку я не думаю, что интерпретатор Funciton автоматически запоминает функции.
К сожалению, некоторые моноширинные шрифты неправильно моноширируют ♭ и / или не вставляют небольшие пропуски между строками. Вот скриншот кода от TIO во всей его красе:
Я думаю, что можно было бы еще немного поиграть в это, например, изменив условие с >0 на и поменяв местами условные ветви, чтобы я мог повторно использовать числовой литерал, или, возможно, используя совершенно другую формулу, но я вполне доволен тем, насколько он компактен.
объяснение
Это заголовок функции, который выдает вход функции n по присоединенной строке. Это немедленно достигает T-перехода, который просто дублирует значение.
Если условие было выполнено, то будет использоваться другое значение. Давайте посмотрим на путь, который ведет к этой ветви. (Обратите внимание, что оценка Funciton на самом деле ленива, так что эта ветвь никогда не будет оцениваться, если она не нужна, что делает рекурсию возможной в первую очередь.)
В другой ветви мы сначала вычисляем n-1, а затем дважды разделяем путь, чтобы получить три копии значения (одну для коэффициента повторения, одну для первого субфакториала, последнюю для n-2 ).
Субфакториал в математике, понятие и применение кратко
субфакториал числа n (обозначение: !n) определяется как количество беспорядков порядка n, то есть перестановок порядка n без неподвижных точек. Название субфакториал происходит из аналогии с факториалом, определяющим общее количество перестановок.
В частности, !n есть число способов положить n писем в n конвертов (по одному в каждый), чтобы ни одно не попало в соответствующий конверт (т. н. Задача о письмах).
Явная формула
Субфакториал можно вычислить с помощью принципа включения-исключения:
Другие формулы
Таблица значений
!14 = 32 071 101 049
!15 = 481 066 515 734
!16 = 7 697 064 251 745
!17 = 130 850 092 279 664
!18 = 2 355 301 661 033 953
!19 = 44 750 731 559 645 106
!20 = 895 014 631 192 902 121
!21 = 18 795 307 255 050 944 540
последовательность A000166 в OEIS
Свойства субфакториала
1, 1, 3, 11, 53, 309, 2119, … (последовательность A000255 в OEIS)
Применение субфакториала
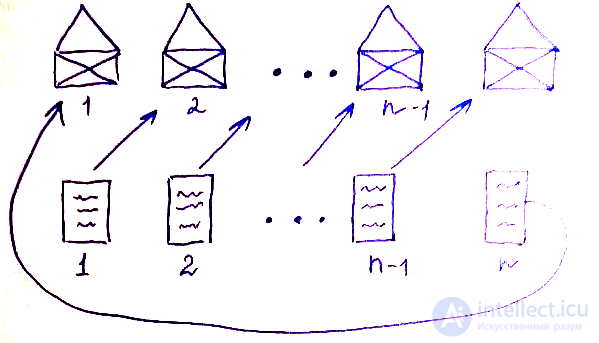
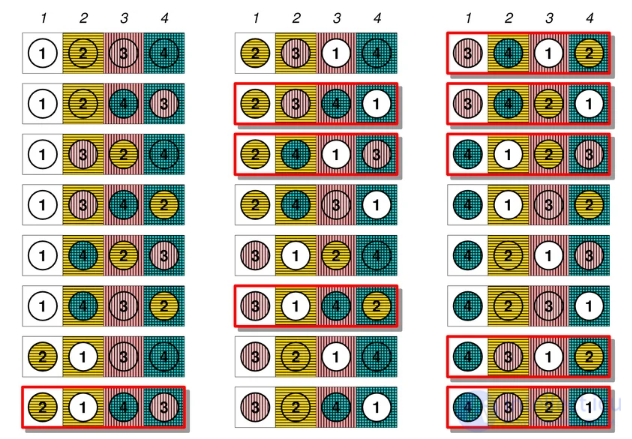
Итак, если факториал определяет количество перестановок, возможных в наборе из n объектов, то субфакториал характеризует количество беспорядков в таком же наборе. Проще всего понять, что такое факториал на жизненном примере. Возьмем некоторое количество писем и конвертов и пронумеруем их:
Вы уже, наверное, догадались, что именно субфакториал определит количество таких возможных перестановок, в комбинаторике называемых смещениями.
Формула для вычисления субфакториала сложностью не отличается:
Формула была выведена Николаем Бернулли еще в 1713 году.
Еще одна интерпретация задачи: профессор дал тест 4 студентам – 1, 2, 3 и 4 – и хочет, чтобы они оценили тесты друг друга. Конечно, ни один студент не должен оценивать свой собственный тест. Сколько существует способов, чтобы никто не получил обратно свой собственный тест для проверки?
Видно, что таких случаев 9, как и должно быть по формуле.Источник: https://upload.wikimedia.org/wikipedia/commons/thumb/f/f1/Derangement4.png/800px-Derangement4.png
Судя по формуле, субфакториал всегда меньше факториала, ведь в скобках величина всегда меньшая, чем 1/2 для n>3. Поразительно, но факториал и субфакторила лаконично связаны через постоянную Эйлера, и это действительно очень красиво:
Просто вычисляем ближайшее целое число к полученному результату
См. также
Из статьи мы узнали кратко, но емко про субфакториал