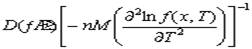свойства статистических оценок параметров распределения
Оценки параметров распределения и их свойства
Значение параметра, вычисленное по ограниченному объему ЭД, является случайной величиной, т. е. значение такой величины от выборки к выборке может меняться заранее не предвиденным образом. Следовательно, в результате обработки ЭД определяется не значение параметра T, а только лишь его приближенное значение – статистическая оценка параметра q. Получить статистическую оценку параметра теоретического распределения означает найти функцию от имеющихся результатов наблюдения, которая и даст приближенное значение искомого параметра. Различают два вида оценок – точечные и интервальные. Точечныминазывают такие оценки, которые характеризуются одним числом. При малых объемах выборки точечные оценки могут значительно отличаться от истинных значений параметров, поэтому их применяют при большом объеме выборки. Интервальныеоценки задаются двумя числами, определяющими вероятный диапазон возможного значения параметра. Эти оценки применяются для малых и для больших выборок. Рассмотрим вначале точечные оценки.
Применительно к каждому оцениваемому параметру закона распределения генеральной совокупности существует множество функций, позволяющих вычислить искомые значения. Например, оценку математического ожидания можно вычислить, взяв среднее арифметическое выборочных значений, половину суммы крайних членов вариационного ряда, средний член выборки и т.д. Указанные функции отличаются качеством оценок и трудоемкостью реализации.
Качество оценок характеризуется такими свойствами, как состоятельность, несмещенность, эффективность и достаточность [3, 5, 9].
Состоятельность характеризует сходимость по вероятности оценки q к истинному значению параметра T при неограниченном увеличении объема выборки n. Для состоятельности оценки достаточно, но не обязательно, чтобы математическое ожидание квадрата отклонения оценки от параметра M(T – q) 2 стремилось к нулю с увеличением объема выборки (здесь и далее символ М означает математическое ожидание). Свойство состоятельности проявляется при неограниченном увеличении n, а при небольших объемах ЭД наличие этого свойства еще недостаточно для применения оценки.
Несмещенность характеризует отсутствие систематических (в среднем) отклонений оценки от параметра при любом конечном, в том числе и малом, объеме выборки, т. е. M(q) = T. Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Не всегда наличие смещения плохо. Оно может быть существенно меньше погрешности регистрации значений параметра или давать дополнительную гарантию выполнения требований к значению параметра (если даже при положительном смещении оценка q меньше предельно допустимого значения, то несмещенное значение тем более будет отвечать этому условию). В таких ситуациях допустимо применение смещенных оценок, если они вычисляются проще, чем несмещенные. Но даже несмещенная оценка может быть удалена от истинного значения.
Эффективностьхарактеризует разброс случайных значений оценки около истинного значения параметра. Среди всех оценок следует выбрать ту, значения которой теснее сконцентрированы около оцениваемого параметра. Для многих применяемых способов оценивания выборочные распределения параметров асимптотически нормальны, поэтому часто мерой эффективности служит дисперсия оценки. В таком понимании эффективная оценка – это оценка с минимальной дисперсией. При неограниченном увеличении n эффективная оценка является и состоятельной. В случае оценивания одного параметра дисперсия несмещенной оценки отвечает условию Рао – Крамера,
где f(x, T) – плотность распределения варианты; п – количество наблюдений.
Сравнительная эффективность оценки с дисперсией Dk(q) измеряется коэффициентом эффективности
который не превышает единицы. Чем ближе коэффициент e к единице, тем эффективнее оценка. Отмеченное ограничение применимо и к дискретным распределениям, если вместо плотности распределения подставить в него функцию вероятности.
Достаточностьхарактеризует полноту использования информации, содержащейся в выборке. Другими словами, оценка q будет достаточной, если все другие независимые оценки на основе данной выборки не дают дополнительной информации об оцениваемом параметре. Эффективная оценка обязательно является и достаточной.
Рассмотренные свойства применимы также и к ЭД, которые характеризуются многомерными распределениями вероятностей.
Подходы к формированию оценок разработаны в теории несмещенных оценок , предложенной А. Н. Колмогоровым и С. Рао. В данной теории предполагается известным с точностью до параметра T вид функции плотности распределения наблюдаемой величины f(x, Т). Вид распределения устанавливается исходя из априорных соображений, например, на основе общепринятых суждений о характере безотказной работы технических средств. Тогда задача сводится к нахождению такой функции от результатов наблюдений, которая дает несмещенную и эффективную оценку.
Статистические оценки параметров распределения
Вы будете перенаправлены на Автор24
Распределения в математической статистике характеризуется многими статистическими параметрами. Оценка неизвестных параметров распределения на основе различных данных выборки позволяет построить распределения случайной величины.
Статистические оценки можно разделить на несмещенные, смещенные, эффективные и состоятельные.
Готовые работы на аналогичную тему
Генеральная и выборочная средние
Величины генерального и выборочного среднего можно найти по следующим формулам:
С этим понятием связано такое понятие как отклонение от средней. Данная величина находится по следующей формуле:
Среднее отклонение обладает следующими свойствами:
Среднее значение отклонения равно нулю.
Генеральная, выборочная и исправленная дисперсии
Еще одними из основных параметров является понятие генеральной и выборочной дисперсии:
Генеральная дисперсия:
Выборочная дисперсия:
С этими понятия связаны также генеральная и выборочная средние квадратические отклонения:
В качестве оценки генеральной дисперсии вводится понятие исправленной дисперсии:
Также вводится понятие исправленного стандартного отклонения:
Пример решения задачи
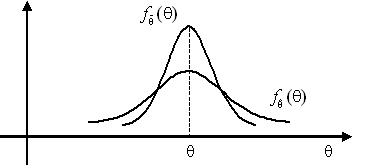
Генеральная совокупность задана следующей таблицей распределения:
Найдем для нее генеральное среднее, генеральную дисперсию, генеральное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.
Для решения этой задачи для начала сделаем расчетную таблицу:
Найдем генеральную дисперсию по формуле:
Генеральное среднее квадратическое отклонение:
Исправленное среднее квадратическое отклонение:
Математическая статистика
Точечные оценки
Свойства точечных оценок
Пусть x1. xn – выборка наблюдений случайной величины X, имеющей распределение FX(x). При проведении ряда статистических исследований вид функции распределения наблюдаемой случайной величины зачастую предполагается известным (например, случайная величина имеет нормальное или биномиальное распределение). Неизвестными же являются параметры этого распределения.
Одной из задач математической статистики является оценка неизвестных параметров распределения наблюдаемой случайной величины X по выборке x1. xn её наблюдений.
Параметром θ∈Θ распределения FX(x) случайной величины X называется любая числовая характеристика этой случайной величины (математическое ожидание, дисперсия и т.п.) или любая константа, явно входящая в выражение для функции распределения FX(x).
Напомним, что любая выборка наблюдений x1. xn является реализацией случайной выборки X1. Xn. Статистикой Z в математической статистике называется произвольная функция случайной выборки, не зависящая от неизвестных параметров распределения:
В связи с тем, что статистика Z является функцией случайных аргументов, Z является случайной величиной. Для каждой реализации x1. xn случайной выборки X1. Xn получим соответствующую ей реализацию z статистики Z:
называемую выборочным значением статистики Z.
Основные свойства точечных оценок.
1. Состоятельность (Consistency)
$\forall \varepsilon >0\ \ \ P\left( \left| <<<\tilde<\theta >>>_
3. Эффективность (Efficiency)
Для оценки параметра θ может быть предложено несколько несмещённых оценок. Вследствие несмещённости различные реализации этих оценок будут группироваться относительно их математического ожидания, равного θ, однако разброс этих значений может быть различным. Как известно, мерой разброса значений случайной величины относительно математического ожидания является её дисперсия.
Оценка параметра θ, имеющая минимально возможную дисперсию среди всех оценок, называется эффективной оценкой параметра θ. В математической статистике наряду с термином «эффективная оценка» используют и другие: «несмещённая оценка с минимальной дисперсией», «оптимальная оценка».
При выполнении условий регулярности каждый элемент независимой случайной выборки X1. Xn вносит равный вклад в информацию Фишера In(θ), т.е.
где I(θ) – количество информации по Фишеру о параметре θ, содержащееся в одном выборочном наблюдении.
Величина информации по Фишеру зависит от вида распределения генеральной совокупности X. Так, выборки, полученные из генеральных совокупностей с разными распределениями (например, нормальным и биномиальным) будут содержать различное количество информации о неизвестных математическом ожидании или дисперсии.
Чем больше информации по Фишеру о параметре θ содержится в выборочных наблюдениях, тем меньший разброс имеют реализации эффективной оценки этого параметра, а следовательно, являются более точными.
Формально информация по Фишеру о параметре θ, содержащаяся в одном выборочном наблюдении из генеральной совокупности с функцией плотности распределения fX(x, θ), рассчитывается по формуле
называется вкладом выборки.
Тема 3.3. Статистические оценки параметров распределения
Свойства статистических оценок
Методы нахождения точечных оценок
Интервальное оценивание параметров
Доверительный интервал для математического ожидании при известной дисперсии нормально распределённой генеральной совокупности.
Распределение хи-квадрат и распределение Стьюдента.
Доверительный интервал для математического ожидании случайные величины, имеющей нормальное распределение при неизвестной дисперсии.
Доверительный интервал для среднего квадратического отклонения нормального распределения.
Вентцель, Е.С. Теория вероятностей [Текст] / Е.С. Вентцель. – М.: Высшая школа, 2006. – 575 с.
П.1. Понятие оценки
Такие распределения, как биномиальное, показательное, нормальное, являются семействами распределений, зависящими от одного или нескольких параметров. Например, показательное распределение с плотностью вероятностей 
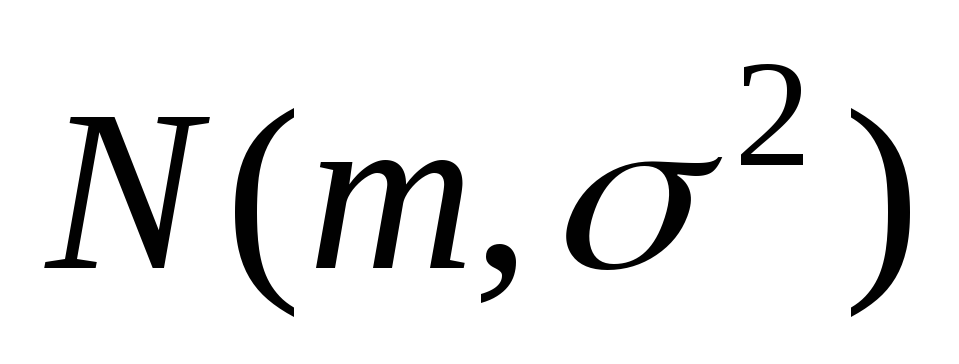
Пусть закон распределения генеральной совокупности определён с точностью до значений входящих в его распределение параметров 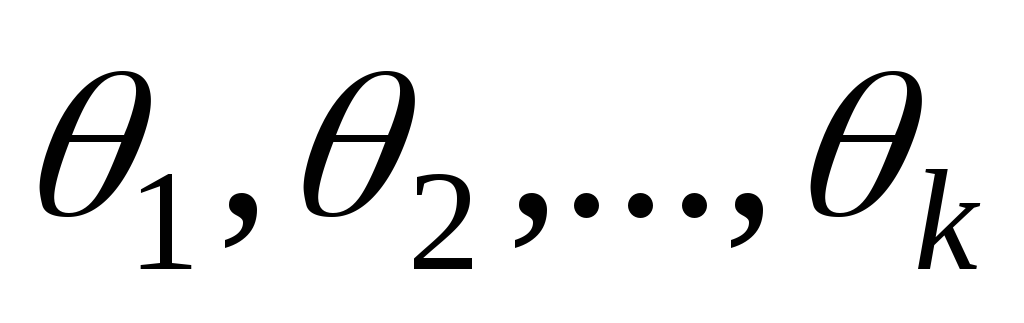



Статистической оценкой (в дальнейшем просто оценкой) 
Оценка 

Существует два вида оценок – точечные и интервальные.
Точечной называется оценка, определяемая одним числом. При малом числе наблюдений эти оценки могут приводить к грубым ошибкам. Чтобы избежать их, используют интервальные оценки.
Интервальной называется оценка, которая определяется двумя числами – концами интервала, в котором с заданной вероятностью заключена оцениваемая величина θ.
П. 2 Свойства статистических оценок
Величину 
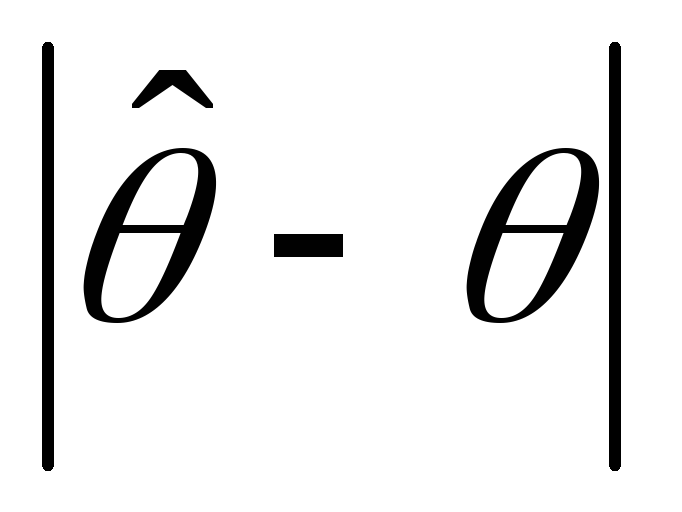
К оценке любого параметра предъявляется ряд требований, которым она должна удовлетворять, чтобы быть «близкой» к истинному значению параметра, т.е. быть в каком-то смысле «доброкачественной» оценкой. Качество оценки определяют, проверяя, обладает ли она свойствами несмещённости, эффективности и состоятельности.
Оценка 

Если равенство (1) не имеет места, то оценка 
Для некоторых задач математической статистики может существовать несколько несмещённых оценок. Обычно предпочтение отдают той, которая обладает наименьшим рассеянием (дисперсией).
Оценка 
Пусть D(

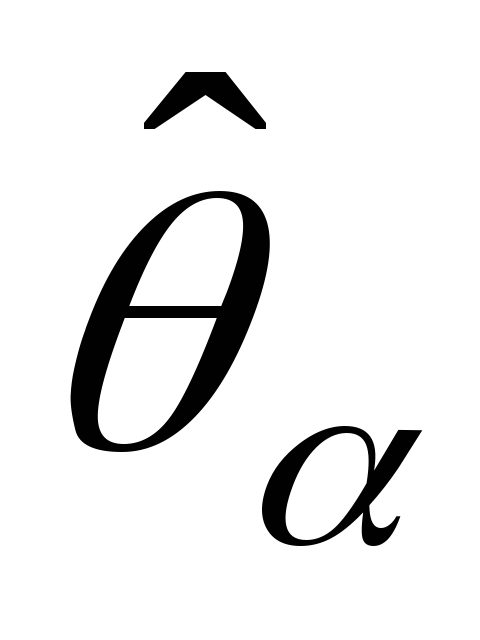


Ясно, что 




Замечание: Если оценка 


Оценка 


Состоятельность оценки 

Теорема 1. Выборочная средняя является несмещённой и состоятельной оценкой математического ожидания.
Теорема 2. Исправленная выборочная дисперсия является несмещённой и состоятельной оценкой дисперсии.
Теорема 3. Эмпирическая функция распределения выборки является несмещённой и состоятельной оценкой функции распределения случайной величины.
Основные свойства статистических характеристик параметров распределения
Получив статистические оценки параметров распределения (выборочное среднее, выбороч-ную дисперсию и т.д.), нужно убедиться, что они в достаточной степени служат приближе-нием соответствующих характеристик генеральной совокупности. Определим требования, которые должны при этом выполняться.
Убедимся, что 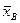
Будем рассматривать 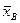
Но, поскольку каждая из величин Х1, Х2,…, Хп имеет такое же распределение, что и генеральная совокупность, а = М(Х), то есть М(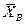
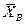
В отличие от выборочного среднего, выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности. Можно доказать, что
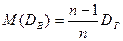
где DГ – истинное значение дисперсии генеральной совокупности. Можно предложить другую оценку дисперсии – исправленную дисперсию s², вычисляемую по формуле
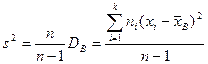
Такая оценка будет являться несмещенной. Ей соответствует исправленное среднее квадратическое отклонение
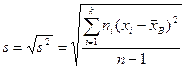
Определение 4. Оценка некоторого признака называется асимптотически несмещенной, если для выборки х1, х2, …, хп
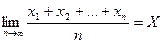
где Х – истинное значение исследуемой величины.