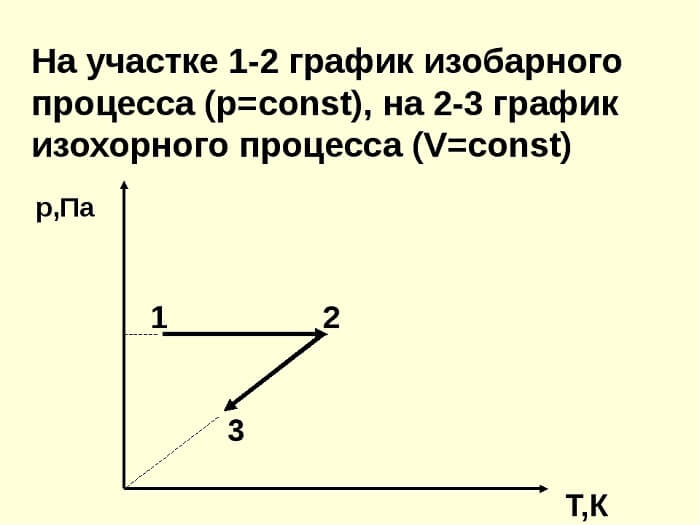
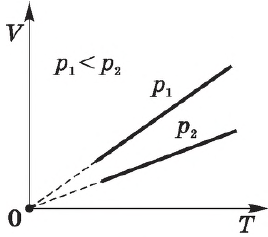
связь между параметрами для изохорного процесса имеет вид
Уравнение состояния идеального газа. Изопроцессы
Соотношение p = n k T – это формула, связывающая значение давления газа с его температурой и концентрацией молекул на единицу объема.
Значением N является количество молекул данного сосуда, N А – постоянной Авогадро, m – массой газа в емкости, М – молярной массой газа. Исходя из этого, формула примет вид:
Соотношение p V = ν R T = m M R T получило название уравнения состояния идеального газа.
Если имеется смесь невзаимодействующих газов, то формулу запишем как:
Еще в ХХ веке Б. Клапейрон получил уравнение, показывающее связь между давлением и температурой:
Впоследствии оно было записано Д.И. Менделеевым. Позже его назвали уравнением Клапейрона-Менделеева.
Задолго до получения уравнения состояния идеального газа на основе молекулярно-кинетической теории поведения газов изучались в различных условиях экспериментально. То есть уравнение p V = ν R T = m M R T служит обобщением всех опытных фактов.
При протекании процессов медленно, система находится в состоянии, близком к равновесному. Процесс получил название квазистатического.
Соотнеся с происхождением процессов в нашем времени, то его протекания нельзя считать медленными.
Обычное время для разрежения и сжатия газа сотни раз в секунду. Это рассматривается как квазистатический процесс. Они изображаются с помощью диаграммы состояний параметров, где каждая из точек показывает равновесное состояние.
Какой процесс называется изохорным
Какой процесс называется изохорным, условия протекания
Изохорным процессом называют термодинамический процесс, протекающий при условии постоянного объема.
Изохорный процесс можно наблюдать опытным путем. Для этого необходимо повышать или понижать температуру вещества в газообразном или жидком состоянии, находящегося в сосуде и сохраняющего стабильность объема. В случае, когда манипуляции производят с идеальным газом, его давление и температура будут изменяться прямо пропорционально, согласно закону Шарля. Для реальных газов данная закономерность не применима.
История возникновения теории, кто открыл, формула
Изучение изохорного процесса связывают с Гийомом Амонтоном. Работа ученого под названием «Парижские мемуары», написанная в 1702 году, посвящена исследованию характеристик газообразного вещества, помещенного в фиксированный объем, который составляет часть «воздушного термометра». Равновесие жидкости в данных условиях объясняется воздействием на нее давления газа, находящегося в сосуде, и атмосферного давления. Если температура среды повышается, показатели давления в резервуаре возрастают. При этом определенный объем жидкости вытесняется в выступающую трубку. Зависимость между такими характеристиками процесса, как температура и давление, представлена на рисунке.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В 1801 году были опубликованы два эссе исследователя Джона Дальтона с описанием эксперимента, результаты которого демонстрируют одинаковое расширение всех газов и паров при постоянном давлении и изменении температуры, когда начальная и конечная температура одинакова. В итоге был сформулирован закон Гей-Люссака. Ученый, в честь которого явление получило название, экспериментальным путем подтвердил одинаковое расширение различных газообразных веществ и вывел коэффициент, практически равный коэффициенту, полученному Дальтоном. Благодаря объединению данной закономерности с законом Бойля-Мариотта, был описан изохорный процесс.
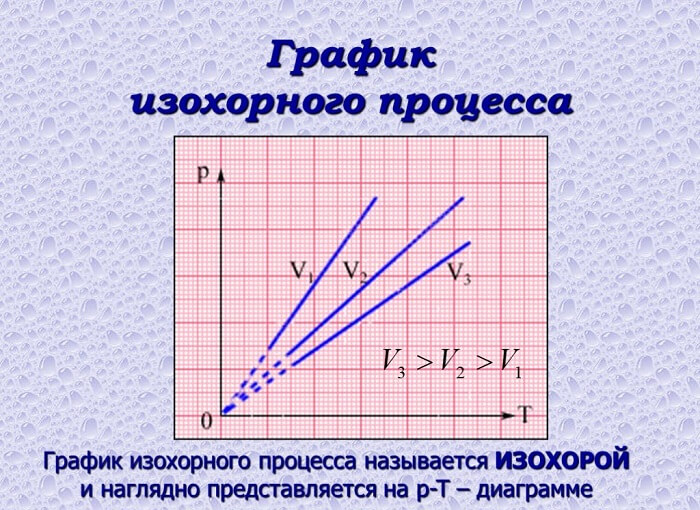
График изохорного процесса в идеальном газе
Зависимость характеристик при изохорном процессе можно представить схематично. График на диаграмме в системе координат будет иметь следующий вид:
В случае идеального газа графически изохорные процессы будут изображены следующим образом:
Первый закон термодинамики для изохорного процесса
В условиях термодинамического процесса формула элементарной работы имеет следующий вид:
Преобразование данного выражения позволит рассчитать величину полной работы процесса:
Изменение внутренней энергии для идеального газа рассчитывается по формуле:
\(\Delta U=\frac<2>\nu R\Delta T\)
где i представляет собой количество степеней свободы, зависящее от числа атомов, которыми обладает молекула газа. В качестве примера можно рассмотреть такие вещества:
Формула внутренней энергии выходит из понятия и уравнения теплоемкости, представляет собой следующее отношение:
где \(c_<\upsilon >^<\mu >\) является молярной теплоемкостью в условиях постоянного объема.
Расчет количества теплоты выполняют с помощью первого начала термодинамики в условиях термодинамического процесса:
Следует учитывать, что в условиях изохорного процесса газообразное вещество не выполняет работу. Исходя из этого, можно вывести формулу:
Согласно уравнению, газ получает теплоту. Она полностью расходуется, чтобы изменять внутреннюю энергию газообразного вещества.
Изменения термодинамических параметров в изохорном процессе
В условиях изохорного процесса наблюдается теплообмен с внешней средой. Данное явление называют изменением энтропии. Из его понятия следует уравнение:
где \(\delta Q\) является элементарным количеством теплоты.
Преобразуя уравнение для расчета количества теплоты в дифференциальный вид, получают следующую формулу:
где \(\nu\) является количеством вещества, а \(\nu c^<\mu >_<\upsilon >\) обозначает молярную теплоемкость в условиях постоянного объема.
Формула микроскопического изменения энтропии в условиях протекания изохорного процесса имеет вид:
Если проинтегрировать последнюю формулу, то расчет полного изменения энтропии выполняют таким образом:
В этой ситуации не представляется возможным вынести определение молярной теплоемкости в условиях стабильного объема за интеграл, так как оно представлено в виде функции, зависящей от температуры.
Применение эффекта изохорного процесса
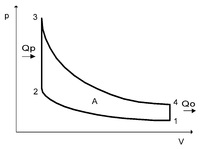
Идеальный цикл Отто приближенно воспроизведен в конструкции мотора внутреннего сгорания, работающего на бензине. Такты 2-3 и 4-1 при его функционировании представляют собой изохорные процессы. На выходе двигателя совершается работа. Она рассчитывается, как разность работ. К одной из них относят работу, производимую газообразным веществом над поршнем в процессе третьего такта или рабочего хода, к другой – работу, затраченную поршнем во время сжатия газа при втором такте. Таким образом, на примере двигателя, функционирующего, согласно принципу Отто, в системе принудительного сжигания смеси, газообразное вещество сжимается до 7-12 раз.
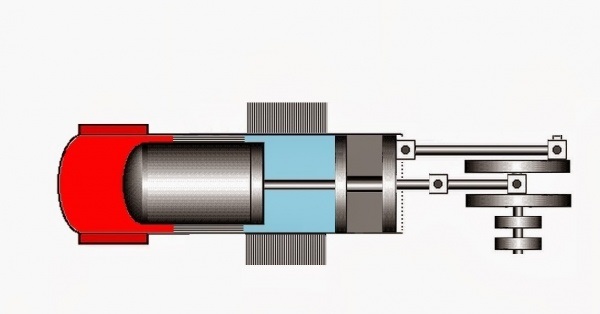
На рисунке изображен классический двигатель Стирлинга с конструкцией бета-типа, для которой характерно расположение рабочего и вытеснительного поршня в одном цилиндре.
Динамику цикла Отто можно представить в следующем виде:
Цикл Стирлинга также характеризуется наличием двух изохорных тактов. Процесс протекает при дооснащении конструкции двигателя Стирлинга регенератором. Во время прохождения газообразного вещества в одном направлении через наполнитель осуществляется передача тепла от рабочего тела к регенератору. Если газ проходит в обратную сторону, то тепловая энергия передается на рабочее тело. Идеальный цикл Стирлинга достигает обратимости и характеризуется теми же параметрами КПД, что и цикл Карно.
Блог об энергетике
энергетика простыми словами
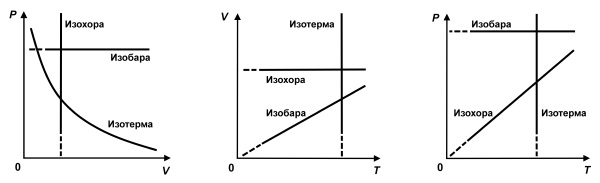
Основные термодинамические процессы
Основными процессами в термодинамике являются:
Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.
При исследовании термодинамических процессов определяют:
Изохорный процесс

При изохорном процессе выполняется условие v = const.
Из уравнения состояния идеального газа (pv = RT) следует:
т. е. давление газа прямо пропорционально его абсолютной температуре:
Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).
Количество теплоты, подведенной к рабочему телу в процессе 1-2 при cv = const определяется по формуле:
Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:
Изменение энтропии в изохорном процессе определяется по формуле:
Изобарный процесс
Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:
т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.
Работа будет равна:
Количество теплоты при cp = const определяется по формуле:
Изменение энтропии будет равно:
Изотермический процесс
При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:
т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.
Работа процесса будет равна:
Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:
При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.
Изменение энтропии равно:
Адиабатный процесс
Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:
В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.
Обозначим теплоемкость в адиабатном процессе через cад, и условие dq = 0 выразим следующим образом:
Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (cад = 0).
и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:
В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).
kвыхлопных газов ДВС = 1,33
Из предыдущих формул следует:
Техническая работа адиабатного процесса (lтехн) равна разности энтальпий начала и конца процесса (i1 – i2).
Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. В T, s-диаграмме он изображается вертикальной линией.
Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае ds > 0, и процесс называется реальным адиабатным процессом.
Политропный процесс
Политропным называется процесс, который описывается уравнением:
Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p, vи Tв любых двух точках на политропе:
Работа расширения газа в политропном процессе равна:
В случае идеального газа эту формулу можно преобразовать:
Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:
представляет собой теплоемкость идеального газа в политропном процессе.
При cv, k и n = const cn = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.
Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.
Графическое представление политропа в p, v координатах в зависимости от показателя политропа n.
pv 0 = const (n = 0) – изобара;
pv = const (n = 1) – изотерма;
p 0 v = const, p 1/∞ v = const, pv ∞ = const – изохора;
n > 0 – гиперболические кривые,
n По материалам моего конспекта лекций по термодинамике и учебника «Основы энергетики». Автор Г. Ф. Быстрицкий. 2-е изд., испр. и доп. — М. :КНОРУС, 2011. — 352 с.
Основы гидравлики
Уравнение изохорного процесса. Связь между параметрами в изохорном процессе по закону Шарля. Закон Гей-Люссака в изобарном процессе. Изменение внутренней энергии газа. Закон Бойля – Мариотта в изотермическом процессе. Уравнение состояния Клапейрона.
| Рубрика | Физика и энергетика |
| Вид | контрольная работа |
| Язык | русский |
| Дата добавления | 05.03.2013 |
| Размер файла | 416,0 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Уравнение изохорного процесса: v = const. Графически в p-v-диаграмме изохорный процесс изображается линией, параллельной оси давлений. Линии изохорного процесса в диаграмме состояния называется изохорой
Связь между параметрами в изохорном процессе подчиняется закону Шарля
И изохорном процессе вся подведенная теплота расходуется на изменение внутренней энергии тела. Для тела с произвольной массой вещества m имеем:
Так как в изохорном процессе нет изменения объема, то и работа по его изменению не совершается: W1-2 = 0.
Количество теплоты, подведенное в изохорном процессе, равно изменению внутренней энергии. Для произвольной массы вещества:
Уравнение изобарного процесса р= const.
Графически изобарный процесс в р-v-диаграмме изображается прямой линией, параллельной оси объемов. Линия изобарного процесса называется изобарой.
Связь между параметрами в изобарном процессе выражается законом Гей-Люссака:
Изменение внутренней энергии газа рассчитывается по формуле:
В изобарном процессе происходит изменение объема рабочего тела, следовательно, совершается работа, определяемая:
Для произвольной массы газа m формула работы примет:
Воспользовавшись первым законом термодинамики, можем рассчитать теплоту процесса (для 1 кг газа) по формуле:
При этом в термодинамике существует связь между изохорной cv и изобарной ср теплоемкостями. Связь устанавливается уравнением Майера:
Тогда выражение для определения количества теплоты для 1 кг газа примет вид:
для произвольной массы газа:
Таким образом, в изобарном процессе теплота расходуется на совершение работы и на изменение внутренней энергии рабочего тела.
3. Изотермический процесс
Уравнение изотермического процесса: Т= const или pv = const. Графически изотермический процесс в р-v-диаграмме изображается в виде равнобокой гиперболы что вытекает из уравнения pv = const, и называется изотермой.
Так как Т1 = Т2, изменение внутренней энергии газа в изотермическом процессе равно нулю:
Совершенная 1 кг газа работа в изотермическом процессе, c учетом того что RT = const, определяется следующим образом:
Для произвольной массы рабочего тела уравнение работы примет вид:
Графически в p-v диаграмме работа в процессе 1-2 определяется площадью под изотермой.
Теплота, участвующая в изотермическом процессе, определится соотношением:
Это означает что вся подведенная в изотермическом процессе теплота расходуется на совершение работы.
Уравнение адиабатного процесса имеет вид:
Графически адиабатный процесс на p-v-диаграмме изображается неравнобокой гиперболой, называемой адиабатой. Адиабата круче изотермы, так как к > 1.
Связь между параметрами процесса определяется, используя уравнение адиабаты и уравнение состояния газа pv = RT:
Изменение внутренней энергии для т кг вещества определяется по формуле:
Работа в адиабатном процессе, совершенная 1 кг газа, может быть определена из уравнения первого закона термодинамики:
Так как в адиабатном процессе q=0, то:
то есть работа расширения в адиабатном процессе совершается за счет уменьшения внутренней энергии газа.
Адиабатный процесс протекает без подвода теплоты, следовательно Q=0.
5. Политропный процесс
Уравнение политропного процесса имеет вид
Рассмотренные ранее процессы являются частными случаями иолитроппых процессов:
Показатель изотропы n можно определить, если известны два состояния политропном процесс
Графическое изображение политропного процесса в р-v-диа-грамме имеет вид кривой, которая называется политропой.
Соотношение параметров данного процесса можно получить, заменив в уравнениях адиабатного процесса показатель степени k на показатель n:
Изменение внутренней энергии в политропном процессе для произвольной массы вещества определяется по формуле
Работа изменения объема в политропном процессе для
1 кг рабочего тела равна
или, учитывая уравнение состояния Клапейрона,
Для произвольной массы газа
Количество теплоты в политропном процессе для m кг вещества определяется выражением, полученным в соответствии с первым законом термодинамики
изохорный шарль изобарный клапейрон
Размещено на Allbest.ru
Подобные документы
Закон сохранения энергии и первое начало термодинамики. Внешняя работа систем, в которых существенную роль играют тепловые процессы. Внутренняя энергия и теплоемкость идеального газа. Законы Бойля-Мариотта, Шарля и Гей-Люссака, уравнение Пуассона.
презентация [0 b], добавлен 25.07.2015
Определение и модель идеального газа. Микроскопические и макроскопические параметры газа и формулы для их расчета. Уравнение состояния идеального газа (уравнение Менделеева-Клайперона). Законы Бойля Мариотта, Гей-Люссака и Шарля для постоянных величин.
презентация [1008,0 K], добавлен 19.12.2013
презентация [227,0 K], добавлен 18.05.2011
Уравнение Менделеева-Клайперона, газовая постоянная. Отношение абсолютных давлений и температур. Нахождение количества теплоты произвольной массы газа в изобарном процессе. Состояние идеального газа. Работа в изотермическом и адиабатном процессах.
задача [333,3 K], добавлен 16.06.2012
Первый закон термодинамики. Обратимые и необратимые процессы. Термодинамический метод их исследования. Изменение внутренней энергии и энтальпии газа. Графическое изображение изотермического процесса. Связь между параметрами газа, его теплоемкость.
лекция [438,5 K], добавлен 14.12.2013
Изопроцессы, работа в термодинамике, первый закон термодинамики
Теория к заданию 8 из ЕГЭ по физике
Основное уравнение МКТ (давление газа)
Основное уравнение молекулярно-кинетической теории устанавливает связь между давлением идеального газа и средней кинетической энергией его молекул.
Вывод основного уравнения МКТ основывается на допущениях модели идеального газа и утверждении: давление газа является результатом ударов молекул о стенку сосуда.
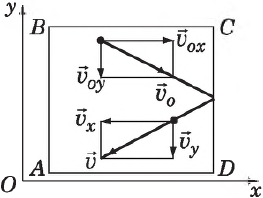
Поскольку вследствие хаотичности движения все направления равноправны, то
С другой стороны, известно, что квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат, поэтому:
Следовательно, давление на стенку сосуда равно:
Это основное уравнение молекулярно-кинетической теории. Это уравнение — первое количественное соотношение, полученное в МКТ.
Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.
Важно подчеркнуть, что здесь речь идет о средней кинетической энергии молекул газа. Это означает, что давление газа — величина, органически связанная с тем, что газ состоит из большого числа молекул. Нет смысла говорить о давлении, создаваемом несколькими молекулами. Давление газа — понятие, имеющее статистический характер (так называют понятия, имеющие смысл только для систем с очень большим числом частиц).
Абсолютная температура
Температура, как и давление, определяется средней кинетической энергией молекул идеального газа. Поэтому температура, как и давление, является статистической величиной (статистической называется величина, имеющая смысл только для систем, содержащих очень большое число частиц). Нельзя говорить о температуре одной или нескольких молекул.
Абсолютную шкалу температур ввел английский ученый У. Кельвин в 1850 г. Нулевая температура по абсолютной шкале (ее называют также шкалой Кельвина) соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.
Температура как мера кинетической энергии
Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.
Из полученного результата однозначно следует, что абсолютная температура есть мера средней кинетической энергии движения молекул.
Соотношение между температурой и кинетической энергией справедливо не только для разреженных газов (идеальных газов), но также для любых тел, подчиняющихся законам механики Ньютона. Оно справедливо и для жидкостей, и для твердых тел, атомы которых колеблются около положения равновесия.
Отсюда следует известный закон Авогадро: в равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Квадратный корень из этой величины называется средней квадратичной скоростью:
Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)
В результате получим:
Внутренняя энергия идеального одноатомного газа
Внутренняя энергия идеального одноатомного газа прямо пропорциональна его температуре.
Если воспользоваться уравнением Клапейрона-Менделеева, то выражение для внутренней энергии идеального газа можно представить в виде:
Число степеней свободы — это число возможных независимых направлений движения молекулы.
Формулы для внутренней энергии идеального газа можно обобщить:
Для идеальных газов внутренняя энергия зависит только от одного макроскопического параметра — температуры и не зависит от объема, т. к. потенциальная энергия равна нулю (объем определяет среднее расстояние между молекулами).
Для реальных газов потенциальная энергия не равна нулю. Поэтому внутренняя энергия в термодинамике в общем случае однозначно определяется параметрами, характеризующими состояние этих тел: объемом ($V$) и температурой ($Т$).
Изопроцессы в газах
Изопроцессами называются процессы, протекающие при неизменном значении одного из параметров: давления ($р$), объема ($V$), температуры ($Т$).
В идеальном газе эти процессы подчиняются газовым законам.
Газовыми законами называются количественные зависимости между двумя параметрами газа при фиксированном значении третьего параметра.
Закон Бойля-Мариотта
Закон Бойля-Мариотта — один из основных газовых законов, он описывает изотермические процессы в газе.
Процесс изменения состояния термодинамической системы при постоянной температуре называется изотермическим.
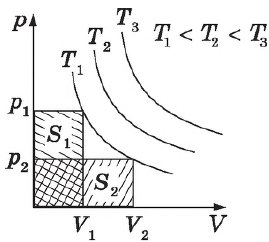
Для данной массы произведение давления газа на его объем постоянно, если температура газа не меняется.
Этот закон был экспериментально открыт английским ученым Р. Бойлем в 1662 г., в 1676 г. его сформулировал также французский ученый Э. Мариотт.
Закон Шарля
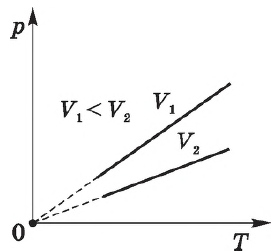
Закон был открыт французским физиком Ж. Шарлем в 1787 году.
Процесс изменения состояния термодинамической системы при постоянном объеме называется изохорным (от греч. hora — пространство).
Закон Шарля, как и другие газовые законы, является следствием уравнения состояния идеального газа:
Изохорный процесс используется в газовых термометрах постоянного объема.
Закон Гей-Люссака
Процесс изменения состояния термодинамической системы при постоянном давлении называется изобарным (от греч. baros — вес, тяжесть).
Закон открыт французским ученым Ж. Гей-Люссаком в 1802 г. и независимо от него Дж. Дальтоном в 1801 г.
Для газа данной массы отношение объема к температуре постоянно, если давление газа не меняется.
Эта зависимость графически изображается прямой, которая называется изобарой.