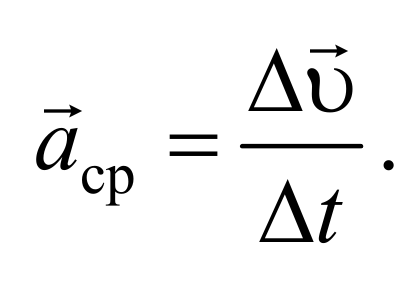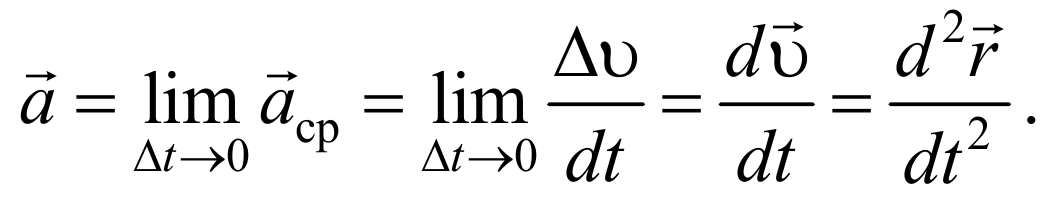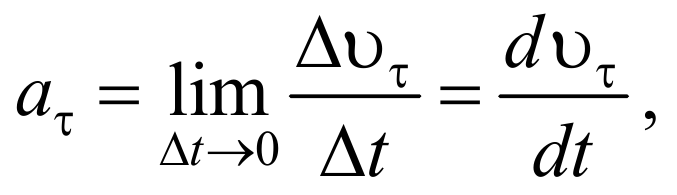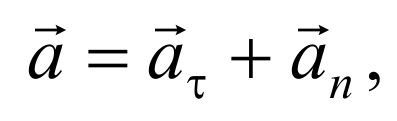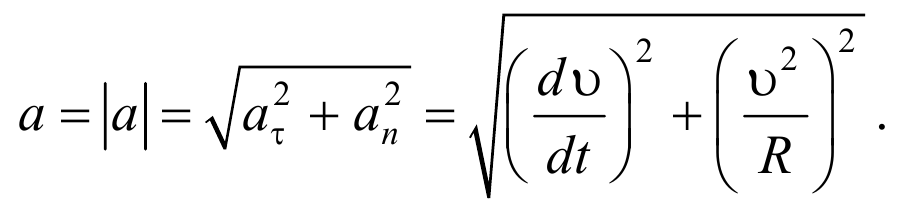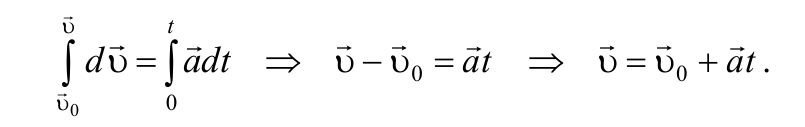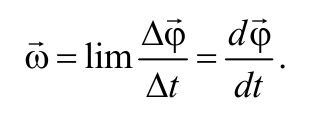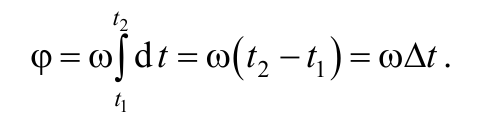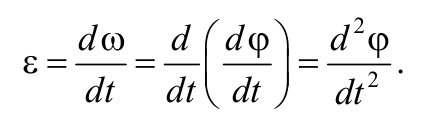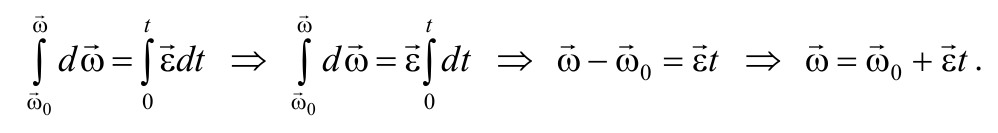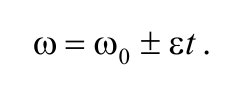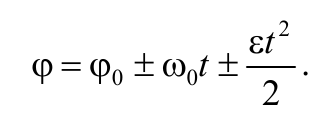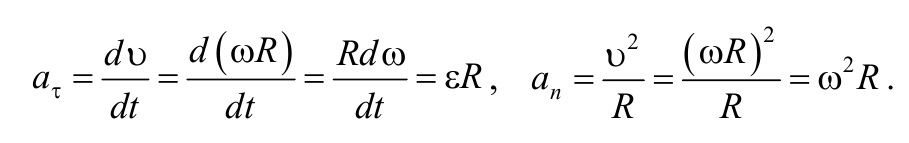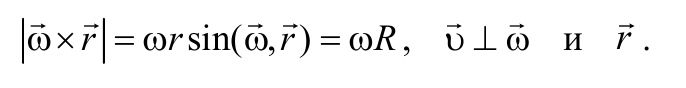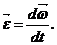связь угловых и линейных параметров вращающегося тела

Лекция №2. Элементы кинематики

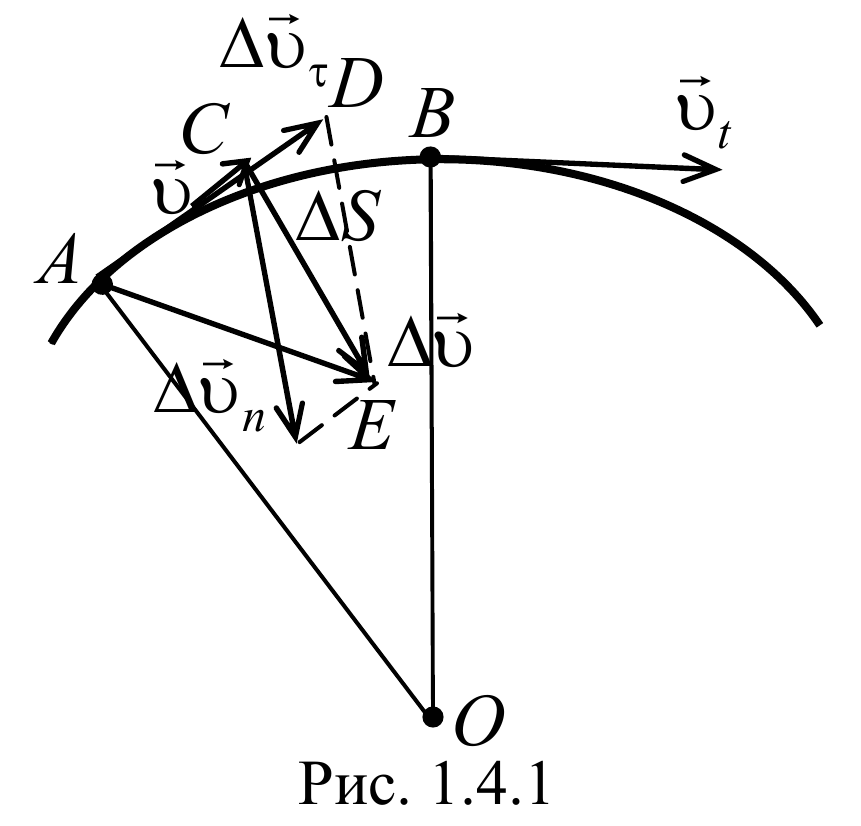
1.4. Нормальное и тангенциальное ускорения при криволинейном движении

В общем случае при движении тела его скорость изменяется как по величине, так и по направлению. Для характеристики быстроты изменения скорости движения вводится понятие ускорения.

Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.

Тангенциальная составляющая ускорения

т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны. Поэтому эту составляющую ускорения называют также центростремительным ускорением.

Таким образом, полное ускорение тела a есть геометрическая сумма тангенциальной a_τ и нормальной a_n составляющих

Тангенциальное ускорение равно первой производной по времени от модуля скорости и определяет быстроту изменения скорости по модулю, и направлено по касательной к траектории.

Нормальное ускорение определяет быстроту изменения скорости по направлению и направлено к центру кривизны траектории.

Векторы a_τ и a_n взаимно перпендикулярны поэтому модуль полного ускорения равен

1.5. Классификация движений материальной точки

В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:

3) a_τ= ƒ(t), a_n=0 − прямолинейное движение с переменным ускорением.

5) a_τ=const, a_n≠const − равнопеременное движение по окружности.

6) a_τ=0, a_n≠0 − равномерное криволинейное движение.

7) a_τ=const, a_n≠0 − криволинейное равнопеременное движение.

1.6. Кинематика абсолютно твердого тела

Угловой скоростью тела называется вектор, численно равный первой производной по времени от угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:

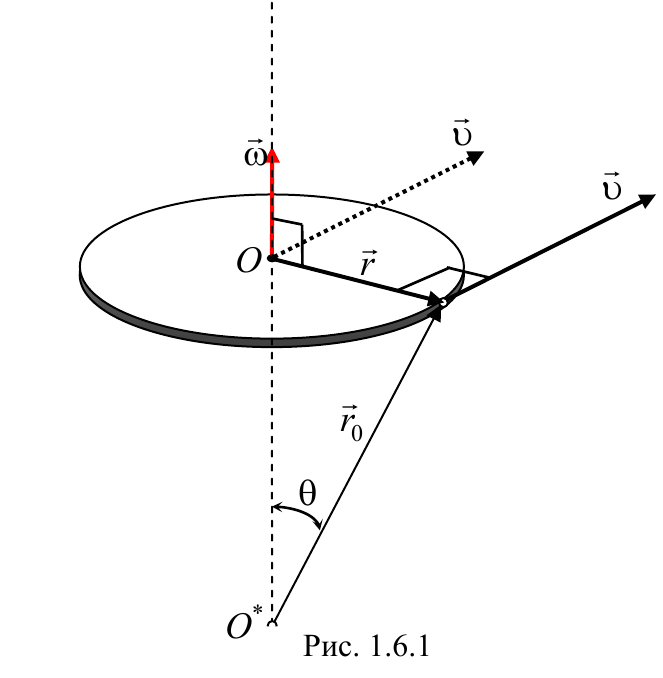
Вектор угловой скорости направлен по оси вращения, причем так, чтобы вращение, рассматриваемое с конца вектора угловой скорости, происходило против хода часовой стрелки (рис 1.6.1). Единицей угловой скорости является рад/с.

Скорость произвольной точки вращающегося тела называется линейной скоростью этой точки.

Равномерное вращение характеризуется периодом вращения и частотой вращения.

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

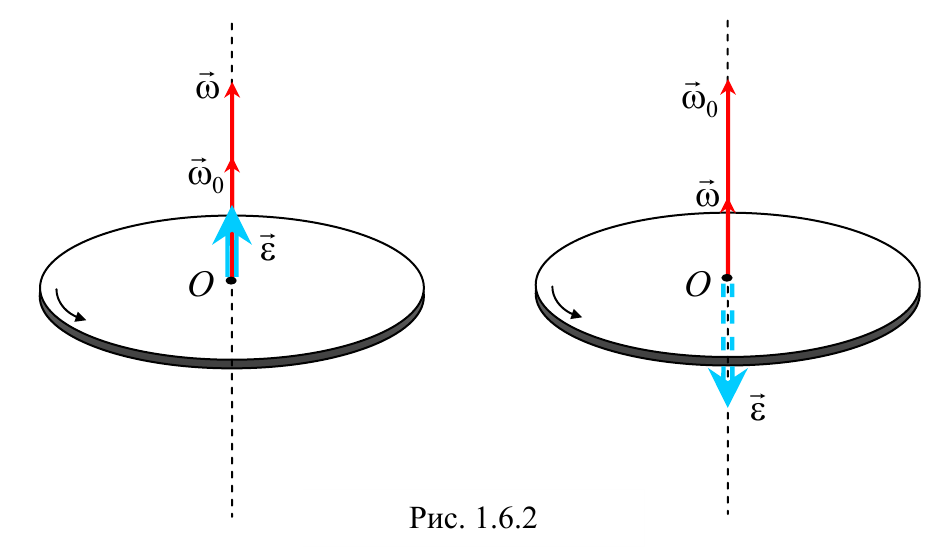
При ускоренном вращении вектор углового ускорения сонаправлен с вектором угловой скорости, а при замедленном − противоположен ему.

В случае равнопеременного движения точки по окружности (ε = const) угловая скорость определяется по формуле

Или в скалярном виде

Проинтегрировав выражение (1.6.1) можно получить формулу для угла поворота тела

1.7. Связь между линейными и угловыми характеристиками тела при его вращении

Тангенциальная и нормальная составляющие ускорения произвольной точки тела, вращающегося вокруг неподвижной оси, определяются формулами:

Источник

Учебники

Журнал «Квант»

Общие

Чивилёв В.И. Кинематика вращательного движения //Квант. — 1986. — № 11. — С. 17-18.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Содержание

Медленно проехав перекресток, троллейбус стал удаляться по улице, плавно увеличивая свою скорость.

Движение колеса троллейбуса — лишь один из многих примеров сложного механического движения в окружающем нас мире. Оказывается, любое сложное движение можно представить как сумму двух простых движений — поступательного и вращательного. Понимать это следует так: всегда можно подобрать такую поступательно движущуюся систему отсчета, относительно которой движение выглядит только как вращение вокруг некоторой неподвижной оси.

Какую же в нашем случае надо выбрать систему отсчета, чтобы в ней колесо троллейбуса совершало чистое вращение? Какими физическими величинами описывается это вращение, как эти величины связаны друг с другом и как зависят от времени? Такие вопросы могут возникнуть не только на пешеходном переходе, но и на уроке, экзамене, при решении конкретной задачи.

На первый вопрос ответить легко, догадавшись, что поступательно движущуюся систему отсчета можно связать с самим троллейбусом (его корпусом). Перед тем как ответить на остальные вопросы, заметим, что в нашем примере колесо вращается неравномерно — модуль скорости любой точки колеса меняется со временем.

Рассмотрим некоторую точку М колеса, находящуюся на расстоянии r от оси вращения и имеющую в некоторый момент времени скорость \(

\vec \upsilon\) и ускорение \(

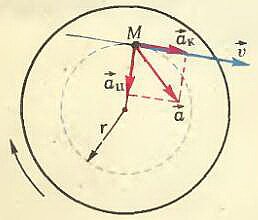
\vec a\) (рис. 1). Из физических соображений разумно ускорение \(

\vec a\) представить как сумму двух составляющих: одна из них \(

\vec a_c\) направлена по радиусу к центру окружности — центростремительное ускорение, вторая \(

\vec a_k\) направлена по касательной к окружности — касательное ускорение. Оба эти ускорения имеют определенный физический смысл — касательное ускорение характеризует быстроту изменения модуля скорости, а центростремительное характеризует быстроту изменения направления скорости. Можно показать, что модуль центростремительного ускорения \(

a_c = \frac<\upsilon^2>\) («Физика 8», §16), а модуль касательного ускорения \(

a_k = \frac<\Delta \upsilon><\Delta t>\), где Δυ — изменение модуля υ скорости точки за сколь угодно малое время Δt.

Линейные и угловые величины

Как уже говорилось, нам надо ввести такие физические величины, которые характеризовали бы неравномерное вращение колеса (в системе отсчета, связанной с троллейбусом). Попробуем это сделать по аналогии с прямолинейным неравномерным движением.

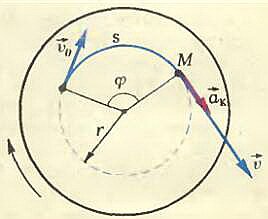
Проследим за точкой М колеса в течение малого промежутка времени Δt. За это время точка пройдет по дуге окружности путь s и будет иметь скорость υ и касательное ускорение a_k (рис. 2). Три величины s, υ и a_k, называемые линейными величинами, характеризуют движение точки М, но не могут служить для описания вращения всего колеса, так как в один и тот же момент времени другие точки, расположенные на других расстояниях от оси вращения, имеют другие линейные скорости, и касательные ускорения и пройденные ими пути тоже не одинаковы. Поэтому кроме линейных вводятся так называемые угловые величины, которые одинаковы для всех точек вращающегося колеса: угол поворота φ радиуса, соединяющего точку М с центром окружности, угловая скорость \(

\omega = \frac<\Delta \varphi><\Delta t>\) (Δφ — изменение угла поворота за время Δt) и угловое ускорение \(

\varepsilon = \frac<\Delta \omega><\Delta t>\) (Δω — изменение угловой скорости).

Очевидно, что введенными здесь угловыми величинами можно описывать вращение не только троллейбусного колеса, но и любого другого тела. При этом с течением времени может изменяться не только угол поворота φ, но и угловая скорость ω и угловое ускорение ε. В частности, если угловое ускорение не зависит от времени, то угловая скорость изменяется равномерно и в таком случае говорят, что имеет место равноускоренное вращение. Когда же угловая скорость остается постоянной, то угловое ускорение оказывается равным нулю и говорят о равномерном вращении тела.

Связь линейных и угловых величин

Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи.

При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь

За малое время Δt точка проходит расстояние \(

Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, но- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δt есть \(

Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.

Формулы кинематики для равноускоренного вращательного движения

Найдем зависимость угловой скорости ω и угла поворота φ колеса троллейбуса от времени t для случая вращения колеса с постоянным угловым ускорением ε.

Пусть начальная угловая скорость равна ω₀. Тогда точка М, имея начальную скорость υ₀ = rω₀, будет двигаться с постоянным по модулю касательным ускорением a_k = rε. По аналогии с прямолинейным равноускоренным движением для линейной скорости υ и пути s получим равенства

из которых после исключения времени t следует полезное соотношение:

Это и есть формулы кинематики для. вращательного движения любого тела (а не только колеса троллейбуса) с постоянным угловым ускорением.

Источник

Угловые характеристики движения и их связь с линейными.

Угловая скорость и угловое ускорение

Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис. 1.4).

Ее положение через промежуток времени t зададим углом .

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

Линейная скорость точки

Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения.

Таким образом,  = 2 n.

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости.

Тангенциальная составляющая ускорения

aτ = dv/dt = d(R)/dt =R d/dt = Rε

Нормальная составляющая ускорения

.

Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение аτнормальное ускорение аn) и угловыми величинами (угол поворота , угловая скорость , угловое ускорение ε) выражается следующими формулами:

В случае равнопеременного движения точки по окружности (ε =const)

Источник

Физика Б1.Б8.

Электронное учебное пособие по разделу курса физики Механика

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

Введение

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.

Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).

Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.

Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.

Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.

Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.

Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.

Источник

1.5. Связь между линейными и угловыми характеристиками движения вращающегося тела

Связь между линейным и угловым перемещениями уже найдена:

Разделим это выражение на dt:

.

Поскольку по определениюdr/dt=v, ad/dt=, полученное выражение связывает между собой линейную скорость точкиvс её угловой скоростью:

Таким образом линейная скорость точки тела, вращающегося с угловой скоростью  относительно неподвижной оси, равна векторному произведению угловой скорости тела на радиус-векторr, определяющий положение точки относительно оси вращения. Обратите внимание: линейная скорость разных точек твёрдого тела различна. Чем дальше от оси вращения расположена точка, тем выше её линейная скорость.

Возьмём производную от последнего выражения по времени:

Величина dv/dt по определению есть полное ускорение точкиa,d/dt — угловое ускорение,adr/dt — линейная скорость. Поэтому полученное выражение мы можем переписать в виде

Модуль полного ускорения

.

1.6. Преобразования галилея

Движение одного и того же тела можно наблюдать, находясь в разных системах отсчёта. Например, один наблюдатель может стоять на земле, а вто­рой равномерно и прямолинейно будет двигаться на автомобиле. Если каждый из наблюдателей измерит кинематические характеристики движения одного и того же тела, то результаты измерения будут разными. Очевидно, что если из­мерять скорость предмета, движущегося вместе с автомобилем, то у стоящего на земле наблюдателя измеренная скорость будет равна скорости автомобиля, а для сидящего в машине скорость предмета будет равна нулю. Но это скорости одного и того же тела, поэтому результаты измерений связаны между собой. Как именно они связаны, показывают преобразования Галилея.

Рассмотрим преобразования Галилея применительно к одной, простей­шей ситуации, а именно прямолинейному движению одной системы отсчёта относительно другой.

1) в момент t=t‘=0 начала координат систем отсчёта совпадали (t=t‘, так как Галилей полагал, что время во всех системах отсчёта течёт одинаково);

скорость v₀и ускорениеа₀начала координат движущейся системы отсчётаК’ относительно системы отсчётаК известны;

координаты, скорость и ускорение некоторой точки А относительно начала координат неподвижной системы отсчётаК известны.

Необходимо связать координаты, скорость и ускорение точки А в системах отсчётаКиК’.

Положение начала отсчёта движущейся системы относительно системы отсчёта Копределяется векторомr₀.

Положение точки А в системеК по условию определяется векторомr, положение точкиА в системеК векторомr‘. которые, как видно из рисунка, связаны соотношением

Пусть за время dt точкаА совершит в системе отсчётаК перемещениеdr. Перемещение точки в системеК равно сумме перемещенияdr₀ системыК’ относительно системы К и перемещенияdr‘ точкиАотносительно системыК’:

Если поделить выражение для перемещений на dt, то получим связь скоростей:

Взяв производную по времени от выражения для скоростей, получим связь ускорений:

Из последнего выражения видно, что если система отсчёта К  движется равномерно относительно системыК, т.е. еслиa_о=0, то ускорения точки в движущейся и неподвижной системах отсчёта одинаковыа=а‘.

Эти выражения и представляют собой преобразования Галилея. Если известны координаты, скорость и ускорение тела в какой-либо системе отсчёта и скорость другой системы отсчёта относительно данной системы, то преобразования Галилея позволяют вычислить значения всех кинематических характеристик рассматриваемого тела в другой системе отсчёта.

три независимые величины нужны в том случае, когда рассматривается движение в трёхмерном пространстве; в одномерном пространстве достаточно одной координаты

на рисунке бесконечно малое перемещение заменено на конечное

Термин «тело» будет использоваться вместо термина «абсолютно твёрдое тело».

Учтите, что это соотношение верно только для бесконечно малых поворотов d

Источник