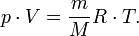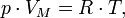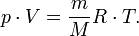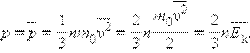температура является микроскопическим или макроскопическим параметром

Термодинамическая система. Микро- и макрохарактеристики системы. Макроскопическое состояние. Макроскопические параметры как средние значения. Температура.

Термодинамическая система,объект изучения термодинамики, совокупность физ. тел, которые могут взаимодействовать энергетически между собой и с другими телами, а также обмениваться с ними веществом. Т. с. состоят из столь большого числа частиц, что их состояние можно характеризовать макроскопическими параметрами: плотностью, давлением, концентрацией разных веществ, образующих её.

Микроскопическое состояние (или микросостояние) — это состояние системы, определяемое заданием координат и импульсов всех составляющих систему частиц.

Макроскопическое состояние (или макросостояние) — это состояние системы, характеризуемое небольшим числом величин (Р, V, T) и, быть может, еще некоторыми другими.

Величины, характеризующие макросостояние, называются макроскопическими характеристиками. Величины, характеризующие микросостояние, называются микроскопическими характеристиками.

Примерами макроскопических характеристик являются: давление, объем, температура и количество вещества.

Примерами микроскопических характериктик являются: количество частиц в веществе, температура одной частицы и т.д.

p = nkT

Основное уравнение молекулярно-кинетической теории для идеального газа устанавливает связь легко измеряемого макроскопического параметра — давления — с такими микроскопическими параметрами газа, как средняя кинетическая энергия и концентрация молекул.

Но, измерив только давление газа, мы не можем узнать ни среднее значение кинетической энергии молекул в отдельности, ни их концентрацию. Следовательно, для нахождения микроскопических параметров газа нужны измерения еще какой-то физической величины, связанной со средней кинетической энергией молекул. Такой величиной в физике является температура.

Абсолютная шкала температур. Шкала измерения температуры в соответствии с уравнением 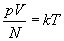называетсяабсолютной шкалой. Ее предложил английский физик У. Кельвин (Томсон) (1824—1907), поэтому шкалу называют также шкалой Кельвина.

До введения абсолютной шкалы температур в практике получила широкое распространение шкала измерения температуры по Цельсию. Поэтому единица температуры по абсолютной шкале, называемая кельвином (К), выбрана равной одному градусу по шкале Цельсия:

Абсолютный нуль температуры. В левой части уравнения 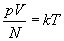все величины могут иметь только положительные значения или быть равными нулю. Поэтому абсолютная температура T может быть только положительной или равной нулю. Температура, при которой давление идеального газа при постоянном объеме должно быть равно нулю, называется абсолютным нулем температуры.

3. Тепловое равновесие. Равновесные состояния и процессы. Модель идеального газа. Уравнение состояния идеального газа (уравнения Клапейрона и Клапейрона – Менделеева). Изопроцессы.

В состоянии термодинамического равновесия:
— в системе прекращаются все необратимые процессы, связанные с изменением энергии: теплопроводность, диффузия, химические реакции и др.;
— макроскопические параметры системы не меняются со временем.

Равнове́сный тепловой процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близких равновесных термодинамических состояний.

Равновесный тепловой процесс называется обратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений.

Примеры равновесных процессов:

Изотермический процесс, при котором температура системы не изменяется (T=const)

Изохорный процесс, происходящий при постоянном объёме системы (V=const)

Изобарный процесс, происходящий при постоянном давлении в системе (P=const)

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Свойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:

§ объём частицы газа равен нулю (то есть, диаметр молекулы пренебрежимо мал по сравнению со средним расстоянием между ними, );

§ импульс передается только при соударениях (то есть, силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях);

§ суммарная энергия частиц газа постоянна (то есть, нет передачи энергии за счет передачи тепла или излучения)

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

Где — молярный объём,

Так как , где — количество вещества, а , уравнение состояния можно записать:

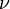
В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме

p = (γ − 1)ρε,

где — показатель адиабаты, — внутренняя энергия единицы массы вещества.

Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём илитемпература

— остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии —изоэнтропийный (например, обратимый адиабатический процесс).

Изобарный процесс (др.-греч. ισος, isos — «одинаковый» + βαρος, baros — «вес») — процесс изменения состояния термодинамической системы при постоянном давлении (P = const)

— Закон Гей-Люссака

‘Изохорный процесс (от греч. хора — занимаемое место) — процесс изменения состояния термодинамической системы при постоянном объёме (V = const). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объеме, давление прямо пропорционально температуре:

— закон Шарля (второй закон Гей-Люссака, 1808 г.)

Изотермический процесс (от греч. «термос» — тёплый, горячий) — процесс изменения состояния термодинамической системы при постоянной температуре (T = const).

При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.

— закон Бойля — Мариотта

Источник

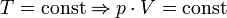
Термодинамическая система. Микро- и макрохарактеристики системы. Макроскопическое состояние. Макроскопические параметры как средние значения. Температура

Второе начало термодинамики

Второй закон термодинамики исключает возможность создания вечного двигателя второго рода.

1 — Постулат Клаузиуса. Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему

2 — Постулат Кельвина. Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара

Третье начало термодинамики может быть сформулировано так:

Приращение энтропии (как на меру беспорядка в системе) при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система.

Нулевое начало термодинамики (общее начало термодинамики)

— физический принцип, утверждающий, что вне зависимости от начального состояния изолированной системы в конце концов в ней установится термодинамическое равновесие, а также что все части системы при достижении термодинамического равновесия будут иметь одинаковую температуру. Тем самым нулевое начало фактически вводит и определяет понятие температуры. Нулевому началу можно придать чуть более строгую форму:

Если система A находится в термодинамическом равновесии с системой B, а та, в свою очередь, с системой C, то система A находится в равновесии с C. При этом их температуры равны.

Термодинамическая система,объект изучения термодинамики, совокупность физ. тел, которые могут взаимодействовать энергетически между собой и с другими телами, а также обмениваться с ними веществом. Т. с. состоят из столь большого числа частиц, что их состояние можно характеризовать макроскопическими параметрами: плотностью, давлением, концентрацией разных веществ, образующих её.

Микроскопическое состояние (или микросостояние) — это состояние системы, определяемое заданием координат и импульсов всех составляющих систему частиц.

Макроскопическое состояние (или макросостояние) — это состояние системы, характеризуемое небольшим числом величин (Р, V, T) и, быть может, еще некоторыми другими.

Величины, характеризующие макросостояние, называются макроскопическими характеристиками. Величины, характеризующие микросостояние, называются микроскопическими характеристиками.

Примерами макроскопических характеристик являются: давление, объем, температура и количество вещества.

Примерами микроскопических характериктик являются: количество частиц в веществе, температура одной частицы и т.д.

p = nkT

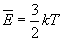
Основное уравнение молекулярно-кинетической теории для идеального газа устанавливает связь легко измеряемого макроскопического параметра — давления — с такими микроскопическими параметрами газа, как средняя кинетическая энергия и концентрация молекул.

Но, измерив только давление газа, мы не можем узнать ни среднее значение кинетической энергии молекул в отдельности, ни их концентрацию. Следовательно, для нахождения микроскопических параметров газа нужны измерения еще какой-то физической величины, связанной со средней кинетической энергией молекул. Такой величиной в физике является температура.

Абсолютная шкала температур. Шкала измерения температуры в соответствии с уравнением 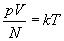называетсяабсолютной шкалой. Ее предложил английский физик У. Кельвин (Томсон) (1824—1907), поэтому шкалу называют также шкалой Кельвина.

До введения абсолютной шкалы температур в практике получила широкое распространение шкала измерения температуры по Цельсию. Поэтому единица температуры по абсолютной шкале, называемая кельвином (К), выбрана равной одному градусу по шкале Цельсия:

Абсолютный нуль температуры. В левой части уравнения 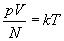все величины могут иметь только положительные значения или быть равными нулю. Поэтому абсолютная температура T может быть только положительной или равной нулю. Температура, при которой давление идеального газа при постоянном объеме должно быть равно нулю, называется абсолютным нулем температуры.

3. Тепловое равновесие. Равновесные состояния и процессы. Модель идеального газа. Уравнение состояния идеального газа (уравнения Клапейрона и Клапейрона – Менделеева). Изопроцессы.

В состоянии термодинамического равновесия:
— в системе прекращаются все необратимые процессы, связанные с изменением энергии: теплопроводность, диффузия, химические реакции и др.;
— макроскопические параметры системы не меняются со временем.

Равнове́сный тепловой процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близких равновесных термодинамических состояний.

Равновесный тепловой процесс называется обратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений.

Примеры равновесных процессов:

Изотермический процесс, при котором температура системы не изменяется (T=const)

Изохорный процесс, происходящий при постоянном объёме системы (V=const)

Изобарный процесс, происходящий при постоянном давлении в системе (P=const)

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Свойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:

§ объём частицы газа равен нулю (то есть, диаметр молекулы 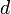пренебрежимо мал по сравнению со средним расстоянием между ними, );

§ импульс передается только при соударениях (то есть, силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях);

§ суммарная энергия частиц газа постоянна (то есть, нет передачи энергии за счет передачи тепла или излучения)

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

Где 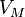— молярный объём,

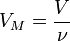
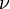
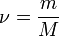
Так как , где — количество вещества, а , уравнение состояния можно записать:

В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме

p = (γ − 1)ρε,

где — показатель адиабаты, — внутренняя энергия единицы массы вещества.

Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём илитемпература — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии —изоэнтропийный (например, обратимый адиабатический процесс).

Изобарный процесс (др.-греч. ισος, isos — «одинаковый» + βαρος, baros — «вес») — процесс изменения состояния термодинамической системы при постоянном давлении (P = const)

— Закон Гей-Люссака

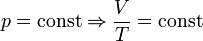
‘Изохорный процесс (от греч. хора — занимаемое место) — процесс изменения состояния термодинамической системы при постоянном объёме (V = const). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объеме, давление прямо пропорционально температуре:

— закон Шарля (второй закон Гей-Люссака, 1808 г.)

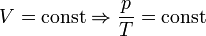
Изотермический процесс (от греч. «термос» — тёплый, горячий) — процесс изменения состояния термодинамической системы при постоянной температуре (T = const).

При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.

— закон Бойля — Мариотта

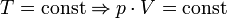
4. Основное уравнение МКТ идеального газа для давления. Следствия из основного уравнения. Молекулярно – кинетическое толкование абсолютной температуры.

Формула для среднего давления газа на стенку сосуда записывается в виде

Это уравнение устанавливает связь между давлением p идеального газа, массой молекулы m₀, концентрацией молекул n, средним значением квадрата скорости и средней кинетической энергией поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.

— следствие из МКТ идеального газа

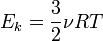
Температура – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. В соответствии с решением XI Генеральной конференции по мерам и весам (1960г.) в настоящее время рекомендовано применять только две температурные шкалы – термодинамическую и Международную практическую, градуированные соответственно в кельвинах и градусах Цельсия. Анализ показывает, что 0К (абсолютный нуль) недостижим, хотя приближение к нему сколь угодно близко возможно.

Любое изменение в термодинамической системе, связанное с изменением хотя бы одного его термодинамического параметра, называется термодинамическим процессом. Макроскопическая система находится в термодинамическом равновесии, если её состояние с течением времени не меняется (предполагается, что внешние условия рассматриваемой системы при этом не изменяются).

Абсолютная температура – Т(k) = t°(c) + 273°

С точки зрения молекулярно-кинетической теории абсолютная температура есть величина, пропорциональная средней энергии поступательного движения молекулы. =3/2kT.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Макроскопические параметры

Любое макроскопическое тело или группа макроскопических тел называется термодинамической системой (от греч. systema — целое, составленное из частей).

Величины, характеризующие состояние термодинамической системы без учета молекулярного строения тел, называют макроскопическими (или термодинамическими) параметрами. Макроскопические параметры не исчерпываются объемом, давлением и температурой. Например, для смеси газов нужно знать концентрации отдельных компонентов смеси. Если вещество находится в электрическом или магнитном поле, то необходимо задать характеристики этих полей в веществе.

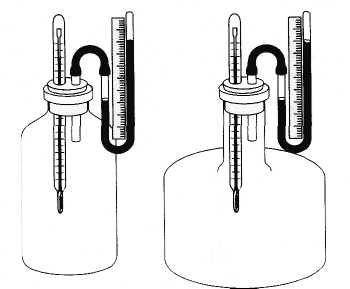
В то же время форма сосуда, в котором находится газ, не является существенной для определения его состояния. Например, кислород в сосуде, изображенном на рисунке 3.1, а, будет находиться точно в таком же состоянии, в каком и кислород в сосуде другой формы (рис. 3.1, б), если объемы сосудов, массы и температуры газов одинаковы. В частности, давления газов в обоих сосудах равны. Не зависит от формы сосуда сжимаемость газа и его другие свойства.

Давление газа в молекулярно-кинетической теории

На примере давления газа выясним, какой смысл имеют макроскопические параметры с молекулярно-кинетической точки зрения.

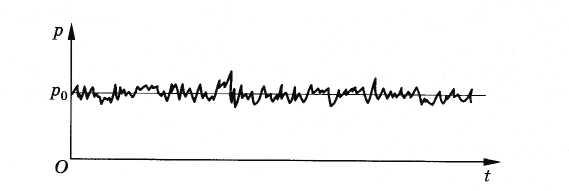
Пусть газ находится в закрытом сосуде. Манометр показывает давление газа р₀. Как возникает это давление? Каждая молекула газа, ударяясь о стенку, в течение малого промежутка времени действует на нее с определенной силой. В результате беспорядочных ударов о стенку сила, действующая со стороны всех молекул на поверхность стенки единичной площади, т. е. давление, будет быстро меняться со временем примерно так, как показано на рисунке 3.2. Однако действия, вызванные ударами отдельных молекул, настолько слабы, что манометром они не регистрируются. Манометр фиксирует среднюю по времени силу, действующую на каждую единицу площади поверхности его чувствительного элемента — мембраны. Несмотря на небольшие изменения давления, среднее значение давления р₀ практически оказывается вполне определенным, так как ударов о стенку очень много, а массы молекул очень малы.

Состояние термодинамической системы характеризуется макроскопическими параметрами — объемом, давлением и температурой.

§ 3.2. Температура. Тепловое равновесие

Термометрами пользуются все. А что они измеряют? Конечно, температуру! Однако это еще не ответ. Что означают слова: «Я измерил температуру тела»? Что я при этом узнал? Что именно характеризует температура? Это не так просто, как может показаться на первый взгляд.

Субъективные представления о температуре

В геометрии вводят одну основную величину — длину. Остальные величины: площадь и объем — производные. В кинематике добавляют еще одну величину — время. Скорость, ускорение являются производными. В динамике еще одной основной величиной становится масса. В теории тепловых явлений единственная новая основная величина, которую надо ввести, — это температура.

В коже нашего тела, кроме чувствительных приемников, реагирующих на прикосновение, давление и болевые раздражения, есть приемники, реагирующие на раздражение ощущением тепла и холода. Руководствуясь этим, можно все тела расположить в ряд по их способности вызывать ощущения тепла и холода. Причину способности тел по-разному воздействовать на органы чувств можно связать с различной степенью нагретости тел — температурой. Это только качественное, субъективное определение температуры, не содержащее указаний на способ ее измерения. В отличие от измерения длины, времени, массы и т. д. прошло длительное время, прежде чем на смену субъективным впечатлениям о температуре пришли точные и единые методы ее измерения. Развитие методов измерения температуры стало возможным лишь тогда, когда была установлена зависимость от температуры таких величин, как длина, объем и т. д., которые можно измерять непосредственно.

Источник