термодинамические параметры влажного воздуха
Лекция Термодинамические свойства влажного воздуха



Санкт-Петербург
ТЕРМОДИНАМИКА
(КОНСПЕКТ ЛЕКЦИЙ)
Воздух, движущийся по горным выработкам, заполняющий трещины и пустоты в горном массиве, является одной из термодинамических систем, определяющих динамику тепловых процессов при освоении ресурсов недр. Состоящий из кислорода, азота, углекислого газа, небольшого количества инертных примесей, воздух всегда содержит некоторое количество водяного пара. Эта смесь сухого воздуха с водяным паром называется влажным воздухом.
К основным термодинамическим параметрам влажного воздуха относятся влажность j, парциальное давление насыщенного пара – rпн, влагосодержание – d, плотность – r, теплосодержание – i.
С достаточной для технических расчетов точностью можно считать, что влажный воздух подчиняется всем законам смеси идеальных газов. Каждый газ, в том числе и пар, входящий в состав смеси, занимает тот же объем V, что и вся смесь. Он имеет температуру смеси Т, находится под своим парциальным давлением рi, которое определяют по уравнению Клайперона :
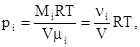
где – 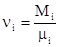
Mi – масса i-того газа, кг;
mi – молекулярный вес газа, кг/моль;
R – универсальная газовая постоянная, равная 8,314 кДж/кмоль×К.
Отношение массы газа (Мi) к объему смеси V называется концентрацией (wi) данного газа в смеси.
Сумма парциальных давлений газовых компонентов смеси равна полному давлению смеси (закон Дальтона):
Влажный воздух можно, в первом приближении, рассматривать как бинарную смесь, состоящую из водяного пара и приведенного однородного газа – сухой части атмосферного воздуха, эффективный молекулярный вес которого mв = 29. Тогда барометрическое давление влажного воздуха рб будет равно сумме парциальных давлений сухого воздуха pв и водяного пара рп, т.е.
Смесь, которая состоит из сухого воздуха и перегретого водяного пара, называют ненасыщенным влажным воздухом, а смесь, состоящую из сухого воздуха и насыщенного водяного пара, – насыщенным влажным воздухом.
Относительная влажность воздушно-паровой смеси представляет собой отношение концентрации водяного пара ненасыщенного воздуха к концентрации водяного пара насыщенного воздуха при одинаковых температурах и давлениях:
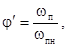
где wп – концентрация водяного пара ненасыщенного воздуха, кг/м 3 ;
Из выражения (1.4) следует, что относительная влажность насыщенного влажного воздуха равна единице.
Относительную влажность воздуха можно также выразить отношением парциальных давлений водяного пара. Для этой цели воспользуемся уравнением Клайперона (1.1):

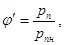
где рн и рпн – соответственно парциальное давление ненасыщенного пара и давления насыщенного пара при температуре воздушно-паровой смеси (Па).
Давление насыщенного водяного пара является функцией только температуры. Оно может быть найдено по таблицам или, с известным приближением, по формуле:
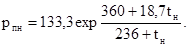
Величину относительной влажности воздуха часто выражают в процентах, j = j¢×100% = wп/wпн×100%.
Влагосодержание влажного воздуха d есть отношение массы пара к единице массы сухого воздуха, содержащегося в смеси, т.е.
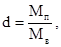
где Мп и Мв – соответственно масса пара и масса сухого воздуха (г, кг).
Из уравнения Клайперона для пара и воздуха с учетом знаний молекулярного веса пара mп = 18 молекулярного веса воздуха mв = 29 можно получить выражение для определения влагосодержания (кг/кг сух. возд.)
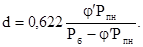
Влагосодержание воздуха пропорционально барометрическому давлению и является функцией только парциального давления пара.
Величина барометрического давления атмосферного воздуха на уровне моря в среднем составляет 760 мм. рт.ст. (101,3×10 3 Па) и колеблется в пределах от 720 до 800 мм рт.ст. (от 96×10 3 до 106,8×10 3 Па).
С изменением высоты над уровнем моря барометрическое давление изменяется и его можно вычислить с достаточной точностью по формуле:
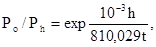
где h– высота над уровнем моря. м; t – средняя температура воздуха на участке между уровнем моря и рассматриваемой точкой; Ро – давление над уровнем моря, в среднем, равное 760 мм рт.ст. (101,3 10 3 Па); Рh— искомое давление на высоте h.
Повышение барометрического давления с увеличением глубины Н можно определить по формуле
где rв – плотность столба воздуха высотой Н при средней температуре t, кг/м 3 ; g – ускорение свободного падения, м 2 /с.
Плотность влажного воздуха представляет собой отношение массы воздушно-паровой смеси М к объему этой смеси V:
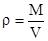
Выразив отношение Mn через концентрации сухого воздуха wв и водяного пара wп, а последние через влагосодержание, получим:
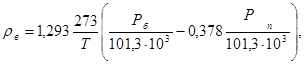
где Рп – парциальное давление пара находится из формул (1.5), (1.6).
Из этого выражения видно, что влажный воздух всегда легче сухого, т.к. молекулярный вес пара меньше молекулярного веса воздуха. Таким образом, чем больше величина Рп, тем легче будет воздушно-паровая смесь. Однако это будет справедливо только в том случае, когда молекулярный вес паров меньше молекулярного веса воздуха. Если молекулярный вес пара какого-либо вещества (например, паров бензола) будет больше молекулярного веса воздуха, то картина наблюдается обратная (подобные случаи встречаются в практике промышленной вентиляции).
Влияние температуры на плотность смеси в обоих случаях будет одинаковым: с повышением температуры плотность смеси начнет уменьшаться, и наоборот.
Удельную теплоемкость влажного воздуха ссм (Дж/кг сух. возд. ×К) относят, как и влагосодержание, к единице массы сухой части воздуха:
где св – средняя удельная теплоемкость сухого воздуха (для температур в интервале 0-100°С св принимают равной 1,005 кДж/кг×К); сп – средняя удельная теплоемкость водяного пара (равная 1,8 кДж/кг×К).
Удельное теплосодержание сухого воздуха (энтальпия) (кДж/кг) равна:
Удельное теплосодержание насыщенного пара (энтальпия) (Дж/кг) определяется выражением
где iж – теплосодержание жидкости, кДж/кг; сж – теплоемкость жидкости, кДж/кг; r – удельная теплота испарения, кДж/кг; tж – температура жидкости, °С.
Величина r зависит от температуры жидкости, и ее можно определить по следующей эмпирической формуле, предложенной Н.И.Фильнеем:
Энтальпия насыщенного пара равна:
Удельное теплосодержание перегретого пара (энтальпия) iп.п (кДж/кг), содержащегося во влажном воздухе при температуре t, составляет:
iп.п = 2500 + 1,8068×t (1.19)
Таким образом, теплосодержание как перегретого, так и насыщенного пара равно сумме теплосодержания его при 0°С и теплоты перегрева от 0 до t градусов.
Теплосодержание влажного воздуха (энтальпия) (кДж/кг сух. возд.) обычно относят к единице веса сухого пара, т.е. к 1 кг его:
i = 1,005t + (2500 + 1,8068t) ×d (1.20)
Л.К.Рамзин, используя выражение (1.20), построил i-d диаграмму, которая широко применяется в расчетах сушки, кондиционирования воздуха и в ряде других расчетов, связанных с изменением состояния влажного воздуха. Эта диаграмма выражает графическую зависимость основных параметров воздуха (t, j, рп, d и t) при заданном барометрическом давлении).
I-D диаграмма (рис. 1.1) построена в косоугольной системе координат с углом между осями (i и d) a = 135°. На вспомогательной оси 0d1 в масштабе с интервалом, соответствующим 1 г, откладываются величины влагосодержаний d и через полученные таким образом точки проводятся вертикальные линии постоянного влагосодержания (d = const).
По оси ординат откладывают величины теплосодержаний i с интервалом 1 см – 2 кДж/кг сух. возд.
С помощью i-d диаграммы на основании известных любых двух параметров воздуха можно найти и остальные его параметры.
ОСНОВЫ ТЕРМОДИНАМИКИ ВЛАЖНОГО ВОЗДУХА
6.1. Термодинамические свойства влажного воздуха
Сухой воздух состоит из азота, кислорода и небольшого количества двуокиси углерода и инертных газов (аргона, гелия, неона и др.). Основные составляющие воздуха –– азот и кислород, поэтому в практических расчётах принимают, что сухой воздух состоит по объему из 21% кислорода и 79% атмосферного азота (под последним подразумевается совокупность всех газов, входящих в воздух, кроме кислорода).
Атмосферный воздух, используемый в теплотехнике, содержит то или иное количество водяного пара. Смесь сухого воздуха с водяным паром называется влажным воздухом. Знание термодинамических свойств влажного воздуха необходимо для расчётов систем вентиляции и кондиционирования воздуха и процессов сушки влажных материалов.
В указанных процессах полное давление воздуха близко к атмосферному, а парциальное давление водяного пара невелико, поэтому влажный воздух можно считать смесью идеальных газов. Однако этот частный случай газовой смеси приходится изучать особо, так как в важном для практике интервале температур от –50 до +100ºС сухой воздух находится только в газообразном состоянии, а Н2О может находиться в виде паровой, жидкой либо твердой фазы в зависимости от температуры и полного давления смеси. Поэтому количество водяного пара во влажном воздухе при данной температуре не может превышать определённого значения. В этом состоит отличие влажного воздуха от обычных газовых смесей.
Согласно закону Дальтона для смесей идеальных газов полное давление влажного воздуха р равно сумме парциальных давлений сухого воздуха рв и водяного пара рп:
Состоянию влажного воздуха, заданному полным давлением, температурой и относительной влажностью, соответствуют два предельных состояния с максимально-возможным содержанием водяного пара. Влажный воздух в таких состояниях называется насыщенным и состоит из сухого воздуха и насыщенного пара. В насыщенном воздухе парциальное давление водяного пара рправно давлению насыщения рs при заданной температуре, то есть рп = рs.
Если рп 3 влажного воздуха и выраженную в граммах. Она примерно равна парциальному давлению водяного пара в мм ртутного столба.
Относительной влажностью воздуха φ называется отношение массы пара, содержащейся в 1 м 3 влажного воздуха ρп, к массе пара в 1 м 3 насыщенного воздуха ρн при одинаковых значениях полного давления и температуры воздуха
 | (6.2) |
Поскольку плотности ρп и ρs определяются при одной и той же температуре, то для идеального газа их отношение можно заменить отношением давлений
 | (6.3) |
Для насыщенного воздуха φ = 1 (φ = 100%), а для ненасыщенного φ
 | (6.4) |
Величину d обычно измеряют в килограммах влаги на килограмм сухого воздуха, но на диаграмме H, d (см. п. 6.2) значения d приведены в граммах на килограмм.
Иногда рассчитывают мольное влагосодержание x – отношение числа молей водяного пара к числу молей сухого воздуха в данном объёме
 | (6.5) |
Величины d и x характеризуют влажный воздух, в котором вода может находиться как в виде пара, так и в виде капель влаги либо кристаллов льда.
Если считать компоненты влажного воздуха идеальными газами, то уравнения состояния для пара и сухого воздуха при общих Т и V запишутся так:
  | (6.6) |
Разделив почленно первое уравнение на второе и выразив массовое влагосодержание Мп/Мв в килограммах влаги на килограмм сухого воздуха, получим окончательно
 , , | (6.7) |
где р – полное давление влажного воздуха.
Соотношение (6.7) справедливо, если влага содержится в воздухе в виде пара, так как только в этом случае можно применять уравнение состояния идеального газа (6.6). Поэтому величину dп правильнее называть паросодержанием. Для насыщенного воздуха уравнение (6.7) принимает вид
 , , | (6.8) |
где ds –– максимальное паросодержание воздуха, кг/кг.
Влажный воздух характеризует также отношение
 | (6.9) |
называемое степенью насыщения. С учетом формул (6.7) и (6.8) получаем
 | (6.10) |
Если температура влажного воздуха не слишком велика, то рs и рп малы по сравнению с полным давлением влажного воздуха р, и тогда ψ ≈φ.
Для расчета плотности влажного воздуха как смеси двух газов запишем выражение для его газовой постоянной
 , , | (6.11) |
где xв и xп –– мольные доли сухого воздуха и водяного пара.
Мольную долю каждого из компонентов можно выразить как отношение его парциального давления к давлению смеси
  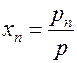 . . | (6.12) |
Тогда выражение для Rсм можно записать в виде
 | (6.13) |
Преобразовав знаменатель дроби, получим
 | (6.14) |
Зная Rсм, запишем уравнение состояния влажного воздуха
 | (6.15) |
 | (6.16) |
Из (6.16) следует, что чем больше влажность воздуха (чем выше значение рп), тем меньше его плотность. Таким образом, влажный воздух всегда легче сухого.
Энтальпия влажного воздуха является аддитивной величиной и определяется как сумма энтальпий сухого воздуха и водяного пара, имеющих общую точку отсчёта. Эту величину относят к 1 кг сухого воздуха
 . . | (6.17) |
Энтальпию сухого воздуха определяют в идеально-газовом приближении по формуле hв = cp0·t = 1,0048t, кДж/кг. Энтальпию водяного пара находят по таблицам его свойств либо по формуле hп = 2501 + 1,93t, кДж/кг, где 2501 –– теплота парообразования воды при 0ºС, а слагаемое 1,93t –– теплота перегрева пара от 0ºС до tºC.
Подставляя значения энтальпии сухого воздуха и водяного пара в уравнение (6.17), получаем
Если влажный воздух насыщенный, то в формулу (6.18) вместо dп надо подставлять ds.
В общем случае влажный воздух может содержать влагу не только в виде пара, но и в виде жидкости либо льда. Тогда выражение для энтальпии влажного воздуха имеет вид
где hж и hт –– значения энтальпии воды и льда.
Подставив в (6.19) выражения для hж и hт, получим
| Н = 1,0048t + (2501+1,93t)ds + 4,19tdж + + (–335 + 2,1t)dт, | (6.20) |
где коэффициенты 4,19 и 2,1 –– теплоёмкости воды и льда, а число 335 –– теплота плавления льда.
В том случае, когда в воздухе содержатся вода либо лёд, паросодержание является максимально возможным при данной температуре (dп = ds).
Массовую теплоёмкость влажного воздуха рассчитывают по формуле, аналогичной формуле (6.17):
 . . | (6.21) |
Для определения относительной влажности воздуха часто применяют психрометр, состоящий из двух термометров –– сухого и так называемого мокрого. Сухой термометр показывает температуру воздуха tс, мокрый –– температуру воды, содержащейся во влажной ткани. Ею обмотан шарик этого термометра с находящимся в нём веществом (ртутью либо спиртом). Вода испаряется с поверхности ткани тем интенсивнее, чем меньше относительная влажность воздуха.
На испарение воды затрачивается теплота парообразования, поэтому температура воды и влажной ткани понижается. В пределе она могла бы понизиться до точки росы tр, но ввиду притока теплоты к ткани от близлежащих слоёв воздуха тепловое равновесие устанавливается не при tр, а при более высокой температуре, называемой температурой мокрого термометра tм. Чем суше воздух, тем больше разность значений tси tм. Если же воздух насыщен водяным паром (φ = 100%), то показания обоих термометров совпадают.
Зависимость паросодержания воздуха dп от величин tси tм устанавливают опытным путём. По результатам опытов составляют специальные психрометрические таблицы либо диаграммы, с помощью которых можно по показаниям психрометра определить значения dп и φ. В психометрических таблицах приводятся также данные о парциальном давлении пара, плотности, теплоёмкости и энтальпии влажного воздуха в зависимости от температуры и относительной влажности.
6.2 Диаграмма H,d влажного воздуха
Приведенные выше соотношения можно использовать для расчёта и исследования термодинамических процессов, протекающих во влажном воздухе. Однако для инженерных расчетов и анализа процессов тепло- и массообмена во влажном воздухе более широко применяют диаграмму H,d. Нанесенные на эту диаграмму значения H в зависимости от d для различных температур рассчитаны по уравнению (6.18).
Рассмотрим изотермы ненасыщенного влажного воздуха в координатах H,d. Дифференцируя уравнение (6.18) по dп при t = const, получим
 | (6.22) |
Отсюда следует, что изотермы ненасыщенного воздуха в указанных координатах являются прямыми линиями, угол наклона которых увеличивается с ростом температуры.
Предельная точка на изотерме, соответствующая максимальному паросодержанию ds, находится на линии насыщения (φ = 100%). Величина ds рассчитывается из соотношения (6.8) по известным значениям атмосферного давления р и давления насыщения водяного пара рs; она различна для разных изотерм. Чем выше температура, тем больше величина ds, поэтому на диаграмме Н,d линия насыщения имеет положительный наклон. Диаграмма Н,d строится обычно для значения атмосферного давления р = 0,1 МПа. С ростом давления значение ds на каждой изотерме уменьшается и линия насыщения в координатах H,d смещается влево и вверх. В то же время каждая изотерма ненасыщенного воздуха остается общей для различных значений полного давления влажного воздуха (пока справедливо идеально-газовое приближение).
В прямоугольной системе координат изотермы ненасыщенного воздуха занимают узкую полосу на диаграмме H,d, так как энтальпия влажного воздуха сильно меняется с изменением dп, но сравнительно мало –– с изменением температуры. Поэтому гораздо более удобна косоугольная диаграмма H,d с углом примерно 135º между осями. В этом случае можно увеличить масштаб по оси энтальпии и важная для расчётов область ненасыщенного воздуха занимает значительно бὀльшую площадь, чем на прямоугольной диаграмме. Линии постоянного влагосодержания (d = const) в косоугольной диаграмме располагаются вертикально, параллельно оси ординат, а изоэнтальпы (H = const) –– под углом примерно 135º к этой оси. Наклон изотерм в косоугольной системе координат увеличивается с ростом температуры (при t > 0ºC).
| Рис 6.1 Диаграмма Н,d влажного воздуха |

При добавление пара в насыщенный влажный воздух пар будет конденсироваться на абсорбирующей поверхности, либо будет образовываться туман. Область тумана на диаграмме H,d располагается ниже и правее линии насыщения. Дифференцируя выражение (6.20) по d при t = const с учетом условий dп = ds = const и dт = 0, можно установить что изотермы в области тумана –– прямые линии с углом наклона, равным 4.19t. При переходе через линию насыщения изотерма претерпевает излом, и её наклон в области тумана значительно меньше, чем в области ненасыщенного воздуха. Поскольку область тумана является метастабильной и не представляет интереса при расчёте систем кондиционирования воздуха, изотермы в ней не строят, а проводят там линию парциального давления водяного пара как функцию паросодержания.
Точку на диаграмме H,d, характеризующую состояние влажного воздуха, задают значениями двух параметров, не связанных однозначной зависимостью друг с другом, например, значениями d и H, d и t, d и φ, t и φ. После нахождения этой точки можно определить остальные параметры влажного воздуха в заданном состоянии. В частности, значение температуры росы tр определяют, проводя из данной точки прямую линию d = const до пересечения с кривой насыщенного влажного воздуха. Аналогичным образом определяют температуру мокрого термометра tм, проводя линию Н = соnst.
6.3. Изображение основных процессов изменения состояния влажного воздуха на диаграмме H,d
Процессы тепло- и массообмена во влажном воздухе изображаются на диаграмме H,d непрерывными линиями. Если каждый последующий микропроцесс во влажном воздухе совершается подобно предыдущему, то макропроцесс, образованный их совокупностью, изображается на этой диаграмме прямой линией. Направление процесса характеризуется уклоном процесса, который рассчитывается по формуле
 | (6.23) |
то есть является отношением теплоты изобарного процесса ΔH к соответствующему изменению влагосодержания Δd. Величину ε часто называют тепловлажностным отношением; она может изменяться от –∞ до +∞.
Характеристикой процесса является также коэффициент влаговыпадения ξ, который определяется как отношение полной теплоты процесса к ощутимой теплоте срʹΔt, идущей на изменение температуры влажного воздуха
 | (6.24) |
Расчёты процессов тепло- и массообмена во влажном воздухе можно проводить как аналитически, так и графически (с помощью диаграммы Н, d). Аналитические методы более точны, графические –– нагляднее и проще. Поэтому аналитические методы применяют при оптимизационных расчётах процессов на ЭВМ, а графические –– при ориентировочных расчётах и качественном анализе процессов обработки и использования влажного воздуха.
При графическом решении задач значение изобарной теплоёмкости влажного воздуха принимают постоянным и равным 1 кДж/(кг.К). При аналитическом решении целесообразно рассчитывать значение срʹ по формуле (6.21).
В технике кондиционирования воздуха часто смешиваются несколько потоков воздуха, отличающихся по состоянию и массе. Рассмотрим процесс смешения двух потоков, состояние которых характеризуется на диаграмме Н,d точками 1 и 2 (рис. 6.2). Воздух с параметрами t1 и φ1 имеет массу М1 кг, а воздух с параметрами t2 и φ2 –– массу М2. Точка С, соответствующая состоянию смеси этих потоков, может быть найдена из уравнений баланса теплоты и влаги:
Из этих уравнений можно найти энтальпию и влагосодержание смеси:
 , , | (6.27) |
 . . | (6.28) |
По найденным параметрам с помощью диаграммы Н,d можно легко определить остальные параметры смеси.
Решая совместно уравнения (6.25) и (6.26), получим:
 | (6.29) |
| Рис 6.2. Определение параметров смеси потоков воздуха на диаграмме H,d. |

Рассмотрим на диаграмме Н,d процесс охлаждения влажного воздуха. При этом возможны два случая: когда температура охлаждающей поверхности выше точки росы tpлибо равна ей и когда температура этой поверхности ниже tp.
В первом случае охлаждение влажного воздуха от температуры t1 до t2 протекает по линии d = const и не сопровождается конденсацией влаги на поверхности охлаждения (рис.6.3а). Относительная влажность воздуха в данном процессе увеличивается от φ1 до φ2. Такой процесс называется сухим охлаждением воздуха. В пределе он заканчивается на кривой насыщенного влажного воздуха φ = 100%.
| Рис 6.3. Изображение процессов охлаждения и нагрева воздуха на диаграмме Н,d. |

На диаграмме Н,d данный процесс условно изображается прямой 1–2. Состояние воздуха на выходе из охладителя должно изображаться точкой С на этой прямой. Чем больше поверхность охлаждения, тем ближе точка С к точке 2.
Процесс 1–2 называется «мокрым охлаждением». При этом уменьшается влагосодержание воздуха, но повышается его относительная влажность. Если задано состояние воздуха на входе в охладитель (точка 1), то область мокрого охлаждения на диаграмме H,d ограничивается прямой 1–Р, характеризующей предельный процесс при сухом охлаждении, и прямой 1–К, касательной к линии насыщения.
При нагреве влажного воздуха в поверхностном подогревателе его влагосодержание не изменяется, температура растёт, а относительная влажность уменьшается. На диаграмме H,d изменение состояния воздуха при этом изображается прямой d = const (рис. 6.3в); точка 1 соответствует начальному, а точка 2 –– конечному состоянию воздуха. Положение точки 2 на диаграмме можно определить по температуре воздуха на выходе из подогревателя.
При тепловлажностной обработке влажного воздуха наблюдается так называемая недорекуперация, когда температура либо влагосодержание воздуха отличаются от соответствующих параметров поверхности (среды), с которой он взаимодействует. Это явление характеризуется коэффициентами охлаждения (нагрева) ηt и осушения (увлажнения) ηd воздуха, которые рассчитываются из следующих уравнений:
  | (6.30) |
где t1, d1 –– температура и влагосодержание воздуха на входе в аппарат для его обработки либо в среду взаимодействия;
t2, d2 –– те же параметры при выходе воздуха из аппарата либо среды;
tf, df –– параметры воздуха, равновесного с поверхностью аппарата либо среды.
Если заданы значения коэффициентов ηt либо ηd и известны начальные параметры воздуха и состояние поверхности либо среды, с которыми он взаимодействует, то можно с помощью уравнений (6.30) определить параметры воздуха в конце процесса.




