цепи с сосредоточенными параметрами
Электрические цепи с сосредоточенными и распределенными параметрами
Электрические цепи с сосредоточенными и распределенными параметрами
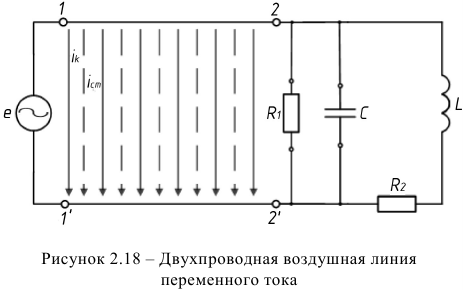
Рассмотренные в предыдущих параграфах пассивные идеальные элементы позволяют учитывать основные физические явления, протекающие в сложных электротехнических устройствах. Рассмотрим в качестве примера двухпроводную воздушную линию, соединяющую источник переменной ЭДС и приемник энергии (рисунок 2.18).
В соединительных проводах следует учитывать в общем случае четыре явления.
Электрическая цепь, в которой электрические сопротивления и проводимости, индуктивности и электрические емкости распределены вдоль линии, называют электрической цепью (линией) с распределенными параметрами.
Кроме приведенного примера к электрическим линиям с распределенными параметрами можно отнести реостаты, реальные индуктивные катушки и конденсаторы.
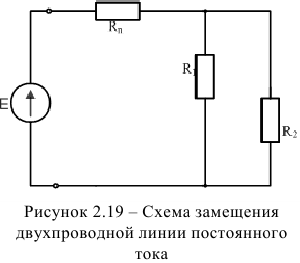
Далеко не во всех случаях необходимо учитывать все физические явления, происходящие в цепях переменного тока, что существенно упрощает задачу. Так, если в предыдущем примере величина напряжения источника питания малая, токи короны исчезают, а при постоянном характере ЭДС во времени исчезают токи электрического смещения и ЭДС самоиндукции. Схема замещения двухпроводной воздушной линии постоянного тока принимает упрощенный вид (рисунок 2.19), где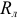 
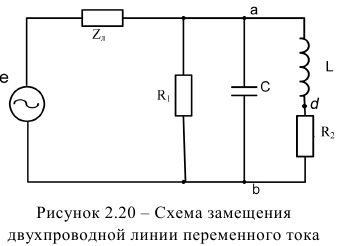
— резистор, учитывающий сопротивление току соединительного прямого и обратного проводов при малых значениях длины.
Схема замещения двухпроводной линии переменного тока с допущениями предыдущего примера представлена на рисунке 2.20, где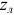 
— сопротивление прямого и обратного проводов соединительного провода.
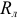
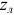
Не трудно заметить в схемах на рисунках 2.19 и 2.20 линия представлена в виде сосредоточенного сопротивления или .
Токи электрического смещения существуют только на участке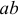 
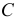
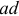
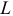
между обкладками конденсатора (рисунок 2.20), т.е. в этом участке сосредоточена емкость 
цепи. Наконец, предположим, что переменный магнитный поток индуцирует ЭДС только в катушке на участке 
, т.е., что в этом участке сосредоточена вся индуктивность 
цепи.
Электрические цепи, имеющие сложную конфигурацию и содержащие сосредоточенные резисторы, проводимости, индуктивности и электрические емкости только на отдельных участках и величина тока и потенциала, в общем случае, при переходе от одной точки к рядом расположенной непрерывно не изменяются для одного момента времени, называются электрическими цепями с сосредоточенными параметрами.
Приняв сделанные допущения, мы получаем возможность рассматривать теорию электрических цепей с сосредоточенными параметрами, охватывающую большой класс реальных электрических цепей, за исключением длинных линий передачи энергии и протяженных линий связи.
Электрическую цепь можно рассматривать как цепь с сосредоточенными параметрами, если изменения напряжений и токов в соединительных проводах цепи столь малы, что за время распространения электромагнитной волны вдоль всей цепи в любом направлении изменения величин напряжений и токов остаются малыми.
Эта страница взята со страницы задач по электротехнике:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Цепи с распределенными и с сосредоточенными параметрами
Если электрическая цепь содержит хотя бы один элемент с распределенными параметрами, то эта цепь называется цепью с распределенными параметрами. В противном случае цепь с сосредоточенными параметрами.
Элемент с сосредоточенными параметрами – это такой элемент, размеры которого не влияют на физические процессы в нем. К элементам с распределенными параметрами относятся линии передач, антенны. Если размеры элемента влияют на физические процессы, то это элемент с распределенными параметрами. В основном большинство элементов будем считать элементами с сосредоточенными параметрами.
Все высказанные выше определения достаточно условны. Один и тот же элемент в той или иной степени описания процесса на нем может быть отнесен к линейным или нелинейным, с распределенными или сосредоточенными параметрами.
В дальнейшем мы будем изучать линейные цепи с сосредоточенными параметрами.
Электрическая схема
Графическое изображение электрической цепи называется электрической схемой. На электрических схемах различают 3 элемента:
1. Ветвь – это последовательное соединение элементов, по которым протекает один и тот же ток.
2. Узел – это место электрической схемы, где сходится 3 и более ветвей.
3. Контур – это замкнутый участок цепи.
— ветви;
— узлы;
— замкнутые контуры.
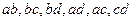
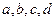
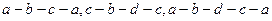
Число независимых контуров – это минимальное количество контуров, из которых может быть составлена рассматриваемая схема.
Обозначим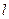 
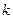
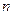
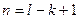
— число ветвей, 
— число узлов, 
— число независимых контуров, которое определяется по формуле 
.
Положительные направления токов, падений напряжений и э.д.с.
Обычно при анализе электрических цепей произвольно выбирается положительное направление токов в ветвях. Затем в зависимости от выбранных положительных направлений токов определяются положительные направления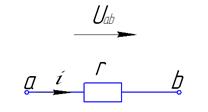 
падений напряжений на элементах. Рассмотрим отдельные элементы.
Это значит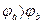 
, 
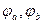
— потенциалы точек а и b.
Падение напряжений – это разность потенциалов, т.е.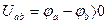 
, 
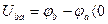
. То же самое будет на катушке индуктивности и конденсаторе.
Таким образом, положительное направление падения напряжения на пассивных элементах совпадает с положительным направлением тока через них.
Рассмотрим активный элемент – источник э.д.с.
, — потенциалы точек а и b.Тогда 
, 
.
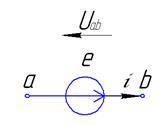
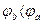
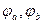
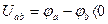
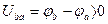
Таким образом, положительное направление падения напряжения на источнике э.д.с. противоположно положительному направлению э.д.с.
Пример:
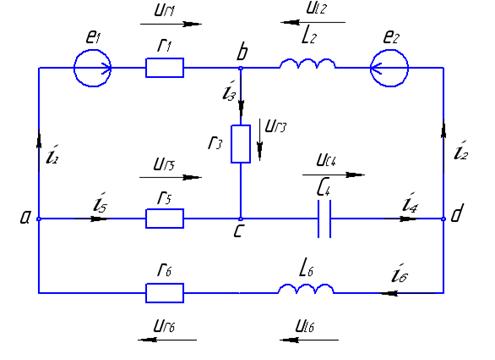
2.2 Электрические цепи с сосредоточенными параметрами.
Пассивные электрические цепи могут быть с сосредоточенными и распределенными параметрами.
Цепь состоит из источников R,L,C и соединительных проводов.
Если не выполнено хотя бы одно из перечисленных условий, то цепь следует рассматривать как цепь с распределенными параметрами.
Свойства цепи с сосредоточенными параметрами:
1)Если в данной цепи провести ряд сечений и включить в данное сечение А, то ток во всех точках в один и тот же момент окажется одинаковым.
2)Такая цепь не излучает в окружающее пространство электромагнитную энергию, все процессы сосредоточены внутри цепи.
Возникает вопрос: как разбивать схему для анализа?
В данной схеме, как источник u(t) поставляющий энергию в цепь, так и расходующий её пассивный элемент могут рассматриваться либо как элементы, в ходящие в состав данной цепи, либо как внешние по отношению к ней. В простейших случаях резистор считают элементом цепи, а источник внешним по отношению к ней.
Если электрическая цепь подключается к внешним элементам в двух точках (точка 1и 1’ на рисунке 2.1), то она называется двухполюсной.
Схему 2.1 можно считать как 2 двухполюсника
2.3 Электрические цепи с распределенными параметрами
Линия передает часть энергии в окружающее пространство в виде излучения.
рис 2.2
В цепи с сосредоточенными параметрами в любом сечении в один и тот же момент времени будет один и тот же ток, а в цепи с распределенными параметрами в разных сечениях в один и тот же момент времени будет разный ток.