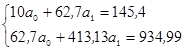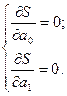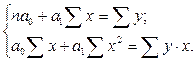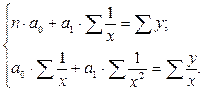укажите метод с помощью которого рассчитываются значения параметров уравнения регрессии

Определение параметров уравнения регрессии

Для определения параметров уравнения регрессии применяют метод наименьших квадратов (МНК). Метод был предложен К. Гауссом (1777 – 1855) и А. М. Лежандром (1752 – 1833) независимо друг от друга.

Сущность метода наименьших квадратов заключается в том, что отыскиваются такие значения параметров уравнения регрессии, при которых сумма квадратов отклонений фактических значений результативного признака от теоретических будет наименьшей из всех возможных, т.е.

, (8.5)

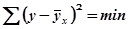
где у – фактические значения результативного признака;

– теоретические значения результативного признака.

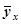
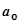
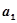
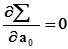
Для нахождения минимума функции следует приравнять к нулю частные производные по и :

и .(8.6)

Рассмотрим, как определяются параметры уравнения регрессии для различных видов аналитических функций.

1. Уравнение прямой:

,(8.7)

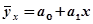
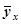
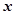
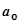
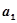
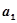
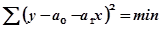
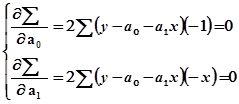
где – теоретическое значение результативного признака;

–значениефакторного признака;

и –параметры уравнения прямой;

–коэффициент регрессии(пропорциональности), характеризующий изменение среднего значения результативного признака при изменении факторного признака на единицу собственного измерения.

,(8.8)

(8.9)

После преобразования получим систему нормальных уравнений:

(8.10)

(8.11)

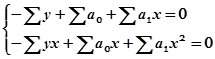
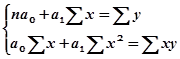
гдеn– число пар взаимосвязанных признаков.

По эмпирическим данным необходимо рассчитать все приведенные в формулах суммы и подставив их в систему уравнений, найти параметры искомой прямой.

Систему можно решить методом определителей:

; (8.12)

; (8.13)

. (8.14)

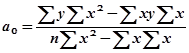
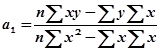
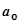
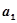
Значения параметров и подставляют в уравнение регрессии и находят теоретические значения результативного признака, которые показывают, каким теоретически должен быть средний размер результативного признака при данном размере факторного признака.

Пример 8.1. Построим линейное уравнение регрессии по данным табл. 8.1 и определим зависимость объема продукции от стоимости основных производственных фондов.

Расчетная таблица для определения параметров

Линейного уравнения регрессии

Номер пред-приятия	Объем продукции, млн. руб.	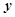Стоимость основных производственных фондов, млн. руб.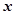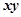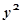
12,0	4,5	20,25	54,00	144,00	12,48
12,7	4,7	22,09	59,69	161,29	12,71
13,2	4,9	24,01	64,68	174,24	12,94
14,0	5,2	27,04	72,80	196,00	13,29
13,8	6,0	36,00	82,80	190,44	14,23
15,0	6,5	42,25	97,50	225,00	14,81
15,5	6,8	46,24	105,40	240,25	15,16
14,8	7,2	51,84	106,56	219,04	15,62
16,4	7,9	62,41	129,56	268,96	16,44
18,0	9,0	81,00	162,00	324,00	17,72
Итого	145,4	62,7	413,13	934,99	2143,22	145,4

1. Линейное уравнениерегрессии:

.

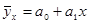
2. Система нормальных уравнений:

3. Определение параметров линейного уравнения регрессии:

Поделим каждое уравнение на соответствующие коэффициенты при 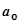: первое уравнение – на 10, второе – на 62,7:

Вычтем из второго уравнения первое. Получим:

;

; .

;

.

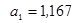
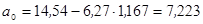
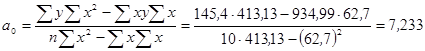
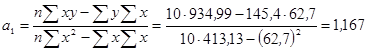
Линейное уравнение регрессии в числовом виде:

.

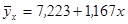
Коэффициент регрессии ( ) показывает, что при увеличении стоимости основных производственных фондов на 1 млн. руб. объем продукции в среднем будет увеличиваться на 1,167 млн. руб.

Измерение тесноты связи

Для измерения тесноты связи при линейной зависимости используются: линейный коэффициент корреляции, коэффициент детерминации и коэффициент эластичности.

1. Линейный коэффициент корреляции. В 1889 г. Френсис Гальтон высказал мысль о коэффициенте, который мог бы измерить тесноту связи. В начале 90-х годов XІX в. К. Пирсон, Ф. Эджворт и Велдон получили формулу коэффициента корреляции.

Линейным коэффициентом корреляцииназывается среднее произведение отклонений вариантов взаимосвязанных признаков от их средних величин, разделенное на произведение их средних квадратических отклонений.

.(8.21)

,(8.22)

где ; ; ;

; .

;(8.23)

;

.(8.24)

.(8.25)

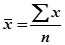
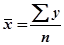
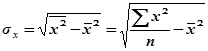
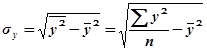
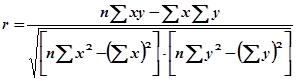
Четвертая формула.Коэффициент корреляции можно выразить через коэффициент регрессии:

.(8.26)

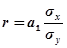
Решим в общем виде систему нормальных уравнений:

(8.27)

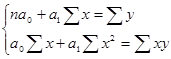
Поделим каждое уравнение на n:

(8.28)

Поделим второе уравнение на :

(8.29)

Вычтем из второго уравнения первое:

.(8.30)

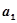
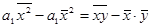
Определим параметр (коэффициент регрессии):

;(8.31)

.(8.32)

Выразим коэффициент корреляцииrчерез коэффициент регрессии :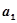

.(8.33)

Выведем дополнительные формулы для определения параметров уравнения регрессии. Для этого:

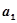
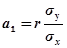
— выразим коэффициент регрессии через коэффициент корреляции r:

.(8.34)

— из первого уравнения системы уравнений (8.29) найдем параметр: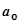

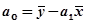
.(8.35)

Параметры линейного уравнения регрессии можно определить по формулам:

;(8.36)

.(8.37)

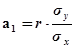
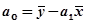
Линейный коэффициент корреляции изменяется в пределах:

. (8.38)

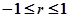
Если r = 0 – связь между признаками отсутствует;

r = 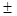1 – связь между признаками функциональная;

Источник

Оценка параметров линейного регрессионного уравнения

Для оценки параметров регрессионного уравнения наиболее часто используют метод наименьших квадратов (МНК), в основе которого лежит предположение о независимости наблюдений исследуемой совокупности. Сущность данного метода заключается в нахождении параметров модели (α, β), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:

В итоге получаем систему нормальных уравнений:

Эту систему можно записать в виде:

_{Решая данную систему линейных уравнений с двумя неизвестными получаем оценки наименьших квадратов:}

_{В уравнениях регрессии параметр α показывает усредненное влияние на результативный признак неучтенных факторов, а параметр β – коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу.}

_{Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:}

_{где – коэффициент регрессии в уравнении связи;}

– среднее квадратическое отклонение соответствующего статистически существенного факторного признака.

_{Имеются следующие данные о размере страховой суммы и страховых возмещений на автотранспортные средства одной из страховых компаний.}

_{Зависимость между размером страховых возмещений и страховой суммой на автотранспорт}

_{Объем страхового возмещения (тыс.долл.), Yi}

_{Стоимость застрахованного автомобиля (тыс.долл.), X i}

Источник

Сущность регрессионного анализа. Уравнение регрессии. Метод наименьших квадратов

Регрессионный анализ заключается в определении аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения. До регрессионного анализа следует проводить корреляционный анализ, в процессе которого оценивается степень тесноты статистической связи между исследуемыми переменны­ми. От степени тесноты связи зависит прогностическая сила регрессион­ной модели.

Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака от факторных признаков.

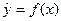
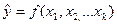
Уравнение регрессии или модель связи социально-экономических явлений выражается функцией. Различают парную () и множественную () регрессии.

Парная регрессий описывает связь между двумя признаками (результативным и факторным). Множественная регрессия описывает связь между результативным признаком и двумя и более факторными признаками.

Изучение модели парной регрессии является базовым во всем курсе эконометрики. Обычно она применяется в том случае, когда из всего круга факторов, влияющих на результат, можно выделить один, оказывающий наиболее сильное воздействие. Он и берется в качестве объясняющей переменной х.

Представим, что есть два ряда данных:

где n – число наблюдений.

Каждое из наблюдений характеризуется двумя переменными x_i, y_i. Число наблюдений n должно в шесть-семь раз превышать число параметров при переменной х в уравнении регрессии. Таким образом, для изучения линейной регрессии число наблюдений должно быть не менее семи.

В парной линейной регрессии связь между переменными определяется следующим образом:

,

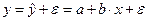
где у – зависимая (объясняемая) переменная, реальная, фактическая, эмпирическая;

х – независимая (объясняющая) переменная;

– зависимая переменная, рассчитанная по уравнению регрессии, теоретическая;

а, b – константы, параметры уравнения линейной регрессии;

– случайная компонента, возмущение.

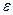
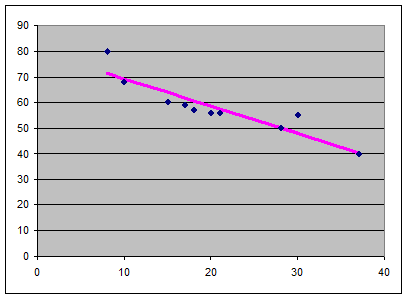
Каждую пару наблюдений (х_i;y_i) можно представить в виде точки на плоскости. Такое графическое изображение наблюдений называется полем корреляции или диаграммой рассеяния. Выбранный тип функции (прямая, парабола, гипербола и т.д.) должен проходить через большее количество точек или как можно ближе к ним.

В каждом из наблюдений величину случайной компоненты можно определить как разность между фактическим значением результата и рассчитанным по уравнению регрессии:

.

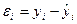
Если на графике все точки совпадут с линией регрессии, то между результативным признаком у и фактором х существует функциональная зависимость, и выполняется равенство 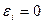для каждого наблюдения i=1,2,…,n.

Данные, которые описывают экономические процессы, не могут иметь строгую функциональную зависимость, поскольку на результативный признак в экономике влияет большое количество факторов и случайных процессов, и все они не могут быть учтены в модели.

В парной регрессии выбор вида математической функции 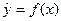может быть осуществлен с помощью следующих методов:

— графического (с помощью построения поля корреляции и подбора функции, график которой проходит через большее количество точек или как можно ближе к ним);

— аналитического (исходя из экономической теории изучаемой взаимосвязи и опыта подобных предыдущих исследований);

— экспериментального (посредством перебора нескольких функций, построения нескольких уравнений регрессии и выбора того уравнения, при котором остаточная дисперсия минимальна).

После того как выбран вид уравнения регрессии (прямая линия, парабола, гипербола и т.д.) находят значения параметров модели, для линейной регрессии – это а₀ и а₁. Для этого используют метод наименьших квадратов. В основу этого метода положена идея минимизации суммы квадратов отклонений фактических значений у от их выравненных (теоретических) значений , т.е.

,

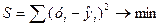
где у_i – фактические значения результативного признака;

– теоретические значения результативного признака, найденные по уравнению регрессии.

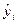
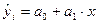
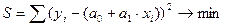
Если регрессия линейная , то

.

Рассматривая сумму S в качестве функции параметров а₀ и а₁ (значения х_i и у_i в функции S являются постоянными величинами), определяют частные производные по а₀ и а₁ и приравнивают их к нулю, поскольку в точке экстремума производная функции равна нулю:

Так, если связь между признаками линейная, то система уравнений для нахождения параметров уравнения регрессии примет вид:

После решения системы относительно а₀ и а₁ находят уравнение регрессии .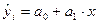

Если связь между признаками у и х описывается уравнением параболы 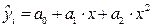, то система нормальных уравнений примет вид:

Если связь описывается уравнением гиперболы 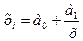, система нормальных уравнений следующая:

Вернемся к парной линейной регрессии. Решая систему уравнений относительно а и b, находят значения указанных параметров. Можно также воспользоваться следующими формулами для определения параметров а и b:

и .

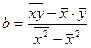
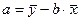
В Excel параметры а и b можно вычислить с помощью функции = ЛИНЕЙН, задав известные значения у и значения х.

Правильность расчетов параметров уравнения регрессии может быть проверена с помощью сравнения сумм:

.

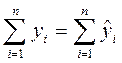
После определения параметров уравнения регрессии а и b записывают уравнение в окончательном виде, например .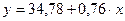

Параметр b (коэффициент при х) определяет, на сколько в среднем изменится у при изменении факторного признака на единицу.

Чем больше величина коэффициента регрессии b, тем значительнее влияние данного факторного признака на моделируемый результативный.

Знак коэффициента регрессии говорит о характере влияния фактора на результативный признак.

Экономическая интерпретация параметров линейного уравнения регрессии дополняется расчетом коэффициента эластичности:

.

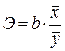
Этот коэффициент показывает, на сколько процентов в среднем изменится у при изменении фактора х на 1%.

Источник