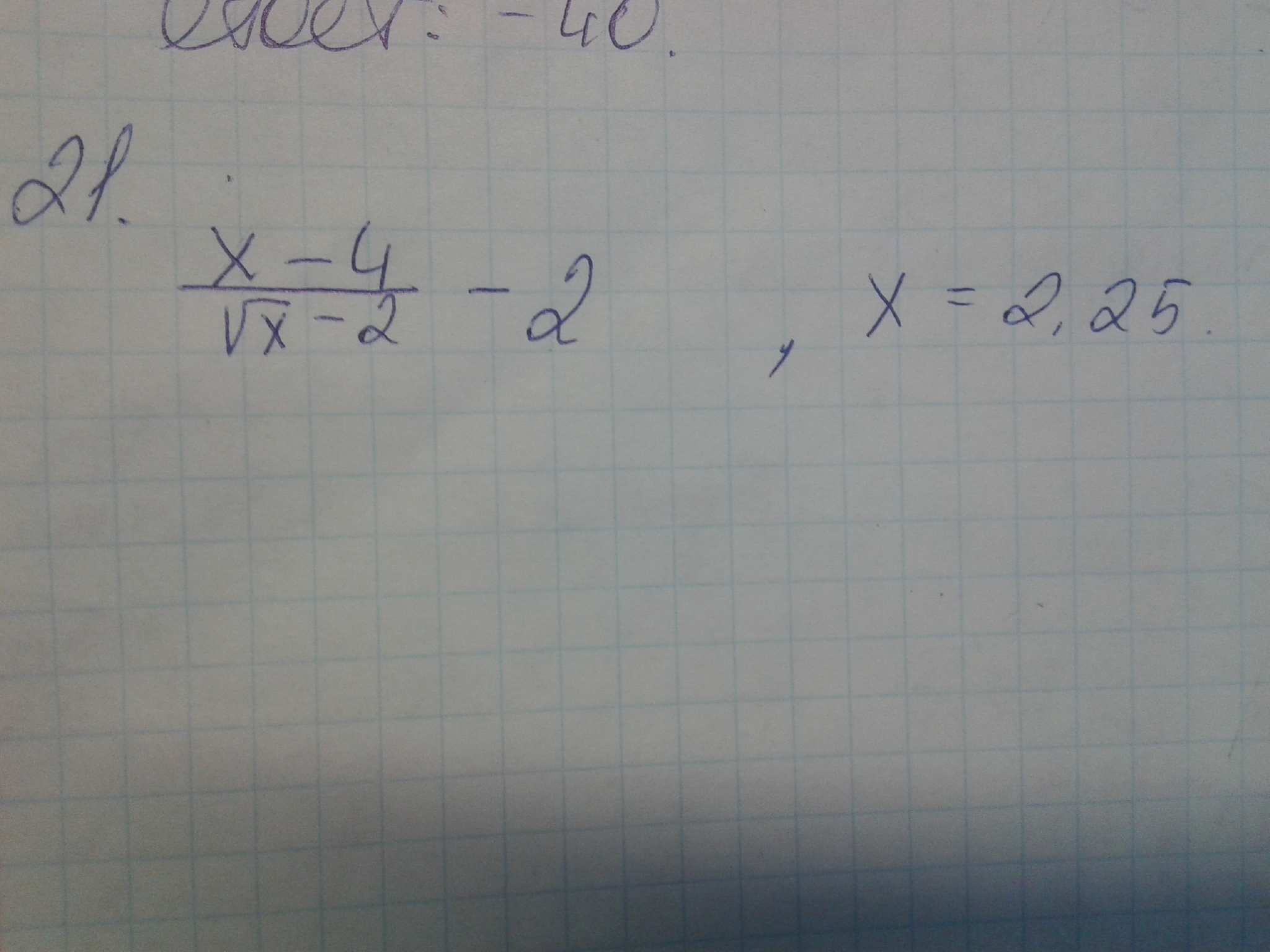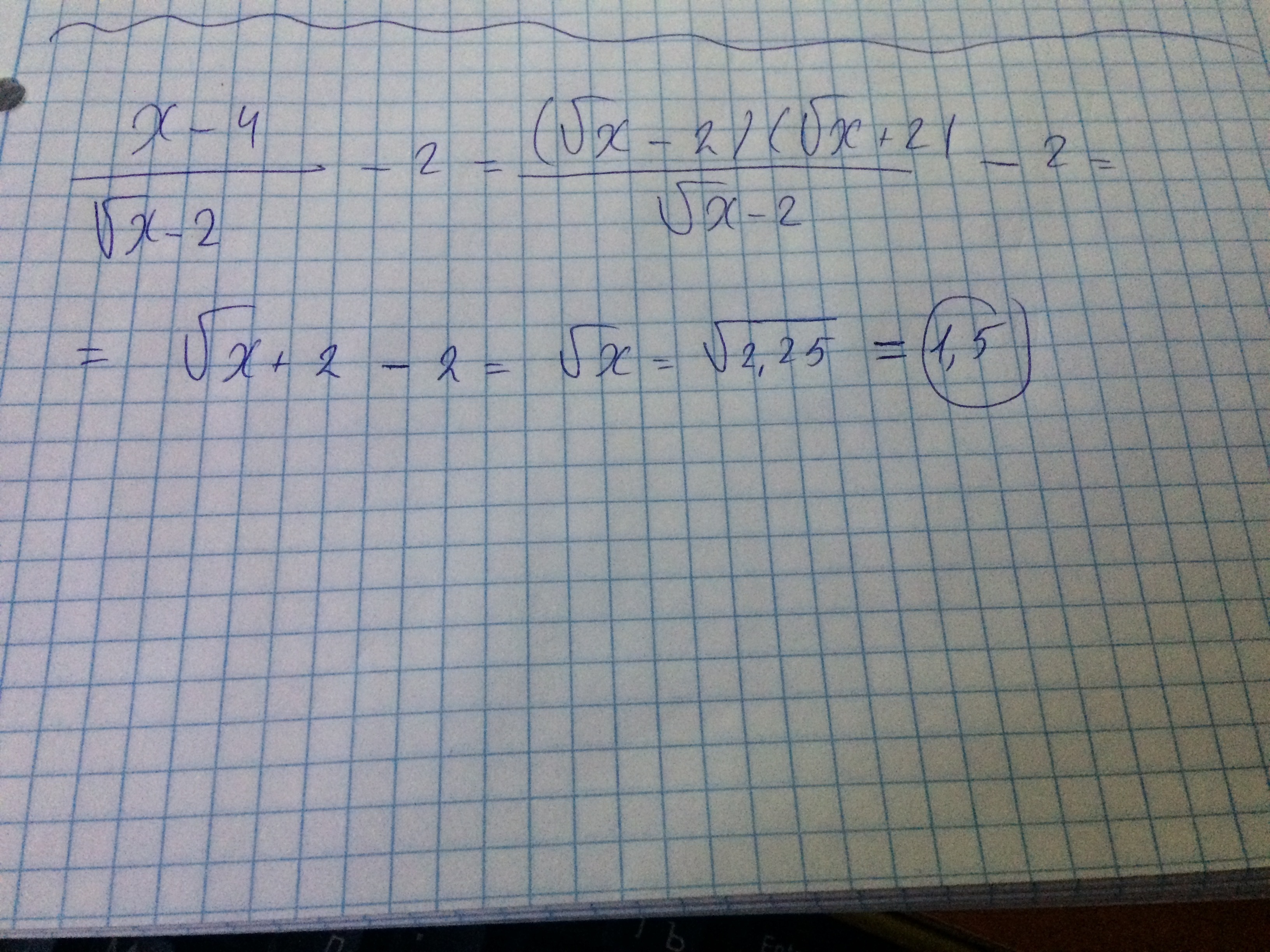упростить выражение и вычислить его при заданном значении параметра при а 95

Упростить выражение

Что значит упростить выражение

Когда говорят упростить выражение, подразумевают конкретные математические действия с этим выражением, в результате чего оно примет иной вид.

Такими действиями могут быть раскрытие скобок, внесение и вынесение множителя за скобку, деление (сокращение), умножение, возведение в степень, приведение дробей к общему знаменателю и много других операций.

При этом часто используют формулы сокращенного умножения и теоремы, а в тригонометрии от простых формул приведения до самых сложных тригонометрических выражений.

Чем старше школьник, тем больше формул он знает и обладает богатым арсеналом математических действий.

В чем смысл таких действий

Задачи на упрощение выражений встречаются с самых младших классов. Дети сами того не осознавая, учатся шевелить мозгами в нужном направлении, чтобы преобразовать одно выражение в другое.

Разумеется, все задания составляются таким образом, что в любом случае они приводятся к более простому виду или подходящему для дальнейших операций.

Однако, при таком подходе теряется общий смысл поставленной задачи.

Когда ученик слышит, что надо что-то упростить, то машинально начинает перебирать всевозможные математические действия в голове, не задаваясь вопросом, а для чего упрощать?

Приведем наглядный пример

Кто теперь скажет, что раскрыть скобки, затем подставить a=⅔ и b=⅓, а затем вычислить ответ, это легче, чем сразу найти a+b=⅔+⅓=1? После этого возводи единицу хоть в сотую степень!

Итак, главная цель задач на упрощение выражений в том, чтобы научить вас применять те или иные математические действия над выражениями.

Это обязательно нужно уметь делать. Но более важная проблема в том, чтобы научиться применять необходимые действия в нужный момент и воспользоваться результатом преобразования.

Благо есть онлайн калькуляторы упрощения выражений, например, такой как наш, с помощью которого можно проверить свои вычислительные результаты.

Источник

Упростите выражение и вычислите его значение :

Вычислите значение выражения :

Вычислите значение выражения?

Вычислите значение выражения.

Вычислите значение выражения?

Вычислите значение выражения.

Упростите выражение и найдите его значение :

Вычислите его значение при y = 417.

Упростите выражение и найдите его значение?

Упростите выражение и найдите его значение.

Упростить выражение и найти значение?

Упростить выражение и найти значение.

Упростить выражение и вычислить его значение

Найдите значение выражения :

Упростите выражение и вычислите его значение, если x = 9?

Упростите выражение и вычислите его значение, если x = 9.

Упростите выражение и вычислите его значение ПодробноПожалуйста?

Упростите выражение и вычислите его значение Подробно

Источник