В чем измеряется программное обеспечение
Измерение программного обеспечения
Основа для измерения программного обеспечения основана на трех принципах:
Классификация сущностей, подлежащих проверке
В программной инженерии существует в основном три класса сущностей. Они —
Все эти объекты имеют как внутренние, так и внешние объекты.
Внутренние атрибуты — это те, которые могут быть измерены исключительно с точки зрения самого процесса, продукта или ресурсов. Например: размер, сложность, зависимость между модулями.
Внешние атрибуты — это те, которые могут быть измерены только в отношении его связи с окружающей средой. Например: общее количество сбоев, с которыми столкнулся пользователь, время, необходимое для поиска в базе данных и получения информации.
Внутренние атрибуты — это те, которые могут быть измерены исключительно с точки зрения самого процесса, продукта или ресурсов. Например: размер, сложность, зависимость между модулями.
Внешние атрибуты — это те, которые могут быть измерены только в отношении его связи с окружающей средой. Например: общее количество сбоев, с которыми столкнулся пользователь, время, необходимое для поиска в базе данных и получения информации.
Различные атрибуты, которые могут быть измерены для каждого из объектов, следующие:
Процессы
Процессы представляют собой наборы программных действий. Ниже приведены некоторые внутренние атрибуты, которые можно измерить непосредственно для процесса:
Продолжительность процесса или одного из его действий
Усилия, связанные с процессом или одним из его видов деятельности
Количество инцидентов определенного типа, возникающих в ходе процесса или одного из его действий
Продолжительность процесса или одного из его действий
Усилия, связанные с процессом или одним из его видов деятельности
Количество инцидентов определенного типа, возникающих в ходе процесса или одного из его действий
Различные внешние атрибуты процесса — это стоимость, управляемость, эффективность, качество и стабильность.
Товары
Продукты — это не только элементы, которые руководство обязуется предоставить, но также любые артефакты или документы, созданные в течение жизненного цикла программного обеспечения.
Различные внутренние атрибуты продукта — это размер, усилия, стоимость, спецификация, длина, функциональность, модульность, повторное использование, избыточность и синтаксическая корректность. Среди этих размеров, усилия и стоимость относительно легко измерить, чем другие.
Различные внешние атрибуты продукта — это удобство использования, целостность, эффективность, тестируемость, возможность повторного использования, переносимость и совместимость. Эти атрибуты описывают не только код, но и другие документы, которые поддерживают усилия по разработке.
Ресурсы
Это объекты, необходимые для процесса деятельности. Это может быть любой вход для производства программного обеспечения. Он включает персонал, материалы, инструменты и методы.
Различными внутренними атрибутами для ресурсов являются возраст, цена, размер, скорость, объем памяти, температура и т. Д. Различными внешними атрибутами являются производительность, опыт, качество, удобство использования, надежность, комфорт и т. Д.
Определение соответствующих целей измерения
Конкретное измерение будет полезно, только если оно поможет понять процесс или один из его результатов. Улучшение процесса или продуктов может быть выполнено только тогда, когда в проекте четко определены цели для процессов и продуктов. Ясное понимание целей может быть использовано для создания предлагаемых метрик для данного проекта в контексте структуры зрелости процесса.
Парадигма цель-вопрос-метрика (GQM)
Подход GQM обеспечивает структуру, включающую следующие три этапа:
Перечисление основных целей проекта разработки или сопровождения
Вывод вопросов из каждой цели, на которые необходимо ответить, чтобы определить, достигаются ли цели
Решите, что должно быть измерено, чтобы иметь возможность адекватно отвечать на вопросы
Перечисление основных целей проекта разработки или сопровождения
Вывод вопросов из каждой цели, на которые необходимо ответить, чтобы определить, достигаются ли цели
Решите, что должно быть измерено, чтобы иметь возможность адекватно отвечать на вопросы
Чтобы использовать парадигму GQM, сначала мы выражаем общие цели организации. Затем мы генерируем вопросы так, чтобы ответы были известны, чтобы мы могли определить, достигаются ли цели. Позже, проанализируйте каждый вопрос с точки зрения того, какое измерение нам нужно, чтобы ответить на каждый вопрос.
Типичные цели выражаются с точки зрения производительности, качества, риска, удовлетворенности клиентов и т. Д. Цели и вопросы должны строиться с точки зрения их аудитории.
Чтобы составить цели, вопросы и показатели, Basili & Rombach предоставили серию шаблонов.
Цель — Чтобы (охарактеризовать, оценить, предсказать, мотивировать и т. Д.) (Процесс, продукт, модель, метрика и т. Д.), Чтобы понять, оценить, управлять, спроектировать, выучить, улучшить и т. Д. Пример : охарактеризовать продукт для того, чтобы выучить его.
Цель — Чтобы (охарактеризовать, оценить, предсказать, мотивировать и т. Д.) (Процесс, продукт, модель, метрика и т. Д.), Чтобы понять, оценить, управлять, спроектировать, выучить, улучшить и т. Д. Пример : охарактеризовать продукт для того, чтобы выучить его.
Измерение и улучшение процесса
Обычно измерение полезно для —
В зависимости от уровня зрелости процесса, указанного SEI, тип измерения и программа измерения будут отличаться. Ниже приведены различные программы измерения, которые могут применяться на каждом уровне зрелости.
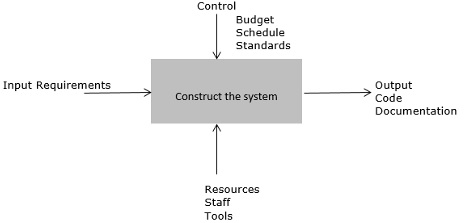
На этом уровне входы плохо определены, а выходы ожидаемы. Переход от входа к выходу не определен и не контролируется. Для этого уровня зрелости процесса, базовые измерения необходимы, чтобы обеспечить отправную точку для измерения.
Уровень 2: Повторяемый
На этом уровне входные и выходные данные процесса, ограничения и ресурсы являются идентифицируемыми. Повторяемый процесс может быть описан следующей диаграммой.
Мерами ввода могут быть размер и изменчивость требований. Результат может быть измерен с точки зрения размера системы, ресурсов с точки зрения усилий персонала и ограничений с точки зрения затрат и графика.
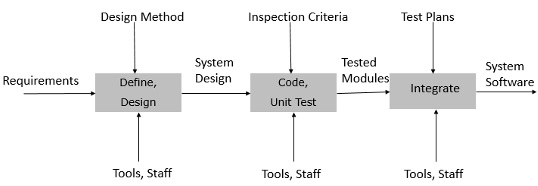
Уровень 3: Определен
На этом уровне определены промежуточные действия, а их входы и выходы известны и понятны. Простой пример определенного процесса описан на следующем рисунке.
Вклад в промежуточные действия и выход из них могут быть изучены, измерены и оценены.
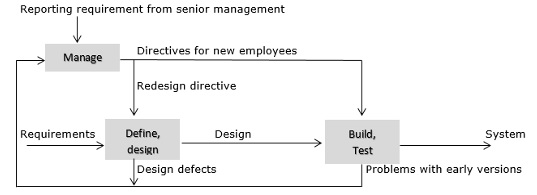
Уровень 4: Управляемый
На этом уровне отзывы о ранних действиях проекта могут использоваться для определения приоритетов для текущей деятельности, а затем и для деятельности проекта. Мы можем измерить эффективность процесса деятельности. Измерение отражает характеристики всего процесса и взаимодействия между основными видами деятельности и между ними.
Уровень 5: Оптимизация
На этом уровне показатели действий используются для улучшения процесса путем удаления и добавления операций процесса и динамического изменения структуры процесса в ответ на обратную связь измерения. Таким образом, изменение процесса может повлиять на организацию и проект, а также на процесс. Процесс будет действовать как датчики и мониторы, и мы можем существенно изменить процесс в ответ на предупреждающие знаки.
На данном уровне зрелости мы можем собрать измерения для этого уровня и всех уровней ниже него.
Определение уровня зрелости
Процесс зрелости предлагает измерять только то, что видно. Таким образом, сочетание зрелости процесса с GQM обеспечит наиболее полезные меры.
На уровне 2 требования четко определены, и может быть собрана дополнительная информация, такая как тип каждого требования и количество изменений каждого типа.
На уровне 3 промежуточные действия определяются с критериями входа и выхода для каждого действия
На уровне 2 требования четко определены, и может быть собрана дополнительная информация, такая как тип каждого требования и количество изменений каждого типа.
На уровне 3 промежуточные действия определяются с критериями входа и выхода для каждого действия
Анализ целей и вопросов будет одинаковым, но показатель будет варьироваться в зависимости от срока погашения. Чем более зрелый процесс, тем богаче будут измерения. Парадигма GQM, в сочетании со зрелостью процесса, была использована в качестве основы для нескольких инструментов, которые помогают менеджерам в разработке программ измерения.
GQM помогает понять необходимость измерения атрибута, а зрелость процесса показывает, способны ли мы измерить его значимым образом. Вместе они обеспечивают контекст для измерения.
Программное обеспечение
1 Изучите материал страницы
2 Ответьте на вопросы теста ЗДЕСЬ
Программное обеспечение (англ. software) – это совокупность программ, обеспечивающих функционирование компьютеров и решение с их помощью задач предметных областей. Программное обеспечение (ПО) представляет собой неотъемлемую часть компьютерной системы, является логическим продолжением технических средств и определяет сферу применения компьютера.
ПО современных компьютеров включает множество разнообразных программ, которое можно условно разделить на три группы (рис. 3.1):
1. Системное программное обеспечение (системные программы);
2. Прикладное программное обеспечение (прикладные программы);
3. Инструментальное обеспечение (инструментальные системы).
Системное программное обеспечение (СПО) – это программы, управляющие работой компьютера и выполняющие различные вспомогательные функции, например, управление ресурсами компьютера, создание копий информации, проверка работоспособности устройств компьютера, выдача справочной информации о компьютере и др. Они предназначены для всех категорий пользователей, используются для эффективной работы компьютера и пользователя, а также эффективного выполнения прикладных программ.
Центральное место среди системных программ занимают операционные системы (англ. operating systems). Операционная система (ОС) – это комплекс программ, предназначенных для управления загрузкой, запуском и выполнением других пользовательских программ, а также для планирования и управления вычислительными ресурсами ЭВМ, т.е. управления работой ПЭВМ с момента включения до момента выключения питания. Она загружается автоматически при включении компьютера, ведет диалог с пользователем, осуществляет управление компьютером, его ресурсами (оперативной памятью, дисковым пространством и т.д.), запускает другие программы на выполнение и обеспечивает пользователю и программам удобный способ общения – интерфейс – с устройствами компьютера. Другими словами, операционная система обеспечивает функционирование и взаимосвязь всех компонентов компьютера, а также предоставляет пользователю доступ к его аппаратным возможностям.
ОС определяет производительность системы, степень защиты данных, выбор программ, с которыми можно работать на компьютере, требования к аппаратным средствам. Примерами ОС являются MS DOS, OS/2, Unix, Windows 9х, Windows XP.
Сервисные системы расширяют возможности ОС по обслуживанию системы, обеспечивают удобство работы пользователя. К этой категории относят системы технического обслуживания, программные оболочки и среды ОС, а также служебные программы.
Системы технического обслуживания – это совокупность программно-аппаратных средств ПК, которые выполняют контроль, тестирование и диагностику и используются для проверки функционирования устройств компьютера и обнаружения неисправностей в процессе работы компьютера. Они являются инструментом специалистов по эксплуатации и ремонту технических средств компьютера.
Для организации более удобного и наглядного интерфейса пользователя с компьютером используются программные оболочки операционных систем – программы, которые позволяют пользователю отличными от предоставляемых ОС средствами (более понятными и эффективными) осуществлять действия по управлению ресурсами компьютера. К числу наиболее популярных оболочек относятся пакеты Norton Commander (Symantec), FAR (File and Archive manageR) (Е.Рошаль).
Служебные программы ( утилиты, лат. utilitas – польза) – это вспомогательные программы, предоставляющие пользователю ряд дополнительных услуг по реализации часто выполняемых работ или же повышающие удобство и комфортность работы. К ним относятся:
программы-упаковщики (архиваторы), которые позволяют более плотно записывать информацию на дисках, а также объединять копии нескольких файлов в один, так называемый, архивный файл (архив);
антивирусные программы, предназначенные для предотвращения заражения компьютерными вирусами и ликвидации последствий заражения;
программы оптимизации и контроля качества дискового пространства;
программы восстановления информации, форматирования, защиты данных;
программы для записи компакт-дисков;
драйверы – программы, расширяющие возможности операционной системы по управлению устройствами ввода/вывода, оперативной памятью и т.д. При подключении к компьютеру новых устройств необходимо установить соответствующие драйверы;
коммуникационные программы, организующие обмен информацией между компьютерами и др.
Некоторые утилиты входят в состав операционной системы, а некоторые поставляются на рынок как самостоятельные программные продукты, например, многофункциональный пакет сервисных утилит Norton Utilities (Symantec).
Прикладное программное обеспечение (ППО) предназначено для решения задач пользователя. В его состав входят прикладные программы пользователей и пакеты прикладных программ (ППП) различного назначения .
Прикладная программа пользователя – это любая программа, способствующая решению какой-либо задачи в пределах данной проблемной области. Прикладные программы могут использоваться либо автономно, либо в составе программных комплексов или пакетов.
Пакеты прикладных программ (ППП) – это специальным образом организованные программные комплексы, рассчитанные на общее применение в определенной проблемной области и дополненные соответствующей технической документацией. Различают следующие типы ППП:
ППП общего назначения – универсальные программные продукты, предназначенные для автоматизации широкого класса задач пользователя. К ним относятся:
Текстовые редакторы (например, MS Word, Word Perfect, Лексикон);
Табличные процессоры (например, MS Excel, Lotus 1-2-3, Quattro Pro);
Системы динамических презентаций (например, MS Power Point, Freelance Graphics, Harvard Graphics);
Системы управления базами данных (например, MS Access, Oracle, MS SQL Server, Informix);
Графические редакторы (например, Сorel Draw, Adobe Photoshop);
Издательские системы (например, Page Maker, Venture Publisher);
Системы автоматизации проектирования (например, BPWin, ERWin);
Электронные словари и системы перевода (например, Prompt, Сократ, Лингво , Контекст);
Системы распознавания текста (например, Fine Reader, Cunei Form).
Системы общего назначения часто интегрируются в многокомпонентные пакеты для автоматизации офисной деятельности – офисные пакеты – Microsoft Office, StarOffice и др.
методо-ориентированные ППП, в основе которых лежит реализация математических методов решения задач. К ним относятся, например, системы математической обработки данных (Mathematica, MathCad, Maple), системы статистической обработки данных (Statistica, Stat).;
проблемно-ориентированные ППП предназначены для решения определенной задачи в конкретной предметной области. Например, информационно-правовые системы ЮрЭксперт, ЮрИнформ; пакеты бухгалтерского учета и контроля 1С: Бухгалтерия, Галактика, Анжелика; в области маркетинга –Касатка, Marketing Expert; банковская система СТБанк;
интегрированные ППП представляют собой набор нескольких программных продуктов, объединенных в единый инструмент. Наиболее развитые из них включают в себя текстовый редактор, персональный менеджер (органайзер), электронную таблицу, систему управления базами данных, средства поддержки электронной почты, программу создания презентационной графики. Результаты, полученные отдельными подпрограммами, могут быть объединены в окончательный документ, содержащий табличный, графический и текстовый материал. К ним относят, например, MS Works. Интегрированные пакеты, как правило, содержат некоторое ядро, обеспечивающее возможность тесного взаимодействия между составляющими.
Обычно пакеты прикладных программ имеют средства настройки, что позволяет при эксплуатации адаптировать их к специфике предметной области.
Транслятор (англ. translator – переводчик) – это программа-переводчик, которая преобразует программу с языка высокого уровня в программу, состоящую из машинных команд. Трансляторы реализуются в виде компиляторов или интерпретаторов, которые существенно различаются по принципам работы.
Компилятор (англ. compiler – составитель, собиратель) читает всю программу целиком, делает ее перевод и создает законченный вариант программы на машинном языке, который затем и выполняется. После компилирования получается исполняемая программа, при выполнении которой не нужна ни исходная программа, ни компилятор.
Интерпретатор (англ. interpreter – истолкователь, устный переводчик) переводит и выполняет программу строка за строкой. Программа, обрабатываемая интерпретатором, должна заново переводиться на машинный язык при каждом очередном ее запуске.
Откомпилированные программы работают быстрее, но интерпретируемые проще исправлять и изменять.
Программный код и его метрики

Одной из тем в программировании, к которым интерес периодически то появляется, то пропадает, является вопрос метрик кода программного обеспечения. В крупных программных средах время от времени появляются механизмы подсчета различных метрик. Волнообразный интерес к теме так выглядит потому, что до сих пор в метриках не придумано главного — что с ними делать. То есть даже если какой-то инструмент позволяет хорошо подсчитать некоторые метрики, то что с этим делать дальше зачастую непонятно. Конечно, метрики — это и контроль качества кода (не пишем большие и сложные функции), и «производительность» (в кавычках) программистов, и скорость развития проекта. Эта статья — обзор наиболее известных метрик кода программного обеспечения.
Введение
В статье приведен обзор 7 классов метрик и более 50 их представителей.
Будет представлен широкий спектр метрик программного обеспечения. Естественно, все существующие метрики приводить не целесообразно, большинство из них никогда не применяется на практике либо из-за невозможности дальнейшего использования результатов, либо из-за невозможности автоматизации измерений, либо из-за узкой специализации данных метрик, однако существуют метрики, которые применяются достаточно часто, и их обзор как раз будет приведен ниже.
В общем случае применение метрик позволяет руководителям проектов и предприятий изучить сложность разработанного или даже разрабатываемого проекта, оценить объем работ, стилистику разрабатываемой программы и усилия, потраченные каждым разработчиком для реализации того или иного решения. Однако метрики могут служить лишь рекомендательными характеристиками, ими нельзя полностью руководствоваться, так как при разработке ПО программисты, стремясь минимизировать или максимизировать ту или иную меру для своей программы, могут прибегать к хитростям вплоть до снижения эффективности работы программы. Кроме того, если, к примеру, программист написал малое количество строк кода или внес небольшое число структурных изменений, это вовсе не значит, что он ничего не делал, а может означать, что дефект программы было очень сложно отыскать. Последняя проблема, однако, частично может быть решена при использовании метрик сложности, т.к. в более сложной программе ошибку найти сложнее.
1. Количественные метрики
Прежде всего, следует рассмотреть количественные характеристики исходного кода программ (в виду их простоты). Самой элементарной метрикой является количество строк кода (SLOC). Данная метрика была изначально разработана для оценки трудозатрат по проекту. Однако из-за того, что одна и та же функциональность может быть разбита на несколько строк или записана в одну строку, метрика стала практически неприменимой с появлением языков, в которых в одну строку может быть записано больше одной команды. Поэтому различают логические и физические строки кода. Логические строки кода — это количество команд программы. Данный вариант описания так же имеет свои недостатки, так как сильно зависит от используемого языка программирования и стиля программирования [2].
Также к группе метрик, основанных на подсчете некоторых единиц в коде программы, относят метрики Холстеда [3]. Данные метрики основаны на следующих показателях:
n1 — число уникальных операторов программы, включая символы-
разделители, имена процедур и знаки операций (словарь операторов),
n2 — число уникальных операндов программы (словарь операндов),
N1 — общее число операторов в программе,
N2 — общее число операндов в программе,
n1′ — теоретическое число уникальных операторов,
n2′ — теоретическое число уникальных операндов.
Учитывая введенные обозначения, можно определить:
n=n1+n2 — словарь программы,
N=N1+N2 — длина программы,
n’=n1’+n2′ — теоретический словарь программы,
N’= n1*log2(n1) + n2*log2(n2) — теоретическая длина программы (для стилистически корректных программ отклонение N от N’ не превышает 10%)
V=N*log2n — объем программы,
V’=N’*log2n’ — теоретический объем программы, где n* — теоретический словарь программы.
L=V’/V — уровень качества программирования, для идеальной программы L=1
L’= (2 n2)/ (n1*N2) — уровень качества программирования, основанный лишь на параметрах реальной программы без учета теоретических параметров,
EC=V/(L’)2 — сложность понимания программы,
D=1/ L’ — трудоемкость кодирования программы,
y’ = V/ D2 — уровень языка выражения
I=V/D — информационное содержание программы, данная характеристика позволяет определить умственные затраты на создание программы
E=N’ * log2(n/L) — оценка необходимых интеллектуальных усилий при разработке программы, характеризующая число требуемых элементарных решений при написании программы
При применении метрик Холстеда частично компенсируются недостатки, связанные с возможностью записи одной и той же функциональности разным количеством строк и операторов.
Еще одним типом метрик ПО, относящихся к количественным, являются метрики Джилба. Они показывают сложность программного обеспечения на основе насыщенности программы условными операторами или операторами цикла. Данная метрика, не смотря на свою простоту, довольно хорошо отражает сложность написания и понимания программы, а при добавлении такого показателя, как максимальный уровень вложенности условных и циклических операторов, эффективность данной метрики значительно возрастает.
2. Метрики сложности потока управления программы
Следующий большой класс метрик, основанный уже не на количественных показателях, а на анализе управляющего графа программы, называется метрики сложности потока управления программ.
Перед тем как непосредственно описывать сами метрики, для лучшего понимания будет описан управляющий граф программы и способ его построения.
Пусть представлена некоторая программа. Для данной программы строится ориентированный граф, содержащий лишь один вход и один выход, при этом вершины графа соотносят с теми участками кода программы, в которых имеются лишь последовательные вычисления, и отсутствуют операторы ветвления и цикла, а дуги соотносят с переходами от блока к блоку и ветвями выполнения программы. Условие при построении данного графа: каждая вершина достижима из начальной, и конечная вершина достижима из любой другой вершины [4].
К сожалению, данная оценка не способна различать циклические и условные конструкции. Еще одним существенным недостатком подобного подхода является то, что программы, представленные одними и теми же графами, могут иметь совершенно разные по сложности предикаты (предикат — логическое выражение, содержащее хотя бы одну переменную).
Для исправления данного недостатка Г. Майерсом была разработана новая методика. В качестве оценки он предложил взять интервал (эта оценка еще называется интервальной) [V(G),V(G)+h], где h для простых предикатов равно нулю, а для n-местных h=n-1. Данный метод позволяет различать разные по сложности предикаты, однако на практике он почти не применяется.
Продолжая тему анализа управляющего графа программы, можно выделить еще одну подгруппу метрик — метрики Харрисона, Мейджела.
Данные меры учитывает уровень вложенности и протяженность программы.
Каждой вершине присваивается своя сложность в соответствии с оператором, который она изображает. Эта начальная сложность вершины может вычисляться любым способом, включая использование мер Холстеда. Выделим для каждой предикатной вершины подграф, порожденный вершинами, которые являются концами исходящих из нее дуг, а также вершинами, достижимыми из каждой такой вершины (нижняя граница подграфа), и вершинами, лежащими на путях из предикатной вершины в какую-нибудь нижнюю границу. Этот подграф называется сферой влияния предикатной вершины.
Приведенной сложностью предикатной вершины называется сумма начальных или приведенных сложностей вершин, входящих в ее сферу влияния, плюс первичная сложность самой предикатной вершины.
Функциональная мера (SCOPE) программы — это сумма приведенных сложностей всех вершин управляющего графа.
Функциональным отношением (SCORT) называется отношение числа вершин в управляющем графе к его функциональной сложности, причем из числа вершин исключаются терминальные.
SCORT может принимать разные значения для графов с одинаковым цикломатическим числом.
Метрика Пивоварского — очередная модификация меры цикломатической сложности. Она позволяет отслеживать различия не только между последовательными и вложенными управляющими конструкциями, но и между структурированными и неструктурированными программами. Она выражается отношением N(G) = v *(G) + СУММАPi, где v *(G) — модифицированная цикломатическая сложность, вычисленная так же, как и V(G), но с одним отличием: оператор CASE с n выходами рассматривается как один логический оператор, а не как n — 1 операторов.
Рi — глубина вложенности i-й предикатной вершины. Для подсчета глубины вложенности предикатных вершин используется число «сфер влияния». Под глубиной вложенности понимается число всех «сфер влияния» предикатов, которые либо полностью содержатся в сфере рассматриваемой вершины, либо пересекаются с ней. Глубина вложенности увеличивается за счет вложенности не самих предикатов, а «сфер влияния». Мера Пивоварского возрастает при переходе от последовательных программ к вложенным и далее к неструктурированным, что является ее огромным преимуществом перед многими другими мерами данной группы.
Мера Вудворда — количество пересечений дуг управляющего графа. Так как в хорошо структурированной программе таких ситуаций возникать не должно, то данная метрика применяется в основном в слабо структурированных языках (Ассемблер, Фортран). Точка пересечения возникает при выходе управления за пределы двух вершин, являющихся последовательными операторами.
Метод граничных значений так же основан на анализе управляющего графа программы. Для определения данного метода необходимо ввести несколько дополнительных понятий.
Пусть G — управляющий граф программы с единственной начальной и единственной конечной вершинами.
В этом графе число входящих вершин у дуг называется отрицательной степенью вершины, а число исходящих из вершины дуг — положительной степенью вершины. Тогда набор вершин графа можно разбить на две группы: вершины, у которых положительная степень =2.
Вершины первой группы назовем принимающими вершинами, а вершины второй группы — вершинами отбора.
Каждая принимающая вершина имеет приведенную сложность, равную 1, кроме конечной вершины, приведенная сложность которой равна 0. Приведенные сложности всех вершин графа G суммируются, образуя абсолютную граничную сложность программы. После этого определяется относительная граничная сложность программы:
где S0 — относительная граничная сложность программы, Sa — абсолютная граничная сложность программы, v — общее число вершин графа программы.
Существует метрика Шнейдевинда, выражающаяся через число возможных путей в управляющем графе.
3. Метрики сложности потока управления данными
Следующий класс метрик — метрики сложности потока управления данных.
Метрика Чепина: суть метода состоит в оценке информационной прочности отдельно взятого программного модуля с помощью анализа характера использования переменных из списка ввода-вывода.
Все множество переменных, составляющих список ввода-вывода, разбивается на 4 функциональные группы :
1. P — вводимые переменные для расчетов и для обеспечения вывода,
2. M — модифицируемые, или создаваемые внутри программы переменные,
3. C — переменные, участвующие в управлении работой программного модуля (управляющие переменные),
4. T — не используемые в программе («паразитные») переменные.
Поскольку каждая переменная может выполнять одновременно несколько функций, необходимо учитывать ее в каждой соответствующей функциональной группе.
Q = a1*P + a2*M + a3*C + a4*T,
где a1, a2, a3, a4 — весовые коэффициенты.
Весовые коэффициенты использованы для отражения различного влияния на сложность программы каждой функциональной группы. По мнению автора метрики, наибольший вес, равный 3, имеет функциональная группа C, так как она влияет на поток управления программы. Весовые коэффициенты остальных групп распределяются следующим образом: a1=1, a2=2, a4=0.5. Весовой коэффициент группы T не равен 0, поскольку «паразитные» переменные не увеличивают сложность потока данных программы, но иногда затрудняют ее понимание. С учетом весовых коэффициентов:
Метрика спена основывается на локализации обращений к данным внутри каждой программной секции. Спен — это число утверждений, содержащих данный идентификатор, между его первым и последним появлением в тексте программы. Следовательно, идентификатор, появившийся n раз, имеет спен, равный n-1. При большом спене усложняется тестирование и отладка.
Еще одна метрика, учитывающая сложность потока данных — это метрика, связывающая сложность программ с обращениями к глобальным переменным.
Пара «модуль-глобальная переменная» обозначается как (p,r), где p — модуль, имеющий доступ к глобальной переменной r. В зависимости от наличия в программе реального обращения к переменной r формируются два типа пар «модуль — глобальная переменная»: фактические и возможные. Возможное обращение к r с помощью p показывает, что область существования r включает в себя p.
Данная характеристика обозначается Aup и говорит о том, сколько раз модули Up действительно получали доступ к глобальным переменным, а число Pup — сколько раз они могли бы получить доступ.
Отношение числа фактических обращений к возможным определяется
Эта формула показывает приближенную вероятность ссылки произвольного модуля на произвольную глобальную переменную. Очевидно, что чем выше эта вероятность, тем выше вероятность «несанкционированного» изменения какой-либо переменной, что может существенно осложнить работы, связанные с модификацией программы.
На основе концепции информационных потоков создана мера Кафура. Для использования данной меры вводятся понятия локального и глобального потока: локальный поток информации из A в B существует, если:
1. Модуль А вызывает модуль В (прямой локальный поток)
2. Модуль В вызывает модуль А и А возвращает В значение, которое используется в В (непрямой локальный поток)
3. Модуль С вызывает модули А, В и передаёт результат выполнения модуля А в В.
Далее следует дать понятие глобального потока информации: глобальный поток информации из А в В через глобальную структуру данных D существует, если модуль А помещает информацию в D, а модуль В использует информацию из D.
На основе этих понятий вводится величина I — информационная сложность процедуры:
I = length * (fan_in * fan_out)2
Здесь:
length — сложность текста процедуры (меряется через какую-нибудь из метрик объёма, типа метрик Холстеда, Маккейба, LOC и т.п.)
fan_in — число локальных потоков входящих внутрь процедуры плюс число структур данных, из которых процедура берёт информацию
fan_out — число локальных потоков исходящих из процедуры плюс число структур данных, которые обновляются процедурой
Можно определить информационную сложность модуля как сумму информационных сложностей входящих в него процедур.
Следующий шаг — рассмотреть информационную сложность модуля относительно некоторой структуры данных. Информационная мера сложности модуля относительно структуры данных:
J = W * R + W * RW + RW *R + RW * (RW — 1)
W — число процедур, которые только обновляют структуру данных;
R — только читают информацию из структуры данных;
RW — и читают, и обновляют информацию в структуре данных.
Еще одна мера данной группы — мера Овиедо. Суть ее состоит в том, что программа разбивается на линейные непересекающиеся участки — лучи операторов, которые образуют управляющий граф программы.
Автор метрики исходит из следующих предположений: программист может найти отношение между определяющими и использующими вхождениями переменной внутри луча более легко, чем между лучами; число различных определяющих вхождений в каждом луче более важно, чем общее число использующих вхождений переменных в каждом луче.
Обозначим через R(i) множество определяющих вхождений переменных, которые расположены в радиусе действия луча i (определяющее вхождение переменной находится в радиусе действия луча, если переменная либо локальна в нём и имеет определяющее вхождение, либо для неё есть определяющее вхождение в некотором предшествующем луче, и нет локального определения по пути). Обозначим через V(i) множество переменных, использующие вхождения которых уже есть в луче i. Тогда мера сложности i-го луча задаётся как:
где DEF(vj) — число определяющих вхождений переменной vj из множества R(i), а ||V(i)|| — мощность множества V(i).
4. Метрики сложности потока управления и данных программы
Четвертым классом метрик являются метрики, близкие как к классу количественных метрик, классу метрик сложности потока управления программы, так и к классу метрик сложности потока управления данными (строго говоря, данный класс метрик и класс метрик сложности потока управления программы являются одним и тем же классом — топологическими метриками, но имеет смысл разделить их в данном контексте для большей ясности). Данный класс метрик устанавливает сложность структуры программы как на основе количественных подсчетов, так и на основе анализа управляющих структур.
Первой из таких метрик является тестирующая М-Мера [5]. Тестирующей мерой М называется мера сложности, удовлетворяющая следующим условиям:
Мера возрастает с глубиной вложенности и учитывает протяженность программы. К тестирующей мере близко примыкает мера на основе регулярных вложений. Идея этой меры сложности программ состоит в подсчете суммарного числа символов (операндов, операторов, скобок) в регулярном выражении с минимально необходимым числом скобок, описывающим управляющий граф программы. Все меры этой группы чувствительны к вложенности управляющих конструкций и к протяженности программы. Однако возрастает уровень трудоемкости вычислений.
Также мерой качества программного обеспечения служит связанность модулей программы [6]. Если модули сильно связанны, то программа становится трудномодифицируемой и тяжелой в понимании. Данная мера не выражается численно. Виды связанности модулей:
Связанность по данным — если модули взаимодействуют через передачу параметров и при этом каждый параметр является элементарным информационным объектом. Это наиболее предпочтительный тип связанности (сцепления).
Связанность по структуре данных — если один модуль посылает другому составной информационный объект (структуру) для обмена данными.
Связанность по управлению — если один посылает другому информационный объект — флаг, предназначенный для управления его внутренней логикой.
Модули связаны по общей области в том случае, если они ссылаются на одну и туже область глобальных данных. Связанность (сцепление) по общей области является нежелательным, так как, во-первых, ошибка в модуле, использующем глобальную область, может неожиданно проявиться в любом другом модуле; во-вторых, такие программы трудны для понимания, так как программисту трудно определить какие именно данные используются конкретным модулем.
Связанность по содержимому — если один из модулей ссылается внутрь другого. Это недопустимый тип сцепления, так как полностью противоречит принципу модульности, т.е. представления модуля в виде черного ящика.
Внешняя связанность — два модуля используют внешние данные, например коммуникационный протокол.
Связанность при помощи сообщений — наиболее свободный вид связанности, модули напрямую не связаны друг с другом, о сообщаются через сообщения, не имеющие параметров.
Отсутствие связанности — модули не взаимодействуют между собой.
Подклассовая связанность — отношение между классом-родителем и классом-потомком, причем потомок связан с родителем, а родитель с потомком — нет.
Связанность по времени — два действия сгруппированы в одном модуле лишь потому, что ввиду обстоятельств они происходят в одно время.
Еще одна мера, касающаяся стабильности модуля — мера Колофелло [7], она может быть определена как количество изменений, которые требуется произвести в модулях, отличных от модуля, стабильность которого проверяется, при этом эти изменения должны касаться проверяемого модуля.
1. Для каждой управляющей переменной i вычисляется значениt её сложностной функции C(i) по формуле: C(i) = (D(i) * J(i))/n.
Где D(i) — величина, измеряющая сферу действия переменной i. J(i) — мера сложности взаимодействия модулей через переменную i, n — число отдельных модулей в схеме разбиения.
2. Для всех модулей, входящих в сферу разбиения, определяется значение их сложностных функций M(P) по формуле M(P) = fp * X(P) + gp * Y(P)
где fp и gp — соответственно, число модулей, непосредственно предшествующих и непосредственно следующих за модулем P, X(P) — сложность обращения к модулю P,
Y(P) — сложность управления вызовом из модуля P других модулей.
3. Общая сложность MP иерархической схемы разбиения программы на модули задаётся формулой:
MP = СУММА(M(P)) по всем возможным значениям P — модулям программы.
Данная метрика ориентирована на программы, хорошо структурированные, составленные из иерархических модулей, задающих функциональную спецификацию и структуру управления. Также подразумевается, что в каждом модуле одна точка входа и одна точка выхода, модуль выполняет ровно одну функцию, а вызов модулей осуществляется в соответствии с иерархической системой управления, которая задаёт отношение вызова на множестве модулей программы.
Также существует метрика, основанная на информационной концепции — мера Берлингера [8]. Мера сложности вычисляется как M=СУММАfi*log2pi, где fi — частота появления i-го символа, pi — вероятность его появления.
Недостатком данной метрики является то, что программа, содержащая много уникальных символов, но в малом количестве, будет иметь такую же сложность как программа, содержащая малое количество уникальных символов, но в большом количестве.
5. Объектно-ориентированные метрики
В связи с развитием объектно-ориентированных языков программирования появился новый класс метрик, также называемый объектно-ориентированными метриками. В данной группе наиболее часто используемыми являются наборы метрик Мартина и набор метрик Чидамбера и Кемерера. Для начала рассмотрим первую подгруппу.
Прежде чем начать рассмотрение метрик Мартина необходимо ввести понятие категории классов [9]. В реальности класс может достаточно редко быть повторно использован изолированно от других классов. Практически каждый класс имеет группу классов, с которыми он работает в кооперации, и от которых он не может быть легко отделен. Для повторного использования таких классов необходимо повторно использовать всю группу классов. Такая группа классов сильно связна и называется категорией классов. Для существования категории классов существуют следующие условия:
Классы в пределах категории класса закрыты от любых попыток изменения все вместе. Это означает, что, если один класс должен измениться, все классы в этой категории с большой вероятностью изменятся. Если любой из классов открыт для некоторой разновидности изменений, они все открыты для такой разновидности изменений.
Классы в категории повторно используются только вместе. Они настолько взаимозависимы и не могут быть отделены друг от друга. Таким образом, если делается любая попытка повторного использования одного класса в категории, все другие классы должны повторно использоваться с ним.
Классы в категории разделяют некоторую общую функцию или достигают некоторой общей цели.
Ответственность, независимость и стабильность категории могут быть измерены путем подсчета зависимостей, которые взаимодействуют с этой категорией. Могут быть определены три метрики :
1. Ca: Центростремительное сцепление. Количество классов вне этой категории, которые зависят от классов внутри этой категории.
2. Ce: Центробежное сцепление. Количество классов внутри этой категории, которые зависят от классов вне этой категории.
3. I: Нестабильность: I = Ce / (Ca+Ce). Эта метрика имеет диапазон значений [0,1].
I = 0 указывает максимально стабильную категорию.
I = 1 указывает максимально не стабильную категорию.
Можно определять метрику, которая измеряет абстрактность (если категория абстрактна, то она достаточно гибкая и может быть легко расширена) категории следующим образом:
A: Абстрактность: A = nA / nAll.
Значения этой метрики меняются в диапазоне [0,1].
0 = категория полностью конкретна,
1 = категория полностью абстрактна.
Теперь на основе приведенных метрик Мартина можно построить график, на котором отражена зависимость между абстрактностью и нестабильностью. Если на нем построить прямую, задаваемую формулой I+A=1, то на этой прямой будут лежать категории, имеющие наилучшую сбалансированность между абстрактностью и нестабильностью. Эта прямая называется главной последовательностью.
Далее можно ввести еще 2 метрики:
Расстояние до главной последовательности: D=|(A+I-1)/sqrt(2)|
Нормализированной расстояние до главной последовательности: Dn=|A+I-2|
Практически для любых категорий верно то, что чем ближе они находятся к главной последовательности, тем лучше.
Следующая подгруппа метрик — метрики Чидамбера и Кемерера [10]. Эти метрики основаны на анализе методов класса, дерева наследования и т.д.
WMC (Weighted methods per class), суммарная сложность всех методов класса: WMC=СУММАci, i=1. n, где ci — сложность i-го метода, вычисленная по какой либо из метрик (Холстеда и т.д. в зависимости от интересующего критерия), если у всех методов сложность одинаковая, то WMC=n.
DIT (Depth of Inheritance tree) — глубина дерева наследования (наибольший путь по иерархии классов к данному классу от класса-предка), чем больше, тем лучше, так как при большей глубине увеличивается абстракция данных, уменьшается насыщенность класса методами, однако при достаточно большой глубине сильно возрастает сложность понимания и написания программы.
NOC (Number of children) — количество потомков (непосредственных), чем больше, тем выше абстракция данных.
CBO (Coupling between object classes) — сцепление между классами, показывает количество классов, с которыми связан исходный класс. Для данной метрики справедливы все утверждения, введенные ранее для связанности модулей, то есть при высоком CBO уменьшается абстракция данных и затрудняется повторное использование класса.
RFC (Response for a class) — RFC=|RS|, где RS — ответное множество класса, то есть множество методов, которые могут быть потенциально вызваны методом класса в ответ на данные, полученные объектом класса. То есть RS=((
6. Метрики надежности
Следующий тип метрик — метрики, близкие к количественным, но основанные на количестве ошибок и дефектов в программе. Нет смысла рассматривать особенности каждой из этих метрик, достаточно будет их просто перечислить: количество структурных изменений, произведенных с момента прошлой проверки, количество ошибок, выявленных в ходе просмотра кода, количество ошибок, выявленных при тестировании программы и количество необходимых структурных изменений, необходимых для корректной работы программы. Для больших проектов обычно рассматривают данные показатели в отношении тысячи строк кода, т.е. среднее количество дефектов на тысячу строк кода.
7. Гибридные метрики
В завершении необходимо упомянуть еще один класс метрик, называемых гибридными. Метрики данного класса основываются на более простых метриках и представляют собой их взвешенную сумму. Первым представителем данного класса является метрика Кокола. Она определяется следующим образом:
H_M = (M + R1 * M(M1) +… + Rn * M(Mn)/(1 + R1 +… + Rn)
Где M — базовая метрика, Mi — другие интересные меры, Ri — корректно подобранные коэффициенты, M(Mi) — функции.
Функции M(Mi) и коэффициенты Ri вычисляются с помощью регрессионного анализа или анализа задачи для конкретной программы.
В результате исследований, автор метрики выделил три модели для мер: Маккейба, Холстеда и SLOC, где в качестве базовой используется мера Холстеда. Эти модели получили название «наилучшая», «случайная» и «линейная».
Метрика Зольновского, Симмонса, Тейера также представляет собой взвешенную сумму различных индикаторов. Существуют два варианта данной метрики:
(структура, взаимодействие, объем, данные) СУММА(a, b, c, d).
(сложность интерфейса, вычислительная сложность, сложность ввода/вывода, читабельность) СУММА(x, y, z, p).
Используемые метрики в каждом варианте выбираются в зависимости от конкретной задачи, коэффициенты — в зависимости от значения метрики для принятия решения в данном случае.