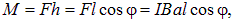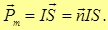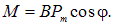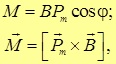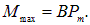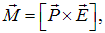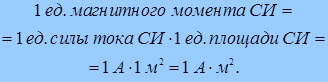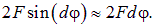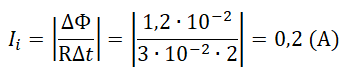вращение контура в магнитном поле

5.7. Контур с током в магнитном поле

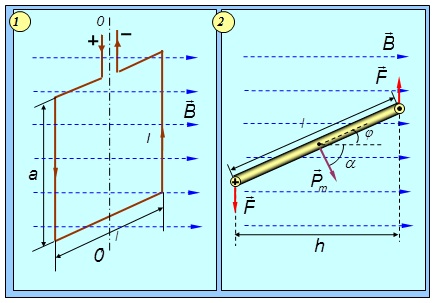
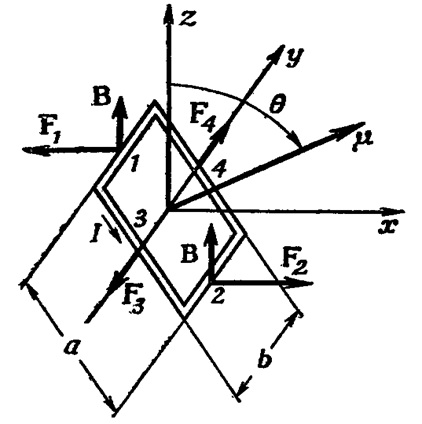
Пусть контур с током помещен в магнитное поле, причем он может вращаться вокруг вертикальной оси OO’ (рис. 5.30-1). Силы Ампера, действующие на стороны контура длиной l, перпендикулярны к ним и к магнитному полю и поэтому направлены вертикально: они лишь деформируют контур, стремясь растянуть его. Стороны, имеющие длину a, перпендикулярны B, так что на каждую из них действует сила F = BIa. Эти силы стремятся повернуть контур таким образом, чтобы его плоскость стала ортогональной B.

Рис. 5.30. Силы, действующие на контур с током в магнитном поле:
1 — вид сбоку; 2 — вид сверху (масштаб увеличен)

Видео 5.7. Контур с током в однородном магнитном поле.

Момент пары сил (рис. 5.30-2) равен

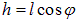
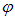
где — плечо пары сил, а — угол между вектором B и стороной l.

Величина, численно равная произведению силы тока I, протекающего в контуре, на площадь контура S = al называется магнитным моментом P_m плоского контура стоком

Таким образом, мы можем записать момент пары сил в виде

Магнитный момент контура с током — векторная величина. Направление Р_m совпадает с положительным направлением нормали к плоскости контура, которое определяется правилом винта: если рукоятка вращается по направлению тока в контуре, то поступательное движение винта показывает направление вектора P_m . Введем в формулу (15.36) угол a между векторами P_m и B. Справедливо соотношение

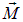
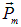
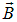
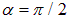
то есть момент сил , действующий на виток с током в однородном магнитном поле, равен векторному произведению магнитного момента витка на вектор индукции магнитного поля (рис. 5.31). При величина момента сил максимальна

Рис. 5.31. Силы, действующие на прямоугольный контур с током в магнитном поле.
Магнитное поле вертикально, а магнитный момент перпендикулярен плоскости контура

Опять-таки прозрачна аналогия с электростатикой: говоря об электрическом диполе, мы получили выражение для момента сил, действующих на него со стороны электрического поля в виде

где 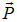— электрический дипольный момент.

В системе СИ единицей измерения магнитного момента контура является ампер на квадратный метр (А · м 2 )

Видео 5.10. «Сознательные катушки»: отталкивание и притяжение параллельных токов и поворот магнитного момента по магнитному полю.

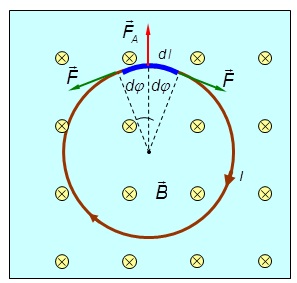
Пример. По тонкому проводу в виде кольца радиусом 30 см течет ток 100 A. Перпендикулярно плоскости кольца возбуждено однородное магнитное поле с магнитной индукцией 20 мТл (рис. 5.32). Найти силу, растягивающую кольцо.

Рис. 5.32. Силы, растягивающие кольцо с током в магнитном поле

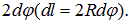
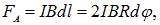
Решение. Пусть магнитное поле направлено от нас за плоскость рис. 5.32 (показано крестиками), а ток идет по часовой стрелке. Выделим элемент длины dl, видный из центра под углом На этот элемент действует сила Ампера направленная по радиусу кольца. Кроме того, из-за растяжения кольца на концы элемента действуют силы натяжения F, которые и требуется найти в задаче. Проекция этих сила на радиальное направление равна

Приравнивая эту проекцию силе Ампера, находим

Источник

Вращение контура в магнитном поле

Пусть в однородное магнитное поле помещена рамка с током (рис. 4.13). Тогда силы Ампера, действующие на боковые стороны рамки, будут создавать вращающий момент, величина которого пропорциональна магнитной индукции, силе тока в рамке, ее площади S и зависит от угла a между вектором и нормалью к площади :

Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке.

Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:

Это выражение также можно использовать для определения индукции магнитного поля:

Величину, равную произведению , называют магнитным моментом контура Р_т. Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Тогда вращательный момент можно записать

При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.

Источник

Вращение контура в магнитном поле

ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

§1 Явление электромагнитной индукции.

Закон Фарадея

а) В соленоид, замкнутый на гальванометр, вдвигается и выдвигается постоянный магнит. На гальванометре будет отклонение стрелки, и оно будет тем больше, чем быстрее происходит вдвижение и выдвижение. При изменении полюсов магнита направление отклонения стрелки изменится.

б) В соленоид, замкнутый на гальванометр, вставлена катушка (другой соленоид), через которую пропускается ток. При включении и выключении (т.е. при любом изменении тока) происходит отклонение стрелки гальванометра. Направление отклонения изменяется при включении – выключении, уменьшении – увеличении тока, вдвигании – выдвигании катушек.

Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает индукционный (наведенный) электрический ток.

В 1834 г. Э.Х. Ленц установил закон, позволяющий определить направление индукционного тока.

Правило Ленца : индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.

Знак минус в законе Фарадея является математическим выражением правила Ленца.

— потокосцепление или полный магнитный поток.

Т.к. Ф _B = BScosα , то для того чтобы изменить магнитный поток Ф можно изменить:

1) магнитное поле ;

§2 Вращение рамки в магнитном поле

Явление электромагнитной индукции используется для преобразования механической энергии и энергии электрического тока в генераторах.

Рамка площадью S вращается в однородном магнитном поле ( ) равномерно с постоянной угловой скоростью ω.

Если через рамку, помещенную в магнитном поле, пропускать электрический ток, то на нее будет действовать вращающий момент

и рамка начнет вращаться. На этом принципе основана работа электродвигателей, предназначенных для превращения электрической энергии в механическую.

§3 Токи Фуко.

Индукционные токи могут возбуждаться и в сплошных массивных проводниках. В этом случае их называют токами Фуко или вихревыми токами. Электрическое сопротивление массивного проводника мало, поэтому токи Фуко могут достигать очень большой силы.

Токи Фуко, как и индукционные токи в линейных проводниках, подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать изменению магнитного поля, индуцирующего вихревые токи. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Это используют для демпфирования (успокоения) подвижных частей гальванометров, сейсмографов и т.п. Тепловое действие токов Фуко используется в индукционных плавильных печах.

Для уменьшения токов Фуко сердечники трансформаторов делают из отдельных пластин и пластины перпендикулярны токам Фуко.

§4 Индуктивность контура.

Самоиндукция

В любом случае, когда по контуру протекает электрический ток, создается магнитное поле. При этом всегда имеется магнитный поток Ф, проходящий через поверхность, ограниченную рассматриваемым контуром. Любое изменение силы тока в контуре приводит к изменению магнитного поля, сцепленного с контуром, а это в свою очередь вызывает появление индукционного тока. Это явление получило название явления самоиндукции: возникновение Э ДС индукции в проводнике при изменении в нем тока.

Из закона Био-Савара-Лапласа следует

т.е. магнитный поток, сцепленный с контуром, пропорционален току I в контуре

Рассчитаем индуктивность L соленоида:

магнитная индукция В соленоида

т.е. индуктивность зависит от геометрических размеров соленоида ( ), числа витков и магнитной проницаемости сердечника соленоида. Поэтому можно сказать, что индуктивность L аналог емкости С уединенного проводника, которая также зависит от геометрических размеров, от формы и диэлектрической проницаемости среды.

Применяя к явлению самоиндукции закон Фарадея, получим, что Э ДС самоиндукции

где знак минус, обусловленный правилом Ленца, показывает, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем. Если ток со временем возрастает, то , и т.е. ток самоиндукции направлен навстречу току, обусловленному внешним источником и тормозит его возрастание. Если ток со временем убывает, то и т.е. индукционный ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание. Следовательно, контур, обладающий индуктивностью, имеет электрическую инертность, заключающуюся в том, что любое изменение тока тормозится, тем сильнее, чем больше индуктивность контура.

Источник

Закон электромагнитной индукции

теория по физике 🧲 магнетизм

Магнитный поток наглядно истолковывается как число линий магнитной индукции, пронизывающих поверхность площадью S. Поэтому скорость изменения этого числа есть не что иное, как скорость изменения магнитного потока.

Сила индукционного тока пропорциональная скорости изменения магнитного потока через поверхность, ограниченную контуром:

Согласно закону Ома для замкнутой цепи:

Сопротивление проводника не зависит от изменения магнитного потока. Следовательно, сила индукционного тока пропорциональна скорости изменения магнитного потока только потому, что ЭДС индукции тоже пропорциональна этой скорости изменения потока.

Закон электромагнитной индукции

ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.

Закон электромагнитной индукции формулируется именно для ЭДС, а не для силы тока. При такой формулировке закон выражает сущность явления, не зависящую от свойств проводников, в которых возникает индукционный ток.

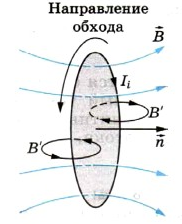
Определение знака ЭДС индукции

На рисунке изображен замкнутый контур. Будем считать положительным направление обхода контура против часовой стрелки. Нормаль → n к контуру образует правый винт с направлением обхода.

Пример №1. Магнитный поток через контур проводника сопротивлением 3∙10 –2 Ом за 2 с изменился на 1,2∙10 –2 Вб. Найдите силу тока в проводнике, если изменение потока происходило равномерно.

ЭДС индукции в движущихся проводниках

Электроны в неподвижном проводнике приводятся в движение электрическим полем, и это поле порождается переменным магнитным полем. Следовательно, изменяясь во времени, магнитное поле порождает электрическое поле. Но если проводник движется в постоянном во времени магнитном поле, то ЭДС индукции в проводнике обусловлена не вихревым электрическим полем, которое в этом случае не может возникнуть, а другой причиной.

При движении проводника его свободные заряды движутся вместе с ним. Поэтому на заряды со стороны магнитного поля действует сила Лоренца. Она и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет магнитное происхождение.

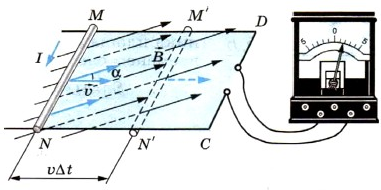
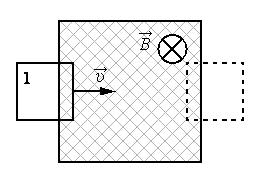
Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле (см. рисунок). Пусть сторона контура MN длиной l скользит с постоянной скоростью → v вдоль сторон NC и MD, оставаясь все это время параллельной стороне CD. Вектор магнитной индукции → B однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.

Сила, с которой магнитное поле действует на движущуюся заряженную частицу, равна по модулю:

Направлена эта сила вдоль проводника MN. Работа силы Лоренца на пути l положительна и составляет:

Формула выше определяет неполную работу силы Лоренца. Кроме силы Лоренца имеется составляющая силы Лоренца, направленная против скорости проводника → v . Такая составляющая тормозит проводник и совершает отрицательную работу. В результате полная работа силы Лоренца оказывается равной нулю.

Электродвижущая сила индукции в проводнике MN равна по определению отношению работы по перемещению заряда q к этому заряду:

Эта формула справедлива для любого проводника длиной l, движущегося со скоростью → v в однородном магнитном поле.

В других проводниках контура ЭДС равна нулю, так как проводники неподвижны. Следовательно, ЭДС во всем контуре MNCD равна ε i и остается неизменной, если скорость движения → v постоянна. Электрический ток при этом будет увеличиваться, так как при смещении проводника MN вправо уменьшается общее сопротивление контура.

С другой стороны, ЭДС индукции можно вычислить с помощью закона электромагнитной индукции. Магнитный поток через контур MNCD равен:

угол 90 ° − α представляет собой угол между векторами → B и нормалью → n к поверхности контура, а S — площадь контура MNCD. Если считать, что в начальный момент времени t=0 проводник MN находится на расстоянии NC от проводника CD, то при перемещении проводника площадь S изменяется со временем следующим образом:

Пример №2. Проводник длиной 50 см движется в однородном магнитном поле со скоростью 4 м/с перпендикулярно силовым линиям. Найдите разность потенциалов, возникающую на концах проводника, если вектор магнитной индукции 8 мТл.

Так как проводник движется перпендикулярно силовым линиям, то угол α равен 90 градусам, а синус прямого угла равен единице. Поэтому:

В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R=10Ом и стороной l=10см перемещают в плоскости рисунка поступательно со скоростью υ=1м/с. Чему равен индукционный ток в рамке в состоянии 1?

Источник

Вращение контура в магнитном поле

Величина силы вычисляется по формуле:

Направление силы определяют в соответствии с векторным произведением либо используя правило левой руки : если расположить левую руку так, чтобы вектор магнитной индукции входил бы в ладонь, а четыре сложенных пальца были направлены вдоль тока, то отогнутый большой палец покажет направление действия силы.

Рис. 3.7.2. Сила взаимодействия между прямолинейными проводниками

Выражение (3.7.3) совпадает с ранее введенным (3.6.1). Для силы f₁₂, действующей на единицу длины тока i₁, получается аналогичное соотношение. С помощью правила левой руки легко установить, что при одинаковом направлении токов они притягивают друг друга и отталкиваются при противоположном направлении.

3.7.2. Сила Лоренца

Проводник, по которому течет ток, отличается от проводника без тока только тем, что в нем происходит упорядоченное движение зарядов. Отсюда следует, что сила, действующая на проводник с током в магнитном поле, обусловлена действием сил на отдельные движущиеся заряды, и от них передается проводнику.

Для объемной плотности этой силы имеем:

Используя выражение для плотности тока, (3.7.5) можно переписать так:

Рис. 3.7.3. Направление силы Лоренца

Поскольку сила Лоренца всегда направлена перпендикулярно скорости заряженной частицы, она не совершает работы над частицей. Следовательно, действуя на заряженную частицу постоянным магнитным полем, нельзя изменить ее энергию.

3.7.3. Контур с током в магнитном поле

Пусть прямоугольный плоский контур с током помещается в однородном магнитном поле. Если контур ориентирован так, что вектор магнитной индукции параллелен его плоскости (Рис. 3.7.4), то стороны, имеющие длину b, не будут испытывать действие силы Ампера, так как для этих сторон sinα = 0.

Рис. 3.7.4. Контур с током в постоянном магнитном поле

Учитывая, что ab = S (площади контура), а произведение iS = p_m, соотношение (3.7.9) можно представить так:

что совпадает с определением (3.6.3).

Рис. 3.7.5.Равновесная ориентация контура с током в магнитном поле

В этом случае выполняется:

Направления всех сил (3.7.11) лежат в плоскости контура. Вращательный момент в этом случае не возникает. Равнодействующая всех сил равна нулю; силы лишь растягивают контур, не перемещая и не поворачивая его в пространстве. Если повернуть контур на 180° или изменить направление магнитного поля на противоположное, то направления всех сил изменятся на противоположные, и они будут сжимать контур.

Рис. 3.7.6. Случай произвольной ориентации контура с током в магнитном поле

Для того, чтобы угол α между векторами и увеличить на dα, нужно совершить против сил, действующих на контур с током в магнитном поле, работу:

Поворачиваясь в первоначальное положение, контур может возвратить затраченную на его поворот работу, совершив ее над какими-либо телами. Следовательно, работа (3.7.14) идет на увеличение энергии W, которую получает контур с током в магнитном поле:

Интегрируя (3.7.15), можно получить:

Полагая const = 0, получаем формулу для энергии контура с током в магнитном поле:

Вообще, поворот контура с током в магнитном поле положен в основу действия электрических двигателей.

3.7.4. Работа, совершаемая при перемещении
проводника с током в магнитном поле

Пусть проводник с током может свободно перемещаться во внешнем магнитном поле. Это можно осуществить с помощью скользящих контактов между концами провода и остальными участками замкнутой цепи (Рис. 3.7.7).

Рис. 3.7.7. К расчету работы при перемещении тока в магнитном поле

Однородное внешнее поле перпендикулярно плоскости контура. Тогда сила будет направлена вправо и равна:

На пути ds эта сила совершит над проводником работу:

Рассмотрим магнитное поле в соленоиде. Соленоидом называют катушку цилиндрической формы из провода, витки которого намотаны в одном направлении (Рис. 3.7.8).

Рис. 3.7.8. Магнитное поле в соленоиде

Пусть соленоид (Рис. 3.7.9) имеет длину l, радиус его витков равен R, число витков составляет N, сила тока равна I.

Рис. 3.7.9. К расчету магнитного поля в соленоиде

Рассматривая соленоид как совокупность вплотную прилегающих витков (круговых токов I), имеющих общую ось, определим индукцию магнитного поля В в точке А на оси соленоида как сумму индукций каждого из витков. Воспользуемся формулой (3.6.14), которую сейчас следует записать так:

Выделим участок соленоида длиной dr₀. В нем содержится Ndr₀/l витков. Тогда индукция поля от одного витка равна:

Интегрируя (3.7.22) в пределах от α = α₁ до α = α₂, найдем полную индукцию:

Для бесконечно длинного соленоида выполняется α₁ = 0° и α₂ = 180°. Поэтому получим:

Если соленоид заполнен магнитным материалом с магнитной проницаемостью μ, то (3.7.23) должно быть записано так:

Отметим, что работа совершается не за счет магнитного поля (сила Лоренца работы над движущимися зарядами не совершает), а за счет источника, поддерживающего ток в контуре.

© ФГОУ ВПО Красноярский государственный аграрный университет, 2015

Источник