вся программа 7 класса по алгебре учение
Вся программа 7 класса по алгебре учение
Выражения и их преобразования
☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а: 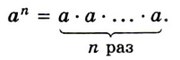
Степень числа а ≠ 0 с показателем 0 равна 1: а 0 = 1.
☑ 2. Свойства степеней с натуральными показателями:
а m • а n = а m+n
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
(а m ) n = а mn
При возведении степени в степень основание оставляют прежним, а показатели перемножают.
(ab) n = а n b n
При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.
Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а 2 b 4 равна 6.
☑ 4. Многочленом называют сумму одночленов. Например, 3х 5 – 4х 2 + 1, 7a 3 b – ab 2 + ab + 6 —многочлены. Одночлены считают многочленами, состоящими из одного члена.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х 3 у + 3х 2 у 5 + ху равна степени одночлена 3х 2 у 5 , т. е. равна 7.
Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
☑ 5. При сложении многочленов пользуются правилом раскрытия скобок : если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,
(3аb + 5с 2 ) + (ab – с 2 ) = 3ab + 5с 2 + ab – с 2 = 4аb + 4с 2
При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,
(6x 2 – у) – (2x 2 – 8у) = 6х 2 – у – 2х 2 + 8у = 4х 2 + 7у
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,
а 2 (3аb – b 3 + 1) = 3а 3 b – а 2 b 3 + а 2
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,
(5х – 1)(3х + 2) = 15x 2 – Зx + 10x – 2 = 15x 2 + 7x – 2
☑ 6. Формулы сокращённого умножения:
(а + b) 2 = а 2 + 2аb + b 2
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а – b) 2 = а 2 – 2аb + b 2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а + b) 3 = а 3 + 3а 2 b + 3ab 2 + b 3
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(а – b) 3 = а 3 – 3а 2 b + Заb 2 – b 3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(а – b)(а + b) = а 2 – b 2
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
а 3 + b 3 = (а + b)(a 2 – аb + b 2 )
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
а 3 – b 3 = (а – b)(a 2 + ab + b 2 )
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.
Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х 3 – х 2 у можно разложить на множители, вынеся за скобки х 2 :
Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:
3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).
Многочлен а 4 – 25x 2 можно разложить на множители, используя формулу разности квадратов двух выражений:
а 4 – 25x 2 = (а 2 ) 2 – (5x) 2 = (а 2 – 5x)(а 2 + 5x).
Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.
Алгебра 7 класс Все формулы
Уравнения
Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.
☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x 2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.
При решении уравнений с одной переменной используются следующие свойства:
Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.
Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.
Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.
В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.
☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.
☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы 
Решить систему уравнений — значит найти все её решения или доказать, что решений нет.
Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.
☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.
При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:
При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:
При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:
Алгебра 7 класс Все формулы
Функции
Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.
Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.
Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.
График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k у = х 2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.
График функции у = х 3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.
Статистические характеристики
☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.
Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.
Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.
Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.
Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.
Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.
Вы смотрели Конспект «Алгебра 7 класс Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:
Рабочая программа 7 класс Алгебра
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«Средняя общеобразовательная школа №61» г. Брянска
Рассмотрено на заседании МО учителей математики, физики, информатики
Протокол № 1 от «27»августа 2018 г.
Заместитель директора школы по УВР МБОУ СОШ №61
Директор МБОУ СОШ №61
_____________ Синявина В.С.
от «30» августа 2018 г.
учебного предмета «Математика»
на 2019-2029 учебный год.
Громова Ирина Владимировна,
1. Планируемые результаты освоения учебного предмета.
Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:
сформированность ответственного отношения к учению, готовность и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов;
сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими, в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативность мышления, инициатива, находчивость, активность при решении алгебраических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;
умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности ее решения;
осознанное владение логическими действиям и определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родо-видовых связей;
умение устанавливать причинно-следственные связи; строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций ролей участников, взаимодействие и общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; слушать партнера; формулировать, аргументировать и отстаивать свое мнение;
сформированность учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ – компетентности);
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения;
владение базовым понятийным аппаратом: иметь представление о числе, владение символьным языком алгебры, знание элементарных функциональных зависимостей, формирование представлений о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
умение выполнять алгебраические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;
умение пользоваться математическими формулами и самостоятельно составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента;
умение решать линейные уравнения и неравенства, а также приводимые к ним уравнения, неравенства, системы; применять графические представления для решения и исследования уравнений, неравенств, систем; применять полученные умения для решения задач из математики, смежных предметов, практики;
овладение системой функциональных понятий, функциональным языком и символикой, умение строить графики функций, описывать их свойства, использовать функционально-графические представления для описания и анализа математических задач и реальных зависимостей;
овладение основными способами представления и анализа статистических данных;
умение применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
2. Содержание учебного предмета
Алгебраические выражения. Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных. Подстановка выражений вместо переменных. Преобразование буквенных выражений на основе свойств арифметических действий. Равенство буквенных выражений. Тождество.
Степень с натуральным показателем и ее свойства. Одночлены и многочлены. Степень многочлена. Сложение, вычитание, умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности, куб суммы и куб разности. Формула разности квадратов, формулы суммы кубов и разности кубов. Разложение многочлена на множители
Уравнения и неравенства. Уравнение с одной переменной. Корень уравнения. Линейное уравнение.
Уравнение с двумя переменными; решение уравнения с двумя переменными. Система уравнений; решение системы. Система двух линейных уравнений с двумя переменными; решение подстановкой и алгебраическим сложением.
Переход от словесной формулировки соотношений между величинами к алгебраической. Решение текстовых задач алгебраическим способом.
Числовые функции. Функции, описывающие прямую и обратную пропорциональную зависимости, их графики. Линейная функция, ее график, геометрический смысл коэффициентов. Использование графиков функций для решения уравнений и систем.
Множества и комбинаторика. Примеры решения комбинаторных задач: перебор вариантов, правило умножения.
Статистические данные. Представление данных в виде таблиц, диаграмм, графиков. Средние результатов измерений. Понятие о статистическом выводе на основе выборки.
Рабочая программа по алгебре в 7 классе

Рассмотрена на заседании ШМО, Принята на заседании Утверждена протокол №1 от 30.08.2021г. педагогического совета, приказом директора школы Руководитель ШМО: протокол №1 от 30.08.2021г. №93 от 31.08.2021г.
_______ Т.Г. Пестрецова Председатель ПС: ________ _______Н.Г. Картамышева
Класс: 7
Количество часов:102
Уровень: базовый
Срок реализации: 1 год
Учитель: Пестрецова Татьяна Георгиевна
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ УЧЕБНОГО ПРЕДМЕТА
У ученика сформируется:
— нормы поведения в рамках межличностных отношений,
— ориентация в нравственном содержании и смысле поступков как собственных, так и окружающих людей;
— основы гражданской идентичности личности в форме осознания «Я» как гражданина России, чувства сопричастности и гордости за свою Родину, народ и историю, осознание ответственности человека за общее благополучие, осознание своей этнической принадлежности;
— социальные нормы, правила поведения, роли и формы социальной жизни в группах и сообществах, включая взрослые и социальные сообщества;
— основы социально-критического мышления.
Ученик получит возможность для формирования:
— морального сознания на конвенциональном уровне;
— способности к решению моральных дилемм на основе учета позиций партнеров в общении, ориентации на их мотивы и чувства, устойчивое следование в поведении моральным нормам и этическим требованиям.
Регулятивные УУД
Ученик научится:
— оценивать правильность выполнения действия на уровне
адекватной ретроспективной оценки;
— осуществлять итоговый и пошаговый контроль по результату.
Ученик получит возможность научиться:
— осуществлять констатирующий и предвосхищающий контроль по результату и по способу действия, актуальный контроль на уровне произвольного внимания.
— допускать возможность существования у людей различных
точек зрения, в том числе не совпадающих с его собственной, и ориентироваться на позицию партнера в общении и взаимодействии;
— договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов.
Ученик получит возможность научиться:
— действовать с учетом позиции другого и уметь согласовывать свои действия;
— устанавливать и поддерживать необходимые контакты с другими людьми, владея нормами и техникой общения.
— осуществлять анализ объектов с выделением существенных
и несущественных признаков;
— осуществлять синтез как составление целого из частей;
— проводить сравнение и классификацию по заданным критериям.
Ученик получит возможность научиться:
— осуществлять синтез как составление целого из частей,
самостоятельно достраивая и восполняя недостающие
— осуществлять сравнение и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций.
— понимать особенности десятичной системы счисления;
— владеть понятиями, связанными с делимостью натуральных чисел;
— выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;
— сравнивать и упорядочивать рациональные числа;
— выполнять вычисления с рациональными числами, сочетая устные и письменные приемы вычислений, применение калькулятора;
— использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчеты.
Ученик получит возможность:
— познакомиться с позиционными системами счисления с основаниями, отличными от 10;
— углубить и развить представления о натуральных числах и свойствах делимости;
— научится использовать приемы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.
— владеть понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные; работать с формулами;
— выполнять преобразования выражений, содержащих степени с натуральным показателем;
— выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами;
— выполнять разложение многочленов на множители.
Ученик получит возможность:
— научится выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приемов;
— применять тождественные преобразования для решения задач из различных разделов курса.
— решать линейные уравнения с одной переменной, системы двух уравнений с двумя переменными;
— понимать уравнение как важную математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
— применять графические представления для исследования уравнений, исследование и решение систем уравнений с двумя переменными.
Ученик получит возможность:
— овладеть специальными приемами решения уравнений и систем уравнений; уверенно применять аппарат уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
— применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
ОСНОВНЫЕ ПОНЯТИЯ. ЧИСЛОВЫЕ ФУНКЦИИ
— понимать и использовать функциональные понятия и язык (термины, символические обозначения);
— строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;
— понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.
Ученик получит возможность научиться:
— проводить исследования, связанные с изучением свойств функции, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т.п.);
— использовать функциональные представления и свойства функций для решения математических задач из различных разделов.
СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА
Глава 1. Выражения, тождества, уравнения (22 ч)
Числовые выражения и выражения с переменными. Простейшие преобразования выражений. Уравнение с одним неизвестным и его корень, линейное уравнение. Решение задач методом уравнений.
Функция, область определения функции, Способы задания функции. График функции. Функция y = kx + b и её график. Функция y = kx и её график.
Глава 3. Степень с натуральным показателем (14 ч)
Степень с натуральным показателем и её свойства. Одночлен. Функции y = x 2 , y = x 3 , и их графики.
Глава 4. Многочлены (15 ч)
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочлена на множители.
Глава 5. Формулы сокращённого умножения (18 ч)
Формулы 
6. Системы линейных уравнений (11 ч)
Система уравнений с двумя переменными. Решение систем двух линейных уравнений с двумя переменными. Решение задач методом составления систем уравнений..
Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 7 класса)

