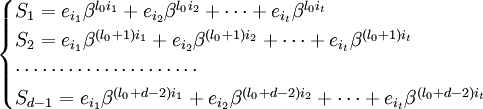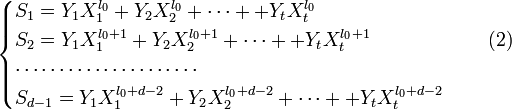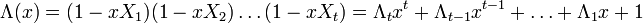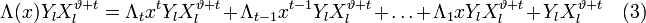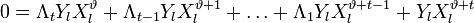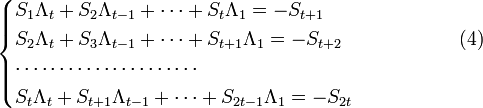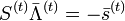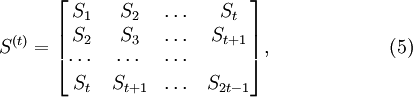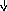вычисление синдрома бчх кода

Код БЧХ

Коды Боуза — Чоудхури — Хоквингхема (БЧХ-коды) — в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с заранее определенными корректирующими свойствами, а именно, минимальным кодовым расстоянием. Коды Рида — Соломона являются частным случаем БЧХ-кодов.

Содержание

Формальное описание

БЧХ-код является циклическим кодом, который можно задать порождающим полиномом. Для его нахождения в случае БЧХ-кода необходимо заранее определить длину кода n (она не может быть произвольной) и требуемое минимальное расстояние 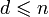. Найти порождающий полином можно следующим образом.

Построение

Для нахождения порождающего полинома необходимо выполнить несколько этапов:

Примеры кодов

Примитивный 2-ичный (15,7,5) код

16-ричный (15,11,5) код (код Рида — Соломона)

g(x) = (x − α)(x − α 2 )(x − α 3 )(x − α 4 ) = x 4 + α 13 x 3 + α 6 x 2 + α 3 x + α 10

Каждому элементу поля GF(16) можно сопоставить 4 битам, поэтому одно кодовое слово эквивалентно 60=15*4 битам, таким образом набору из 44 бит ставится в соответствие набор из 60 бит. Можно сказать, что такой код работает с полубайтами информации.

Кодирование

Для кодирования кодами БЧХ применяются те же методы, что и для кодирования циклическими кодами.

Методы декодирования

Коды БЧХ являются циклическими кодами, поэтому к ним применимы все методы, используемые для декодирования циклических кодов. Однако существуют гораздо лучшие алгоритмы, разработанные именно для БЧХ-кодов.

Алгоритм Питерсона — Горенстейна — Цирлера (ПГЦ)

.

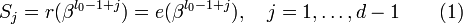
Составим полином локаторов ошибок:

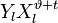
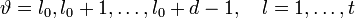
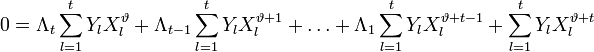
Корнями этого полинома являются элементы, обратные локаторам ошибок. Помножим обе части этого полинома на . Полученное равенство будет справедливо для :

.

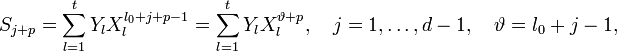
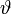
Учитывая (2) и то, что (то есть меняется в тех же пределах, что и ранее) получаем систему линейных уравнений:

Или в матричной форме

См. также

Литература

Полезное

Смотреть что такое «Код БЧХ» в других словарях:

Код Боуза — Чоудхури — Хоквингема — Коды Боуза Чоудхури Хоквингхема (БЧХ коды) в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с… … Википедия

КОД С ИСПРАВЛЕНИЕМ ОШИБОК — код, корректирующий ошибки, множество сообщений, предназначенных для передачи по каналу связи с шумами, обладающее тем свойством, что окрестность ошибок каждого сообщения (т. е. совокупность искаженных вариантов этого сообщения) не пересекается с … Математическая энциклопедия

Код Рида — Соломона — Коды Рида Соломона недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код… … Википедия

БЧХ код — код Боуза Чоудхури Хоквенгема Семейство циклических двоичных кодов с исправлением ошибок. Длина кода n, определяется как 2n t, где t — пюбое целое положительное число (t > 3). Такой код позволяет исправлять t ошибок, при этом длина кода… … Справочник технического переводчика

код Бозе-Чаудхури-Хоккеигема — БЧХ код — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы БЧХ код EN Bose Chaudhuiri Hocquehgam (ВСН) code … Справочник технического переводчика

КОД С ИСПРАВЛЕНИЕМ АРИФМЕТИЧЕСКИХ ОШИБОК — код, исправляющий арифметические ошибки, код, предназначенный для контроля работы сумматора. При сложении чисел, представленных в двоичной системе счисления, одиночный сбой в работе сумматора приводит, как правило, к изменению результата на нек… … Математическая энциклопедия

Код Боуза — Коды Боуза Чоудхури Хоквингхема (БЧХ коды) в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с… … Википедия

Код Боуза-Чоудхури-Хоквингема — Коды Боуза Чоудхури Хоквингхема (БЧХ коды) в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с заранее… … Википедия

Код коррекции ошибок Рида-Соломона — Коды Рида Соломона недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код… … Википедия

Код Рида-Соломона — Коды Рида Соломона недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код… … Википедия

Источник

Вычисление синдрома и исправление ошибок в циклических кодах

Вычисление синдрома для циклических кодов является довольно простой процедурой.

Пусть U(x) и r(х) ‑ полиномы, соответствующие переданному кодовому слову и принятой последовательности.

Если r(x) является кодовым полиномом, то он делится на g(x) без остатка, то есть s(x) = 0.

Следовательно, s(x)  0 является условием наличия ошибки в принятой последовательности, то есть синдромом принятой последовательности.

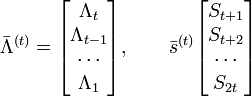
Синдром s(x) имеет в общем случае вид

При наличии в принятой последовательности r хотя бы одной ошибки вектор синдрома S будет иметь, по крайней мере, один нулевой элемент, при этом факт наличия ошибки легко обнаружить

Покажем, что синдромный многочлен S(x) однозначно связан с многочленом ошибки e(x), а значит, с его помощью можно не только обнаруживать, но и локализовать ошибку в принятой последовательности.

— полином вектора ошибки.

Тогда полином принятой последовательности

Прибавим в этом выражении слева и справа U(x), а также учтем, что

, (27)

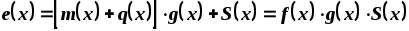
то есть синдромный полином S(x) есть остаток от деления полинома ошибки e(x) на порождающий полином g(x).

Отсюда следует, что по синдрому S(x) можно однозначно определить вектор ошибки e(x), а следовательно, исправить эту ошибку.

По кодирующему многочлену x 7 + x 5 + x + 1 построить полиномиальные коды для двоичных сообщений 0100, 10001101, 11110.

Принадлежат ли коду Голея кодовые слова 10000101011111010011111 и 11000111011110010011111?

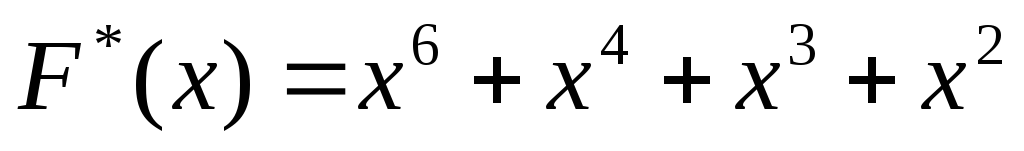
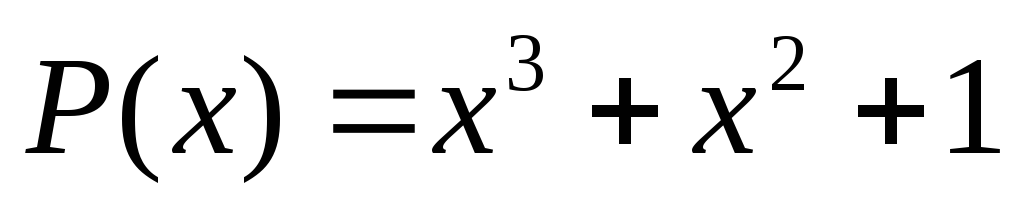
Получено сообщение циклическим кодом . Проверить декодированием наличие ошибок в принятой комбинации, если образующий полином .

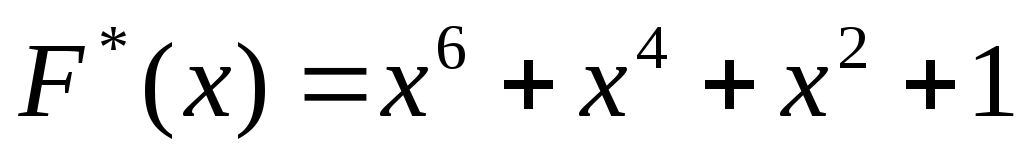
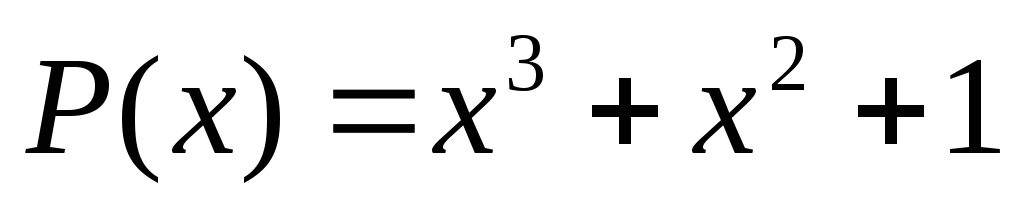
Получена комбинация , закодированная циклическим кодом. Образующий полином . Проверить наличие ошибок в кодовой комбинации.

Лабораторная работа № 11

Коды Боуза- Чоудхури – Хоккенгема

1. Порядок выполнения работы

1.1.Ознакомится с методическими указаниями, изложенными в п.3;

1.2.Выполнить задания (по указанию преподавателя)

2. Содержание отчета:

2.1.Тема и цель работы

2.4.Выводы по работе.

3.Общие сведения

Французский ученый А. Хоквингем (1959 г.) и американцы Р. К. Боуз и Д. К. Рой-Чоудхури (1960 г.) нашли большой класс кодов, обеспечивающий произвольное минимальное кодовое расстояние dmin ≥ 5. Они получили название БЧХ (Боуза-Чоудхури-Хоквингема). Порождающие полиномы для таких кодов в зависимости от предъявляемых к ним требований, можно найти в таблице

Где n — общее число элементов, m — число информационных элементов, k — число избыточных элементов (n = m + k).

Процедура построения кода БЧХ по заданным M и dmin:

по d_min найти значение, при котором обеспечивается необходимое число информационных элементов m при минимальной избыточности k_min;

найти в таблице соответствующий порождающий полином;

если d_min четное, умножить найденный полином на (x + 1);

если m_табл >> m_задан, то можно перейти к укороченному циклическому коду, вычеркивая в порождающей матрице исходного кода с параметрами m_табл, k_min (m_табл − m_задан) столбцов слева и столько же строк сверху.

Методика построения БЧХ. Методика построения кодов БЧХ аналогична общей методике построения ц. к. и отличается в основном выбором образующего многочлена.

Последовательность построения P(x) для кодов БЧХ тоже, что и для обычных ц.к., однако образующий полином является произведением t неприводимых полиномов,

Методика выбора (построения) образующего полинома основана на понятии корня двоичного многочлена и теоремы БЧХ.

Понятие корня двоичного многочлена.

Элемент является корнем двоичного полинома f(x), если f()=0.

Количество корней многочлена равно степени полинома.

Пример 1: f(x)=(x+1) – количество корней – 1; _

Пример 2: Пусть требуется определить все корни бинома x 15 +1.

Представление x 15 +1 в виде произведения неприводимых сомножителей:

x 15 +1 = (x+1)(x 2 +x+1)(x 4 +x+1)(x 4 +x 3 +1)(x 4 +x 3 +x 2 +x+1).

Корни полинома получены Питерсеном и сведены в специальную таблицу.

f₅(x): x 4 +x 3 +x 2 +x+1

Т.е. каждый корень _i является корнем f_j(x) и корнем порождающего бинома x 15 +1 и имеет свой порядковый номер.

Для построения полинома кодов БЧХ используется теорема БЧХ: (без доказательств)

Если образующий полином содержит непрерывную цепь из m корней, то данный порождающий полином обладает корректирующими свойствами кода с d_min=m+1.

При этом ц.к., исправляющие одиночные ошибки являются частным случаем (m=2) из общей теоремы БЧХ.

Пример: 1). Если взять в качестве порождающего

f₃(x) _, __, _{}m=2

f₄(x): _, __, _ m=2

2). F=f₃(x)*f₅(x) _, _₄, _, ₇, _₁₀, _3 m=4 d_min5.

Поскольку (как уже было отмечено выше) методика этапов кодирования и декодирования кодов БЧХ отличается от кодов, исправляющих одиночные ошибки, только выбором образующего многочлена, рассмотрим методику выбора P(x) для БЧХ.

Методика выбора порождающего полинома для кодов БЧХ.

Определение количества информационных разрядов:

Определение количества проверочных разрядов:

n = k + r = k + t _* h  2 h – 1;

t – кратность ошибки.

Длины кодовой комбинации n = k + r и степени бинома x n + 1.

3. Разложение (представление) x n + 1 в виде произведения неприводимых сомножителей (по таблице Питерсона).

4. Выбор неприводимых многочленов в качестве сомножителей образующего полинома т.о., чтобы

набор корней содержал непрерывную цепь корней длиной не менее чем m=d_min-1=2t;

Представление в виде произведения неприводимых сомножителей.

Этап декодирования аналогичен ц.к. При этом l>1.

Построить ц.к. для передачи различных символов, исправляющий одну или две ошибки:

k = [log₂N] = [log₂100] = 7, d_min5.

n = k + r = 7 + 2*h  2 n – 1; h = 4; r = l*h = 2*4 = 8 n = 15.

x 15 +1 = (x+1)(x 2 +x+1)(x 4 +x+1)(x 4 +x 3 +1)(x 4 +x 3 +x 2 +x+1).

4. f_3*f₅ = (x 4 +x+1)(x 4 +x 3 +x 2 +x+1)

В качестве F(x) _, _₄,_, ₇, ₉₁₀,₁₃

f_4*f₅ = (x 4 +x 3 +1)(x 4 +x 3 +x 2 +x+1)

При выборе в качестве порождающего F₁(x) или F₂(x) – корректирующие возможности полученного ц.к. будут равны.

Степень образующего многочлена F(x) = 8;

F(x) = F₁(x) = (x 4 +x+1)(x 4 +x 3 +x 2 +x+1) = x 8 + x 7 + x 6 + x 4 + 1.

C_15,7 = 0000001 11010001 W(E_i)  d_min = 5;

10000,00000,00000 111010001

11101,0001

Необходимо закодировать и передать: Н=1000011

1100001 01001101 Ex) = 1101011|01001101,

2). Циклический сдвиг на 4 позиции

3). Ц.к. влево на 2 позиции

4). Циклический сдвиг вправо на 4 + 2 = 6 позиций.

После этого получаем направленную кодовую комбинацию.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

I. Общие положения

1. Декодирование циклических кодов (бчх-кодов)

1.1. Принцип синдромного декодирования бчх-кодов

В основу рассматриваемой процедуры деко­дирования циклических кодов положен алгоритм синдромного деко­дирования. Это означает, что при приеме кодовой комбинации циклического кода рассчитывается синдром – вектор, который показывает величину (вид) и место ошибки.

Согласно рассматриваемой модели двоичного дискретного канала связи, в котором возможны только ошибки перехода, искажение приводит к инверсии символа кодовой комбинации. Поэтому возникновение ошибок при передаче кодовой комбинации циклического кода можно представить следующей аддитивной моделью:

(1.1)

где e(x) – полином ошибки; V(x) – передаваемый полином; – принятый полином.

Разделим обе части представленного уравнения на порождающий полином g(x):

Из представления полинома V(x) известно, что он делится на порождающий полином g(x) без остатка. Назовем синдромом остаток (вычет), который образуется в результате деления полинома на порождающий полином g(x). Согласно правилам операций над вычетами можно оставить только их в обеих частях уравнения. Поэтому выражение можно представить в следующем виде:

(1.2)

Из приведенного выражения очевидно, что синдром, рассчитываемый по принятому полиному (кодовому векторуV’), однозначно определяет полином ошибки e(x) (вектор ошибки e), который воздействовал на полином V(x) во время передачи по каналу связи. Поэтому, заранее определив возможные значения синдрома для разных вариантов ошибок и сравнив их с рассчитанным по конкретному полиному (кодовому векторуV’) значением синдрома, можно определить полином ошибки e(x) (вектор ошибки e). Зная полином (вектор) ошибки, можно реализовать корректирующие свойства кода, направив их на исправление и/или обнаружение ошибки (стирание сообщения). Очевидно, что при безошибочной передаче (e(x)=0) синдром тоже равен 0.

Определим, какое количество вариантов полинома ошибки необходимо рассчитать для наиболее сложной корректирующей операции – исправления ошибок. Указанное значение N определяется как

(1.3)

где s – кратность исправляемых ошибок; n – общая длина кодовой комбинации циклического кода.

Как известно из верхней границы Хэмминга, количество разных вариантов синдромов (2 k ) достаточно для однозначного соответствия каждому виду s-кратной ошибки,

Оценим сложность устройства, которое реализует сравнение рассчитанного значения синдрома и заранее определенных значений r_i(x). Количество элементов должно быть равно N. Поскольку указанное устройство осуществляет функции сравнения и выбора, оно получило название декомбинатор синдрома (ДКМС). Поэтому число N в ДКМС определяет количество k-входовых конъюнкторов. Таким образом, можно сделать вывод, что декомбинатор синдрома настраивается на полином ошибки.

Принцип синдромного декодирования применим и к обнаружению ошибок. В данном случае необходимо установить только факт возникновения ошибки. Очевидно следующее условие наличия ошибок: . Поэтому ДКМС в данном случае состоит из одного логического дизъюнктора, который проверяет на равенство 0 полиномS(x).

Для синдромного декодирования кода, исправляющего и обнаруживающего ошибки, можно выделить два способа декодирования: общий и частный. Частный способ может быть применен для декодирования кодов Хэмминга с d_min = 4.

В общем случае обнаружение ошибок, приводящее к стиранию кодовой комбинации, должно произойти в случае, когда синдром , и ни один из элементов (конъюнкторов) ДКМС, настроенных для исправления соответствующей ошибки, не сработал.

В рассматриваемом частном случае для построения циклического кода с четным d_min используется переход от ближайшего кода с нечетным d_min. При этом порождающий полином определяется путем домножения полинома g(x) на полином (1x). В данном конкретном случае при декодировании применяется способ раздельного деления. Это означает, что отдельно рассчитывается синдром S(x) от деления полинома на порождающий полином g(x), а отдельно – на полином (1x). Остаток от деления полинома на полином (1x) имеет нулевую степень, то есть он может быть равен либо 0, либо 1. Это означает, что он указывает четность веса полинома . Синдром S(x) рассчитывается для обнаружения места ошибки. Рассмотрим варианты соотношения векторов синдрома на примере БЧХ-кода с d_min = 4 (табл. 1.1).

mod g(x)

mod (1x)

Источник