Что будет если умножить cos на cos

Ещё немного о тригонометрии в вычислениях

На Хабре было уже много статей, посвящённых быстрым вычислениям тригонометрии, когда сильно надо, но я хотел бы дополнить их одной небольшой заметкой с отсылкой к школьной тригонометрии.

Иногда может не быть аппаратной реализации тригонометрии, иногда могут быть иные причины, чтобы изобретать методы ускорения вычисления.

Математика

Давайте вспомним некоторые простые формулы из школьного курса.

Начнём с простых:
(1)

Косинус/синус любого угла может быть приведён к аргументу в диапазоне от 0° до 45°, используя формулы первой группы.

Для малых углов тригонометрические функции могут быть сведены к асимптотическим разложениям, если отбрасываемые члены заведомо выходят за разрядную сетку.

Все промежуточные углы могут быть получены суммированием больших углов с некоторым шагом (а для них тригонометрию можно считать таблично), и остатков, которые рано или поздно дадут линейное разложение.

Применение

Дальше нужно будет выбрать шаг таблиц исходя из того, как мы хотим распределить вычисления, показатель степени 11 мы разделим на несколько частей. Например, можно разбить его на две части: 11=6+5, тогда нам понадобятся две таблицы размером 64 и 32 записи (итого 96), или на три части: 11=4+4+3 (размер таблиц 16+16+8=40 записей), но будет больше операций умножения — конкретный выбор будет зависеть от задачи и располагаемых ресурсов.

Ремарка: запись в таблице — это пара синус и косинус аргумента. Если храним с одинарной точностью, то размер записи 8 байт.

Пример

Давайте для примера возьмём разложение 4+4+3, а потом обобщим.

Шаг 1. Приведём аргумент x к нашей шкале, поделив его на константу pi/4 (назовём его x’ ).

[предположим для примера, что получился синус]

Шаг 3. Воспользуемся таблицами (напомню, что их 3), при этом индексами в таблице будут «битовые поля» в двоичном представлении аргумента x» — первые 4 бита после запятой, потом ещё 4, и ещё 3, а оставшиеся не при делах биты пойдут в остаток.

Табличные синус назовём S1, S2, S3, табличные косинусы — C1, C2, C3.

Шаг 4. Объединяем всё, что получилось:

Шаг 5. Если на шаге 2 мы сочли, что результат должен получиться отрицательным, то этот минус надо ввести в результат.

Заключение

Аналогичный подход может использоваться как для вычисления в вещественных числах любого размера, так и, например, для реализации специализированной арифметики с фиксированной запятой. Собственно, в своё время именно последняя задача меня и сподвигла поковыряться в эту сторону, но это было давно.

Источник

sin(a+b), cos(a+b), sin(a-b), cos(a-b). Формулы сложения в аргументе синуса и косинуса

Эти формулы позволяют:

• Вычислять значения тригонометрических функций нестандартных углов

• Легко и просто получать формулы двойного угла

Пример. Докажите тождество \(\sin⁡2x=2 \sin⁡x \cos⁡x\).
Решение. \(\sin⁡2x=\sin⁡(x+x)=\)\(\sin⁡x \cos⁡x+\cos⁡x \sin⁡x=2 \sin⁡x \cos⁡x\).

Пример. Докажите тождество \(\cos⁡2x=\cos^2⁡x-\sin^2⁡x\).
Решение. \(\cos⁡2x=\cos⁡(x+x)=\)\(\cos⁡x \cos⁡x-\sin⁡x \sin⁡x=\cos^2⁡x-\sin^2⁡x\).

• И даже формулы приведения:

Как запомнить формулы сложения

Как видите, формулы сложения достаточно полезны и их стоило бы хорошенько выучить. Однако с этим часто возникают трудности, т.к. они похожи и сложно запомнить их точно.

Тут мы дадим вам несколько подсказок и придуманное нами мнемоническое правило, благодаря которому вы через пять минут напишите все формулы верно, ничего не заучивая. Не верите? Давайте проверим!

[ исходная функция ]\(=\)[ функция1 ]·[ функция2 ] \(±\) [ функция3 ]·[ функция4 ]

— во-вторых, обратите внимание, что в каждой формуле все функции справа – разные. У нас есть две функции (\(sin\)⁡ и \(cos\)⁡) и два аргумента (\(x\) и \(y\), и из всего этого богатства получается четыре варианта:

Вот их мы и будем расставлять в окошки справа.
Тут же заметим, что у функций, стоящих в паре, всегда разные аргументы: \(x\) и \(y\).

— в-третьих, отметьте, что начало правой части формулы всегда такое же как начало левой части:

То есть, уже на данном этапе вы можете часть формулы сходу написать: нужен вам, например, косинус суммы – вы сразу пишете

\(\cos⁡(x+y)\)\(=\)\(\cos⁡x\)·[ функция2 ] \(±\) [ функция3 ]·[ функция4 ]

И осталось только определить, что будет стоять вместо знака вопроса (плюс или минус) да расставить в окошки оставшиеся три функции: \(\sin⁡x\), \(\sin⁡y\) и \(\cos⁡y\). Вот тут-то нам и приходит на помощь мнемоническое правило.

И осталось только определить, что будет стоять вместо знака вопроса (плюс или минус) да расставить в окошки оставшиеся три функции: \(\sin⁡x\), \(\sin⁡y\) и \(\cos⁡y\). Вот тут-то нам и приходит на помощь мнемоническое правило.

Звучит оно следующим образом: «косинусы закомплексованы и всё у них наперекосяк». Фраза дурацкая, странная и созвучная: «косинус-комплекс-косяк», поэтому сама по себе запоминается легко, а означает она следующее:

— косинусы закомплексованы: поэтому, когда мы пишем формулу для сумму или разности косинусов, справа косинусы «общаются» (в смысле, стоят рядом) только с косинусами. Соответственно, синусам остается «общаться» только с синусам. Таким образом, в получаемой нами формуле имеем:

— всё у них наперекосяк: то есть, у формул косинуса знак слева и справа – разный. В нашем случае слева плюс, значит справа ставим минус:

Давайте для отработки получим формулу разности в синусе (со всеми рассуждениями):

\(\sin⁡(x-y)=\sin x\)·[ функция2 ] \(±\) [ функция3 ]·[ функция4 ]

— закомплексованы у нас косинусы, но мы-то пишем формулу для синуса, а они вполне себе «общительные» – значит рядом с синусом будет стоят косинус, причем с другим аргументом (игреком):

— наперекосяк всё в жизни у косинусов, а у синусов всё стабильно, так что знак сохраняется:

Теперь попробуйте сами – еще раз просмотрите основные моменты статьи, а потом возьмите чистый лист и, никуда не подглядывая, напишите все формулы.
Ну как, получилось?

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение тригонометрических уравнений.

Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Немного теории.

Тригонометрические уравнения

Уравнение cos(х) = а

Уравнение cos x = а, где \( |a| \leqslant 1 \), имеет на отрезке \( 0 \leqslant x \leqslant \pi \) только один корень. Если \( a \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right] \); если a

Уравнение sin(х) = а

Уравнение tg(х) = а

Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.

Решение тригонометрических уравнений

Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.

Уравнения, сводящиеся к квадратным

Уравнение вида a sin(x) + b cos(x) = c

Используя формулы \( \sin(x) = 2\sin\frac <2>\cos\frac<2>, \; \cos(x) = \cos^2 \frac <2>-\sin^2 \frac <2>\) и записывая правую часть уравпения в виде \( 2 = 2 \cdot 1 = 2 \left( \sin^2 \frac <2>+ \cos^2 \frac <2>\right) \) получаем

В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях \( a \neq 0, \; b \neq 0, \; c \neq 0, \; c^2 \leqslant b^2+c^2 \) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на \( \sqrt \):

Решить уравнение 4 sin(x) + 3 cos(x) = 5

Здесь a = 4, b = 3, \( \sqrt = 5 \). Поделим обе части уравнения на 5:

Уравнения, решаемые разложением левой части на множители

Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.

Источник

Коэффициент мощности косинус фи — наглядное объяснение простыми словами.

Многие из вас наверняка видели на электроинструментах, двигателях, а также люминесцентных лампах, лампах ДРЛ, ДНАТ и других, такие надписи как косинус фи — cos ϕ.

Однако люди далекие от электротехники и позабывшие школьные уроки физики, не совсем понимают, что же означает данный параметр и зачем он вообще нужен.

Предположим перед вами есть 2 проводника. Один из этих проводников имеет потенциал. Не суть важно какой именно — отрицательный (минус) или положительный (плюс).

У другого провода вообще нет никакого потенциала. Соответственно между этими двумя проводниками будет разность потенциалов, т.к. у одного он есть, а у другого его нет.

Если вы соедините кончики двух проводов не непосредственно между собой, а через лампочку накаливания, то через ее вольфрамовую нить начнет протекать ток. От одного провода к другому.

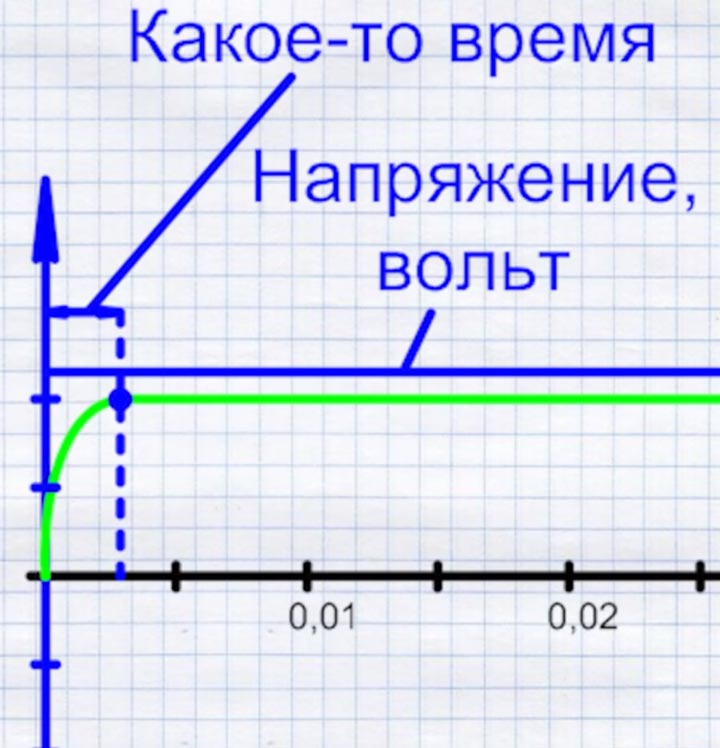
В какой-то момент он его достигает и держится на этом уровне постоянно. То же самое будет, если подключить не одну, а две, три лампочки и т.д.

А что случится, если вместе с лампой последовательно включить катушку, намотанную из множества витков проволоки?

Изменится ли как-то процесс нарастания тока? Конечно, да.

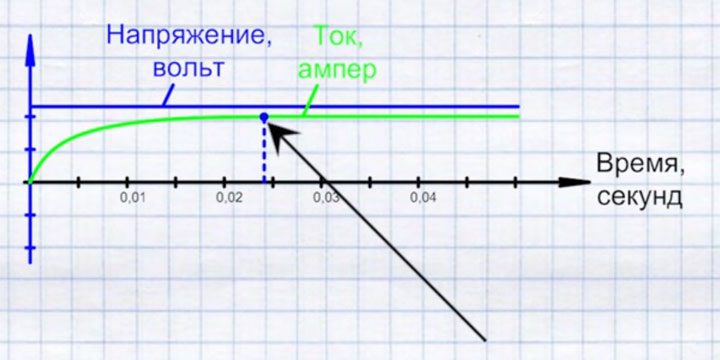
Данная катушка индуктивности, заметно затормозит время увеличения тока от нуля до максимума. Фактически получится, что максимальное напряжение (разность потенциалов) на лампе уже есть, а вот ток поспевать за ним не будет.

Его нарастание слишком медленное. Из-за чего это происходит и кто виноват? Виноваты витки катушки, которые оказывают влияние друг на друга и тормозят ток.

Если у вас напряжение постоянное, например как в аккумуляторах или в батарейках, ток относительно медленно, но все-таки успеет дорасти до своего номинального значения.

А далее, ток будет вместе с напряжением идти, что называется «нога в ногу».

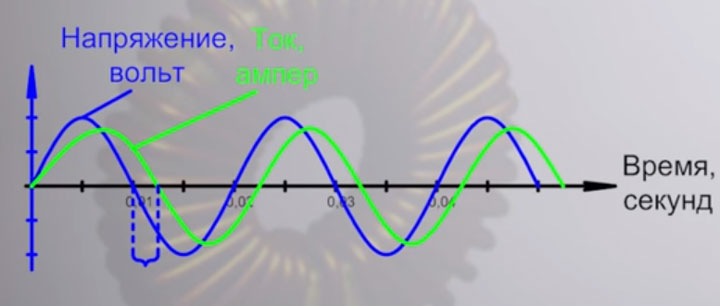
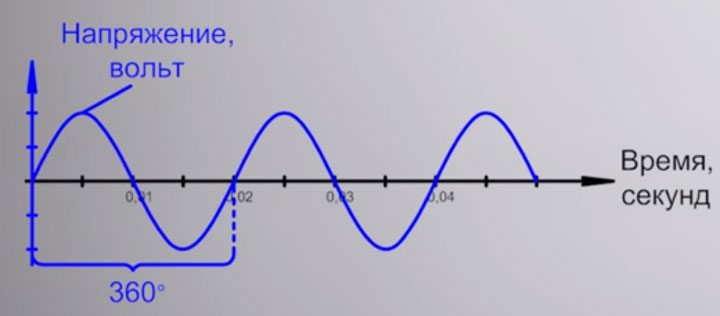
А вот если взять напряжение из розетки, с переменной синусоидой, то здесь оно не постоянно и будет меняться. Сначала U какое-то время положительная величина, а потом — отрицательная, причем одинаковое по амплитуде. На рисунке это изображается в виде волны.

Эти постоянные колебания не дают нашему току, проходящему сквозь катушку, достигнуть своего установившегося значения и догнать таки напряжение. Только он будет подбираться к этой величине, а напряжение уже начинает падать.

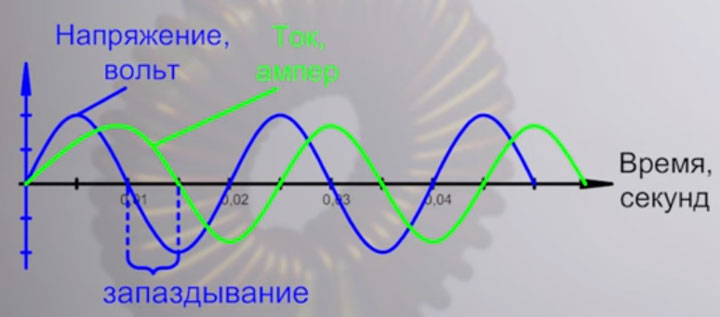
Причем, чем больше в катушке намотано витков, тем большим будет это самое запаздывание.

Как же это все связано с косинусом фи — cos ϕ?

А связано это таким образом, что данное отставание тока измеряется углом поворота. Полный цикл синусоиды или волны, который она проходит от нуля до нуля, вместив в себя максимальное и минимальное значение, измеряется в градусах. И один такой цикл равен 360 градусов.

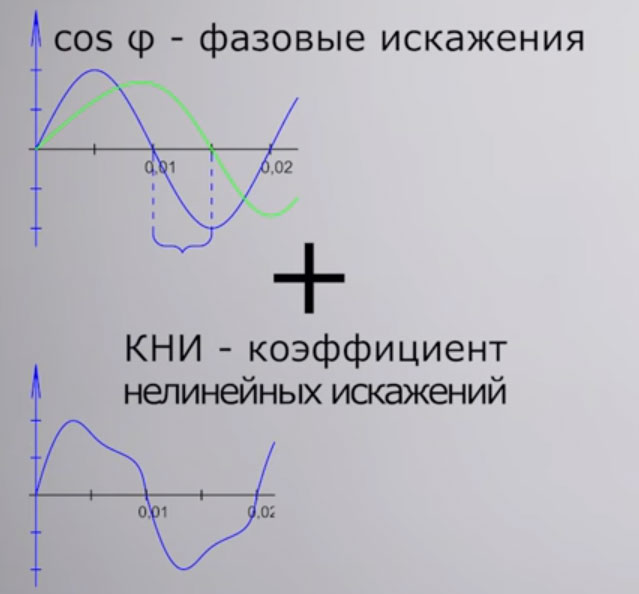
А вот угол отставания тока от напряжения, как раз таки и обозначается греческой буквой фи. Значение косинуса этого угла опаздывания и есть тот самый cos ϕ.

Таким образом, чем больше ток отстает от напряжения, тем большим будет этот угол. Соответственно косинус фи будет уменьшаться.

По научному, ток сдвинутый от напряжения называется фазовым сдвигом. При этом почему-то многие уверены, что синусоида всегда идеальна. Хотя это далеко не так.

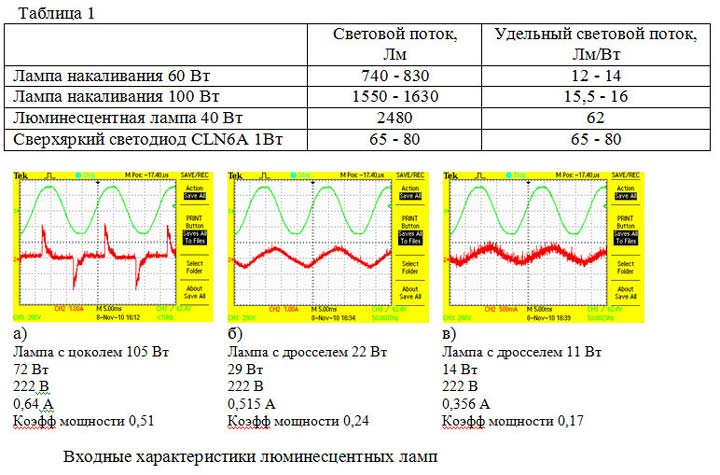
В качестве примера можно взять импульсные блоки питания.

Не идеальность синусоиды выражается коэфф. нелинейных искажений — КНИ. Если сложить две эти величины — cos ϕ и КНИ, то вы получите коэффициент мощности.

Однако, чтобы все не усложнять, чаще всего под понятием коэфф. мощности имеют в виду только лишь один косинус фи.

На практике, данный коэффициент мощности рассчитывают не при помощи угла сдвига фаз, а отношением активной мощности к полной.

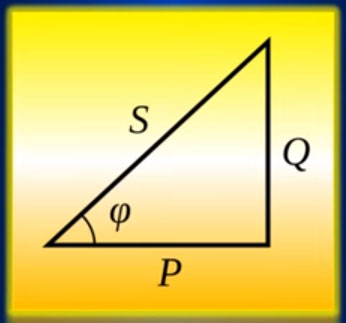
Существует такое понятие как треугольник мощностей. Сам косинус — это тригонометрическая функция, которая и появилась при изучении свойств прямоугольных треугольников.

Она здорово помогает производить определенные вычисления с ними. Например, наглядно показывает отношение длин прилежащего катета (P-активная мощность) к гипотенузе (S-полная мощность).

То есть, зная угол сдвига, можно узнать, сколько активной мощности содержится в полной. Чем меньше этот угол, тем меньше реактивной составляющей находится в сети, и наоборот.

В КПД все более четко — полезная мощность используется на нагрев — охлаждение — механическую работу, остальное уходит безвозвратно. Эта разница и показывается в КПД.

Более подробно, с графиками, рисунками и простыми словами, без особых научных формулировок обо всем этом говорится в ролике ниже.

Рассмотренное запаздывание тока относительно напряжения — это не хорошее явление. Как оно может сказаться на ваших лампочках или проводке?

Часть энергии будет просто «болтаться» в катушке, при этом не принося никакой пользы. Правда не пугайтесь, ваш бытовой счетчик реактивную энергию не считает и платить вы за нее не будете.

Например, если вы включите в розетку инструмент или светильник с полной мощностью 100Ва, на блоке питания которого будет указано cos ϕ=0,5. То прибор учета накрутит вам только на половину от этой величины, то есть 50Вт.

Вот известное наглядное видео, демонстрирующее последствия этого для проводки.

Казалось бы, выбрось катушку и вся проблема исчезнет. Однако делать этого нельзя.

В большинстве светильников, лампы работают не отдельно, а в паре с источниками питания. И в этих самых источниках, как раз таки присутствуют разнообразные катушки.

Катушки просто необходимы как функциональная часть всей схемы и избавиться от них не получится. Например в тех же дроссельных лампах ДРЛ, ДНАТ, люминесцентных и т.п.

Поэтому характеристика коэфф. мощности, здесь больше относится к блоку питания, нежели к самой лампе. Данный cos ϕ может принимать значение от ноля до единицы.

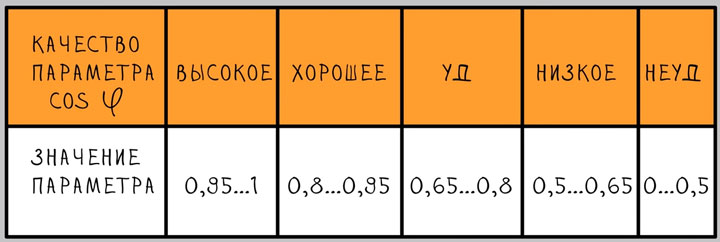
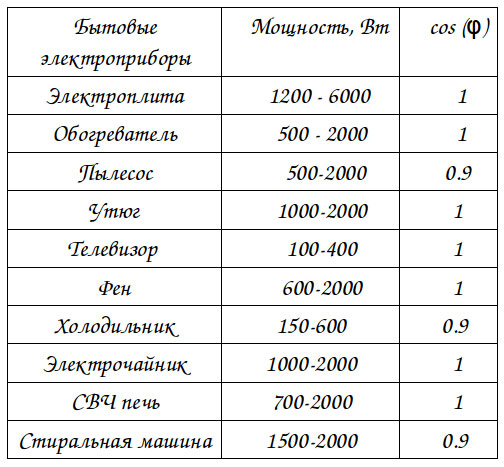
Чем выше коэффициент мощности, тем ниже потери электроэнергии. Вот таблица косинуса фи для различных потребителей:

Если вы не знаете точный коэфф. мощности своего прибора, или его нет на бирке, можно ли измерить косинус фи в домашних условиях, не прибегая к различным формулам и вычислениям? Конечно можно.

Подключая любое оборудование через него, можно легко без замеров и сложных вычислений, узнать фактический cos ϕ.

Зачастую, фактические данные могут быть даже точнее, чем написанные на шильдике, которые рассчитаны для идеальных условий.

Если он слишком низкий, что делать, чтобы привести его значение как можно ближе к единице? Можно это дело определенным образом компенсировать. Например, с помощью конденсаторов.

Источник

Тригонометрические уравнения. Как решать тригонометрические уравнения?

Тригонометрические уравнения – уравнения, содержащие переменную под знаком тригонометрических функций.

Как решать тригонометрические уравнения:

Любое тригонометрическое уравнение нужно стремиться свести к одному из видов:

\(\sin ⁡x=a\) \(⇔\) \( \left[ \beginx=\arcsin a+2πn, n∈Z\\ x=π-\arcsin a+2πl, l∈Z\end\right.\)
если \(a∈[-1;1]\)

Пример. Решите тригонометрическое уравнение \(\sin⁡x=-\)\(\frac<1><2>\).
Решение:

Внимание! Уравнения \(\sin⁡x=a\) и \(\cos⁡x=a\) не имеют решений, если \(a ϵ (-∞;-1)∪(1;∞)\). Потому что синус и косинус при любых икс больше или равны \(-1\) и меньше или равны \(1\):

Ответ: \(x=\) \(\frac<π><4>\) \(+πk\), \(k∈Z\).

Пример. Решите тригонометрическое уравнение \(\cos⁡(3x+\frac<π><4>)=0\).
Решение:

7) Дальше решать в таком виде несколько трудновато, разобьем уравнение на два.

8) Как обычно в уравнениях будем выражать \(x\).
Не забывайте относиться к числам с \(π\), так же к \(1\), \(2\), \(\frac<1><4>\) и т.п. Это такие же числа, как и все остальные. Никакой числовой дискриминации!

Рассмотрим пример решения квадратно-тригонометрического уравнения

Пример. Решите тригонометрическое уравнение \(2\cos^2⁡x-5\cos⁡x+2=0\)
Решение:

Сделаем замену \(t=\cos⁡x\).

\(D=25-4 \cdot 2 \cdot 2=25-16=9\)

Делаем обратную замену.

Первое уравнение решаем с помощью числовой окружности.
Второе уравнение не имеет решений т.к. \(\cos⁡x∈[-1;1]\) и двум быть равен не может ни при каких иксах.

Ответ: \(x=±\) \(\frac<π><3>\) \(+2πk\), \(k∈Z\).

Пример решения тригонометрического уравнения с исследованием ОДЗ:

Пример(ЕГЭ). Решите тригонометрическое уравнение \(\frac<2\cos^2⁡x-\sin<⁡2x>>\) \(=0\)

Потому ОДЗ для ctg\(x\): \(\sin⁡x≠0\).

Отметим «нерешения» на числовой окружности.

Источник

• ← Что будет если уменьшить человека
• Что будет если умножить бесконечность на бесконечность →