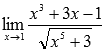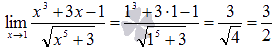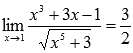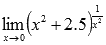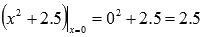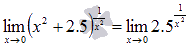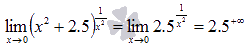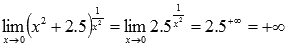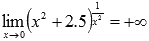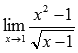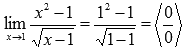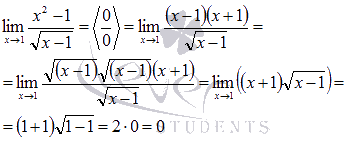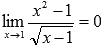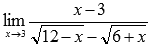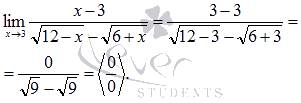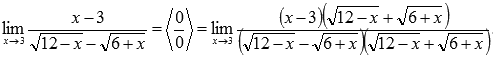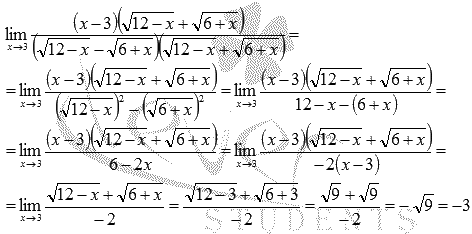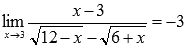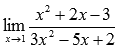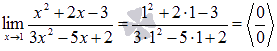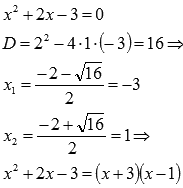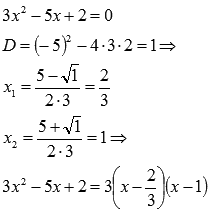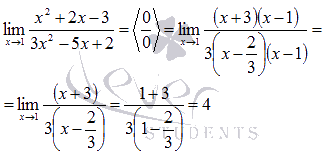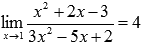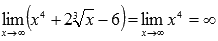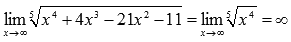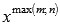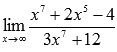Что будет если умножить бесконечность на бесконечность

Что будет если умножить бесконечность на бесконечность

многое можно, изучите для начала математическикий анализ, а потом

уже сюда со своими измышлениями.

Почитайте про мощность множеств

и на тыщу можно умножить. и на мульён.

Ибо и там, и там количество отрезков будет бесконечное количество.
Ты хочешь переплюнуть Чака Норриса, который сосчитал до бесконечности, притом дважды?
Эх, и где ты учился? Явно не в лицее.

Высшую математику не изучали? Хотя сейчас и программе среднего образования есть.

Почитайте раздел ряды, пределы.

дайте мне точку опоры и т.д.

Салют! Конечно все можно, но что сними будешь делать когда разделишь?

но у этого кабеля должны быть концы. Потомучто концы идут бесконечно дальнему жителю вселенной. Правильно? конечно верно.

Какой же бред ты несешь!

У бесконечного кабеля будет бесконечный вес, больше, чем масса Вселенной, потому что даже масса Вселенной конечна, и главное, у бесконечного кабеля будет бесконечная стоимость,!

а с чего ты взял что масса вселенной конечна?

В каждый момент времени конечна, на сколько я помню. Просто ростёт постоянно.

ммм во сне приснилось :)?

масса не может расти. Масса вселенной либо бесконечна, если вселенная бесконечна, либо конечна если вселенная конечна. а конечна вселенная или бесконечна это пока не известно.
ну и понятным образом нельзя запихать бесконечный кабель в конечную вселенную 🙂

На сколько известно всё имеет массу в космосе если не ошибась 4% кислорода, он так же имеет массу, ну а что вселенная ростёт еже секундно.. даже спорить не собераюсь.

ну и не спорь 🙂 ты ведь даже элементарных понятий не знаеш, куда уж в споры лезть 🙂

в видимой вселенной 99.99% вещества это водород. кислорода там кот наплакал.

«ты ведь даже элементарных понятий не знаеш, куда уж в споры лезть»

http://novolitika.ru/news/59874
По чаще сам себя перед зеркалом цитируй.

если ты походу даже не знаеш чем отличаются объём и масса, а ещё тут чето выпендриваешся 🙂

Уахаха))) это называется бред пытающегося заснуть)))

А вы тут сразу с оскорблениями.
Конечно все в свое время «изучали» высшую математику. Но честно признаюсь, от тех лекций у мну в голове мало что осталось.
Всем отличного дня, с пятницей 🙂

Изучите высшую математику, там всё есть.

А зачем вообще умножать бесконечность, если она и так бесконечность.

Ну про то я и говорю.

Умножать бесконечность такая же бессмыслица, как и умножать ноль. Бесконечность это всегда бесконечность, хоть дели ее на триллион, хоть умножай на триллион. А ноль всегда останется нолем, это ничто, пустота, тоже хоть дели ее, хоть умножай на бесконечность. Допустим у вас нуль золота, хоть на тысячу умножай, нуль золота у вас нулем и останется.

кстати распределение один день на свободе один в тюрме

ничуть не лучше и не хуже любого другого способа разбиения бесконечности на две бесконечности. можно например 1000 лет на свободе 1 день в тюрме. точно так же это приведёт к тому что он проведёт и в тюрме и на свободе бесконечное количество дней. а можно и 1 год в тюрме 1 час на свободе. тоже самое.
и эти бесконечности ничуть не хуже бесконечностей которые получились при деление на дни один к одному

Он просто разрешил зеку половину жизни прожить

на свободе, а половину в тюрьме.

Но для отдельно взятого человека срок «пожизненный» эквивалентен «бесконечному»

Сразу видно что не математик.

Практически все изучали высшую математику в ВУЗе, так что, не надо.

По мне анекдот на 100% соответствует и поддерживает тему топа

Это вы куда то не туда свернули

Не я рассказал этот анекдот.

Но не надо же переходить на тему кого и как наказывать.

Ладно, всё пучком 🙂 Улыбнись и пой 🙂 На vesmir.ya1.ru увидел смешной пост (не совсем политкорректный, но всё же), посмеялся :)))

Дайте прямую ссылку на пост

Тоже охота посмеяться )

http://vesmir.ya1.ru/6946-trolling-na-vysshem-urovne-ne-vosprinimaem-slishkom-serezno.html
Наверное, с газом переборщили :)))

Когда математику ставят задачу: вычислить устойчивость стула, то он сразу выдает ответы на стул с бесконечным числом ножек и с нулевым кол-вом ножек.
А остальную часть своей жизни тратит на определение устойчивости с n-м количеством..

Тем и плохи математики, что им ставят задачу другие спецы, они не способны сами поставить задачу и решить ее. Тогда как последние сами себе ставят задачу и сами же её решают :DDD

квадратный стул с 4 ножками по углам не менее устойчив чем квадратный стул с любым другим количеством ножек. при 4 ножках по углам достигается максимальная устойчивость и больше она уже не станет.
странно не зная математики лезть и говорить что будут делать математики в данном случае.
З.Ы. кстати я математик

вселенная не ростет, а расширяется с возрастающей скоростью

чак норрис досчитал до бесконечности. два раза=)))

Конечно можно.
одну бесконечность умножить на два бесконечности получится два бесконечности.
К одной бесконечности прибавить еще два бесконечности получится три бесконечности.

для человека всегда будет равное количество в той и другой линии, поскольку одна и вторая линия бесконечны, что говорит о том, что они всегда в образе или представление человека будут одинаковы не достижимы, следовательно каждая точка из линий соответствует количеству осизаемого представления о линиях, но парадокс заключается в том, что человек зная что в одной линии больше точек будет считать что именно в этой линии их больше, но если представить бесконечность, то всегда ответ будет один, каждая линия будет стримится к уравниванию точек, поскольку бесконечность линий соразмерна количеству точек в каждой из них, что в итоге подведет движение этих точек к общему знаминателю или проще говоря ни одна точку ни окажится меньшей по отношению к другой точки находящейся в другой линии, поскольку обе они бесконечны, а раз так то бесмысленно проводить такой эксперемент, а следовательно количество точек также бесконечно как и длина обоих линий))), глупо сказать, что в одной бесконечной линии точек больше чем в другой бесконечной линии, если точек также бесконечно))) вы не находите?

А что получится если от бесконечности отнять бесконечность? Ноль?

В данном случае если со второй линии убавим первую, то получится не ноль, а бесконечность (через каждые 2 метра) 🙂

Получится Неопределенность вида бесконечность минус бесконечность

1.В математике не существует одного понятия бесконечности, она наделяется особыми свойствами в каждом разделе. Более того, эти различные «бесконечности» не взаимозаменяемы. К примеру, теория множеств подразумевает разные бесконечности, причём одна может быть больше другой. Скажем, количество целых чисел бесконечно большое (оно называется счётным). Чтобы обобщить понятие количества элементов для бесконечных множеств, в математике вводится понятие мощности множества. При этом не существует одной «бесконечной» мощности. Например, мощность множества действительных чисел больше мощности целых чисел, потому что между этими множествами нельзя построить взаимно-однозначное соответствие (биекцию), а целые числа включены в действительные. Таким образом, в этом случае «число элементов» (мощность) одного множества «бесконечней» «числа элементов» (мощности) другого. Основоположником этих понятий был немецкий математик Георг Кантор.

Эти бесконечные точки.

Бесконечны только в таком виде.
Конечны в отрезке. И там точно будет в два раза больше.
Думаю умножить бесконечность допустимо, в этом случае бесконечная либо раздваиваться, превращаясь к примеру в две линии. Или два ряда цифр.
Если бесконечно абстрактная, то увеличивается её плотность. Может быть для бесконечности есть понятие плотности. Ведь воображаемый цифровой бесконечный раз разряден единице.
В данном случае бедет множиться плотность бесконечных точек. Но количество всё равно будет бесконечным. Так что это думаю не важно.

отрезок не может быть

бесконечным, это можно вырозить следующим образом.
линия равна 100 что к примеру в нашем случае будет равнятся условно бесконечности, отрезок к примеру в 1 не может быть частью бесконечности. поскольку он то есть 1 соответствует размеру 1, что ни может быть бесконечностью, следовательно «отризать» у бесконечности что-то не представляется возможным, поскольку данная часть всегда будет даже не частью бесконечности, а нечто другим несовместимым с бесконечностью, поскольку последняя стремится 100 условной бесконечности, в таком случае малая часть то есть 1 конечно будет иметь энное количество точек и что конечно покажит наличия в одной линии больше точек, но отрезак 1 ни когда не будет частью бесконечности, поскольку бесконечность в моем представление усечь нельзя, тогда это уже не бесконечность. в данном случае отрезок равный 1 есть данность, что не совместимо с бесконечностью вы согласны?

Источник

Уроки математики: почему нельзя делить на ноль

Очень часто многие задаются вопросом, почему же нельзя использовать деление на ноль? В этой статье мы очень подробно расскажем о том, откуда появилось это правило, а также о том, какие действия можно выполнять с нолем….

Ноль можно назвать одной из самых интересных цифр. У этой цифры нет значения, она означает пустоту в прямом смысле слова. Однако, если ноль поставить рядом с какой-либо цифрой, то значение этой цифры станет больше в несколько раз.

Число очень загадочно само по себе. Его использовал еще древний народ майя. У майя ноль означал «начало», а отсчет календарных дней также начинался с нуля.

Очень интересным фактом является то, что знак ноля и знак неопределенности у них были похожи. Этим майя хотели показать, что ноль является таким же тождественным знаком, как и неопределенность. В Европе же обозначение нуля появилось сравнительно недавно.

Также многим известен запрет, связанный с нолем. Любой человек скажет, что на ноль нельзя делить. Это говорят учителя в школе, а дети обычно верят им на слово. Обычно детям либо просто не интересно это знать, либо они знают, что будет, если, услышав важный запрет, сразу же спросить «А почему нельзя делить на ноль?». Но когда становишься старше, то просыпается интерес, и хочется побольше узнать о причинах такого запрета. Однако существует разумное доказательство.

Действия с нулем

Для начала необходимо определить, какие действия с нулем можно выполнять. Существует несколько видов действий:

Важно! Если при сложении к любому числу прибавить ноль, то это число останется прежним и не поменяет своего числового значения. То же произойдет, если от любого числа отнять ноль.

При умножении и делении все обстоит немного иначе. Если умножить любое число на ноль, то и произведение тоже станет нулевым.

Запишем это как сложение:

Всего складываемых нолей пять, вот и получается, что

Попробуем один умножить на ноль. Результат также будет нулевым.

Ноль также можно разделить на любое другое число, не равное ему. В этом случае получится дробь, значение которой также будет нулевым. Это же правило действует и для отрицательных чисел. Если ноль делить на отрицательное число, то получится ноль.

Также можно возвести любое число в нулевую степень. В таком случае получится 1. При этом важно помнить, что выражение «ноль в нулевой степени» абсолютно бессмысленно. Если попытаться возвести ноль в любую степень, то получится ноль. Пример:

Пользуемся правилом умножения, получаем 0.

Это интересно! Свойства натуральных логарифмов: график, основание, функции, предел, формулы и область определения

Так можно ли делить на ноль

Итак, вот мы и подошли к главному вопросу. Можно ли делить на ноль вообще? И почему же нельзя разделить число на ноль при том, что все остальные действия с нулем вполне существуют и применяются? Для ответа на этот вопрос необходимо обратиться к высшей математике.

Начнем вообще с определения понятия, что же такое ноль? Школьные учителя утверждают, что ноль-это ничто. Пустота. То есть когда ты говоришь, что у тебя 0 ручек, это значит, что у тебя совсем нет ручек.

В высшей математике понятие «ноль» более широкое. Оно вовсе не означает пустоту. Здесь ноль называют неопределенностью, так как если провести небольшое исследование, то получается, что при делении ноля на ноль мы можем в результате получить любое другое число, которое не обязательно может быть нолем.

Знаете ли вы, что те простые арифметические действия, которые вы изучали в школе не так равноправны между собой? Самыми базовыми действиями являются сложение и умножение.

Для математиков не существует понятий «деление» и «вычитание». Допустим: если от пяти отнять три, то останется два. Так выглядит вычитание. Однако, математики запишут это таким образом:

Таким образом, получается, что неизвестной разностью является некое число, которое нужно прибавить к 3, чтобы получить 5. То есть, не нужно ничего вычитать, нужно просто найти подходящее число. Это правило действует для сложения.

Немного иначе дела обстоят с правилами умножения и деления. Известно, что умножение на ноль приводит к нулевому результату. Например, если 3:0=х, тогда, если перевернуть запись, получится 3*х=0. А число, которое умножалось на 0 даст ноль и в произведении. Получается, что числа, которое бы давало в произведении с нолем какую-либо величину, отличную от ноля, не существует. А значит, деление на ноль бессмысленно, то есть оно подходит к нашему правилу.

Но что будет, если попытаться разделить сам ноль на себя же? Возьмем как х некое неопределенное число. Получается уравнение 0*х=0. Его можно решить.

Если мы попробуем взять вместо х ноль, то мы получим 0:0=0. Казалось бы, логично? Но если мы попробуем вместо х взять любое другое число, например, 1, то в конечном итоге получится 0:0=1. Та же ситуация будет, если взять любое другое число и подставить его в уравнение.

В этом случае получится, что мы можем как множитель взять любое другое число. Итогом будет бесконечное множество разных чисел. Порой все же деление на 0 в высшей математике имеет смысл, но тогда обычно появляется некое условие, благодаря которому мы сможем все-таки выбрать одно подходящее число. Это действие называется «раскрытием неопределенности». В обычной же арифметике деление на ноль снова потеряет свой смысл, так как мы не сможем выбрать из множества какое-то одно число.

Важно! На ноль нельзя разделить ноль.

Ноль и бесконечность

Бесконечность очень часто можно встретить в высшей математике. Так как школьникам просто не важно знать о том, что существуют еще математические действия с бесконечностью, то и объяснить детям, почему делить на ноль нельзя, учителя как следует не могут.

Основные математические секреты ученики начинают узнавать лишь на первом курсе института. Высшая математика предоставляет большой комплекс задач, которые не имеют решения. Самыми известными задачами являются задачи с бесконечностью. Их можно решить при помощи математического анализа.

К бесконечности также можно применить элементарные математические действия: сложение, умножение на число. Обычно еще применяют вычитание и деление, но в конечном итоге они все равно сводятся к двум простейшим операциям.

Но что будет, если попытаться:

Важно! Бесконечность немного отличается от неопределенности! Бесконечность является одним из видов неопределенности.

Теперь попробуем бесконечность делить на нуль. Казалось бы, должна получиться неопределенность. Но если мы попробуем заменить деление умножением, то получится вполне определенный ответ.

Источник

Сколько будет 1000 умножить на бесконечность

Что будет если 0 умножить на бесконечность?

Что будет если 0 умножить на бесконечность? Каждый человек еще со школьных уроков помнит, что делить на ноль нельзя. В школе это заучивается как прописная истина.

Такое правило существует по той причине, что любое деление на ноль в рамках математической науки будет подразумевать результат, равный бесконечности. И если вопрос о делении рождает заученный ответ, то с умножением все не так просто. Но ответ на вопрос о том, что будет, если 0 умножить на бесконечность, найти не столь трудно. Так каким же будет результат подобного умножения?

И в рамках школьного курса, и знакомясь с основами высшей математики в университете, существуют операции, проводимые с нулем. Его умножают, вычитают, прибавляют. Однако 0 подразумевает под собой пустоту, полное отсутствие чего-либо. Если к 3 прибавить 0, то результат останется равный тройке. Операция умножение же будет предполагать результат, равный нулю. Эта информация известна со школьной скамьи. Потому в рамках простых чисел не возникает вопросов. А что же с умножением нуля на бесконечность? Подобная операция – прием не запрещенный. Однако конечный результат может удивить, в рамках него легко проводится параллель с делением на 0. Если провести операцию умножения нуля на бесконечность, то в результате получится все та же бесконечность, но состоящая из нулей. Таким образом, с помощью подобного действия невозможно получить какое-либо числовое значение, даже приближенное к сверхбольшим числам.

Делить на 0 запрещено. Так учили в школе. Но если поразмышлять, то деление на ноль даст ответ бесконечность. Под бесконечностью здесь понимается не все числа вместе взятые, а какое-то абстрактное число, которое больше любого другого. То есть, число без границ. Так, например деление 3 на 0.1 даст 30; 3 на 0.01 – 300; 3 на 0.0000001 даст 30000000. Как видно, чем ближе число к нулю, тем больше нулей будет после числа в ответе. Тем большим будет число. В итоге, если поделить на сам 0, будет число с бесконечным числом нулей после него. Поскольку нулей бесконечно, то это число равно бесконечности.

2. Умножение 0 на бесконечность.

3. Возведение 0 в степень 0.

Пока что напишу об этих трех вещах, которые заметил. Может быть позже напишу еще о некоторых.

С непосредственным вычислением пределов основных элементарных функций разобрались.

При переходе к функциям более сложного вида мы обязательно столкнемся с появлением выражений, значение которых не определено. Такие выражения называют неопределенностями.

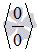
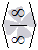
Перечислим все основные виды неопределенностей: ноль делить на ноль ( 0 на 0 ), бесконечность делить на бесконечность , ноль умножить на бесконечность , бесконечность минус бесконечность , единица в степени бесконечность , ноль в степени ноль , бесконечность в степени ноль .

ВСЕ ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.

Раскрывать неопределенности позволяет:

Сгруппируем неопределенности в таблицу неопределенностей. Каждому виду неопределенности поставим в соответствие метод ее раскрытия (метод нахождения предела).

Эта таблица вместе с таблицей пределов основных элементарных функций будут Вашими главными инструментами при нахождении любых пределов.

Приведем парочку примеров, когда все сразу получается после подстановки значения и неопределенности не возникают.

Вычислить предел

Подставляем значение:

И сразу получили ответ.

Вычислить предел

Подставляем значение х=0 в основание нашей показательно степенной функции:

То есть, предел можно переписать в виде

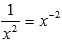
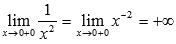
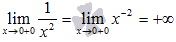
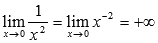
Теперь займемся показателем. Это есть степенная функция . Обратимся к таблице пределов для степенных функций с отрицательным показателем. Оттуда имеем и , следовательно, можно записать .

Исходя из этого, наш предел запишется в виде:

Вновь обращаемся к таблице пределов, но уже для показательных функций с основанием большим единицы, откуда имеем:

Разберем на примерах с подробными решениями раскрытие неопределенностей преобразованием выражений.

Очень часто выражение под знаком предела нужно немного преобразовать, чтобы избавиться от неопределенностей.

Вычислить предел

Подставляем значение:

Пришли к неопределенности. Смотрим в таблицу неопределенностей для выбора метода решения. Пробуем упростить выражение.

После преобразования неопределенность раскрылась.

Вычислить предел

Подставляем значение:

Пришли к неопределенности ( 0 на 0 ). Смотрим в таблицу неопределенностей для выбора метода решения и пробуем упростить выражение. Домножим и числитель и знаменатель на выражение, сопряженное знаменателю.

Для знаменателя сопряженным выражением будет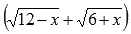

Знаменатель мы домножали для того, чтобы можно было применить формулу сокращенного умножения – разность квадратов и затем сократить полученное выражение.

После ряда преобразований неопределенность исчезла.

ЗАМЕЧАНИЕ: для пределов подобного вида способ домножения на сопряженные выражения является типичным, так что смело пользуйтесь.

Вычислить предел

Подставляем значение:

Разложим числитель на множители:

Разложим знаменатель на множители:

Наш предел примет вид:

После преобразования неопределенность раскрылась.

Рассмотрим пределы на бесконечности от степенных выражений. Если показатели степенного выражения положительны, то предел на бесконечности бесконечен. Причем основное значение имеет наибольшая степень, остальные можно отбрасывать.

Пример.

Пример.

Если выражение под знаком предела представляет собой дробь, причем и числитель и знаменатель есть степенные выражения ( m – степень числителя, а n – степень знаменателя), то при 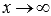возникает неопределенность вида бесконечность на бесконечность , в этом случае неопределенность раскрывается делением и числитель и знаменатель на

Вычислить предел

Источник