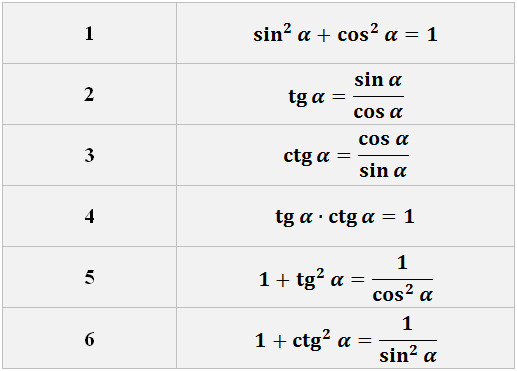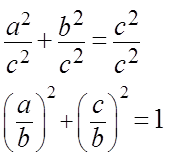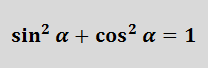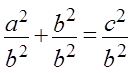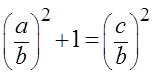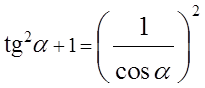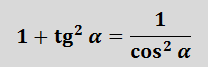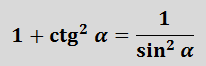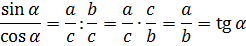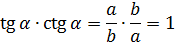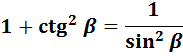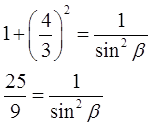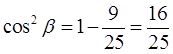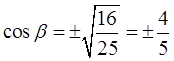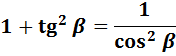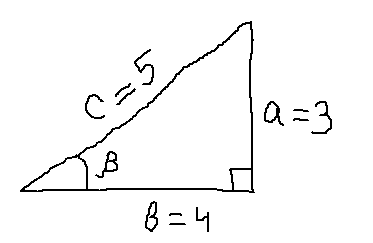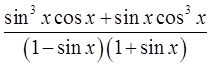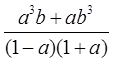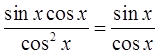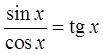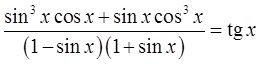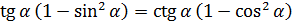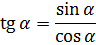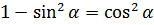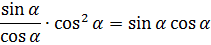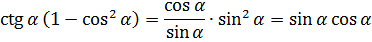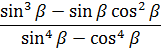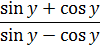Что будет если умножить косинус на косинус одного угла

Произведение синусов и косинусов: формулы, примеры

Приведем формулы произведения синуса на синус, косинуса на косинус и синуса на косинус.

Формулы произведения. Список

Приведем формулировки, а затем и сами формулы.

Для любых α и β справедливы формулы

Вывод формул

Вывод описанных выше формул проводится с помощью формул сложения и на основе свойства равенства. Согласно этому свойству, если левую и правую части верного равенства сложить соответственно с левой и правой частями другого верного равенста, то в результате получится еще одно верное равенство. Покажем вывод формул произведения.

Сначала запишем формулы косинуса суммы и косинуса разности:

Сложим эти равенства и получим:

Формула произведения косинусов доказана.

Перепишем формулу косинуса суммы следующим образом:

Таким образом, выведена формула произведения синусов.

Теперь возьмем формулу синуса суммы, формулу синуса разности, и сложим их левые и правые части

Формула произведения синуса на косинус выведена.

Примеры использования

Приведем примеры использования формул произведения синусов, косинусов и синусов на косинус при решении задач.

Теперь вычислим значение выражения, обратившись к таблице основных значений тригонометрических функций.

Таким образом, мы проверили формулу на практике и убедились, что формула справедлива.

Пример. Формулы произведения

Нужно sin 75 ° умножить на cos 15 ° и вычислить точное значение произведения.

Мы не располагаем точными значениями синуса и косинуса данных углов, однако можем вычислить точное значение произведения sin 75 ° · cos 15 ° c помощью формулы произведения синуса на косинус.

Также формулы произведения используются преобразования тригонометрических выражений.

Источник

Произведение синусов и косинусов, вывод формул, примеры.

Изучение основных формул тригонометрии продолжаем формулами произведения синусов, косинусов и синуса на косинус. Эти формулы являются в определенном смысле обратными формулам суммы синусов и косинусов, то есть, позволяют от произведения синусов и косинусов углов и перейти к сумме или разности синусов и косинусов углов и .

В этой статье мы рассмотрим следующие формулы: произведение синусов, произведение косинусов и произведение синуса на косинус, покажем их вывод, а также приведем примеры их использования.

Навигация по странице.

Список формул

Запишем по порядку формулы произведения синусов, косинусов и синуса на косинус.

Эти формулы справедливы для любых углов и .

Озвучим формулировки данных формул произведения:

Вывод формул

Формулы произведения синусов, косинусов и синуса на косинус можно вывести, основываясь на формулах сложения, а также на следующем свойстве равенств: если к левой и правой части верного равенства прибавить соответственно левую и правую части другого верного равенства, то получится верное равенство.

Для вывода формул произведения синусов и косинусов нам потребуются формулы косинуса суммы и косинуса разности вида и .

Сложив эти равенства, получаем , откуда следует, что и . Так доказана формула произведения косинусов.

Если же формулу косинуса суммы переписать как , после чего к этому равенству прибавить равенство , то легко получается формула произведения синусов вида .

Для вывода формулы произведения синуса на косинус достаточно сложить левые и правые части формул синуса суммы и синуса разности . Имеем , откуда следует, что .

Так мы вывели формулы произведения синусов, косинусов и синуса на косинус.

Примеры использования

Разберем несколько примеров использования формул произведения синусов, косинусов и синуса на косинус. Это сделаем для того, чтобы было понятно, как применяются рассматриваемые формулы для конкретных углов.

Начнем с того, что проверим справедливость, например, формул произведения синусов. Для этого возьмем , и убедимся, что для этих углов совпадают значения правой и левой частей равенства . Имеем (при необходимости обращайтесь к разделу таблица значений синуса, косинуса, тангенса и котангенса), и

Так как мы получили одинаковые значения, то формула произведения синусов справедлива для данных углов.

В некоторых случаях формулы произведения позволяют вычислять значения тригонометрических выражений. Рассмотрим пример, подтверждающий наши слова.

Вычислите точное значение произведения синуса 75 градусов и косинуса 15 градусов.

Точные значения и нам неизвестны, поэтому мы не можем непосредственно вычислить требуемое значение. Однако ответить на вопрос задачи нам позволяет формула произведения синуса и косинуса. Действительно, сумма углов 75 и 15 градусов равна 90 градусов, а их разность равна 60 градусов, для данных углов мы знаем точные значения всех тригонометрических функций.

Итак,

.

Формулы произведения синусов, косинусов, синуса и косинуса используются для преобразования тригонометрических выражений, но эта тема требует более детального обсуждения.

Источник

Произведение косинусов, синусов и синуса на косинус

Формулы произведений косинусов cos(α)×cos(β), синусов sin(α)×sin(β) и синуса на косинус sin(α)×cos(β) можно выразить из четырех базовых формул — косинуса разности cos(α−β), косинуса суммы cos(α+β), синуса разности sin(α−β) и синуса суммы sin(α+β):

cos(α−β) = cos(α)×cos(β) + sin(α)×sin(β) (I) cos(α+β) = cos(α)×cos(β) − sin(α)×sin(β) (II) sin(α−β) = sin(α)×cos(β) − cos(α)×sin(β) (III) sin(α+β) = sin(α)×cos(β) + cos(α)×sin(β) (IV)

Эти четыре формулы вывести трудно, поэтому их проще запомнить. Но с их помощью можно вывести искомые тригонометрические тождества.

Произведение косинусов

Сложим базовые равенства I и II — косинус разности и косинус суммы:

cos(α−β) + cos(α+β) = = cos(α)×cos(β) + sin(α)×sin(β) + cos(α)×cos(β) − sin(α)×sin(β) = <одинаковые произведения синусов сокращаются>= cos(α)×cos(β) + cos(α)×cos(β) = 2×cos(α)×cos(β)

cos(α−β) + cos(α+β) = 2×cos(α)×cos(β)

В этом равенстве можно и левую и правую части поделить на 2 и поменять местами и получится искомое выражение для произведения косинусов:

cos(α)×cos(β) = [cos(α−β) + cos(α+β)] / 2,

т.е. произведение косинусов равно полусумме косинуса разности и косинуса суммы.

Произведение синусов

Воспользуемся базовыми формулами I и II — косинус разности и косинус суммы. Из равенства I вычтем равенство II:

cos(α−β) — cos(α+β) = = cos(α)×cos(β) + sin(α)×sin(β) — cos(α)×cos(β) + sin(α)×sin(β) = <одинаковые произведения косинусов сокращаются>= sin(α)×sin(β) + sin(α)×sin(β) = 2×sin(α)×sin(β)

cos(α−β) — cos(α+β) = 2×sin(α)×sin(β)

В этом равенстве можно левую и правую части поделить на 2 и поменять местами и получится искомое выражение для произведения синусов:

sin(α)×sin(β) = [cos(α−β) — cos(α+β)] / 2,

т.е. произведение синусов равно полуразности косинуса разности и косинуса суммы.

Произведение синуса на косинус

Сложим базовые равенства III и IV — синус суммы и синус разности:

sin(α−β) + sin(α+β) = = sin(α)×cos(β) − cos(α)×sin(β) + sin(α)×cos(β) + cos(α)×sin(β) = <одинаковые cos(α)×sin(β) сокращаются>= sin(α)×cos(β) + sin(α)×cos(β) = = 2×sin(α)×cos(β)

sin(α−β) + sin(α+β) = 2×sin(α)×cos(β)

В этом равенстве можно левую и правую части поделить на 2 и поменять местами и получится искомое выражение для произведения синуса на косинус:

sin(α)×cos(β) = [sin(α−β) + sin(α+β)] / 2,

т.е. произведение синуса на косинус равно полусумме синуса разности и синуса суммы.

Итоговые формулы произведения косинусов, синусов и синуса на косинус

cos(α)×cos(β) = [cos(α−β) + cos(α+β)] / 2 sin(α)×sin(β) = [cos(α−β) — cos(α+β)] / 2 sin(α)×cos(β) = [sin(α−β) + sin(α+β)] / 2

Эти формулы мы получили из четырех базовых формул: косинуса разности cos(α−β), косинуса суммы cos(α+β), синуса суммы sin(α−β) и синуса разности sin(α+β). И эти четыре равенства мы между собой складывали и вычитали.

Источник

Сумма и разность синусов и косинусов: вывод формул, примеры

Формулы суммы и разности синусов и косинусов

Запишем, как выглядят формулы суммы и разности для синусов и для косинусов

Формулы суммы и разности для синусов

Определения формул сумм и разности синусов и косинусов

Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.

Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.

Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.

Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.

Вывод формул суммы и разности синусов и косинусов

Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже

Также представим сами углы в виде суммы полусумм и полуразностей.

Переходим непосредственно к выводу формул суммы и разности для sin и cos.

Вывод формулы суммы синусов

В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим

Действия по выводу остальных формул аналогичны.

Вывод формулы разности синусов

Вывод формулы суммы косинусов

Вывод формулы разности косинусов

Примеры решения практических задач

Пример 1. Проверка формулы суммы синусов двух углов

Пример 2. Применение формулы разности синусов

С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.

Источник

Связь между тригонометрическими функциями одного угла. Основные тригонометрические формулы.

Итак, в прошлый раз мы с вами успешно познакомились с тригонометрическими функциями — синусом, косинусом, тангенсом и котангенсом. И чётко уяснили себе следующее:

1. Синус, косинус, тангенс и котангенс — это просто какие-то безразмерные числа. Отношения сторон в прямоугольном треугольнике. Для каждого конкретного угла — свои.

2. Тригонометрические функции крепко-накрепко связаны с углом. Знаем угол — знаем и все его тригонометрические функции. И наоборот.

Если не уяснили эти простые вещи, то добро пожаловать по ссылочке, пока не поздно. А мы продолжаем.

То, что между этой великолепной четвёркой существует тесная связь, не вызывает никаких сомнений. Всякая связь в математике задаётся, чаще всего, формулами. В тригонометрии формул — огромное количество. Это и формулы приведения, и формулы сложения, двойного угла, понижения степени и многие-многие другие.

Здесь «альфа» — какой-то угол.

Эти шесть формул — краеугольный камень всей тригонометрии. То, чего не знать нельзя. Если вы не знаете, чему равен, скажем, косинус тройного угла — не проблема. Никто вас не осудит. Но если вы не знаете, что sin 2 x+cos 2 x = 1, то будьте готовы получить заслуженную двойку. Вот так вот.

Из этих формул сразу видно, что они неразрывно связывают между собой синус, косинус, тангенс и котангенс одного и того же угла. Именно эти формулы нам позволяют находить все тригонометрические функции одного и того же угла, если известна хотя бы одна из них. Причём (важно!) не находя сам угол! Такие задания очень популярны как сами по себе, так и могут быть промежуточным этапом в более серьёзных заданиях. В тригонометрических уравнениях, к примеру. И особенно в высшей математике, в тех же пределах, интегралах, дифференциальных уравнениях и прочих крутых темах.

Кстати говоря, хочу обратить ваше внимание на один частый ляп в неправильном написании тригонометрических функций в степенях — в квадрате, в кубе и так далее.

Например, выражение квадрат синуса (или синус в квадрате) в тригонометрии пишется вот так:

Двойка (т.е. степень) в этом случае пишется между углом и названием функции. Эта запись как раз и говорит нам о том, что в квадрат возводится именно сама функция (т.е. в нашем случае — синус).

будет говорить уже о том, что в квадрат возводится, не синус угла, а только сам угол! Почувствуйте разницу, что называется.)

Во избежание путаницы, ещё раз (и навсегда!) всё то же самое, но со скобочками:

sin 2 x = (sin x) 2

sin x 2 = sin(x 2 )

Конечно, заниматься возведением углов в квадрат мы в школьной тригонометрии вряд ли будем. За ненадобностью.) Зато возведением функций в квадрат — постоянно. Так что привыкаем, не путаемся и пишем правильно.

Ну что, посмотрим на вывод основных формул? Чтобы всё встало на свои места. Зачем и почему? Да потому, что любая формула запоминается гораздо проще, если есть возможность её «пощупать» в реале, а не механически зазубривать и бездумно принимать на веру, как само собой разумеющееся.) Тем более что это не просто, а очень просто!

Вывод и смысл основных тригонометрических формул.

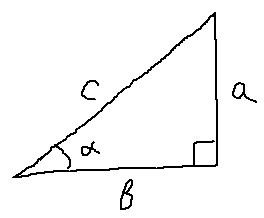
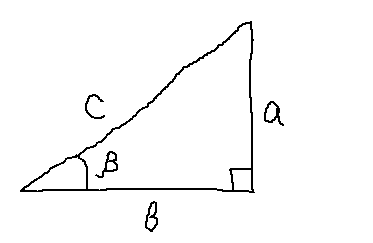
Первым делом, я снова нарисую наш старый добрый прямоугольный треугольник. Не обязательно по линеечке, по клеточкам, а просто схематично. От руки.

Что нам понадобится ещё для дальнейшей работы?

1. Теорема Пифагора:

a 2 + b 2 = c 2

sin α = a/c

cos α = b/c

tg α = a/b

ctg α = b/a

Всё. Вот и все инструменты.

А вот теперь начинается самое весёлое. Сейчас я беру нашу горячо любимую теорему Пифагора a 2 + b 2 = c 2 и… начинаю всячески над ней издеваться, подвергая её всевозможным пыткам.) Результатами пыток станут целых три формулы из нашего списка!

Так у нас с вами рождается на свет формула №1:

Эта формула — самая популярная во всей тригонометрии! По-другому её ещё называют основным тригонометрическим тождеством.

Она же, но записанная слегка по-другому (в зависимости от того, что именно надо выразить):

Эти две модификации формулы №1 весьма и весьма часто применяются в примерах по тригонометрии! Именно они позволяют легко перевращать синусы в косинусы (и наоборот). Имеет смысл запомнить.

Давайте поделим и посмотрим:

И снова соображаем из тригонометрии (и нашего рисунка), что же такое a/b. Верно, тангенс альфа! А c/b? Так сразу и не скажешь… Стоп! Но ведь что такое b/c — это же нам ясно! Это косинус альфа! У нас же в формуле стоит тот же косинус, только перевёрнутый вверх ногами — c/b. Значит, справа в скобках у нас стоит величина, обратная косинусу: 1/cos α.

Итого имеем следующее:

Переписываем в привычном виде и рождаем формулу №5:

Попробуйте получить самостоятельно, очень полезно.)

Вторая, третья и четвёртая формулы выводятся совсем элементарно, исходя только из определения тригонометрических функций и элементарных действий с дробями. Теорема Пифагора здесь не нужна.

Что, например, у нас получится, если мы просто поделим синус на косинус?

И все дела.) С котангенсом — аналогично.

А если перемножить тангенс и котангенс? Ну-ка, ну-ка…

Вот и вся премудрость. Убедились, насколько всё просто?)

Решение простейших заданий по тригонометрии.

Теория теорией, но нам ведь опыт наращивать надо, верно? Так что пора приступать к задачкам. Всё как всегда — от совсем простых и безобидных до вполне себе серьёзных.

Здесь, ясное дело, надо искать формулу, связывающую тангенс и котангенс. Это четвёртая формула. Самое главное — сообразить, что вместо «альфа» можно писать любую другую букву. Лишь бы везде одна и та же была. Для нашего задания будет:

Можно прямо в эту формулу подставить значение ctg x = 1,25:

Осталось лишь решить это простенькое уравнение. Да-да. Ещё раз подчёркиваю, что любая формула, любое соотношение, соединённое знаком равенства («=»), — это всегда уравнение! А там, где уравнение, там автоматически и тождественные преобразования уравнений, да…

Наше соотношение — это тоже уравнение. Где роль неизвестного играет tg x. Прошу заметить, не икс, а именно весь тангенс целиком! Вас же не смущает уравнение, скажем, y·1,25 = 1? Что вы обычно делаете в таких случаях? Правильно, делите обе части на 1,25, чтобы слева остался чистый игрек. Вот и здесь тоже делим обе части на 1,25, добиваясь слева чистого тангенса.

И все дела. Это и есть верный ответ.

Можно поступить иначе. Сначала выразить из общей формулы тангенс:

А уже теперь подставить вместо ctg x его значение 1,25. Получим то же самое. И так и эдак можно. Разницы — никакой. Но… если осознать смысл этой формулы поглубже, то можно получить очень простой и очень полезный практический приём.

Запоминаем:

Если единицу разделить на котангенс, то получим тангенс. И наоборот, единица, делённая на тангенс, даёт котангенс. Эти две функции взаимно обратны!

Что? Не знаете, как разделить единичку на число? Ну, это вопрос не к тригонометрии. Вопрос к шестому классу, к дробям… Как разделить? Да просто перевернуть это самое число и все дела!

И так далее и тому подобное. В общем, вы поняли…)

Например, классика жанра:

2. Известно, что β — острый угол в прямоугольном треугольнике.

Ищем формулу, связывающую синус и косинус. Это самая первая формула:

Подставляем в неё известную нам величину 0,6 вместо косинуса:

И считаем, как обычно:

Вот, практически, и всё. У нас есть квадрат синуса. А нужен сам синус. Для этого осталось всего лишь извлечь корень и — ответ готов! Корень из 0,64 будет 0,8.

Два разных ответа получается. А нужен один. Второй — неправильный. Что делать? Да всё как обычно! Внимательно прочитать задание! Там зачем-то сказано: «… если β — острый угол…» А лишних слов в заданиях, как правило, не бывает, да… Именно эти слова — и есть дополнительная информация к решению.

Что такое острый угол? Это угол меньше 90 градусов. А у таких углов все тригонометрические функции (в том числе и синус, да…) всегда положительные. То есть, отрицательный ответ мы здесь просто отбрасываем. Имеем полное право.

Собственно, на данном этапе нам такие тонкости особо не нужны. Пока… Ибо сейчас мы работаем только с прямоугольными треугольниками, где углы могут быть только острые. И не знаем, счастливые, что бывают и отрицательные углы, и углы в 1000 градусов… И у всех этих жутких углов тоже есть свои тригонометрические функции! С плюсом и с минусом. Всё от конкретного угла зависит.

А вот старшеклассникам без учёта знака — никак. К сожалению… Но не будем бежать впереди паровоза. Всему своё время.)

Решаем следующую задачку. Покруче.

Определить косинус острого угла β в прямоугольном треугольнике, если ctgβ = 4/3.

На первый взгляд, всё просто. Но попробуем найти в нашем списке формулу, связывающую котангенс и косинус. Ищем и… Вы правы! Такой формулы нету.) Надо как-то выкручиваться…

Можно работать с шестой формулой:

Подставим в эту формулу значение котангенса и преобразуем:

Выразим из этой пропорции (т.е. тоже уравнения!) квадрат синуса:

Итак, квадрат синуса у нас есть. Теперь его легко можно превратить в квадрат косинуса по первой формуле:

cos 2 β = 1 — sin 2 β

Извлекаем корень и определяем сам косинус:

Читаем ещё раз задание и вспоминаем, что у острого угла все тригонометрические функции всегда положительны. Отбрасываем отрицательное значение и получаем окончательный ответ:

Это был один способ. Можно решать и по-другому, через пятую формулу:

Для этого нам надо:

1) Превратить котангенс в тангенс по формуле №4;

2) Подставить значение тангенса в формулу;

3) Преобразовать выражение и выразить из него квадрат косинуса;

4) Извлечь корень и получить два значения косинуса;

5) Сообразить (из условия задания), что в прямоугольном треугольнике все тригонометрические функции всегда положительны. Отбросить отрицательный ответ и получить косинус.

Как видим, хрен редьки не слаще, да.) Но это ещё не всё. Для такого решения надо ещё вспомнить эти формулы! А если забыли? Собственно, в этом-то и кроется главная проблема в их применении. Да ещё и куча вычислений… В общем, не подарок…

Без паники! Для таких задачек есть очень простой и, главное, наглядный способ решения! Геометрический.) Читаем, вникаем и запоминаем.

Нарисуем этот котангенс!

Да-да! Схематично. Как? Очень просто! Берём черновик и рисуем любой прямоугольный треугольник. Кривовато, от руки, даже не соблюдая пропорций. У нас не ИЗО и не черчение с вами.) Выбираем любой острый угол и обозначаем его «бета».

Вспоминаем теперь, что котангенс — это отношение прилежащего катета к противолежащему. И ставим на соответствующих катетах их длины. Какие? А какие в нашем котангенсе записаны! 4 и 3. Противолежащий катет a = 3, а прилежащий b = 4.

Чего ещё нам не хватает для полного счастья? Гипотенузы нам не хватает! Не беда: Пифагор ещё никого не подводил.)

Итак, гипотенуза равна пяти. Подписываем на картинке.)

А теперь считаем косинус прямо по заклинанию: отношение прилежащего катета к гипотенузе.

Всё! Быстро, правда?) Вот такой красивый графический способ-лайт. Безо всяких формул.) Ну… почти. Ведь теорему Пифагора всяко надо знать, да.)

Что, внушает? В таких замороченных примерах необходимо понимать, что синусы и косинусы никоим образом не отменяют всей остальной математики. И подчиняются тем же самым общим правилам, что и обычные числа и буквы в алгебре! А именно — разложение на множители, формулы сокращённого умножения, раскрытие скобок, приведение подобных, сокращение дробей и т.п.

Вас же никак не смущает дробь

правда ведь? Хотя кого-то она, возможно, тоже смущает, да…

Естественно, к основным правилам алгебры добавляется ещё и специфика самой тригонометрии, от этого никуда не денешься. Собственно, с этой целью и разбираем соответствующий пример, да.)

Начнём с числителя нашей здоровенной дроби. Забудем на минутку про тригонометрию и прикинем, что там можно сделать, основываясь на обычных правилах алгебры. Да хотя бы вынести один синус за скобки! Верно, давайте вынесем:

sin 3 x·cos x + sin x·cos 3 x = sin x (sin 2 x·cos x+cos 3 x)

Ой, ещё и косинус вынести можно!

sin x (sin 2 x·cos x+cos 3 x) = sin x·cos x (sin 2 x+cos 2 x)

Вот так. Самые грамотные вообще сразу целиком вынесут произведение sin x·cos x за скобку. Знания и наблюдательность иногда очень помогают. Если они есть.)

А вот теперь и тригонометрия в дело вступает! Что у нас в скобочках? Да! В скобочках у нас — чистая формула №1. Или основное тригонометрическое тождество:

От умножения на единичку выражение не меняется. Значит, числитель нашей дроби будет не что иное, как просто sin x·cos x.

Всё. Числитель упростили до упора. Работаем со знаменателем:

А здесь что? Разность ква… Точно! Разность квадратов! Такая родная и знакомая формула:

Под буквой «a» здесь скрывается единичка, а под буквой «b» — выражение sin x. Ну и что? Важно понимать, что под буквами в алгебраических выражениях может скрываться всё что угодно! И числа, и синусы, и логарифмы, и степени — любые сложные выражения! Алгебре все выражения по плечу. Иначе она не была бы алгеброй, да…)

Вот и срабатываем прямо по формуле разности квадратов:

(1–sin x)(1+sin x) = 1 2 — (sin x) 2 = 1 — sin 2 x

А вот теперь соображаем, уже из тригонометрии, что

Вставляем упрощённые числитель и знаменатель в нашу дробь, сокращаем что сокращается и получаем:

Казалось бы, всё. В рамках алгебры 7-го класса такая дробь дальнейшему упрощению уже не поддаётся, но алгебра в этом примере и так постаралась на славу. Зато в рамках тригонометрии эта дробь вполне себе упрощается! Что же такое синус поделить на косинус? Тангенс, конечно же! Чистая формула №2.

Вот теперь всё. Значит, окончательный результат упрощения вот такой:

Эффект потрясающий, правда?

Запоминаем:

В тригонометрии очень популярны задания, где надо использовать алгебру 7-го класса. А именно — разложение на множители, формулы сокращённого умножения, раскрытие скобок, приведение подобных, сокращение дробей и т.п. Проверяем замороченные примеры на алгебру 7-го класса!

Ещё из той же оперы:

Напоминаю, что страшная фраза «доказать тождество» всего лишь означает, что надо упростить обе части предлагаемого равенства (или какую-то одну, более сложную) и убедиться, что слева и справа стоит одно и то же выражение.

Вот и пробуем добраться до одинакового выражения! Начинаем с левой части. Превращаем тангенс в отношение синуса к косинусу по второй формуле:

Выражение в скобках превращаем в квадрат косинуса по первой формуле:

Подставляем, сокращаем косинусы и получаем:

Ну вот. Левая часть упрощена по максимуму. С правой частью аналогично — формулы №1 и №3 нам в помощь:

Вот и всё! Слева и справа мы получили совершенно одинаковые выражения! А именно — sinα·cosα. Что и требовалось доказать.)

Итак, самое главное.

Чётко уясняем: тригонометрические функции (синус, косинус, тангенс и котангенс) одного угла неразрывно связаны между собой основными тригонометрическими формулами. Если нам известна хотя бы одна из функций — значит, можно (при наличии необходимой дополнительной информации) вычислить и все остальные!

А теперь порешаем, как обычно.

1. Косинус острого угла равен 7/25. Найдите синус этого угла.

2. Известно, что β — угол в прямоугольном треугольнике. Найти tgβ, если sinβ = 15/17.

3. Найдите косинус острого угла A, если известно, что ctg A = 2,4.

5. Упростите выражение и найдите его значение, если sinβ = 1:

6. Известно, что tg y = 3. Найдите значение выражения:

Что, страшно? Мы такого не решали? Да, не решали. Но и самим поразмышлять тоже иногда полезно, да.) Подсказка: основное свойство дроби вам в помощь! Ну и формула №2 для тангенса, само собой.)

Источник