Что будет если умножить корень на корень с одинаковым показателем

Действия с корнями.

Умножение корней с одинаковыми показателями

Чтобы перемножить корни с одинаковыми показателями, нужно оставить тот же показатель корня, а подкоренные выражения перемножить.

√(81) × √(25) =
= √(81 × 25) =
= 9 × 5 =
= 45

Умножение корней с разными показателями

Чтобы перемножить корни с разными показателями, нужно сначала привести корни к общему показателю, а потом перемножить полученные корни с одинаковым показателем. Чтобы умножить корень на число, надо занести под знак корня это число, возведённое в степень с показателем, как у корня.

∛‎(729) × √(25) =
= √(81) × √(25) =
= √(81 × 25) =
= 9 × 5 =
= 45

Деление корней с одинаковыми и разными показателями

Чтобы разделить корни с одинаковыми показателями, нужно разделить подкоренные выражения, а показатель корня оставить прежний.

Если показатели корней разные, то сначала нужно привести корни к общему показателю, а потом — поделить получившиеся корни с одинаковыми показателями.Можно делить (число на корень или корень на число) — для этого нужно занести под знак корня (в числитель или в знаменатель) это число, возведённое в степень с показателем, как у корня.

Возведение корней в степень

Чтобы возвести корень в степень, нужно возвести в эту степень подкоренное выражение, а показатель корня оставить тем же.
(∛‎(125)) 2 = (∛‎(125 2 ))

Извлечение корня из корня

Чтобы извлечь корень из корня, нужно перемножить показатели корней, а подкоренное выражение оставить прежним.

Уничтожение иррациональности в знаменателе

Чтобы избавиться от иррациональности в знаменателе, нужно домножить на одно и то же выражение числитель и знаменатель дроби, пользуясь по мере надобности формулами сокращённого умножения. Если в знаменатетеле дроби корень числа — домножаем на такой же корень, и в знаменателе оказывается само число.

Если в знаменателе дроби сумма/разность корней двух чисел — домножаем на разность/сумму этих корней, и в знаменателе оказывается разность самих чисел.

Если в знаменателе сумма/разность кубических корней двух чисел — домножаем на неполный квадрат разности/суммы этих кубических корней. В знаменателе получается сумма/разность самих чисел.Если в знаменателе неполный квадрат суммы/разности кубических корней двух чисел — домножаем на разность/сумму этих кубических корней. В знаменателе получается разность/сумма самих чисел.

Источник

Корень и его свойства

Тема в математике «Корень и его свойства» нередко вызывает затруднения у школьников, особенно при решении примеров. В данной статье описаны основные свойства корней, а также правила сложения, вычитания, умножения и деления. Наглядные примеры помогаю понять, как решать задания с корнями.

Определение «Корень»

Корень второй степени (квадратный корень) из числа a — это число, которое становится равным a, если число a возвести во вторую степень (в квадрат).
Например, √ 64 = 8 (√ 64 равно числу 8).

Формула: √ a 2 = a

Число, стоящее под знаком корня, называется подкоренным числом. Если под знаком корня стоит целое выражение, то его называют подкоренным выражением.
Свойство квадратного корня: для действительных чисел не существует квадратный корень из отрицательного числа, так как возведение числа в квадрат будет всегда неотрицательным числом.

Извлечение корней: примеры

Найти корень из числа можно одним из следующих способов:

Приведение корней с разными показателями

Для того, чтобы упростить выражение с корнями, которое содержит корни разных степеней, необходимо привести все корни к одной степени.

Например, есть квадратный корень (второй степени √ 2 ) и кубический корень (третьей степени 3 √ 3 ).
Во-первых, необходимо найти наименьшее общее кратное (НОК) для степеней. В нашем примере НОК=6 (2х3).
Во-вторых, применим свойство a = n √ a n : √ 2 = 2 √ 2 = 6 √ 2 3 = 6 √ 8 ; 3 √ 3 = 6 √ 3 2 = 6 √ 9
Получилось два корня одинаковой степени, с которыми можно совершать различные математические действия.

Корень: сложение и вычитание корней

Основное правила сложения и вычитания квадратных корней: сложение и вычитание квадратного корня возможны только при условии одинакового подкоренного выражения.

Примеры:
2√ 3 + 3√ 3 = 5√ 3
2√ 3 + 2√ 4 – не выполняется.

Алгоритм действия:
1. Упростить подкоренное выражение путем разложения на простые множители.
2. Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня.
3. После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
4. У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!

Корень: умножение

Умножение корней без множителей

Произведение корней из чисел равно корню из произведения этих чисел.
√ a*b =√ a *√ b
Важно: между собой можно умножать только одинаковые степени корней, то есть можно умножить один квадратный корень на другой, но нельзя умножить квадратный корень на корень кубической степени.
Примеры:
√ 2 х √ 3 = √ 6
√ 6 х √ 3 = √ 18 = √ 3х3х2 = 3√ 2

Умножение корней с множителями

При умножении корней с множителями нужно отдельно перемножить множители и подкорневые выражения (числа). Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Примеры:
3√ 2 х √ 5 = (3х1) √ (2*5) = 3√ 10
4√ 2 х 3√ 3 = (3х4) √ (2х3) = 12√ 6

Корень: деление

Основной правило деления — подкоренные выражения делятся на подкоренные выражения, а множители на множители.
√ a:b =√ a :√ b
В процессе деления квадратных корней дроби упрощаются.

Деление корней без множителей

Частное корней из чисел равно корню из частного этих чисел.
Важно: между собой можно делить только одинаковые степени корней, то есть можно делить один квадратный корень на другой, но нельзя делить квадратный корень на корень кубической степени.
Пример. √ 21 :√ 3 =√ 21:3 =√ 7

Деление квадратных корней с множителями

Примеры для практики

Чтобы попрактиковаться решать примеры на вычисление квадратный корней, можно скачать программу «Корни квадратные«

Источник

Умножение корней: методы и применение

Известно, что знак корня является квадратным корнем из некоторого числа. Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.

Если вы хотите узнать, как умножить корни «с» или «без» множителей, то эта статья для вас. В ней мы рассмотрим методы умножения корней:

Метод умножения корней без множителей

Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.

Далее необходимо перемножить числа под корнем.

Пример 1: 18 × 2 = 36

Пример 2: 10 × 5 = 50

Пример 3: 3 3 × 9 3 = 27 3

Упростить подкоренные выражения. Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:

Метод умножения показателей с множителями

Умножить множители. Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:

Умножить числа под знаком корня. Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:

Пример 1: 3 2 × 10 = 3 ( 2 × 10 ) = 3 20

Пример 2: 4 3 × 3 6 = 12 ( 3 × 6 ) = 12 18

Упростить подкоренное выражение. Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня. После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:

Пример 1: 3 20 = 3 ( 4 × 5 ) = 3 ( 2 × 2 ) × 5 = ( 3 × 2 ) 5 = 6 5

Пример 2: 12 18 = 12 ( 9 × 2 ) = 12 ( 3 × 3 ) × 2 = ( 12 × 3 ) 2 = 36 2

Метод умножения корней с разными показателями

Найти наименьшее общее кратное (НОК) показателей. Наименьшее общее кратное — наименьшее число, делящееся на оба показателя.

Необходимо найти НОК показателей для следующего выражения:

Записать каждое выражение с новым показателем:

Найти числа, на которые нужно умножить показатели, чтобы получить НОК.

2 → 5 6 = 5 2 6 3 → 2 6 = 2 3 6

Возвести в степень выражения и записать результат под знаком корня:

5 2 6 = ( 5 × 5 ) 6 = 25 6 2 3 6 = ( 2 × 2 × 2 ) 6 = 8 6

Перемножить числа под корнем:

( 8 × 25 ) 6

Записать результат:

( 8 × 25 ) 6 = 200 6

По возможности необходимо упростить выражение, но в данном случае оно не упрощается.

Источник

Перемножение корней с одинаковыми основаниями

Как происходит перемножение корней с одинаковыми основаниями

Теорема умножения корней с одинаковыми основаниями: корень из произведения пары неотрицательных чисел определяется, как произведение квадратных чисел.

Правило применимо в том случае, когда требуется объединить различные числа под одним знаком корня, либо при необходимости представить запись выражения в виде произведения:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Области применения теоремы:

В последнем случае число возводят в степень, соответствующую показателю корня, и записывают под знаком корня, таким образом:

Существует ограничение в данной теореме. Недопустимо умножать корни, которые имеют разные показатели.

Примеры решения задач

\(\sqrt<36 \cdot 64 9>=\sqrt <36>\cdot \sqrt <64>\cdot \sqrt<9>=6 \cdot 8 \cdot 3 = 144\)

\(\sqrt<7056>=\sqrt<2^4+3^3+7^2>=\sqrt <2^4>\cdot \sqrt <3^2>\cdot \sqrt <7^2>= 2^2 \cdot 3 cdot 7 =84\)

Решение примеров с помощью обобщения теоремы

Решение типичных задач на применение теоремы умножения корней основано на упрощении иррациональных выражений. При извлечении корней из 32 и 2 было получено произведение, которое являлось точным квадратом, корень из которого определяется рациональным числом. Отдельно вычислить \(\sqrt<32>\) и \(\sqrt<2>\) не представляется возможным. В последнем примере в обоих подкоренных выражениях находятся дробные числа. С помощью произведения удалось сократить многие из множителей, что позволило оптимально преобразовать все выражение.

Умножать можно не только пары, но и несколько корней. Правило справедливо и в этом случае. Целесообразно рассмотреть применение теоремы на примерах:

Во втором выражении третий множитель имеет под корнем десятичную дробь. В процессе преобразований она была заменена обычной дробью, что позволило выполнить сокращение. Благодаря исключению из иррациональных выражений десятичных дробей, существенно упрощается их решение.

В задачах нередко встречаются корни с произвольной степенью n. При этом можно воспользоваться правилом умножения корней. Таким образом, чтобы перемножить два корня степени n, требуется перемножить их подкоренные выражения, после чего результат записать под одним радикалом.

В качестве примеров можно вычислить следующие выражения:

Во втором случае в процессе умножения кубических корней была исключена десятичная дробь. В результате знаменатель принял вид произведения чисел 625 и 25. Так как данное число большое, целесообразно выделить точный куб в числителе и знаменателе, чтобы применить одно из ключевых свойств корня n-й степени:

Умножение корней с разными показателями

Равенство справедливо лишь в том случае, когда подкоренные выражения обладают неотрицательными значениями. Примеры решения задач:

Требования к неотрицательным значениям подкоренных выражений связано с разными определениями корней четной и нечетной степени. Они обладают разными областями определения.

Перед умножением корней следует преобразовать подкоренные выражения, чтобы они приняли неотрицательные значения. Например, число \(\sqrt[3]<-5>\) можно избавить от знака минус из-под корня. Дальнейшие действия:

Наиболее правильным и надежным методом умножения корней является следующий алгоритм:

Необходимо упростить выражение:

При одинаковых и нечетных показателях корней сложность в решении задачи заключается в наличии минуса у второго множителя. После вынесения знака минус выражение достаточно легко преобразовать:

Требуется упростить выражение:

В данном случае не получится избавиться от корня полностью, но с помощью стандартного алгоритма действий выражение приобретает упрощенный вид:

Источник

Умножение корней: основные правила

Приветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать). Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.

Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)

Вы ведь тоже ещё не вкурили?

Урок получился довольно большим, поэтому я разделил его на две части:

Тем, кому не терпится сразу перейти ко второй части — милости прошу. С остальными начнём по порядку.

Основное правило умножения

. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:

Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.

Примеры. Рассмотрим сразу четыре примера с числами:

Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.

Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.

Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:

И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.

Случай произвольного показателя

В общем, ничего сложного. Разве что объём вычислений может оказаться больше. Разберём парочку примеров:

И вновь внимание второе выражение. Мы перемножаем кубические корни, избавляемся от десятичной дроби и в итоге получаем в знаменателе произведение чисел 625 и 25. Это довольно большое число — лично я с ходу не посчитаю, чему оно равно.

Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:

Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?

При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)

Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.

Умножение корней с разными показателями

Да конечно можно. Всё делается вот по этой формуле:

Однако эта формула работает только при условии, что подкоренные выражения неотрицательны. Это очень важное замечание, к которому мы вернёмся чуть позже.

А пока рассмотрим парочку примеров:

Как видите, ничего сложного. Теперь давайте разберёмся, откуда взялось требование неотрицательности, и что будет, если мы его нарушим.:)

Умножать корни несложно

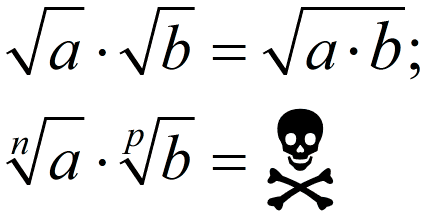
Почему подкоренные выражения должны быть неотрицательными?

Конечно, можно уподобиться школьным учителям и с умным видом процитировать учебник:

Требование неотрицательности связано с разными определениями корней чётной и нечётной степени (соответственно, области определения у них тоже разные).

Ну что, стало понятнее? Лично я, когда читал этот бред в 8-м классе, понял для себя примерно следующее: «Требование неотрицательности связано с *#&^@(*#@^#)

%» — короче, я нихрена в тот раз не понял.:)

Поэтому сейчас объясню всё по-нормальному.

Сначала выясним, откуда вообще берётся формула умножения, приведённая выше. Для этого напомню одно важное свойство корня:

Но есть одна проблема, которая резко ограничивает применение всех этих формул. Рассмотрим вот такое число:

Минус мы убрали как раз потому, что квадрат сжигает минус (как и любая другая чётная степень). А теперь выполним обратное преобразование: «сократим» двойку в показателе и степени. Ведь любое равенство можно читать как слева-направо, так и справа-налево:

Но тогда получается какая-то хрень:

В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)

Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.

Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:

Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.

Чувствуете разницу? Если оставить минус под корнем, то при возведении подкоренного выражения в квадрат он исчезнет, и начнётся хрень. А если сначала вынести минус, то можно хоть до посинения возводить/убирать квадрат — число останется отрицательным.:)

Таким образом, самый правильный и самый надёжный способ умножения корней следующий:

Ну что? Потренируемся?

Это самое простой вариант: показатели корней одинаковы и нечётны, проблема лишь в минусе у второго множителя. Выносим этот минус нафиг, после чего всё легко считается.

Пример 2. Упростите выражение:

Здесь многих смутило бы то, что на выходе получилось иррациональное число. Да, так бывает: мы не смогли полностью избавиться от корня, но по крайней мере существенно упростили выражение.

Вот на это задание хотел бы обратить ваше внимание. Тут сразу два момента:

Например, можно было поступить так:

По сути, все преобразования выполнялись лишь со вторым радикалом. И если не расписывать детально все промежуточные шаги, то в итоге объём вычислений существенно снизится.

Ну что ж, с умножением корней разобрались. Теперь рассмотрим обратную операцию: что делать, когда под корнем стоит произведение?

Источник