Что будет нарисовано после выполнения чертежником алгоритма 207

12.07.202212.07.2022 admin 0 Comments

Что будет нарисовано после выполнения чертежником алгоритма 207

ГДЗ по Информатике. 6 класс. Босова. Рабочая тетрадь

Ursun

Дата: Понедельник, 12.10.2015, 17:58 | Сообщение # 46

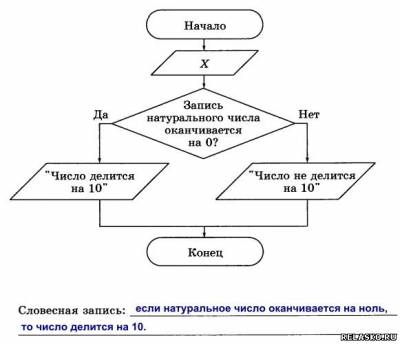
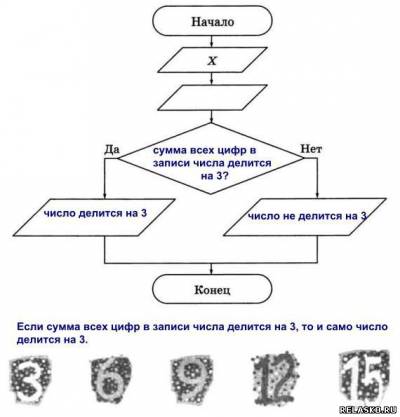
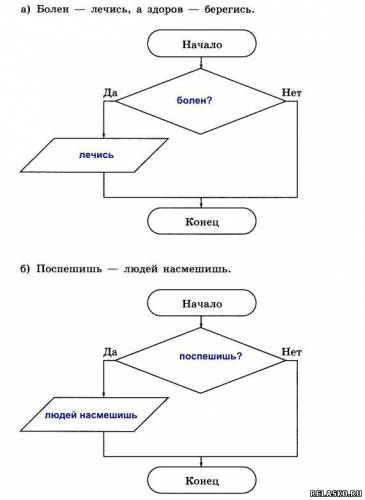
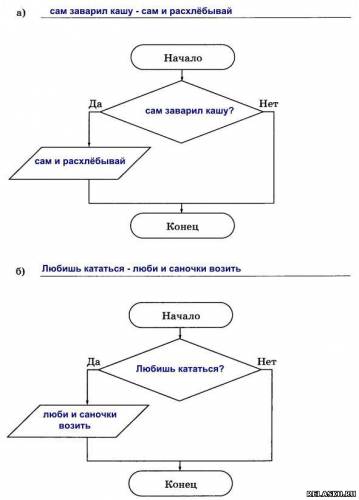
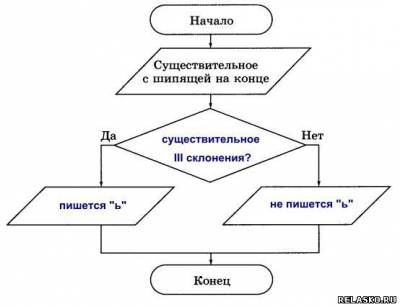
Что бы посмотреть решение и правильный ответ на задачки из рабочей тетради по Информатике Босова нажмите на картинку

191. Внимательно рассмотрите блок-схему. Сформулируйте в словесной форме признак, о котором в ней идёт речь.

192. Оформите в виде блок-схемы признак делимости натурального числа на 3.

193. Запишите с помощью блок-схем следующие пословицы
194. Вспомните пословицы, которые можно записать в виде следующих блок-схем.
195. В конце существительных III склонения после шипящих в формах именительного и винительного падежей пишется «ь». В конце существительных II склонения после шипящих «ь» не пишется.
Оформите это правило в виде блок-схемы.

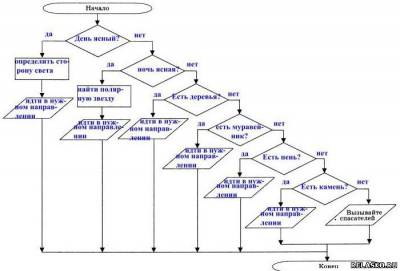
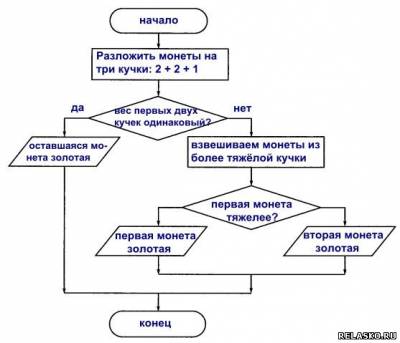
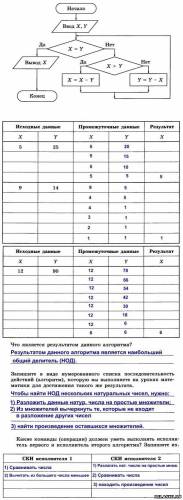
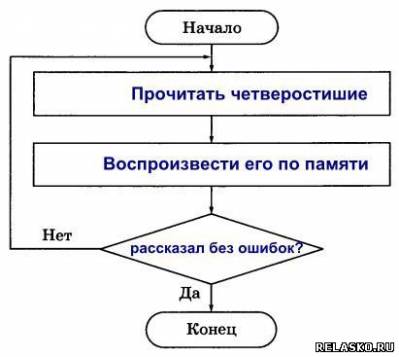
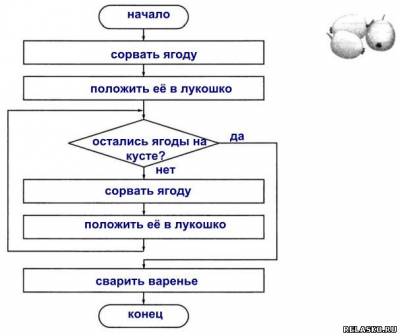
Что бы посмотреть решение и правильный ответ на задачки из рабочей тетради по Информатике Босова нажмите на картинку
196. Для того чтобы успешно ориентироваться на местности, нужно знать следующее:
1) если в ясный полдень стать спиной к солнцу, то впереди будет север, позади — юг, справа — восток, слева — запад;
2) если в ясную полночь найти на небе Полярную звезду, то север будет находиться по направлению к ней;
3) если на местности есть отдельно стоящее дерево, то сторона, с которой его ветви короче, является северной;
4) если на местности есть муравейник, то сторона, с которой он более пологий, является южной;
5) сли на местности есть пень, то сторона, с которой у него годовые кольца шире, является южной;
6) если на местности есть камень, то сторона, с которой он покрыт мхом, является северной.
Оформите данный алгоритм ориентирования на местности в виде блок-схемы.
197. Вспомните русскую народную сказку «Иван Царевич и Серый Волк». Составьте блок-схему для выбора маршрута по надписям на придорожном камне. По какой ветви пошел Иван Царевич?
198. Петя и Коля играют в следующую игру. Петя задумывает натуральное число, не превосходящее 8. Коля должен это число отгадать. Он может задавать Пете вопросы, допускающие только ответы «да» или «нет». Коля старается за наименьшее число вопросов отгадать число, задуманное Петей. Его стратегия основана на делении числового отрезка пополам и выяснении, в какой из половин находится задуманное число.
Пользуясь этой стратегией, внесите недостающие записи в схему.
199. Кот Матроскин и пёс Шарик нашли клад, который состоял из 5 одинаковых монет. В коробке, в которой лежали монеты, друзья обнаружили записку: «При помощи чашечных весов без гирь найдите среди этих 5 монет одну золотую и купите почтальону Печкину велосипед. Сделайте это при помощи двух взвешиваний. Золотая монета более тяжёлая». Дядя Фёдор помог своим друзьям справиться с этим заданием. Как он действовал?
Впишите действия Дяди Фёдора в блок-схему.

Что бы посмотреть решение и правильный ответ на задачки из рабочей тетради по Информатике Босова нажмите на картинку
201. Выполните алгоритм для заданных чисел.
202. Руслан учит наизусть четверостишие, заданное по литературе. Он один раз прочитывает четверостишие и пытается воспроизвести его по памяти. Так он будет делать до тех пор, пока не расскажет четверостишие без единой ошибки.
Запишите действия Руслана в виде блок-схемы.
203. Однажды бабушка попросила Машу помочь собрать ягоды крыжовника. Девочка взяла лукошко и подошла к большому колючему кусту. Она осторожно срывала ягоду и опускала её в лукошко. Так Маша делала до тех пор, пока на кусте не осталось ни одной ягоды. Из этих ягод сварили очень вкусное варенье.
Запишите действия Маши в виде блок-схемы.
204. В узком и очень длинном жёлобе находятся 8 шариков, четыре чёрных слева и четыре белых чуть-чуть большего диаметра справа. В средней части жёлоба в стенке имеется небольшая ниша, в которой может поместиться один чёрный или один белый шарик. Два любых шарика могут расположиться рядом поперек жёлоба только в том месте, где находится ниша. Левый конец жёлоба закрыт, а в правом конце есть отверстие, через которое может пройти чёрный шарик, но не может пройти белый.
Вынимать шарики из жёлоба не разрешается. Как выкатить из жёлоба все чёрные шарики?
205. Коля задумывает натуральное число из отрезка от 1 до N. Петя должен это число отгадать. Он может задавать Коле вопросы, допускающие только ответы «да» или «нет». Петя разработал алгоритм, позволяющий за наименьшее число вопросов отгадать число, задуманное Колей.
206. Исполнитель Вычислитель умеет выполнять только две команды.
Источник
Что будет нарисовано после выполнения чертежником алгоритма 207
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны):
сместиться на (–24, –12)
После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?
Будем считать, что Чертёжник находится в начале координат. После выполнения команды сместиться на (–1, 2) Чертёжник окажется в точке с координатами (–1, 2). После выполнения цикла Чертёжник переместится на где x и y — неизвестные смещения. В результате последнего перемещения Чертёжник должен переместиться в начало координат, то есть:
Поскольку x — целое, из первого уравнения получаем, что n может быть равно 1, 5, 25. Аналогично, из второго уравнения n может быть равно 1, 2, 5, 10. Таким образом, наибольшее число повторений цикла равно 5.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа, n > 1):
сместиться на (30, −10)
сместиться на (−11, −12)
сместиться на (−3, 100)
Укажите наименьшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
После выполнения команд сместиться на (30, –10) и сместиться на (–3, 100) Чертёжник окажется в точке с координатами (27, 90). После выполнения цикла Чертёжник переместится на n · (a − 11, b − 12).
Поскольку требуется, чтобы после выполнения программы Четрёжник вернулся в исходную точку, имеем два уравнения: n · (a − 11) = −27 и n · (b − 12) = −90.
Переменные a, b и n должны быть целыми, причём n > 1. Следовательно, числа −90 и −27 должны быть кратны n. Наименьшее, подходящее n равно 3.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа, n > 1):
сместиться на (30, 30)
сместиться на (15, −9)
сместиться на (2, −10)
Укажите наибольшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
После выполнения команд сместиться на (30, 30) и сместиться на (2, −10) Чертёжник окажется в точке с координатами (32, 20). После выполнения цикла Чертёжник переместится на n · (a + 15, b − 9).
Поскольку требуется, чтобы после выполнения программы Чертёжник вернулся в исходную точку, имеем два уравнения: n · (a + 15) = −32 и n · (b − 9) = −20.
Переменные a, b и n должны быть целыми, причём n > 1. Следовательно, числа −32 и −20 должны быть кратны n. Наибольшее подходящее n равно 4.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны):
сместиться на (−25, −12)
После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?.
Обозначим неизвестное смещение по оси x, по оси y как a и b, неизвестное количество повторений как n.
После выполнения команд сместиться на (5, 2) и (−25, −12) Чертёжник окажется в точке с координатами (−20, −10). После выполнения цикла Чертёжник переместится на n · (a − 1, b − 2).
Поскольку требуется, чтобы после выполнения программы Чертёжник вернулся в исходную точку, имеем два уравнения: n · (a − 1) = −20 и n · (b − 2) = −10.
Переменные a, b и n должны быть целыми, причём n > 1. Следовательно, числа −20 и −10 должны быть кратны n. Наибольшее подходящее n равно 10.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны):
сместиться на (−20, −33)
После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?.
Обозначим неизвестное количество повторений,неизвестное смещение по оси x, по оси y как a, b и c соответственно.
После выполнения команд сместиться на (−1, −2) и (−20, −33) Чертёжник окажется в точке с координатами (−21, −35). После выполнения цикла Чертёжник переместится на n · (a − 1, b − 2).
Поскольку требуется, чтобы после выполнения программы Четрёжник вернулся в исходную точку, имеем два уравнения: n · (a − 1) = −21 и n · (b − 2) = −35.
Переменные a, b и n должны быть целыми, причём n > 1. Следовательно, числа −21 и −35 должны быть кратны n. Наибольшее подходящее n равно 7.
Источник
Что будет нарисовано после выполнения чертежником алгоритма 207
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны):
сместиться на (–24, –12)
После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?
Будем считать, что Чертёжник находится в начале координат. После выполнения команды сместиться на (–1, 2) Чертёжник окажется в точке с координатами (–1, 2). После выполнения цикла Чертёжник переместится на где x и y — неизвестные смещения. В результате последнего перемещения Чертёжник должен переместиться в начало координат, то есть:
Поскольку x — целое, из первого уравнения получаем, что n может быть равно 1, 5, 25. Аналогично, из второго уравнения n может быть равно 1, 2, 5, 10. Таким образом, наибольшее число повторений цикла равно 5.
Источник
Что будет нарисовано после выполнения чертежником алгоритма 207
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a, b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, у) в точку с координатами (x + а, у + b). Если числа a, b положительные, значение соответствующей координаты увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Команда1 Команда2 КомандаЗ
означает, что последовательность команд Команда1 Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Команда1 Сместиться на (3, 2) Сместиться на (2, 1)
После выполнения этого алгоритма Чертёжник вернулся в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−2, −1)
2) Сместиться на (1, 1)
3) Сместиться на (−4, −2)
4) Сместиться на (2, 1)
Команда Повтори 2 раз означает, что команды Сместиться на (3, 2) и Сместиться на (2, 1) выполнятся два раза. В результате Чертёжник переместится на 2·(3 + 2, 2 + 1) = (10, 6). Выполнив последнюю команду Сместиться на (−6, −4), Чертёжник окажется в точке (4, 2).
Чтобы Чертёжник вернулся в исходную точку, необходимо переместить его на (−4, −2). Учитывая, наличие команды Повтори 2 раз, приходим к выводу, что Команда 1 это команда Сместиться на (−2, −1).
Правильный ответ указан под номером 1.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a, b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, у) в точку с координатами (x + а, у + b). Если числа a, b положительные, значение соответствующей координаты увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Команда1 Команда2 КомандаЗ
означает, что последовательность команд Команда1 Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Команда1 Сместиться на (3, 3) Сместиться на (1,−2) Конец
Сместиться на (−8, 12)
После выполнения этого алгоритма Чертёжник вернулся в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−2, −4)
2) Сместиться на (4,−13)
3) Сместиться на (2, 4)
4) Сместиться на (−8, −16)
Команда Повтори 4 раз означает, что команды Сместиться на (3, 3) и Сместиться на (1,−2) выполнются четыре раза. В результате Чертёжник переместится на 4·(3 + 1, 3 − 2) = (16, 4). Выполнив последнюю команду Сместиться на (−8, 12), Чертёжник окажется в точке (8, 16).
Чтобы Чертёжник вернулся в исходную точку, необходимо, переместить его на (−8, −16). Учитывая, наличие команды Повтори 4, приходим к выводу, что Команда 1 это команда Сместиться на (−2, −4).
Правильный ответ указан под номером 1.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a, b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, у) в точку с координатами (x + а, у + b). Если числа a, b положительные, значение соответствующей координаты увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Команда1 Команда2 КомандаЗ
означает, что последовательность команд Команда1 Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Команда1 Сместиться на (1, 3) Сместиться на (1, −2) Конец
После выполнения этого алгоритма Чертёжник вернулся в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (3, 4)
2) Сместиться на (−5, −10)
3) Сместиться на (−9, −12)
4) Сместиться на (−3, −4)
Команда Повтори 3 раз означает, что команды Сместиться на (1, 3) и Сместиться на (1,−2) выполнются три раза. В результате Чертёжник переместится на 3·(1 + 1, 3 − 2) = (6, 3). Выполнив последнюю команду Сместиться на (3, 9), Чертёжник окажется в точке (9, 12).
Чтобы Чертёжник вернулся в исходную точку, необходимо переместить его на (−9, −12). Учитывая, наличие команды Повтори 3, приходим к выводу, что Команда 1 это команда Сместиться на (−3, −4).
Правильный ответ указан под номером 4.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a, b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, у) в точку с координатами (x + а, у + b). Если числа a, b положительные, значение соответствующей координаты увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Команда1 Команда2 КомандаЗ
означает, что последовательность команд Команда1 Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Команда1 Сместиться на (3, 2) Сместиться на (2, 1) Конец
После выполнения этого алгоритма Чертёжник вернулся в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−6, −3)
2) Сместиться на (4, 3)
3) Сместиться на (−2, −1)
4) Сместиться на (2, 1)
Проанализируем алгоритм. Благодаря тому, что присутствует команда Повтори 3, команды Сместиться на (3, 2) Сместиться на (2, 1) выполнятся три раза, в результате чего чертёжник переместится на 3·(3 + 2, 2 + 1) = (15, 9). Выполнив последнюю команду Сместиться на (−9, −6), чертёжник окажется в точке (6, 3).
Для того, чтобы чертёжник вернулся в исходную точку, необходимо, чтобы после выполнения алгоритма его координаты были (0, 0). Учитывая, наличие команды Повтори 3, приходим к выводу, что Команда 1 есть команда Сместиться на (−2, −1).
Источник
Что будет нарисовано после выполнения чертежником алгоритма 207
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a, b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, у) в точку с координатами (x + а, у + b). Если числа a, b положительные, значение соответствующей координаты увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Команда1 Команда2 КомандаЗ
означает, что последовательность команд Команда1 Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Команда1 Сместиться на (3, 2) Сместиться на (2, 1)
После выполнения этого алгоритма Чертёжник вернулся в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−2, −1)
2) Сместиться на (1, 1)
3) Сместиться на (−4, −2)
4) Сместиться на (2, 1)
Команда Повтори 2 раз означает, что команды Сместиться на (3, 2) и Сместиться на (2, 1) выполнятся два раза. В результате Чертёжник переместится на 2·(3 + 2, 2 + 1) = (10, 6). Выполнив последнюю команду Сместиться на (−6, −4), Чертёжник окажется в точке (4, 2).
Чтобы Чертёжник вернулся в исходную точку, необходимо переместить его на (−4, −2). Учитывая, наличие команды Повтори 2 раз, приходим к выводу, что Команда 1 это команда Сместиться на (−2, −1).
Правильный ответ указан под номером 1.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a, b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, у) в точку с координатами (x + а, у + b). Если числа a, b положительные, значение соответствующей координаты увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Команда1 Команда2 КомандаЗ
означает, что последовательность команд Команда1 Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Команда1 Сместиться на (3, 3) Сместиться на (1,−2) Конец
Сместиться на (−8, 12)
После выполнения этого алгоритма Чертёжник вернулся в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−2, −4)
2) Сместиться на (4,−13)
3) Сместиться на (2, 4)
4) Сместиться на (−8, −16)
Команда Повтори 4 раз означает, что команды Сместиться на (3, 3) и Сместиться на (1,−2) выполнются четыре раза. В результате Чертёжник переместится на 4·(3 + 1, 3 − 2) = (16, 4). Выполнив последнюю команду Сместиться на (−8, 12), Чертёжник окажется в точке (8, 16).
Чтобы Чертёжник вернулся в исходную точку, необходимо, переместить его на (−8, −16). Учитывая, наличие команды Повтори 4, приходим к выводу, что Команда 1 это команда Сместиться на (−2, −4).
Правильный ответ указан под номером 1.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a, b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, у) в точку с координатами (x + а, у + b). Если числа a, b положительные, значение соответствующей координаты увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Команда1 Команда2 КомандаЗ
означает, что последовательность команд Команда1 Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Команда1 Сместиться на (1, 3) Сместиться на (1, −2) Конец
После выполнения этого алгоритма Чертёжник вернулся в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (3, 4)
2) Сместиться на (−5, −10)
3) Сместиться на (−9, −12)
4) Сместиться на (−3, −4)
Команда Повтори 3 раз означает, что команды Сместиться на (1, 3) и Сместиться на (1,−2) выполнются три раза. В результате Чертёжник переместится на 3·(1 + 1, 3 − 2) = (6, 3). Выполнив последнюю команду Сместиться на (3, 9), Чертёжник окажется в точке (9, 12).
Чтобы Чертёжник вернулся в исходную точку, необходимо переместить его на (−9, −12). Учитывая, наличие команды Повтори 3, приходим к выводу, что Команда 1 это команда Сместиться на (−3, −4).
Правильный ответ указан под номером 4.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a, b) (где a, b — целые числа), перемещающую Чертёжника из точки с координатами (x, у) в точку с координатами (x + а, у + b). Если числа a, b положительные, значение соответствующей координаты увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4, 2), то команда Сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Команда1 Команда2 КомандаЗ
означает, что последовательность команд Команда1 Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Команда1 Сместиться на (3, 2) Сместиться на (2, 1) Конец
После выполнения этого алгоритма Чертёжник вернулся в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−6, −3)
2) Сместиться на (4, 3)
3) Сместиться на (−2, −1)
4) Сместиться на (2, 1)
Проанализируем алгоритм. Благодаря тому, что присутствует команда Повтори 3, команды Сместиться на (3, 2) Сместиться на (2, 1) выполнятся три раза, в результате чего чертёжник переместится на 3·(3 + 2, 2 + 1) = (15, 9). Выполнив последнюю команду Сместиться на (−9, −6), чертёжник окажется в точке (6, 3).
Для того, чтобы чертёжник вернулся в исходную точку, необходимо, чтобы после выполнения алгоритма его координаты были (0, 0). Учитывая, наличие команды Повтори 3, приходим к выводу, что Команда 1 есть команда Сместиться на (−2, −1).
Источник
← Что будет написано на лбу даджаля
Что будет нарисовано после выполнения чертежником алгоритма поднять перо 5 4 →
Вам также понравится
Что будет если поймают на скутере без прав и документов
11.07.202211.07.2022 admin 0
декоративная штукатурка под травертин для фасада
09.07.202208.07.2022 admin 0
что значит фиксированная ставка по вкладу
14.07.202215.07.2022 admin 0
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.

Стоимость криптовалют сегодня:
Я тебя обыграю! Спорим?
Ваш ход

Текущая дата:
Найти на сайте

Свежие записи
Книгу Звездная Кровь – 7. Дикая Охота автора Роман Прокофьев вы можете прочитать бесплатно на сайте pedagogik-a.ru в хорошем качестве или скачать в виде FB2, TXT, PDF, EPUB.
Книгу Антидемон. Книга 14 автора Серж Винтеркей вы можете прочитать бесплатно на сайте pedagogik-a.ru в хорошем качестве или скачать в виде FB2, TXT, PDF, EPUB.
Книгу Форсайт автора Сергей Лукьяненко вы можете прочитать бесплатно на сайте pedagogik-a.ru в хорошем качестве или скачать в виде FB2, TXT, PDF, EPUB.
Книгу Убийства и кексики. Детективное агентство «Благотворительный магазин» автора Питер Боланд, Анастасия Осминина, INSPIRIA вы можете прочитать бесплатно на сайте pedagogik-a.ru в хорошем качестве или скачать в виде FB2, TXT, PDF, EPUB.
Книгу Совершенные автора Марина Суржевская вы можете прочитать бесплатно на сайте pedagogik-a.ru в хорошем качестве или скачать в виде FB2, TXT, PDF, EPUB.
Свежие комментарии
sima к записи Izotope что это за программа и нужна ли она
Александр к записи indigo что это за программа
Александр к записи где взять puk код yota
фахриддин к записи где взять puk код yota
Александр к записи snapbizcard что это за программа
Контакты для Роскомнадзора - informationforweb2023@gmail.com
Все права сохранены. © 2025 Что и как устроено в мире? Внимание! Информация, опубликованная на сайте, носит исключительно ознакомительный характер и не является рекомендацией к применению. Материалы могут содержать информацию, предназначенную для пользователей старше 18 лет. 18+.