Что будет нарисовано после выполнения чертежником алгоритма поднять перо 5 4
Исполнитель Чертежник. Пример алгоритма управления Чертежником. Работа в среде исполнителя Чертежник
Исполнитель Чертежник. Пример алгоритма управления Чертежником. Работа в среде исполнителя Чертежник
Планируемые результаты освоения обучающимися темы:
предметные – умения разработки алгоритмов для управления исполнителем;
метапредметные – умения самостоятельно планировать пути достижения целей; соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности, определять способы действий в рамках предложенных условий, корректировать свои действия в соответствии с изменяющейся ситуацией; оценивать правильность выполнения учебной задачи; умение разбивать задачу на подзадачи; опыт принятия решений и управления исполнителями с помощью составленных для них алгоритмов;
личностные – способность увязать учебное содержание с собственным жизненным опытом, понять значение развитого алгоритмического мышления для современного человека
Основные виды деятельности обучающихся:
регулятивные: целеполагание как постановка учебной задачи; планирование; прогнозирование; контроль; коррекция; оценка; способность к волевому усилию;
познавательные: знаково-символические действия; моделирование; структурировать знания; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности; формулирование проблемы; самостоятельное создание способов решения проблем творческого и поискового характера
коммуникативные : определять наиболее рациональную последовательность действий по коллективному выполнению учебной задачи; самостоятельно оценивать свою деятельность и деятельность членов коллектива;
Оборудование: компьютер, учебник, тетрадь, приложение.
Приветствие, проверка присутствующих. Запись темы урока в тетрадь и сообщение целей урока.
II.Инструктаж по Технике безопасности.
I II .Актуализация материала.
IV .Изучение нового материала.
Что будет нарисовано после выполнения Чертёжником алго ритма?
1) использовать Чертежник
Задание 2
Составьте для Чертёжника алгоритм рисования прямоугольника со сторонами, параллельными осям координат, если известны координаты его двух вершин: (2, 1) и (7, 5).
Решение
сместиться в точку (2, 1)
опустить перо
сместиться в точку (2, 5)
сместиться в точку (7, 5)
сместиться в точку (7, 1)
сместиться в точку (2, 1)
Задание 5
Составьте алгоритм рисования изображенных ниже фигур так, чтобы в процессе рисования перо не отрывалось от бумаги и ни одна линия не проводилась дважды. 
Решение
а) опустить перо
сместиться в точку (0, 4)
сместиться в точку (4, 4)
сместиться в точку (0, 0)
сместиться в точку (4, 0)
сместиться в точку (4, 4)
сместиться в точку (8, 4)
сместиться в точку (4, 0)
сместиться в точку (8, 0)
сместиться в точку (8, 4)
б) сместиться в точку (2, 2)
опустить перо
сместиться в точку (0, 2)
сместиться в точку (0, 6)
сместиться в точку (4, 6)
сместиться в точку (4, 2)
сместиться в точку (2, 2)
сместиться в точку (2, 4)
сместиться в точку (6, 4)
сместиться в точку (6, 0)
сместиться в точку (2, 0)
сместиться в точку (2, 2)
в) сместиться в точку (1, 0)
опустить перо
сместиться в точку (4, 6)
сместиться в точку (7, 0)
сместиться в точку (0, 4)
сместиться в точку (8, 4)
сместиться в точку (1, 0)
Задание 6
Оформите вспомогательные алгоритмы для рисования букв «М», «И», «Р». Составьте алгоритмы рисования слов «МИР», «РИМ», «МИМ». 
Решение
АЛГОРИТМ СЛОВА МИР
использовать Чертежник
алг слово МИР
нач
буква_М
буква_И
буква_Р
кон
АЛГОРИТМ СЛОВА РИМ
использовать Чертежник
алг слово РИМ
нач
буква_Р
буква_И
буква_М
кон
АЛГОРИТМ СЛОВА МИМ
использовать Чертежник
алг слово МИМ
нач
буква_М
буква_И
буква_М
кон
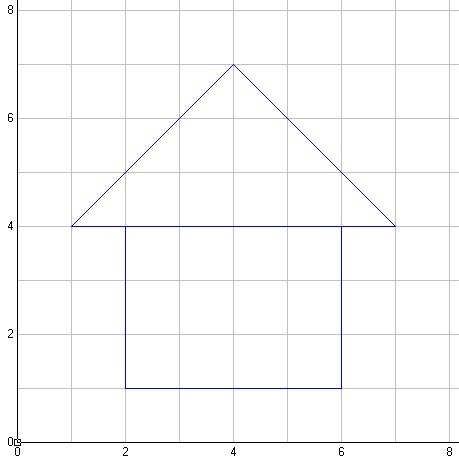
АЛГОРИТМ РИСОВАНИЯ 5 ДОМОВ
использовать Чертежник
алг ряд домов нач
сместиться в точку (1, 3)
нц 5 раз
опустить перо
дом
поднять перо
сместиться на вектор (2, 1)
кц
кон
Задание 8
Составьте алгоритмы управления Чертёжником, после исполнения которых будут получены следующие рисунки: 
Решение
а) алг квадрат_1
нач
опустить перо
сместиться в точку (6, 0)
сместиться в точку (6, 6)
сместиться в точку (0, 6)
сместиться в точку (0, 0)
поднять перо
кон
поднять перо
сместиться на вектор (0, 1)
опустить перо
сместиться на вектор (1, 0)
поднять перо
сместиться на вектор (- 4, 0)
опустить перо
сместиться на вектор (1, 0)
Что будет нарисовано после выполнения чертежником алгоритма поднять перо 5 4
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны):
сместиться на (–24, –12)
После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?
Будем считать, что Чертёжник находится в начале координат. После выполнения команды сместиться на (–1, 2) Чертёжник окажется в точке с координатами (–1, 2). После выполнения цикла Чертёжник переместится на где x и y — неизвестные смещения. В результате последнего перемещения Чертёжник должен переместиться в начало координат, то есть:
Поскольку x — целое, из первого уравнения получаем, что n может быть равно 1, 5, 25. Аналогично, из второго уравнения n может быть равно 1, 2, 5, 10. Таким образом, наибольшее число повторений цикла равно 5.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа, n > 1):
сместиться на (30, −10)
сместиться на (−11, −12)
сместиться на (−3, 100)
Укажите наименьшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
После выполнения команд сместиться на (30, –10) и сместиться на (–3, 100) Чертёжник окажется в точке с координатами (27, 90). После выполнения цикла Чертёжник переместится на n · (a − 11, b − 12).
Поскольку требуется, чтобы после выполнения программы Четрёжник вернулся в исходную точку, имеем два уравнения: n · (a − 11) = −27 и n · (b − 12) = −90.
Переменные a, b и n должны быть целыми, причём n > 1. Следовательно, числа −90 и −27 должны быть кратны n. Наименьшее, подходящее n равно 3.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа, n > 1):
сместиться на (30, 30)
сместиться на (15, −9)
сместиться на (2, −10)
Укажите наибольшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
После выполнения команд сместиться на (30, 30) и сместиться на (2, −10) Чертёжник окажется в точке с координатами (32, 20). После выполнения цикла Чертёжник переместится на n · (a + 15, b − 9).
Поскольку требуется, чтобы после выполнения программы Чертёжник вернулся в исходную точку, имеем два уравнения: n · (a + 15) = −32 и n · (b − 9) = −20.
Переменные a, b и n должны быть целыми, причём n > 1. Следовательно, числа −32 и −20 должны быть кратны n. Наибольшее подходящее n равно 4.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны):
сместиться на (−25, −12)
После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?.
Обозначим неизвестное смещение по оси x, по оси y как a и b, неизвестное количество повторений как n.
После выполнения команд сместиться на (5, 2) и (−25, −12) Чертёжник окажется в точке с координатами (−20, −10). После выполнения цикла Чертёжник переместится на n · (a − 1, b − 2).
Поскольку требуется, чтобы после выполнения программы Чертёжник вернулся в исходную точку, имеем два уравнения: n · (a − 1) = −20 и n · (b − 2) = −10.
Переменные a, b и n должны быть целыми, причём n > 1. Следовательно, числа −20 и −10 должны быть кратны n. Наибольшее подходящее n равно 10.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны):
сместиться на (−20, −33)
После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?.
Обозначим неизвестное количество повторений,неизвестное смещение по оси x, по оси y как a, b и c соответственно.
После выполнения команд сместиться на (−1, −2) и (−20, −33) Чертёжник окажется в точке с координатами (−21, −35). После выполнения цикла Чертёжник переместится на n · (a − 1, b − 2).
Поскольку требуется, чтобы после выполнения программы Четрёжник вернулся в исходную точку, имеем два уравнения: n · (a − 1) = −21 и n · (b − 2) = −35.
Переменные a, b и n должны быть целыми, причём n > 1. Следовательно, числа −21 и −35 должны быть кратны n. Наибольшее подходящее n равно 7.
Что будет нарисовано после выполнения Чертежником алгоритма: Поднять перо Сместиться в точку 2.4 Опустить перо Сместить на векто
Решение показано в прилагаемом файле.
Формулы:
Для столбца H:
Сумма: =СУММ(C2:G2)
Количество мастеров спорта: =СЧЁТЕСЛИ(H2:H11;»>=150″)
Max =: =МАКС(H2:H11)
Мин =: =МИН(H2:H11)
Для столбца I:
Среднее: =СРЗНАЧ(C2:G2)
ФИО спортсмена с макс. баллами:
=ИНДЕКС(A2:H11;ПОИСКПОЗ(H13;H2:H11;0);2)
ФИО спортсмена с мин. баллами:
=ИНДЕКС(A2:H11;ПОИСКПОЗ(H14;H2:H11;0);2)
золотое правило этики гласит «поступайте с другими так, как хоте ли бы, чтобы поступали с вами», пословицы:
худой мир лучше доброй ссоры
кто старое помянет, тому глаз вон
не руби сук, на котором сидишь
не плюй в колодец, пригодится воды напиться
вражда не делает добра
доброе слово лечит, а злое убивает
доброе слово и кошке приятно
+
1)Можешь позвонить друзьям в любую минуту
2)У тебя всегда есть как провести досуг, ведь в смартфоне есть игры
3)Ты можешь слушать любую музыку, если есть интернет
4)Теперь не нужна большая фотокамера, чтобы запечатлеть интересные моменты в твоей жизни
5)Твоя личная, персональная информация теперь всегда может быть с тобой
Что будет нарисовано после выполнения чертежником алгоритма поднять перо 5 4
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны):
сместиться на (–24, –12)
После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?
Будем считать, что Чертёжник находится в начале координат. После выполнения команды сместиться на (–1, 2) Чертёжник окажется в точке с координатами (–1, 2). После выполнения цикла Чертёжник переместится на где x и y — неизвестные смещения. В результате последнего перемещения Чертёжник должен переместиться в начало координат, то есть:
Поскольку x — целое, из первого уравнения получаем, что n может быть равно 1, 5, 25. Аналогично, из второго уравнения n может быть равно 1, 2, 5, 10. Таким образом, наибольшее число повторений цикла равно 5.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа, n > 1):
сместиться на (30, −10)
сместиться на (−11, −12)
сместиться на (−3, 100)
Укажите наименьшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
После выполнения команд сместиться на (30, –10) и сместиться на (–3, 100) Чертёжник окажется в точке с координатами (27, 90). После выполнения цикла Чертёжник переместится на n · (a − 11, b − 12).
Поскольку требуется, чтобы после выполнения программы Четрёжник вернулся в исходную точку, имеем два уравнения: n · (a − 11) = −27 и n · (b − 12) = −90.
Переменные a, b и n должны быть целыми, причём n > 1. Следовательно, числа −90 и −27 должны быть кратны n. Наименьшее, подходящее n равно 3.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа, n > 1):
сместиться на (30, 30)
сместиться на (15, −9)
сместиться на (2, −10)
Укажите наибольшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
После выполнения команд сместиться на (30, 30) и сместиться на (2, −10) Чертёжник окажется в точке с координатами (32, 20). После выполнения цикла Чертёжник переместится на n · (a + 15, b − 9).
Поскольку требуется, чтобы после выполнения программы Чертёжник вернулся в исходную точку, имеем два уравнения: n · (a + 15) = −32 и n · (b − 9) = −20.
Переменные a, b и n должны быть целыми, причём n > 1. Следовательно, числа −32 и −20 должны быть кратны n. Наибольшее подходящее n равно 4.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны):
сместиться на (−25, −12)
После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?.
Обозначим неизвестное смещение по оси x, по оси y как a и b, неизвестное количество повторений как n.
После выполнения команд сместиться на (5, 2) и (−25, −12) Чертёжник окажется в точке с координатами (−20, −10). После выполнения цикла Чертёжник переместится на n · (a − 1, b − 2).
Поскольку требуется, чтобы после выполнения программы Чертёжник вернулся в исходную точку, имеем два уравнения: n · (a − 1) = −20 и n · (b − 2) = −10.
Переменные a, b и n должны быть целыми, причём n > 1. Следовательно, числа −20 и −10 должны быть кратны n. Наибольшее подходящее n равно 10.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и смещения в первой из повторяемых команд неизвестны):
сместиться на (−20, −33)
После выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?.
Обозначим неизвестное количество повторений,неизвестное смещение по оси x, по оси y как a, b и c соответственно.
После выполнения команд сместиться на (−1, −2) и (−20, −33) Чертёжник окажется в точке с координатами (−21, −35). После выполнения цикла Чертёжник переместится на n · (a − 1, b − 2).
Поскольку требуется, чтобы после выполнения программы Четрёжник вернулся в исходную точку, имеем два уравнения: n · (a − 1) = −21 и n · (b − 2) = −35.
Переменные a, b и n должны быть целыми, причём n > 1. Следовательно, числа −21 и −35 должны быть кратны n. Наибольшее подходящее n равно 7.