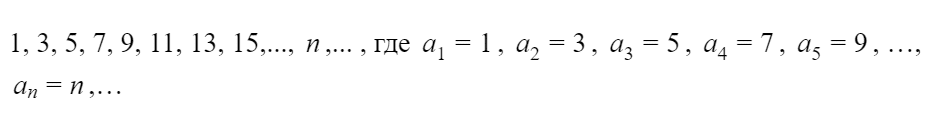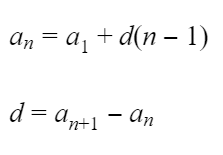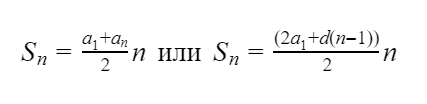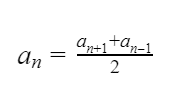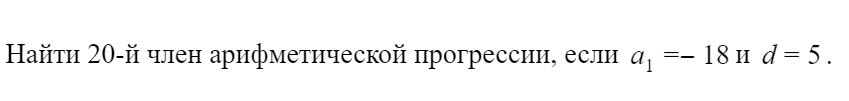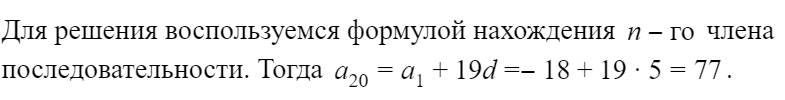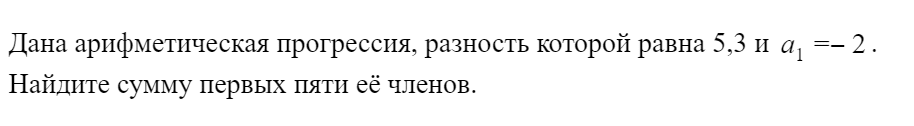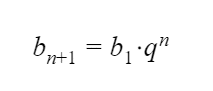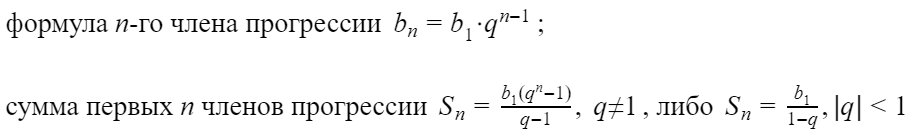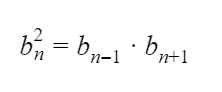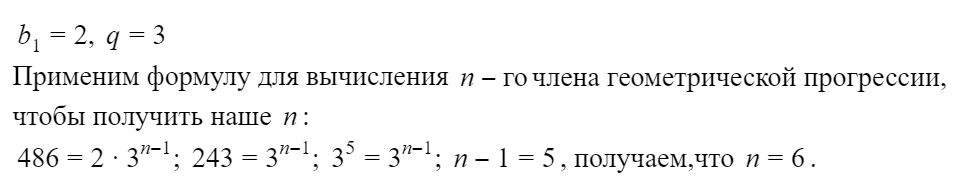Что быстрее геометрическая прогрессия или арифметическая
Прогрессии и последовательности: решаем ОГЭ по математике
Григорий Грянников
Тема «прогрессии» на ОГЭ тесно связана с понятием «последовательность». Если ученики понимают, как числа в последовательности связаны друг с другом, они легко справляются с заданиями. Сейчас мы разберем прогрессии — одну из самых коварных тем ОГЭ по математике. Обратите внимание: в этом материале все самое главное для решения ОГЭ, никакой воды!
Что такое последовательность?
В жизни мы очень часто сталкиваемся с математическими последовательностями и прогрессиями, буквально, каждый день, сами того не замечая. Однако встреча не всегда может быть приятной, особенно если она происходит на экзамене.
Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:
Хочешь круто подготовится к ОГЭ? Тебе поможет учебный центр MAXIMUM! Все наши преподаватели сами сдавали этот экзамен на хороший балл. Мы ежегодно изучаем изменения ФИПИ и корректируем курсы, исходя из этого. Читай подробнее про наши курсы и выбирай подходящий!
Какие виды последовательности бывают?
Различают следующие виды последовательности:
Что такое арифметическая прогрессия?
Давайте посмотрим на следующий ряд чисел:
Что же у них может быть общего? Во-первых, все они нечетные, во-вторых, каждое следующее число мы можем получить из предыдущего, прибавляя к нему одно и то же число. Назовем это число d. В нашем случае d=2.
Описанная выше последовательность называется арифметической прогрессией. Получаем определение:
Приведем основные формулы:
Сумма первых n членов прогрессии можно вычислить по формуле:
Также арифметическая прогрессия обладает характерным свойством:
Как решать задачи ОГЭ на арифметическую прогрессию?
Теория — это прекрасно, но каждую теоретическую тему необходимо закреплять на практике. Сейчас мы разберем пару заданий ОГЭ по арифметической прогрессии.
Например, на ОГЭ может попасться вот такое задание:
Решение:
Ура! Первый прототип задания, который может встретиться на реальном экзамене, успешно выполнен. Идем дальше.
Решение:
Вот и все! Ничего сложного, учитывая то, что формула суммы первых n членов прогрессии есть в справочных материалах, которые выдаются на экзамене.
Что такое геометрическая прогрессия?
Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q – знаменатель прогрессии. Элементы геометрической прогрессии можно задать соотношением:
Вот основные формулы для геометрической прогрессии:
Также геометрическая прогрессия, как и арифметическая, обладает характерным свойством:
Как решать задачи ОГЭ на геометрическую прогрессию?
Закрепим материал на практике и разберем две задачи ОГЭ по геометрической прогрессии.
Как видите, со знанием формул любое задание становится несложным!
В каком задании ОГЭ могут встретиться прогрессии?
Тема «Прогрессия» встречается в задании ОГЭ под номером 12. Выполнение этого задания экзаменуемым зависит от уровня сложности самого задания. В среднем с ним справляется всего 47% школьников. Как видите, сама тема не очень сложная. Все можно решить — достаточно правильно и хорошо подготовиться.
Напомним, что в КИМах с инструкцией и заданиями есть вспомогательные формулы, которые помогут при решении нашей задачи на прогрессию.
Теперь вы знаете теорию по теме прогрессии на ОГЭ. Можете смело оттачивать знания на практике. Пусть ваша встреча с прогрессиями на экзамене будет не печальной, а победной!
Хотите разобраться в других темах ОГЭ? Боитесь, что экзамены уже в следующем году, а вы даже не открывали учебники? Начните готовиться к ОГЭ-2021 уже сейчас на курсах с MAXIMUM. Мы поможем закрыть пробелы и сдать все на отлично. Правильная и интересная подготовка — залог успеха на экзаменах. Консультация бесплатно!
math4school.ru
Арифметическая и геометрическая прогрессии
Числовые последовательности (основные понятия)
Если каждому натуральному числу n поставить в соответствие действительное число an , то говорят, что задано числовую последовательность :
Итак, числовая последовательность — функция натурального аргумента.
Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.
последовательность положительных нечётных чисел можно задать формулой
а последовательность чередующихся 1 и –1 — формулой
Последовательность можно определить рекуррентной формулой, то есть формулой, которая выражает любой член последовательности, начиная с некоторого, через предыдущие (один или несколько) члены.
последовательность двузначных натуральных чисел:
Последовательность простых чисел:
Монотонными последовательностями, в частности, являются возрастающие последовательности и убывающие последовательности.
Арифметическая прогрессия
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, к которому прибавляется одно и то же число.
является арифметической прогрессией, если для любого натурального числа n выполняется условие:
где d — некоторое число.
Таким образом, разность между последующим и предыдущим членами данной арифметической прогрессии всегда постоянна:
Чтобы задать арифметическую прогрессию, достаточно указать её первый член и разность.
найдём тридцатый член арифметической прогрессии
| an = | an–1 + an+1 |
| 2 |
каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.
Так как верно и обратное утверждение, то имеет место следующее утверждение:
числа a, b и c являются последовательными членами некоторой арифметической прогрессии тогда и только тогда, когда одно из них равно среднему арифметическому двух других.
Воспользуемся приведённым выше утверждением. Имеем:
| an+1 + an–1 | = | 2n – 5 + 2n – 9 | = 2n – 7 = an, |
| 2 | 2 |
что и доказывает нужное утверждение. ◄
| an = | a n–k + a n+k |
| 2 |
любой член арифметической прогрессии, начиная со второго равен полусумме равноотстоящих от него членов этой арифметической прогрессии.
Кроме того, для любой арифметической прогрессии справедливо равенство:
первых n членов арифметической прогрессии равна произведению полусуммы крайних слагаемых на число слагаемых:
Отсюда, в частности, следует, что если нужно просуммировать члены
то предыдущая формула сохраняет свою структуру:
Если дана арифметическая прогрессия, то величины a1, an, d, n и S n связаны двумя формулами:
| an = a1 + (n – 1)d и Sn = | a1 + an | · n . |
| 2 |
Поэтому, если значения трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.
Арифметическая прогрессия является монотонной последовательностью. При этом:
Геометрическая прогрессия
Геометрической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.
является геометрической прогрессией, если для любого натурального числа n выполняется условие:
где q ≠ 0 — некоторое число.
Таким образом, отношение последующего члена данной геометрической прогрессии к предыдущему есть число постоянное:
Чтобы задать геометрическую прогрессию, достаточно указать её первый член и знаменатель.
каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому (пропорциональному) предшествующего и последующего членов.
Так как верно и обратное утверждение, то имеет место следующее утверждение:
числа a, b и c являются последовательными членами некоторой геометрической прогрессии тогда и только тогда, когда квадрат одного из них равен произведению двух других, то есть одно из чисел является средним геометрическим двух других.
что и доказывает нужное утверждение. ◄
квадрат любого члена геометрической прогрессии, начиная со второго равен произведению равноотстоящих от него членов этой прогрессии.
Кроме того, для любой геометрической прогрессии справедливо равенство:
первых n членов геометрической прогрессии со знаменателем q ≠ 0 вычисляется по формуле:
| Sn = b1 · | 1 – q n | . |
| 1 – q |
А при q = 1 — по формуле
Заметим, что если нужно просуммировать члены
то используется формула:
Если дана геометрическая прогрессия, то величины b1, bn, q, n и Sn связаны двумя формулами:
| bn = b1 · q n –1 и Sn = b1 · | 1 – q n | . |
| 1 – q |
Поэтому, если значения каких-либо трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.
Для геометрической прогрессии с первым членом b1 и знаменателем q имеют место следующие свойства монотонности :
Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:
Бесконечно убывающая геометрическая прогрессия
Заметим, что бесконечно убывающая геометрическая прогрессия может не быть убывающей последовательностью. Это соответствует случаю
При таком знаменателе последовательность знакопеременная. Например,
Связь арифметической и геометрической прогрессий
Арифметическая и геометрическая прогрессии тесно связаны между собой. Рассмотрим лишь два примера.
Сравнение арифметической и геометрической прогрессий.
Презентация дает возможность увидеть различия между арифметической и геометрической прогрессиями на примерах и графиках.
Просмотр содержимого документа
«Сравнение арифметической и геометрической прогрессий.»
Гимназия №148 имени Сервантеса
Сравнение арифметической и геометрической прогрессий
Учитель Киреева В.И.
Техническая поддержка Бутман А. С.
Данная презентация предназначена для поддержки учебного процесса. Она одновременно является источником информации и средством привлечения внимания.
Каждый слайд рассматривается как продолжение предыдущего. Учитель имеет возможность проиллюстрировать с помощью презентации сходства и различия арифметической и геометрической прогрессий на достаточном количестве примеров, вывести характеристические свойства обеих прогрессий, показать на графиках скорость роста каждой из них.
Данная презентация может быть использована для самостоятельного изучения темы.
Рабочий выложил плитку следующим образом: в первый ряд он положил 3 плитки, во второй 5, и так далее, увеличивая каждый ряд на 2 плитки. Сколько плиток в 7 ряду?
В благоприятных условиях бактерии размножаются так, что за одну минуту каждая делится на две. Указать количество бактерий, рожденных одной бактерией за 7 минут.
Сравните между собой последовательности,
по общим свойствам разделите их на группы
Каждый следующий член последовательности получается прибавлением к предыдущему одного и того же числа.
Каждый следующий член последовательности получается из предыдущего умножением на одно и тоже число.
последовательность чисел, отличных от нуля, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число, не равное нулю.
Арифметическая и геометрическая прогрессии
Разделы: Математика
Геометрическая прогрессия.
I. Легенда о шахматах.
Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен её остроумием и разнообразием возможных в ней положений. Узнав, что она изобретена одним из его подданных, он приказал привести его, чтобы лично наградить за удачную выдумку.
Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.
– Я желаю достойно наградить вознаградить тебя за прекрасную игру, которую ты придумал – сказал царь.
– Я достаточно богат, чтобы исполнить самое смелое твое пожелание, – продолжал царь. – Назови награду, которая тебя удовлетворит, и ты получишь её.
– Не робей, – ободрил его царь. – Выскажи свое желание. Я не пожалею ничего, чтобы исполнить его.
– Велика доброта твоя, повелитель. Но дай срок обдумать ответ. Завтра, по зрелом размышлении, я сообщу тебе мою просьбу.
Когда на следующий день Сета снова явился к ступеням трона, он удивил царя беспримерной скромностью своей просьбы.
– Повелитель, – сказал Сета, – прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
– Простое пшеничное зерно? – изумился царь.
– Да, повелитель. За вторую клетку прикажи выдать 2 зерна, за третью – 4, за четвертую – 8, за пятую – 16, за шестую – 32…
– Довольно, – с раздражением прервал его царь. – Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше предыдущей. Но знай, что просьба твоя не достойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моей милостью. Поистине, как учитель ты мог бы показать лучший пример уважения к доброте своего государя. Ступай. Слуги мои вынесут тебе твой мешок с пшеницей.
Сета улыбнулся, покинул залу и стал дожидаться у ворот дворца.
За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли уже безрассудный Сета свою жалкую награду.
– Повелитель, – был ответ, – приказание твое исполняется. Придворные математики исчисляют число следуемых зерен.
Царь нахмурился. Он не привык, чтобы повеления его исполнялись так медлительно. Вечером, отходя ко сну, царь ещё раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.
– Повелитель, – ответили ему, – математики твои трудятся без устали и надеются ещё до рассвета закончить подсчет.
– Почему медлят с этим делом? – гневно воскликнул царь. – Завтра, прежде чем я проснусь, все до последнего зерна должно быть выдано Сете. Я дважды не приказываю.
Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение. Царь приказал ввести его.
– Прежде чем скажешь о твоем деле, – объявил Шерам, – я желаю услышать, выдана ли, наконец, Сете та ничтожная награда, которую он себе назначил.
– Ради этого я и осмелился явиться перед тобой в столь ранний час, – ответил старик. – Мы добросовестно исчислили всё количество зерен, которое желает получить Сета. Число это так велико…
– Как бы велико оно не было – надменно перебил царь, – житницы мои не оскудеют. Награда обещана и должна быть выдана.
– Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерён, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зёрен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыни. Пусть все пространство их сплошь будет засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду.
С изумлением царь внимал словам старца.
– Назови же мне это чудовищное число, – сказал он в раздумье.
– 18 квинтильонов 446 квадрильонов 744 трилионна 073 биллиона 709 миллионов 551 тысяча 615, о, повелитель!
Другой знаменитой задачей на геометрическую прогрессию является задача, известная еще в Древнем Египте, появившаяся в русском фольклоре в следующем виде:
“Шли семь старцев,
У каждого старца
По семи костылей,
На каждом костыле
По семи сучков,
На каждом сучке
По семи кошелей,
В каждом кошеле
По семи пирогов,
А в каждом пироге
По семи воробьев.
Сколько всего?”
Практическое применение геометрической прогрессии.
1. Вероятно, первая ситуация, в которой людям пришлось столкнуться с геометрической прогрессией – подсчет численности стада, проведенный несколько раз, через равные промежутки времени. Если не происходит никаких чрезвычайных ситуаций, количество новорожденных и умерших животных пропорционально числу всех животных. Значит, если за какой-то период времени количество овец у пастуха увеличилось с 10 голов до 20, то за следующий такой же период оно снова вырастит вдвое и станет равным 40.
2. В жизненной практике геометрическая прогрессия появляется в первую очередь в задаче об исчислении так называемых “сложных процентов”. Если положить деньги на срочный вклад в сберегательный банк, то через год вклад увеличится на 3% от исходной суммы, т.е. новая сумма будет равна вкладу, умноженному на 1,03. Ещё через год уже эта сумма увеличится на 3%, т.е. вновь умножится на 1,03. За 20 лет сумма на сберкнижке увеличится в (1,03) 20 
Если процент будет больше, то и результат будет резко расти. Так при 50% годовом увеличении за 10 лет сумма увеличится в (1,5) 10 
3. Еще один пример геометрической прогрессии – изменение массы радиоактивного вещества со временем. Известно, что за единицу времени такое вещество теряет определенную часть своей массы (она переходит в другое вещество и энергию). Для каждого радиоактивного вещества определяется величина T – время периода полураспада. Массы нераспавшегося вещества в моменты 0, T, 2T, 3T,… будут образовывать бесконечно убывающую геометрическую прогрессию.
4. Прирост древесины в лесном массиве происходит по законам геометрической прогрессии. При этом у каждой породы дерева свой коэффициент годового роста объема. Учет этих изменений позволяет планировать вырубку части лесных массивов и одновременную работу по восстановлению лесов.
5. В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две.
6. Английский экономист епископ Мальтус использовал геометрическую и арифметическую прогрессии для оправдания войн: средства потребления (пища, одежда) растут по законам арифметической прогрессии, а люди размножаются по законам геометрической прогрессии. Чтоб избавиться от лишнего населения необходимы войны.
Почему геометрическая прогрессия названа “геометрической”? Видимо потому, что каждый её член равен среднему геометрическому, соседних с ним членов.
А такое среднее названо геометрическим, поскольку оно является стороной квадрата, равновеликого прямоугольнику, стороны которого имеют длины, равные тем величинам, от которых берется среднее.
Геометрические прогрессии удивляют своим чрезвычайно быстрым ростом. В жизни с растущими геометрическими прогрессиями надо обращаться осторожно. Если в геометрической прогрессии растет количество животных в стаде – скоро ему не хватит пастбища. Если число распадов в куче плутония – дело идет к атомному взрыву. А если вам обещают большие доходы – лучше не связываться с этими “благодетелями”.
Арифметическая прогрессия.
При изучении данной темы предлагается использовать ряд нестандартных задач, а также задач с практическим содержанием и совершить небольшой экскурс в историю.
1. Представьте, что вы учетчик на стройке. Привезли и выгрузили большое количество бревен строевого леса. Нужно быстро определить, сколько бревен привезли, чтобы закрыть наряд шоферу.
2. Известна интересная история о знаменитом немецком математике К. Гауссе (1777 – 1855), который еще в детстве обнаружил выдающиеся способности к математике. Учитель предложил учащимся сложить все натуральные числа от 1 до 100. Маленький Гаусс решил эту задачу за одну минуту, сообразив, что суммы 1+100, 2+99 и т.д равны, он умножил 101 на 50, т.е. на число таких сумм. Иначе говоря, он заметил закономерность, присущую арифметическим прогрессиям.
Задача очень непроста:
Как сделать, чтобы быстро
От единицы и до ста
Сложить в уме все числа?
Пять первых связок изучи.
Найдешь к решению ключи!
1+100? 2+99? 3+98?
4+97? 5+96?
Давным-давно один мудрец сказал,
Что прежде надо
Связать начало и конец
У численного ряда.
3. Представители точных наук во всем ищут математические закономерности и учат этому на своих уроках детей. Одна из форм демонстрации математических закономерностей – это математические фокусы. Например, фокусы с календарями.
Фокус 1. Таинственные квадраты.
На помесячном табель – календаре выберите любой месяц, отметьте на нем квадрат, содержащий 9 чисел. Теперь назовите наименьшее из них, а я объявлю сумму всех девяти чисел.
Ответ: (m+8)*9; (m – наименьшее число).
Фокус 2. Предсказание.
На каком-нибудь листе помесячного календаря заключите в квадрат 16 чисел. Разрешите мне мельком взглянуть на ваши квадраты (предсказать число).
Обведите кружком любое число из этого квадрата. Затем зачеркните все числа, стоящие в той же строке и том же столбце, что и обведенное число. В качестве второго обведите любое число, оставшееся не зачеркнутым. Затем зачеркните все числа, оказавшиеся на одной строке и одном столбце с этим числом. Также выбирается и третье число.
В результате этих действий у вас осталось одно число, его тоже обведите кружочком. Найдите сумму чисел, обведенных кружочком. Эта сумма равна предсказанному числу.
Объяснение. Заметить два числа, находящихся на двух диагонально противоположных углах квадрата. Нужно сложить эти два числа и результат удвоить.