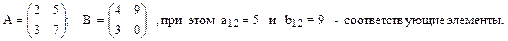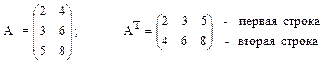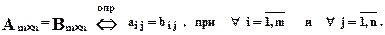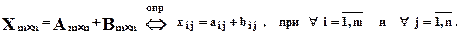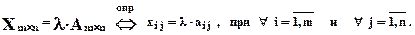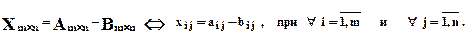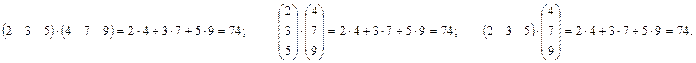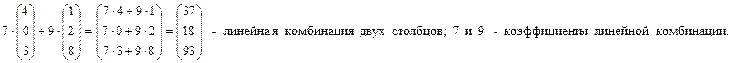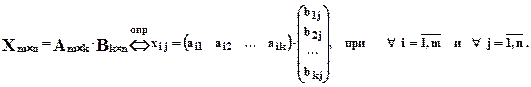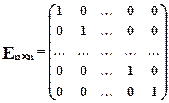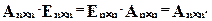что такое главная и побочная диагональ матрицы

Математика для чайников. Матрицы и основные действия над ними

Определение матрицы

Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.

Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.

Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.

Операции сложения и вычитания матриц

Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.

Вычитание выполняется по аналогии, только с противоположным знаком.

Умножение матрицы на число

На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:

Операция умножения матриц

И пример с реальными числами. Умножим матрицы:

Операция транспонирования матрицы

Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:

Определитель матрицы

Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!

Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.

Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.

А если матрица три на три? Тут уже посложнее, но справиться можно.

Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

К счастью, вычислять определители матриц больших размеров на практике приходится редко.

Источник

Побочная диагональ главная диагональ

Санкт-Петербург

Часть IV

ОПОРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ

Э. Н. ОСИПОВА

КАФЕДРА МАТЕМАТИКИ

ТЕХНОЛОГИИ И ДИЗАЙНА

УНИВЕРСИТЕТ

ГОСУДАРСТВЕННЫЙ

САНКТ-ПЕТЕРБУРГСКИЙ

Российской Федерации

(МЕТОДИЧЕСКОЕ ПОСОБИЕ)

1.1. Основные понятия

Матрицей будем называть прямоугольную таблицу чисел, расположенных строками и столбцами; сами числа будем называть элементами матрицы , а число строк и число столбцов образуют размерность матрицы.

Приняты следующие обозначения.

— матрица размерностисодержит 2строки и 3столбца.

— матрица-строка (строка), содержит 1 строку.

— матрица-столбец (столбец), содержит 1столбец.

— матрица содержит mстрок и nстолбцов.

— означает, что i принимает все натуральные значения от 1 до n.

— нулевая матрица размерности .

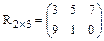
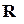
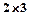
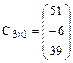
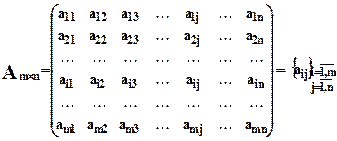
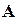
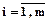
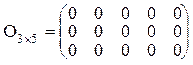
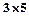
n строк и n столбцов.

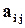
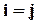
Элементы , у которых образуют ее главную диагональ,

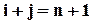
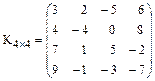
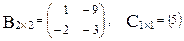
а если , то они образуют побочную диагональ.

— квадратная матрица 4-го порядка.

.

Квадратную матрицу будем называть треугольной, если все элементы, расположенные выше (либо ниже) главной диагонали равны нулю.

.

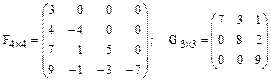
Квадратную матрицу будем называть диагональной, если все ее элементы, нерасположенные на главной диагонали равны нулю.

— диагональная матрица четвертого порядка.

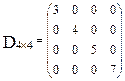
Диагональную матрицу будем называть единичной, если все элементы главнойдиагонали равны 1.

— единичная матрица пятого порядка.

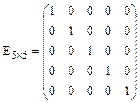
Элементы двух матриц будем называть соответствующими, если они имеют одинаковые индексы. Строки (столбцы) будем называть соответствующими, если они имеют одинаковый номер.

Транспонированием матрицы будем называть операцию замены всех столбцовсоответствующими строками

(всех строк соответствующими столбцами).

Матрицу будем называть симметрической (симметричной), если при транспонировании она не изменяется.

Из определения следует:

— симметрическая матрица может быть только квадратной;

— ее элементы расположены симметрично относительно главной диагонали.

.

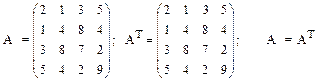
1.2. Действия с матрицами

Произведением матрицы А на скаляр l ( l× А )будем называтьновую матрицу ( Х )той же размерности, каждый элемент которой равен произведению соответствующего элемента данной матрицы на данный скаляр.

Из последних двух определений следует что разность двух матриц может быть найдена следующим образом:

Скалярным произведением двух строк (или двух столбцов, или строки и столбца), имеющих одинаковое количество элементов, будем называть число, равное сумме произведений всех соответствующих элементов.

Линейной комбинацией строк (столбцов) будем называть сумму произведений этих строк (столбцов) на вещественные числа (скаляры).

Сами числа при этом называют коэффициентами этой линейной комбинации.

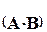
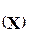
Произведением двух матриц будем называть новую матрицу , у которой каждый элемент х_ijравен скалярному произведению i — ойстроки первого сомножителя на j -й столбец второго сомножителя.

Из определения следуют свойства:

1.2.1. Количество столбцов матрицы-множимого должно быть равно количеству строк матрицы-множителя;

1.2.2. Матрица-произведение имеет столько строк, сколько их у матрицы-множимого и столько столбцов, сколько их у матрицы-множителя.

1.2.3. Умножение матриц не подчиняется переместительному закону.

1.2.4. Квадратные матрицы можно умножать только, если они имеют одинаковый порядок.

1.2.5. Умножение квадратной матрицы на единичную матрицу и слева и справа не изменяет данную матрицу.

;

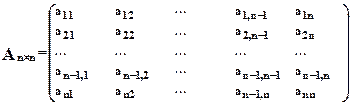
Две квадратные матрицы будем называть взаимно обратными, если их произведение равно единичной матрице.

Источник